Z-test Calculator
Table of contents
This Z-test calculator is a tool that helps you perform a one-sample Z-test on the population's mean . Two forms of this test - a two-tailed Z-test and a one-tailed Z-tests - exist, and can be used depending on your needs. You can also choose whether the calculator should determine the p-value from Z-test or you'd rather use the critical value approach!
Read on to learn more about Z-test in statistics, and, in particular, when to use Z-tests, what is the Z-test formula, and whether to use Z-test vs. t-test. As a bonus, we give some step-by-step examples of how to perform Z-tests!
Or you may also check our t-statistic calculator , where you can learn the concept of another essential statistic. If you are also interested in F-test, check our F-statistic calculator .

What is a Z-test?
A one sample Z-test is one of the most popular location tests. The null hypothesis is that the population mean value is equal to a given number, μ 0 \mu_0 μ 0 :
We perform a two-tailed Z-test if we want to test whether the population mean is not μ 0 \mu_0 μ 0 :
and a one-tailed Z-test if we want to test whether the population mean is less/greater than μ 0 \mu_0 μ 0 :
Let us now discuss the assumptions of a one-sample Z-test.
When do I use Z-tests?
You may use a Z-test if your sample consists of independent data points and:
the data is normally distributed , and you know the population variance ;
the sample is large , and data follows a distribution which has a finite mean and variance. You don't need to know the population variance.
The reason these two possibilities exist is that we want the test statistics that follow the standard normal distribution N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) . In the former case, it is an exact standard normal distribution, while in the latter, it is approximately so, thanks to the central limit theorem.
The question remains, "When is my sample considered large?" Well, there's no universal criterion. In general, the more data points you have, the better the approximation works. Statistics textbooks recommend having no fewer than 50 data points, while 30 is considered the bare minimum.
Z-test formula
Let x 1 , . . . , x n x_1, ..., x_n x 1 , ... , x n be an independent sample following the normal distribution N ( μ , σ 2 ) \mathrm N(\mu, \sigma^2) N ( μ , σ 2 ) , i.e., with a mean equal to μ \mu μ , and variance equal to σ 2 \sigma ^2 σ 2 .
We pose the null hypothesis, H 0 : μ = μ 0 \mathrm H_0 \!\!:\!\! \mu = \mu_0 H 0 : μ = μ 0 .
We define the test statistic, Z , as:
x ˉ \bar x x ˉ is the sample mean, i.e., x ˉ = ( x 1 + . . . + x n ) / n \bar x = (x_1 + ... + x_n) / n x ˉ = ( x 1 + ... + x n ) / n ;
μ 0 \mu_0 μ 0 is the mean postulated in H 0 \mathrm H_0 H 0 ;
n n n is sample size; and
σ \sigma σ is the population standard deviation.
In what follows, the uppercase Z Z Z stands for the test statistic (treated as a random variable), while the lowercase z z z will denote an actual value of Z Z Z , computed for a given sample drawn from N(μ,σ²).
If H 0 \mathrm H_0 H 0 holds, then the sum S n = x 1 + . . . + x n S_n = x_1 + ... + x_n S n = x 1 + ... + x n follows the normal distribution, with mean n μ 0 n \mu_0 n μ 0 and variance n 2 σ n^2 \sigma n 2 σ . As Z Z Z is the standardization (z-score) of S n / n S_n/n S n / n , we can conclude that the test statistic Z Z Z follows the standard normal distribution N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , provided that H 0 \mathrm H_0 H 0 is true. By the way, we have the z-score calculator if you want to focus on this value alone.
If our data does not follow a normal distribution, or if the population standard deviation is unknown (and thus in the formula for Z Z Z we substitute the population standard deviation σ \sigma σ with sample standard deviation), then the test statistics Z Z Z is not necessarily normal. However, if the sample is sufficiently large, then the central limit theorem guarantees that Z Z Z is approximately N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) .
In the sections below, we will explain to you how to use the value of the test statistic, z z z , to make a decision , whether or not you should reject the null hypothesis . Two approaches can be used in order to arrive at that decision: the p-value approach, and critical value approach - and we cover both of them! Which one should you use? In the past, the critical value approach was more popular because it was difficult to calculate p-value from Z-test. However, with help of modern computers, we can do it fairly easily, and with decent precision. In general, you are strongly advised to report the p-value of your tests!
p-value from Z-test
Formally, the p-value is the smallest level of significance at which the null hypothesis could be rejected. More intuitively, p-value answers the questions: provided that I live in a world where the null hypothesis holds, how probable is it that the value of the test statistic will be at least as extreme as the z z z - value I've got for my sample? Hence, a small p-value means that your result is very improbable under the null hypothesis, and so there is strong evidence against the null hypothesis - the smaller the p-value, the stronger the evidence.
To find the p-value, you have to calculate the probability that the test statistic, Z Z Z , is at least as extreme as the value we've actually observed, z z z , provided that the null hypothesis is true. (The probability of an event calculated under the assumption that H 0 \mathrm H_0 H 0 is true will be denoted as P r ( event ∣ H 0 ) \small \mathrm{Pr}(\text{event} | \mathrm{H_0}) Pr ( event ∣ H 0 ) .) It is the alternative hypothesis which determines what more extreme means :
- Two-tailed Z-test: extreme values are those whose absolute value exceeds ∣ z ∣ |z| ∣ z ∣ , so those smaller than − ∣ z ∣ -|z| − ∣ z ∣ or greater than ∣ z ∣ |z| ∣ z ∣ . Therefore, we have:
The symmetry of the normal distribution gives:
- Left-tailed Z-test: extreme values are those smaller than z z z , so
- Right-tailed Z-test: extreme values are those greater than z z z , so
To compute these probabilities, we can use the cumulative distribution function, (cdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , which for a real number, x x x , is defined as:
Also, p-values can be nicely depicted as the area under the probability density function (pdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , due to:
Two-tailed Z-test and one-tailed Z-test
With all the knowledge you've got from the previous section, you're ready to learn about Z-tests.
From the fact that Φ ( − z ) = 1 − Φ ( z ) \Phi(-z) = 1 - \Phi(z) Φ ( − z ) = 1 − Φ ( z ) , we deduce that
The p-value is the area under the probability distribution function (pdf) both to the left of − ∣ z ∣ -|z| − ∣ z ∣ , and to the right of ∣ z ∣ |z| ∣ z ∣ :
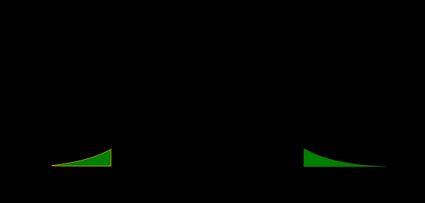
The p-value is the area under the pdf to the left of our z z z :
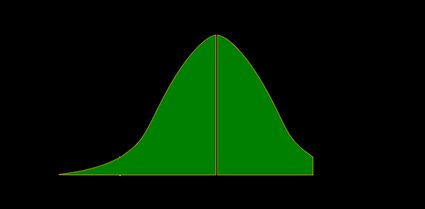
The p-value is the area under the pdf to the right of z z z :

The decision as to whether or not you should reject the null hypothesis can be now made at any significance level, α \alpha α , you desire!
if the p-value is less than, or equal to, α \alpha α , the null hypothesis is rejected at this significance level; and
if the p-value is greater than α \alpha α , then there is not enough evidence to reject the null hypothesis at this significance level.
Z-test critical values & critical regions
The critical value approach involves comparing the value of the test statistic obtained for our sample, z z z , to the so-called critical values . These values constitute the boundaries of regions where the test statistic is highly improbable to lie . Those regions are often referred to as the critical regions , or rejection regions . The decision of whether or not you should reject the null hypothesis is then based on whether or not our z z z belongs to the critical region.
The critical regions depend on a significance level, α \alpha α , of the test, and on the alternative hypothesis. The choice of α \alpha α is arbitrary; in practice, the values of 0.1, 0.05, or 0.01 are most commonly used as α \alpha α .
Once we agree on the value of α \alpha α , we can easily determine the critical regions of the Z-test:
To decide the fate of H 0 \mathrm H_0 H 0 , check whether or not your z z z falls in the critical region:
If yes, then reject H 0 \mathrm H_0 H 0 and accept H 1 \mathrm H_1 H 1 ; and
If no, then there is not enough evidence to reject H 0 \mathrm H_0 H 0 .
As you see, the formulae for the critical values of Z-tests involve the inverse, Φ − 1 \Phi^{-1} Φ − 1 , of the cumulative distribution function (cdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) .
How to use the one-sample Z-test calculator?
Our calculator reduces all the complicated steps:
Choose the alternative hypothesis: two-tailed or left/right-tailed.
In our Z-test calculator, you can decide whether to use the p-value or critical regions approach. In the latter case, set the significance level, α \alpha α .
Enter the value of the test statistic, z z z . If you don't know it, then you can enter some data that will allow us to calculate your z z z for you:
- sample mean x ˉ \bar x x ˉ (If you have raw data, go to the average calculator to determine the mean);
- tested mean μ 0 \mu_0 μ 0 ;
- sample size n n n ; and
- population standard deviation σ \sigma σ (or sample standard deviation if your sample is large).
Results appear immediately below the calculator.
If you want to find z z z based on p-value , please remember that in the case of two-tailed tests there are two possible values of z z z : one positive and one negative, and they are opposite numbers. This Z-test calculator returns the positive value in such a case. In order to find the other possible value of z z z for a given p-value, just take the number opposite to the value of z z z displayed by the calculator.
Z-test examples
To make sure that you've fully understood the essence of Z-test, let's go through some examples:
- A bottle filling machine follows a normal distribution. Its standard deviation, as declared by the manufacturer, is equal to 30 ml. A juice seller claims that the volume poured in each bottle is, on average, one liter, i.e., 1000 ml, but we suspect that in fact the average volume is smaller than that...
Formally, the hypotheses that we set are the following:
H 0 : μ = 1000 ml \mathrm H_0 \! : \mu = 1000 \text{ ml} H 0 : μ = 1000 ml
H 1 : μ < 1000 ml \mathrm H_1 \! : \mu \lt 1000 \text{ ml} H 1 : μ < 1000 ml
We went to a shop and bought a sample of 9 bottles. After carefully measuring the volume of juice in each bottle, we've obtained the following sample (in milliliters):
1020 , 970 , 1000 , 980 , 1010 , 930 , 950 , 980 , 980 \small 1020, 970, 1000, 980, 1010, 930, 950, 980, 980 1020 , 970 , 1000 , 980 , 1010 , 930 , 950 , 980 , 980 .
Sample size: n = 9 n = 9 n = 9 ;
Sample mean: x ˉ = 980 m l \bar x = 980 \ \mathrm{ml} x ˉ = 980 ml ;
Population standard deviation: σ = 30 m l \sigma = 30 \ \mathrm{ml} σ = 30 ml ;
And, therefore, p-value = Φ ( − 2 ) ≈ 0.0228 \text{p-value} = \Phi(-2) \approx 0.0228 p-value = Φ ( − 2 ) ≈ 0.0228 .
As 0.0228 < 0.05 0.0228 \lt 0.05 0.0228 < 0.05 , we conclude that our suspicions aren't groundless; at the most common significance level, 0.05, we would reject the producer's claim, H 0 \mathrm H_0 H 0 , and accept the alternative hypothesis, H 1 \mathrm H_1 H 1 .
We tossed a coin 50 times. We got 20 tails and 30 heads. Is there sufficient evidence to claim that the coin is biased?
Clearly, our data follows Bernoulli distribution, with some success probability p p p and variance σ 2 = p ( 1 − p ) \sigma^2 = p (1-p) σ 2 = p ( 1 − p ) . However, the sample is large, so we can safely perform a Z-test. We adopt the convention that getting tails is a success.
Let us state the null and alternative hypotheses:
H 0 : p = 0.5 \mathrm H_0 \! : p = 0.5 H 0 : p = 0.5 (the coin is fair - the probability of tails is 0.5 0.5 0.5 )
H 1 : p ≠ 0.5 \mathrm H_1 \! : p \ne 0.5 H 1 : p = 0.5 (the coin is biased - the probability of tails differs from 0.5 0.5 0.5 )
In our sample we have 20 successes (denoted by ones) and 30 failures (denoted by zeros), so:
Sample size n = 50 n = 50 n = 50 ;
Sample mean x ˉ = 20 / 50 = 0.4 \bar x = 20/50 = 0.4 x ˉ = 20/50 = 0.4 ;
Population standard deviation is given by σ = 0.5 × 0.5 \sigma = \sqrt{0.5 \times 0.5} σ = 0.5 × 0.5 (because 0.5 0.5 0.5 is the proportion p p p hypothesized in H 0 \mathrm H_0 H 0 ). Hence, σ = 0.5 \sigma = 0.5 σ = 0.5 ;
Since 0.1573 > 0.1 0.1573 \gt 0.1 0.1573 > 0.1 we don't have enough evidence to reject the claim that the coin is fair , even at such a large significance level as 0.1 0.1 0.1 . In that case, you may safely toss it to your Witcher or use the coin flip probability calculator to find your chances of getting, e.g., 10 heads in a row (which are extremely low!).
What is the difference between Z-test vs t-test?
We use a t-test for testing the population mean of a normally distributed dataset which had an unknown population standard deviation . We get this by replacing the population standard deviation in the Z-test statistic formula by the sample standard deviation, which means that this new test statistic follows (provided that H₀ holds) the t-Student distribution with n-1 degrees of freedom instead of N(0,1) .
When should I use t-test over the Z-test?
For large samples, the t-Student distribution with n degrees of freedom approaches the N(0,1). Hence, as long as there are a sufficient number of data points (at least 30), it does not really matter whether you use the Z-test or the t-test, since the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test instead of Z-test .
How do I calculate the Z test statistic?
To calculate the Z test statistic:
- Compute the arithmetic mean of your sample .
- From this mean subtract the mean postulated in null hypothesis .
- Multiply by the square root of size sample .
- Divide by the population standard deviation .
- That's it, you've just computed the Z test statistic!
Here, we perform a Z-test for population mean μ. Null hypothesis H₀: μ = μ₀.
Alternative hypothesis H₁
Significance level α
The probability that we reject the true hypothesis H₀ (type I error).
Hypothesis Testing Calculator
| $\text{Test Statistic: }$ | | = | | | |
| $\text{Degrees of Freedom: } $ | $df$ | = | |
| $ \text{Level of Significance: } $ | $\alpha$ | = | |
Type II Error
| $H_o$: | $\mu$ | | |
| $H_a$: | $\mu$ | ≠ | $\mu_0$ |
| $\text{Level of Significance: }$ | $\alpha$ | = | |
The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.
| $\sigma$ Known | $\sigma$ Unknown |
| Test Statistic | $ z = \dfrac{\bar{x}-\mu_0}{\sigma/\sqrt{{\color{Black} n}}} $ | $ t = \dfrac{\bar{x}-\mu_0}{s/\sqrt{n}} $ |
Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.
| Lower Tail Test | Upper Tail Test | Two-Tailed Test |
| $H_0 \colon \mu \geq \mu_0$ | $H_0 \colon \mu \leq \mu_0$ | $H_0 \colon \mu = \mu_0$ |
| $H_a \colon \mu | $H_a \colon \mu \neq \mu_0$ |
In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.
To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.
In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.
To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.
| Lower Tail Test | Upper Tail Test | Two-Tailed Test |
| If $z \leq -z_\alpha$, reject $H_0$. | If $z \geq z_\alpha$, reject $H_0$. | If $z \leq -z_{\alpha/2}$ or $z \geq z_{\alpha/2}$, reject $H_0$. |
| If $t \leq -t_\alpha$, reject $H_0$. | If $t \geq t_\alpha$, reject $H_0$. | If $t \leq -t_{\alpha/2}$ or $t \geq t_{\alpha/2}$, reject $H_0$. |
When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.
| | Condition | |
| | $H_0$ True | $H_a$ True |
| Conclusion | Accept $H_0$ | Correct | Type II Error |
| Reject $H_0$ | Type I Error | Correct |
Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.
Z-Test Calculator
| | |
| Sample size, n | |
| Population mean, μ | |
| Population standard deviation, σ | |
| Alternative hypothesis H : | | | Sample 1 | | Sample mean, x̅ | | | Sample size, n | | | Population standard deviation, σ | | | Sample 2 | | Sample mean, x̅ | | | Sample size, n | | | Population standard deviation, σ | | | | | Population mean difference, d | | | Alternative hypothesis H : | -μ ≠d -μ <d -μ >d | This Z-test calculator computes data for both one-sample and two-sample Z-tests. It also provides a diagram to show the position of the Z-score and the acceptance/rejection regions. When making a two-sample Z-test calculation, the population mean difference, d, represents the difference between the population means of sample one and sample two, which is μ 1 -μ 2 . To use this calculator, simply select the type of calculation from the tab, enter the values, and click the 'Calculate' button. The Z-test is a statistical procedure used to determine whether there is a significant difference between means, either between a sample mean and a known population mean (one-sample Z-test) or between the means of two independent samples (two-sample Z-test). It assumes that the data is normally distributed and is particularly useful when the sample sizes are large (>30) and the population standard deviations are known. When analyzing data to make informed decisions, statistical hypothesis tests are indispensable tools used to determine if evidence exists to reject a prevailing assumption or theory, known as the null hypothesis. The Z-test is one of these tests. One-Sample Z-TestThe one-sample Z-test is used when you want to compare the mean of a single sample to a known population mean to see if there is a significant difference. This is particularly common in quality control and other scenarios where the standard deviation of the population is known. - Null Hypothesis (H 0 ): The sample mean is equal to the population mean (x̅=μ).
- Alternative Hypothesis (H 1 ): The sample mean is not equal to the population mean (x̅≠μ). This can also be one-tailed (x̅>μ or x̅<μ) depending on the direction of interest.
The formula for the Z-statistic in a one-sample Z-test is: | Z = | | x̅ - μ | | - x̅ is the sample mean
- μ is the population mean
- σ is the population standard deviation
- n is the sample size
Example: Suppose a school administrator knows the national average score for a standardized test is 500 with a standard deviation of 50. A sample of 100 students from a new teaching program scores an average of 520. To determine if this program significantly differs from the national average: | Z = | | 520 - 500 | | This Z-value would then be compared against a critical value from the Z-distribution table typically at a 0.05 significance level. The critical value for a 0.05 significance level is approximately ±1.96. The Z-value of 4 is greater than 1.96. Therefore, the null hypothesis is rejected and the score of this program is considered significantly different from the national average at the 0.05 significance level. Two-Sample Z-TestThe two-sample Z-test (or independent samples Z-test) compares the means from two independent groups to determine if there is a statistically significant difference between them. - Null Hypothesis (H 0 ): The two population means have a difference of d (μ 1 -μ 2 =d). If d is 0, the null hypothesis states that the two population means are equal (μ 1 =μ 2 ).
- Alternative Hypothesis (H 1 ): The difference between two population means is not d (μ 1 -μ 2 ≠d), which can also be directional (μ 1 -μ 2 >d or μ 1 -μ 2 <d). If d is 0, the alternative hypothesis becomes μ 1 ≠μ 2 , or μ 1 >μ 2 or μ 1 <μ 2 if it is directional.
The formula for calculating the Z-statistic in a two-sample Z-test is: | Z = | | (x̅ - x̅ ) - (μ - μ ) | | | √ | - x̅ 1 and x̅ 2 are the sample means of groups 1 and 2, respectively
- μ 1 and μ 2 are the population means, with μ 1 - μ 2 = d. d is often hypothesized to be zero under the null hypothesis.
- σ 1 and σ 2 are the population standard deviations
- n 1 and n 2 are the sample sizes of the two groups
Example: Consider two groups of employees from different branches of a company undergoing training. Group A has 50 employees with an average score of 80 and a standard deviation of 10, and Group B has 50 employees with an average score of 75 and a standard deviation of 12. To test if there's a significant difference: | Z = | | (80 - 75) - 0 | | | √ | This Z-value is then compared to the critical Z-values to assess significance. The critical value of a 0.05 significance level is around ±1.95. The Z-value of 2.26 is more than 1.95. Therefore, the two group has significant difference at 0.05 significance level. Significance LevelThe significance level (α) is a critical concept in hypothesis testing. It represents the probability threshold below which the null hypothesis will be rejected. Common levels are 0.05 (5%) or 0.01 (1%). The choice of α affects the Z-critical value, which is used to determine whether to reject the null hypothesis based on the computed Z-score. - Critical Value: This is a point on the Z-distribution that the test statistic must exceed to reject the null hypothesis. For instance, at a 5% significance level in a two-tailed test, the critical values are approximately ±1.96. The significance level (probability) and critical value (Z-score) can be converted with each other the Z-distribution table or use our Z/P converter .
Using the above examples, if the computed Z-scores exceed the respective critical values, the null hypotheses in each case would be rejected, indicating a statistically significant difference as per the alternative hypotheses. These examples demonstrate how the Z-test is applied in different scenarios to test hypotheses concerning population means. - Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim Making statistics intuitive Z Test: Uses, Formula & ExamplesBy Jim Frost Leave a Comment What is a Z Test?Use a Z test when you need to compare group means. Use the 1-sample analysis to determine whether a population mean is different from a hypothesized value. Or use the 2-sample version to determine whether two population means differ. A Z test is a form of inferential statistics . It uses samples to draw conclusions about populations. For example, use Z tests to assess the following: - One sample : Do students in an honors program have an average IQ score different than a hypothesized value of 100?
- Two sample : Do two IQ boosting programs have different mean scores?
In this post, learn about when to use a Z test vs T test. Then we’ll review the Z test’s hypotheses, assumptions, interpretation, and formula. Finally, we’ll use the formula in a worked example. Related post : Difference between Descriptive and Inferential Statistics Z test vs T testZ tests and t tests are similar. They both assess the means of one or two groups, have similar assumptions, and allow you to draw the same conclusions about population means. However, there is one critical difference. Z tests require you to know the population standard deviation, while t tests use a sample estimate of the standard deviation. Learn more about Population Parameters vs. Sample Statistics . In practice, analysts rarely use Z tests because it’s rare that they’ll know the population standard deviation. It’s even rarer that they’ll know it and yet need to assess an unknown population mean! A Z test is often the first hypothesis test students learn because its results are easier to calculate by hand and it builds on the standard normal distribution that they probably already understand. Additionally, students don’t need to know about the degrees of freedom . Z and T test results converge as the sample size approaches infinity. Indeed, for sample sizes greater than 30, the differences between the two analyses become small. William Sealy Gosset developed the t test specifically to account for the additional uncertainty associated with smaller samples. Conversely, Z tests are too sensitive to mean differences in smaller samples and can produce statistically significant results incorrectly (i.e., false positives). When to use a T Test vs Z TestLet’s put a button on it. When you know the population standard deviation, use a Z test. When you have a sample estimate of the standard deviation, which will be the vast majority of the time, the best statistical practice is to use a t test regardless of the sample size. However, the difference between the two analyses becomes trivial when the sample size exceeds 30. Learn more about a T-Test Overview: How to Use & Examples and How T-Tests Work . Z Test HypothesesThis analysis uses sample data to evaluate hypotheses that refer to population means (µ). The hypotheses depend on whether you’re assessing one or two samples. One-Sample Z Test Hypotheses- Null hypothesis (H 0 ): The population mean equals a hypothesized value (µ = µ 0 ).
- Alternative hypothesis (H A ): The population mean DOES NOT equal a hypothesized value (µ ≠ µ 0 ).
When the p-value is less or equal to your significance level (e.g., 0.05), reject the null hypothesis. The difference between your sample mean and the hypothesized value is statistically significant. Your sample data support the notion that the population mean does not equal the hypothesized value. Related posts : Null Hypothesis: Definition, Rejecting & Examples and Understanding Significance Levels Two-Sample Z Test Hypotheses- Null hypothesis (H 0 ): Two population means are equal (µ 1 = µ 2 ).
- Alternative hypothesis (H A ): Two population means are not equal (µ 1 ≠ µ 2 ).
Again, when the p-value is less than or equal to your significance level, reject the null hypothesis. The difference between the two means is statistically significant. Your sample data support the idea that the two population means are different. These hypotheses are for two-sided analyses. You can use one-sided, directional hypotheses instead. Learn more in my post, One-Tailed and Two-Tailed Hypothesis Tests Explained . Related posts : How to Interpret P Values and Statistical Significance Z Test AssumptionsFor reliable results, your data should satisfy the following assumptions: You have a random sampleDrawing a random sample from your target population helps ensure that the sample represents the population. Representative samples are crucial for accurately inferring population properties. The Z test results won’t be valid if your data do not reflect the population. Related posts : Random Sampling and Representative Samples Continuous dataZ tests require continuous data . Continuous variables can assume any numeric value, and the scale can be divided meaningfully into smaller increments, such as fractional and decimal values. For example, weight, height, and temperature are continuous. Other analyses can assess additional data types. For more information, read Comparing Hypothesis Tests for Continuous, Binary, and Count Data . Your sample data follow a normal distribution, or you have a large sample sizeAll Z tests assume your data follow a normal distribution . However, due to the central limit theorem, you can ignore this assumption when your sample is large enough. The following sample size guidelines indicate when normality becomes less of a concern: - One-Sample : 20 or more observations.
- Two-Sample : At least 15 in each group.
Related posts : Central Limit Theorem and Skewed Distributions Independent samplesFor the two-sample analysis, the groups must contain different sets of items. This analysis compares two distinct samples. Related post : Independent and Dependent Samples Population standard deviation is knownAs I mention in the Z test vs T test section, use a Z test when you know the population standard deviation. However, when n > 30, the difference between the analyses becomes trivial. Related post : Standard Deviations Z Test FormulaThese Z test formulas allow you to calculate the test statistic. Use the Z statistic to determine statistical significance by comparing it to the appropriate critical values and use it to find p-values. The correct formula depends on whether you’re performing a one- or two-sample analysis. Both formulas require sample means (x̅) and sample sizes (n) from your sample. Additionally, you specify the population standard deviation (σ) or variance (σ 2 ), which does not come from your sample. I present a worked example using the Z test formula at the end of this post. Learn more about Z-Scores and Test Statistics . One Sample Z Test Formula The one sample Z test formula is a ratio. The numerator is the difference between your sample mean and a hypothesized value for the population mean (µ 0 ). This value is often a strawman argument that you hope to disprove. The denominator is the standard error of the mean. It represents the uncertainty in how well the sample mean estimates the population mean. Learn more about the Standard Error of the Mean . Two Sample Z Test Formula The two sample Z test formula is also a ratio. The numerator is the difference between your two sample means. The denominator calculates the pooled standard error of the mean by combining both samples. In this Z test formula, enter the population variances (σ 2 ) for each sample.  Z Test Critical ValuesAs I mentioned in the Z vs T test section, a Z test does not use degrees of freedom. It evaluates Z-scores in the context of the standard normal distribution. Unlike the t-distribution , the standard normal distribution doesn’t change shape as the sample size changes. Consequently, the critical values don’t change with the sample size. To find the critical value for a Z test, you need to know the significance level and whether it is one- or two-tailed. | | | | | 0.01 | Two-Tailed | ±2.576 | | 0.01 | Left Tail | –2.326 | | 0.01 | Right Tail | +2.326 | | 0.05 | Two-Tailed | ±1.960 | | 0.05 | Left Tail | +1.650 | | 0.05 | Right Tail | –1.650 | Learn more about Critical Values: Definition, Finding & Calculator . Z Test Worked ExampleLet’s close this post by calculating the results for a Z test by hand! Suppose we randomly sampled subjects from an honors program. We want to determine whether their mean IQ score differs from the general population. The general population’s IQ scores are defined as having a mean of 100 and a standard deviation of 15. We’ll determine whether the difference between our sample mean and the hypothesized population mean of 100 is statistically significant. Specifically, we’ll use a two-tailed analysis with a significance level of 0.05. Looking at the table above, you’ll see that this Z test has critical values of ± 1.960. Our results are statistically significant if our Z statistic is below –1.960 or above +1.960. The hypotheses are the following: - Null (H 0 ): µ = 100
- Alternative (H A ): µ ≠ 100
Entering Our Results into the FormulaHere are the values from our study that we need to enter into the Z test formula: - IQ score sample mean (x̅): 107
- Sample size (n): 25
- Hypothesized population mean (µ 0 ): 100
- Population standard deviation (σ): 15
 The Z-score is 2.333. This value is greater than the critical value of 1.960, making the results statistically significant. Below is a graphical representation of our Z test results showing how the Z statistic falls within the critical region.  We can reject the null and conclude that the mean IQ score for the population of honors students does not equal 100. Based on the sample mean of 107, we know their mean IQ score is higher. Now let’s find the p-value. We could use technology to do that, such as an online calculator. However, let’s go old school and use a Z table. To find the p-value that corresponds to a Z-score from a two-tailed analysis, we need to find the negative value of our Z-score (even when it’s positive) and double it. In the truncated Z-table below, I highlight the cell corresponding to a Z-score of -2.33.  The cell value of 0.00990 represents the area or probability to the left of the Z-score -2.33. We need to double it to include the area > +2.33 to obtain the p-value for a two-tailed analysis. P-value = 0.00990 * 2 = 0.0198 That p-value is an approximation because it uses a Z-score of 2.33 rather than 2.333. Using an online calculator, the p-value for our Z test is a more precise 0.0196. This p-value is less than our significance level of 0.05, which reconfirms the statistically significant results. See my full Z-table , which explains how to use it to solve other types of problems. Share this: Reader InteractionsComments and questions cancel reply. - Skip to main content
- Skip to primary sidebar
- Skip to footer
Savvy Calculator Savvy Calculator is a free online tool of calculations. One Sample Z-Test CalculatorAbout one sample z-test calculator (formula). A One Sample Z-Test is a statistical test used to determine whether the mean of a single sample differs significantly from a known population mean or a hypothesized mean. This test is commonly used in hypothesis testing when you have a single set of data points and want to determine if it’s representative of a larger population or if there’s a significant difference between the sample and the population. Here’s the formula for a One Sample Z-Test: Z = (X̄ – μ) / (σ / √(n)) - Z is the Z-statistic.
- X̄ (pronounced as “X-bar”) is the sample mean.
- μ (pronounced as “mu”) is the population mean (the known mean or the hypothesized mean).
- σ (pronounced as “sigma”) is the population standard deviation (if known).
- n is the sample size.
The steps to perform a One Sample Z-Test are as follows: - H0: The sample mean is equal to the population mean (μ).
- Ha: The sample mean is not equal to the population mean (μ), indicating a two-tailed test. Alternatively, you can use a one-tailed test if you have a specific direction in mind (greater than or less than).
- Collect your sample data and calculate the sample mean (X̄) and, if possible, the population standard deviation (σ).
- Determine the significance level (α), which represents the probability of making a Type I error (rejecting the null hypothesis when it is true). Common choices for α include 0.05 and 0.01.
- Calculate the Z-statistic using the formula mentioned above.
- Compare the calculated Z-statistic to the critical Z-value(s) from the standard normal distribution table or use a statistical calculator. The critical value(s) correspond to your chosen significance level (α) and the type of test (two-tailed or one-tailed).
- If |Z| > critical value: Reject the null hypothesis (H0) in favor of the alternative hypothesis (Ha).
- If |Z| ≤ critical value: Fail to reject the null hypothesis (H0).
- Draw a conclusion based on your decision and report the results.
This test helps you determine whether the observed difference between your sample mean and the population mean is statistically significant or if it could have occurred due to random sampling variation. Keep in mind that for practical purposes, it’s often recommended to use statistical software or calculators to perform One Sample Z-Tests because they can handle the calculations and critical value lookup efficiently. - Privacy Policy
- Terms and Conditions
  One Sample Z-Test CalculatorOne Sample z-test is used to check whether the population mean is statistically significantly different from a hypothesized value. It is used when the population standard deviation is known. In the calculation below you have two options - either to enter raw data or you can enter summary information which is required to calculate one sample z-test. Enter Raw Data Enter Summary Data Step by Step Calculation $$ s_{\bar{x}} = \frac{\sigma}{\sqrt{n}} $$ \(\mu_{0}\) : Hypothesized value \(\bar{x}\) : Sample mean \(n\) : Sample size \(\sigma_{}\) : Population standard deviation \(s_{\bar{x}}\) : Estimated standard error of the mean - Data must be normally distributed
- One-sample z-test assumes that the standard deviation of the population is already known.
- Sample must be picked randomly from population
- Data must be continuous
 - Calculators
- Descriptive Statistics
- Merchandise
- Which Statistics Test?
Z Score Calculator for 2 Population ProportionsThis is a simple z score calculator that calculates the value of z (and associated p value) for two population proportions. Further Information The z score test for two population proportions is used when you want to know whether two populations or groups (e.g., males and females; theists and atheists) differ significantly on some single (categorical) characteristic - for example, whether they are vegetarians. Requirements - A random sample of each of the population groups to be compared.
- Categorial data
Null Hypothesis H0: p1 - p2 = 0, where p1 is the proportion from the first population and p2 the proportion from the second. As above, the null hypothesis tends to be that there is no difference between the two population proportions; or, more formally, that the difference is zero (so, for example, that there is no difference between the proportion of males who are vegetarian and the proportion of females who are vegetarian).  Z-Test CalculatorsZ-tests are crucial statistical procedures to test for claims about population parameters using the normal distribution. Z-tests, as all parametric tests, require certain distributional assumptions to be met. As with anything in Statistics, we need to look for signs to assess whether it is likely not that the distributional assumptions are met. Typically, a Z-test will require the underlying distribution to be normally distributed, but such assumption can be typically be relaxed when the sample size is large enough, by virtue of the Central Limit Theorem. Applications of Z-testsWe can use for one population or two population means provided that the population standard deviations are known. Also, we can use a z-test to test for claims about a population proportion. Also, via the Central Limit Theorem (CLT), the z-test can be used as an approximation by many statistical procedures (parametric and non-parametric). In this page you will all the Z-tests we have available. Check the list below:  Z-test for One Population Mean Z-test: One Population Proportion Z-test for two Means, with Known Population Standard Deviations Z-test for Two ProportionsRelated posts:.  In case you have any suggestion, or if you would like to report a broken solver/calculator, please do not hesitate to contact us . log in to your accountReset password. Input 2 ProportionsFormula and output, when do you use z-test two independent sample means. | Soil type 1 | Soil type 2 | | n1 = 30 | n2 = 35 | | mean1 = 1.65 | mean2 = 1.43 | | s1 = 0.26 | s2 = 0.22 | |
When performing a Z-test on two independent samples you want to sum the variances of the means and then take the square root to find the standard deviation of variance sum. In this example you are given the standard deviations for each sample thus you need to take the square of the standar deviations to find the variances: - Variance sample 1 = 0.26^2 = 0.0676 - Variance sample 2 = 0.22^2 = 0.0484 Now when you have the variances you use the formula for Z-test two independent samples or you can use the calculator provided. The Z-value is 3.648 which is above the critical value of 2.5758 (two tailed test), thus there is a significant difference between the soils. Two Sample Z-Test CalculatorEnter sample data. | | | |
Z-test claculator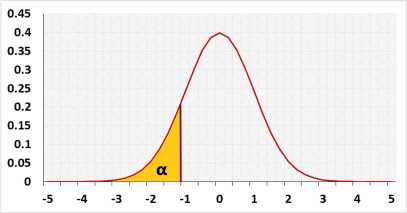 Assumptions| ,σ - The standard deviations of both populations are known (either σ =σ or ϭ ≠ϭ ) |
Required Sample Data| , x - Sample average of group1 and group2 | | ,n - Sample size of group1 and group2 |
Calculators Two sample z test calculatorWelcome to our comprehensive Two Sample Z Test Calculator! This tool helps you perform a two-sample Z test for hypothesis testing quickly and accurately. our calculator simplifies the process of determining p-values, critical value, test statistics, degree of freedom, decision and Conclusion. Whether you're a student, researcher, or data analyst, our calculator streamlines the process by offering detailed steps and results for your investigation. Enter below values for sample 1 : Enter below values for sample 2: Related Calculators :- List of all calculator
- P-value calculator
- Critical value Calculator
- One sample t test calculator
What is a Two Sample Z Test?The Two Sample Z Test is a statistical tool for determining whether there is a significant difference between the means of two independent samples. This test is used when the population variances are known and the sample size is big (usually \( \mathrm{ n > 30} \)). It is widely used in fields including economics, biology, engineering, and social sciences. Key Features of Our Two Sample Z Test CalculatorEasy Data Entry: Enter your sample data directly or provide summary statistics such as sample means and standard deviations. Hypothesis Testing: Use both the p-value and critical value approaches to hypothesis testing. Detailed Results: Get detailed results, including test statistics, p-values, critical values, and a clear conclusion on the hypothesis. Customizable Rounding: Set the desired level of precision for test statistics, p-values, and critical values. How to Use the Two Sample Z Test CalculatorSelect Data Type: Choose whether to enter raw data or summary statistics. Enter Sample Data: Give the appropriate figures for sample sizes, means, and standard deviations. Set Hypotheses: Define your null and alternative hypotheses. Significance Level: Input your chosen significance level ( \( \alpha \) ). Calculate : Click the "Calculate" button to perform the test. Suppose you want to compare the average heights of two different species of plants. You collect a sample of \(50\) plants from species A and \(45\) plants from species B. The sample mean height for species A is \(30\) cm with a population standard deviation of \(5\) cm, while the sample mean height for species B is \(28\) cm with a population standard deviation of \(6\) cm. Using our Two Sample Z Test Calculator, you can determine if the difference in average height is statistically significant. Why Choose Our Two Sample Z Test Calculator?User-Friendly Interface: The intuitive design makes it simple to enter data and evaluate results. Accurate Calculations: Reliable algorithms ensure that your statistical tests yield exact results. Educational Value: Detailed explanations help users understand the steps and results of the test, making it an excellent learning tool. Frequently Asked Questions (FAQ)Q: When should I use a Two Sample Z Test? A: Use a Two Sample Z Test when you need to compare the means of two independent samples and the population variances are known or assumed to be equal. Q: What is the difference between a Z Test and a T Test? A: A Z Test is used for large sample sizes (n > 30) with known variances, while a T Test is used for smaller sample sizes or when population variances are unknown. Q: How do I interpret the p-value? A: The p-value indicates the probability of obtaining the observed results if the null hypothesis is true. A p-value less than the significance level \((\alpha)\) suggests rejecting the null hypothesis.  Two Sample Z-Test Calculatorz = -1.608761 p-value (one-tailed) = 0.060963 p-value (two-tailed) = 0.121926 Featured Posts Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations. One Reply to “Two Sample Z-Test Calculator”Have you seen my cat garfield I lost him and he loves lasagna Leave a Reply Cancel replyYour email address will not be published. Required fields are marked * Join the Statology CommunitySign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox! By subscribing you accept Statology's Privacy Policy.  |
|
|
|
|
|
|
|
| |





















IMAGES
VIDEO
COMMENTS
This Z-test calculator is a tool that helps you perform a one-sample Z-test on the population's mean. Two forms of this test - a two-tailed Z-test and a one-tailed Z-tests - exist, and can be used depending on your needs. ... The critical regions depend on a significance level, α \alpha α, of the test, and on the alternative hypothesis.
Hypothesis Testing Calculator. The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is ...
This Z-test calculator computes data for both one-sample and two-sample Z-tests. It also provides a diagram to show the position of the Z-score and the acceptance/rejection regions. ... (1%). The choice of α affects the Z-critical value, which is used to determine whether to reject the null hypothesis based on the computed Z-score. Critical ...
Calculation Example: There are six steps you would follow in hypothesis testing: Formulate the null and alternative hypotheses in three different ways: H 0: θ = θ 0 v e r s u s H 1: θ ≠ θ 0. H 0: θ ≤ θ 0 v e r s u s H 1: θ > θ 0. H 0: θ ≥ θ 0 v e r s u s H 1: θ < θ 0.
A one sample z-test is used to test whether or not the mean of a population is equal to some value when the population standard deviation is known. To perform a one sample z-test, simply fill in the information below and then click the "Calculate" button. Enter raw data Enter summary data.
z-test calculator. Natural Language; Math Input; Extended Keyboard Examples Upload Random. Computational Inputs: » hypothesized mean ... right‐tailed test. Compute. Input interpretation. Input values. Null hypothesis. Alternative hypothesis. Test statistic. p ‐value. Sampling distribution of test statistic under the null hypothesis. Power ...
A Z test is often the first hypothesis test students learn because its results are easier to calculate by hand and it builds on the standard normal distribution that they probably already understand. ... Using an online calculator, the p-value for our Z test is a more precise 0.0196. This p-value is less than our significance level of 0.05 ...
Calculate: Click the "Calculate" button to see the test statistic, p-value, and other relevant results. Interpreting the Results The results of the one-sample Z test will indicate whether you should reject the null hypothesis.
This calculator conducts a Z-test for one population mean µ, with known population standard deviation σ. Please select the null and alternative hypotheses, type the hypothesized mean, the significance level, the sample mean, the population standard deviation, and the sample size, and the results of the z-test will be displayed for you.
Single Sample Z Score Calculator. This tool calculates the z -score of the mean of a single sample. It can be used to make a judgement about whether the sample differs significantly on some axis from the population from which it was originally drawn. By default, this tool works on the assumption that you already know the mean value of your ...
The steps to perform a One Sample Z-Test are as follows: Formulate the null hypothesis (H0) and the alternative hypothesis (H1 or Ha). H0: The sample mean is equal to the population mean (μ). Ha: The sample mean is not equal to the population mean (μ), indicating a two-tailed test. Alternatively, you can use a one-tailed test if you have a ...
Please enter the value of p above, and then press "Calculate Z from P". Additional Z Statistic Calculators. If you're interested in using the z statistic for hypothesis testing, then we have a couple of other calculators that might help you. Z-Test Calculator for a Single Sample Z-Test Calculator for 2 Population Proportions
The below is the solved examples for Z-statistic calculation by using standard deviation & without using standard deviation. Z-test calculator, formulas & example work with steps to estimate z-statistic (Z0), critical value of normal distribution (Ze) & test of hypothesis (H0) for large sample mean, proportion & two means or proportions ...
Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Z-Hypothesis Testing (stats) Save Copy ... Enter M_0, the value of the null hypothesis and click on the tab below corresponding to the proper form of the alternative hypothesis. Or ...
Z test online. Target: To check if the assumed μ 0 is statistically correct, based on a sample average. You know the standard deviation from previous researches. Example1: A farmer calculated last year the average of the apples' weight in his apple orchard μ 0 equals 17 kg, based on the entire population. The current year he checked a small ...
Instructions: This calculator conducts a Z-test for two population means ( \mu_1 μ1 and \mu_2 μ2 ), with known population standard deviations ( \sigma_1 σ1 and \sigma_2 σ2 ). Please select the null and alternative hypotheses, type the significance level, the sample means, the population standard deviations, the sample sizes, and the results ...
One Sample Z-Test Calculator. One Sample z-test is used to check whether the population mean is statistically significantly different from a hypothesized value. It is used when the population standard deviation is known. In the calculation below you have two options - either to enter raw data or you can enter summary information which is ...
This is a simple z score calculator that calculates the value of z (and associated p value) for two population proportions. Further Information. The z score test for two population proportions is used when you want to know whether two populations or groups (e.g., males and females; theists and atheists) differ significantly on some single ...
Z-test for Two Proportions. Instructions: This calculator conducts a Z-test for two population proportions ( (p_1) and (p_2)), Please select the null and alternative hypotheses, type the significance level, the sample sizes, the number of favorable cases (or the sample ... In case you have any suggestion, or if you would like to report a broken ...
In this example you are given the standard deviations for each sample thus you need to take the square of the standar deviations to find the variances: - Variance sample 1 = 0.26^2 = 0.0676. - Variance sample 2 = 0.22^2 = 0.0484. Now when you have the variances you use the formula for Z-test two independent samples or you can use the calculator ...
Z-test claculator. Target: To check if the difference between the average (mean) of two groups is significant. Example1: A man of average height is expected to be 10cm taller than a woman of average height (d=10) Example2: The average weight of an apple grown in field 1 is expected to be equal in weight to the average apple grown in field 2 (d ...
How to Use the Two Sample Z Test Calculator. Select Data Type: Choose whether to enter raw data or summary statistics. Enter Sample Data: Give the appropriate figures for sample sizes, means, and standard deviations. Set Hypotheses: Define your null and alternative hypotheses. Significance Level: Input your chosen significance level ( α ).
Two Sample Z-Test Calculator. by Zach Bobbitt June 30, 2022. A two sample z-test is used to test whether or not the means of two populations are equal when the population standard deviations are known. To perform a two sample z-test, simply fill in the information below and then click the "Calculate" button. Enter raw data Enter summary data.