case study on gauss law

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Question for Class 12 Physics Chapter 1 Electric Charges and Fields

Last modified on: 2 years ago
Reading Time: 19 Minutes

There is Case Study Questions in class 12 Physics in session 2020-21. The first two questions in the board exam question paper will be based on Case Study and Assertion & Reason. Case Study Questions will have 5 MCQs out of which students will have to attempt any 4 questions. Here are the questions based on case study.

Case Study Question 1:

Electric field strength is proportional to the density of lines of force i.e., electric field strength at a point is proportional to the number of lines of force cutting a unit area element placed normal to the field at that point. As illustrated in given figure, the electric field at P is stronger than at Q.

(i) Electric lines of force about a positive point charge are (a) radially outwards (b) circular clockwise (c) radially inwards (d) parallel straight lines

(ii) Which of the following is false for electric lines of force? (a) They always start from positive charge and terminate on negative charges. (b) They are always perpendicular to the surface of a charged conductor. (c) They always form closed loops. (d) They are parallel and equally spaced in a region of uniform electric field.

(iii) Which one of the following patterns of electric line of force is not possible in field due to stationary charges?

(iv) Electric field lines are curved (a) in the field of a single positive or negative charge (b) in the field of two equal and opposite charges. (c) in the field of two like charges. (d) both (b) and (c)

(v) The figure below shows the electric field lines due to two positive charges. The magnitudes E A , E B and E C of the electric fields at point A, B and C respectively are related as

(a) E A >E B >E C (b) E B >E A >E C (c) E A =E B >E C (d) E A >E B =E C

Case Study Question 2:

Smallest charge that can exist in nature is the charge of an electron. During friction it is only the transfer of electron which makes the body charged. Hence net charge on any body is an integral multiple of charge of an electron (1.6 x 10 -19 C) i.e., q=±ne where r= 1, 2, 3, 4 …. Hence no body can have a charge represented as 1.8e, 2.7e, 2e/5, etc. Recently, it has been discovered that elementary particles such as protons or neutrons are elemental units called quarks.

(i) Which of the following properties is not satisfied by an electric charge? (a) Total charge conservation. (b) Quantization of charge. (c) Two types of charge. (d) Circular line of force.

(ii) Which one of the following charges is possible? (a) 5.8 x 10 -18 C (b) 3.2 x 10 -18 C (c) 4.5 x 10 -19 C (d) 8.6 x 10 -19 C

(iii) If a charge on a body is 1 nC, then how many electrons are present on the body? (a) 6.25 x 10 27 (b) 1.6 x 10 19 (c) 6.25 X 10 28 (d) 6.25 X 10 9

(iv) If a body gives out 10 9 electrons every second, how much time is required to get a total charge of 1 from it? (a) 190.19 years (b) 150.12 years (c) 198.19 years (d) 188.21 years

(v) A polythene piece rubbed with wool is found to have a negative charge of 3.2 x 10 -7 C. Calculate the number of electrons transferred. (a) 2 x 10 12 (b) 3 x 10 12 (c) 2 x 10 14 (d) 3 x 10 14

Case Study Question 3:

When electric dipole is placed in uniform electric field, its two charges experience equal and opposite forces, which cancel each other and hence net force on electric dipole in uniform electric field is zero. However these forces are not collinear, so they give rise to some torque on the dipole. Since net force on electric dipole in uniform electric field is zero, so no work is done in moving the electric dipole in uniform electric field. However some work is done in rotating the dipole against the torque acting on it.

(i) The dipole moment of a dipole in a uniform external field Ē is B. Then the torque τ acting on the dipole is (a) τ=p x E (b) τ = P. Ē (c) τ = 2(p + Ē) (d) τ = (P + E)

(ii) An electric dipole consists of two opposite charges, each of magnitude 1.0 μC separated by a distance of 2.0 cm. The dipole is placed in an external field of 10 5 NC -1 . The maximum torque on the dipole is (a) 0.2 x 10 -3 Nm (b) 1x 10 -3 Nm (c) 2 x 10 -3 Nm (d) 4x 10 -3 Nm

(iii) Torque on a dipole in uniform electric field is minimum when θ is equal to (a) 0° (b) 90° (c) 180° (d) Both (a) and (c)

(iv) When an electric dipole is held at an angle in a uniform electric field, the net force F and torque τ on the dipole are (a) F= 0, τ = 0 (b) F≠0, τ≠0 (c) F=0, τ ≠ 0 (d) F≠0, τ=0

(v) An electric dipole of moment p is placed in an electric field of intensity E. The dipole acquires a position such that the axis of the dipole makes an angle with the direction of the field. Assuming that potential energy of the dipole to be zero when 0 = 90°, the torque and the potential energy of the dipole will respectively be (a) pEsinθ, -pEcosθ (b) pEsinθ, -2pEcosθ (c) pEsinθ, 2pEcosθ (d) pEcosθ, – pEsinθ

Case Study Question 4:

A charge is a property associated with the matter due to which it experiences and produces an electric and magnetic field. Charges are scalar in nature and they add up like real number. Also, the total charge of an isolated system is always conserved. When the objects rub against each other charges acquired by them must be equal and opposite.

(i) The cause of a charging is: (a) the actual transfer of protons. (b) the actual transfer of electrons. (c) the actual transfer of neutrons. (d) none the above

(ii) Pick the correct statement. (a) The glass rod gives protons to silk when they are rubbed against each other. (b) The glass rod gives electrons to silk when they are rubbed against each other. (c) The glass rod gains protons from silk when they are rubbed against each other. (d) The glass rod gains electrons when they are rubbed against each other.

(iii) If two electrons are each 1.5 × 10 –10 m from a proton, the magnitude of the net electric force they will exert on the proton is (a) 1.97 × 10 –8 N (b) 2.73 × 10 –8 N (c) 3.83 × 10 –8 N (d) 4.63 × 10 –8 N

(iv) A charge is a property associated with the matter due to which it produces and experiences: (a) electric effects only (b) magnetic effects only (c) both electric and magnetic effects (d) none of these.

(v) The cause of quantization of electric charges is: (a) Transfer of an integral number of neutrons. (b) Transfer of an integral number of protons. (c) Transfer of an integral number of electrons. (d) None of the above.

Case Study Question 5:

Surface Charge Density. Surface charge density is defined as the charge per unit surface area the surface (Arial) charge symmetric distribution and follow Gauss law of electro statics mathematical term of surface charge density σ=ΔQ/ΔS

Two large thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite sign (± s). Having magnitude 8.8 × 10 –12 cm –2 as shown here. The intensity of electrified at a point is E =σ/ε 0 and flux is Φ=E.ΔS, where ΔS = 1 m 2 (unit arial plate)

(i) E in the outer region (I) of the first (A) plate is (a) 1.7 × 10 –22 N/C (b) 1.1 × 10 –12 V/m (c) Zero (d) Insufficient data

(ii) E in the outer region (III) of the second plate (B) is (a) 1 N/C (b) 0.1 V/m (c) 0.5 N/C (d) zero

(iii) E between (II) the plate is (a) 1 N/C (b) 0.1 V/m (c) 0.5 N/C (d) None of these

(iv) The ratio of E from left side of plate A at distance 1 cm and 2 m respectively is (a) 1 : 2 (b) 10 : 2 (c) 1 : 1 (d) 20 : 1

(v) In order to estimate the electric field due to a thin finite plane metal plate the Gaussian surface considered is (a) Spherical (b) Linear (c) Cylindrical (d) Cybic

Download CBSE Books

Exam Special Series:

Sample Question Paper for CBSE Class 10 Science (for 2024)
Sample Question Paper for CBSE Class 10 Maths (for 2024)
CBSE Most Repeated Questions for Class 10 Science Board Exams
CBSE Important Diagram Based Questions Class 10 Physics Board Exams
CBSE Important Numericals Class 10 Physics Board Exams
CBSE Practical Based Questions for Class 10 Science Board Exams
CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
Sample Question Papers for CBSE Class 12 Physics (for 2024)
Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
Sample Question Papers for CBSE Class 12 Maths (for 2024)
Sample Question Papers for CBSE Class 12 Biology (for 2024)
CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
Master Organic Conversions CBSE Class 12 Chemistry Board Exams
CBSE Important Numericals Class 12 Physics Board Exams
CBSE Important Definitions Class 12 Physics Board Exams
CBSE Important Laws & Principles Class 12 Physics Board Exams
10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
ICSE Important Functions and Locations Based Questions Class 10 Biology
ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

6 thoughts on “ Case Study Question for Class 12 Physics Chapter 1 Electric Charges and Fields ”

Only 1 case study question from every chapter with no answer

Answers will be uploaded soon….more questions will be added. Stay tuned.

Answers uploaded.

Where the solutions of this content?

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

LOADING PAGE...

Dear Reader,

There are several reasons you might be seeing this page. In order to read the online edition of The Feynman Lectures on Physics , javascript must be supported by your browser and enabled. If you have have visited this website previously it's possible you may have a mixture of incompatible files (.js, .css, and .html) in your browser cache. If you use an ad blocker it may be preventing our pages from downloading necessary resources. So, please try the following: make sure javascript is enabled, clear your browser cache (at least of files from feynmanlectures.caltech.edu), turn off your browser extensions, and open this page:

If it does not open, or only shows you this message again, then please let us know:

which browser you are using (including version #)
which operating system you are using (including version #)

This type of problem is rare, and there's a good chance it can be fixed if we have some clues about the cause. So, if you can, after enabling javascript, clearing the cache and disabling extensions, please open your browser's javascript console, load the page above, and if this generates any messages (particularly errors or warnings) on the console, then please make a copy (text or screenshot) of those messages and send them with the above-listed information to the email address given below.

By sending us information you will be helping not only yourself, but others who may be having similar problems accessing the online edition of The Feynman Lectures on Physics . Your time and consideration are greatly appreciated.

Best regards, Mike Gottlieb [email protected] Editor, The Feynman Lectures on Physics New Millennium Edition

5 Application of Gauss’ Law

5–1 Electrostatics is Gauss’ law plus …

There are two laws of electrostatics: that the flux of the electric field from a volume is proportional to the charge inside—Gauss’ law, and that the circulation of the electric field is zero—$\FLPE$ is a gradient. From these two laws, all the predictions of electrostatics follow. But to say these things mathematically is one thing; to use them easily, and with a certain amount of ingenuity, is another. In this chapter we will work through a number of calculations which can be made with Gauss’ law directly. We will prove theorems and describe some effects, particularly in conductors, that can be understood very easily from Gauss’ law. Gauss’ law by itself cannot give the solution of any problem because the other law must be obeyed too. So when we use Gauss’ law for the solution of particular problems, we will have to add something to it. We will have to presuppose, for instance, some idea of how the field looks—based, for example, on arguments of symmetry. Or we may have to introduce specifically the idea that the field is the gradient of a potential.

5–2 Equilibrium in an electrostatic field

Consider first the following question: When can a point charge be in stable mechanical equilibrium in the electric field of other charges? As an example, imagine three negative charges at the corners of an equilateral triangle in a horizontal plane. Would a positive charge placed at the center of the triangle remain there? (It will be simpler if we ignore gravity for the moment, although including it would not change the results.) The force on the positive charge is zero, but is the equilibrium stable? Would the charge return to the equilibrium position if displaced slightly? The answer is no.

There are no points of stable equilibrium in any electrostatic field—except right on top of another charge. Using Gauss’ law, it is easy to see why. First, for a charge to be in equilibrium at any particular point $P_0$, the field must be zero. Second, if the equilibrium is to be a stable one, we require that if we move the charge away from $P_0$ in any direction, there should be a restoring force directed opposite to the displacement. The electric field at all nearby points must be pointing inward—toward the point $P_0$. But that is in violation of Gauss’ law if there is no charge at $P_0$, as we can easily see.

Consider a tiny imaginary surface that encloses $P_0$, as in Fig. 5–1 . If the electric field everywhere in the vicinity is pointed toward $P_0$, the surface integral of the normal component is certainly not zero. For the case shown in the figure, the flux through the surface must be a negative number. But Gauss’ law says that the flux of electric field through any surface is proportional to the total charge inside. If there is no charge at $P_0$, the field we have imagined violates Gauss’ law. It is impossible to balance a positive charge in empty space—at a point where there is not some negative charge. A positive charge can be in equilibrium if it is in the middle of a distributed negative charge. Of course, the negative charge distribution would have to be held in place by other than electrical forces!

Our result has been obtained for a point charge. Does the same conclusion hold for a complicated arrangement of charges held together in fixed relative positions—with rods, for example? We consider the question for two equal charges fixed on a rod. Is it possible that this combination can be in equilibrium in some electrostatic field? The answer is again no. The total force on the rod cannot be restoring for displacements in every direction.

Call $\FLPF$ the total force on the rod in any position—$\FLPF$ is then a vector field. Following the argument used above, we conclude that at a position of stable equilibrium, the divergence of $\FLPF$ must be a negative number. But the total force on the rod is the first charge times the field at its position, plus the second charge times the field at its position: \begin{equation} \label{Eq:II:5:1} \FLPF=q_1\FLPE_1+q_2\FLPE_2. \end{equation} The divergence of $\FLPF$ is given by \begin{equation*} \FLPdiv{\FLPF}=q_1(\FLPdiv{\FLPE_1})+q_2(\FLPdiv{\FLPE_2}). \end{equation*} If each of the two charges $q_1$ and $q_2$ is in free space, both $\FLPdiv{\FLPE_1}$ and $\FLPdiv{\FLPE_2}$ are zero, and $\FLPdiv{\FLPF}$ is zero—not negative, as would be required for equilibrium. You can see that an extension of the argument shows that no rigid combination of any number of charges can have a position of stable equilibrium in an electrostatic field in free space.

Now we have not shown that equilibrium is forbidden if there are pivots or other mechanical constraints. As an example, consider a hollow tube in which a charge can move back and forth freely, but not sideways. Now it is very easy to devise an electric field that points inward at both ends of the tube if it is allowed that the field may point laterally outward near the center of the tube. We simply place positive charges at each end of the tube, as in Fig. 5–2 . There can now be an equilibrium point even though the divergence of $\FLPE$ is zero. The charge, of course, would not be in stable equilibrium for sideways motion were it not for “nonelectrical” forces from the tube walls.

5–3 Equilibrium with conductors

There is no stable spot in the field of a system of fixed charges. What about a system of charged conductors? Can a system of charged conductors produce a field that will have a stable equilibrium point for a point charge? (We mean at a point other than on a conductor, of course.) You know that conductors have the property that charges can move freely around in them. Perhaps when the point charge is displaced slightly, the other charges on the conductors will move in a way that will give a restoring force to the point charge? The answer is still no—although the proof we have just given doesn’t show it. The proof for this case is more difficult, and we will only indicate how it goes.

First, we note that when charges redistribute themselves on the conductors, they can only do so if their motion decreases their total potential energy. (Some energy is lost to heat as they move in the conductor.) Now we have already shown that if the charges producing a field are stationary , there is, near any zero point $P_0$ in the field, some direction for which moving a point charge away from $P_0$ will decrease the energy of the system (since the force is away from $P_0$). Any readjustment of the charges on the conductors can only lower the potential energy still more, so (by the principle of virtual work) their motion will only increase the force in that particular direction away from $P_0$, and not reverse it.

Our conclusions do not mean that it is not possible to balance a charge by electrical forces. It is possible if one is willing to control the locations or the sizes of the supporting charges with suitable devices. You know that a rod standing on its point in a gravitational field is unstable, but this does not prove that it cannot be balanced on the end of a finger. Similarly, a charge can be held in one spot by electric fields if they are variable . But not with a passive—that is, a static —system.

5–4 Stability of atoms

If charges cannot be held stably in position, it is surely not proper to imagine matter to be made up of static point charges (electrons and protons) governed only by the laws of electrostatics. Such a static configuration is impossible; it would collapse!

It was once suggested that the positive charge of an atom could be distributed uniformly in a sphere, and the negative charges, the electrons, could be at rest inside the positive charge, as shown in Fig. 5–3 . This was the first atomic model, proposed by Thomson. But Rutherford concluded from the experiment of Geiger and Marsden that the positive charges were very much concentrated, in what he called the nucleus. Thomson’s static model had to be abandoned. Rutherford and Bohr then suggested that the equilibrium might be dynamic, with the electrons revolving in orbits, as shown in Fig. 5–4 . The electrons would be kept from falling in toward the nucleus by their orbital motion. We already know at least one difficulty with this picture. With such motion, the electrons would be accelerating (because of the circular motion) and would, therefore, be radiating energy. They would lose the kinetic energy required to stay in orbit, and would spiral in toward the nucleus. Again unstable!

The stability of the atoms is now explained in terms of quantum mechanics. The electrostatic forces pull the electron as close to the nucleus as possible, but the electron is compelled to stay spread out in space over a distance given by the uncertainty principle. If it were confined in too small a space, it would have a great uncertainty in momentum. But that means that it would have a high expected energy—which it would use to escape from the electrical attraction. The net result is an electrical equilibrium not too different from the idea of Thomson—only it is the negative charge that is spread out (because the mass of the electron is so much smaller than the mass of the proton).

5–5 The field of a line charge

Gauss’ law can be used to solve a number of electrostatic field problems involving a special symmetry—usually spherical, cylindrical, or planar symmetry. In the remainder of this chapter we will apply Gauss’ law to a few such problems. The ease with which these problems can be solved may give the misleading impression that the method is very powerful, and that one should be able to go on to many other problems. It is unfortunately not so. One soon exhausts the list of problems that can be solved easily with Gauss’ law. In later chapters we will develop more powerful methods for investigating electrostatic fields.

As our first example, we consider a system with cylindrical symmetry. Suppose that we have a very long, uniformly charged rod. By this we mean that electric charges are distributed uniformly along an indefinitely long straight line, with the charge $\lambda$ per unit length. We wish to know the electric field. The problem can, of course, be solved by integrating the contribution to the field from every part of the line. We are going to do it without integrating, by using Gauss’ law and some guesswork. First, we surmise that the electric field will be directed radially outward from the line. Any axial component from charges on one side would be accompanied by an equal axial component from charges on the other side. The result could only be a radial field. It also seems reasonable that the field should have the same magnitude at all points equidistant from the line. This is obvious. (It may not be easy to prove, but it is true if space is symmetric—as we believe it is.)

We can use Gauss’ law in the following way. We consider an imaginary surface in the shape of a cylinder coaxial with the line, as shown in Fig. 5–5 . According to Gauss’ law, the total flux of $\FLPE$ from this surface is equal to the charge inside divided by $\epsO$. Since the field is assumed to be normal to the surface, the normal component is the magnitude of the field. Let’s call it $E$. Also, let the radius of the cylinder be $r$, and its length be taken as one unit, for convenience. The flux through the cylindrical surface is equal to $E$ times the area of the surface, which is $2\pi r$. The flux through the two end faces is zero because the electric field is tangential to them. The total charge inside our surface is just $\lambda$, because the length of the line inside is one unit. Gauss’ law then gives \begin{gather} E\cdot2\pi r=\lambda/\epsO,\notag\\[1ex] \label{Eq:II:5:2} E=\frac{\lambda}{2\pi\epsO r}. \end{gather} The electric field of a line charge depends inversely on the first power of the distance from the line.

5–6 A sheet of charge; two sheets

As another example, we will calculate the field from a uniform plane sheet of charge. Suppose that the sheet is infinite in extent and that the charge per unit area is $\sigma$. We are going to take another guess. Considerations of symmetry lead us to believe that the field direction is everywhere normal to the plane, and if we have no field from any other charges in the world , the fields must be the same (in magnitude) on each side. This time we choose for our Gaussian surface a rectangular box that cuts through the sheet, as shown in Fig. 5–6 . The two faces parallel to the sheet will have equal areas, say $A$. The field is normal to these two faces, and parallel to the other four. The total flux is $E$ times the area of the first face, plus $E$ times the area of the opposite face—with no contribution from the other four faces. The total charge enclosed in the box is $\sigma A$. Equating the flux to the charge inside, we have \begin{equation} EA+EA=\frac{\sigma A}{\epsO},\notag \end{equation} from which \begin{equation} \label{Eq:II:5:3} E=\frac{\sigma}{2\epsO}, \end{equation} a simple but important result.

You may remember that the same result was obtained in an earlier chapter by an integration over the entire surface. Gauss’ law gives us the answer, in this instance, much more quickly (although it is not as generally applicable as the earlier method).

We emphasize that this result applies only to the field due to the charges on the sheet. If there are other charges in the neighborhood, the total field near the sheet would be the sum of ( 5.3 ) and the field of the other charges. Gauss’ law would then tell us only that \begin{equation} \label{Eq:II:5:4} E_1+E_2=\frac{\sigma}{\epsO}, \end{equation} where $E_1$ and $E_2$ are the fields directed outward on each side of the sheet.

The problem of two parallel sheets with equal and opposite charge densities, $+\sigma$ and $-\sigma$, is equally simple if we assume again that the outside world is quite symmetric. Either by superposing two solutions for a single sheet or by constructing a Gaussian box that includes both sheets, it is easily seen that the field is zero outside of the two sheets (Fig. 5–7 a). By considering a box that includes only one surface or the other, as in (b) or (c) of the figure, it can be seen that the field between the sheets must be twice what it is for a single sheet. The result is \begin{alignat}{2} \label{Eq:II:5:5} &E\,(\text{between the sheets})&\,=&\,\sigma/\epsO,\\[2ex] \label{Eq:II:5:6} &E\,(\text{outside}) &\,=&\,0. \end{alignat}

5–7 A sphere of charge; a spherical shell

We have already (in Chapter 4 ) used Gauss’ law to find the field outside a uniformly charged spherical region. The same method can also give us the field at points inside the sphere. For example, the computation can be used to obtain a good approximation to the field inside an atomic nucleus. In spite of the fact that the protons in a nucleus repel each other, they are, because of the strong nuclear forces, spread nearly uniformly throughout the body of the nucleus.

Suppose that we have a sphere of radius $R$ filled uniformly with charge. Let $\rho$ be the charge per unit volume. Again using arguments of symmetry, we assume the field to be radial and equal in magnitude at all points at the same distance from the center. To find the field at the distance $r$ from the center, we take a spherical Gaussian surface of radius $r$ ($r<R$), as shown in Fig. 5–8 . The flux out of this surface is \begin{equation*} 4\pi r^2E. \end{equation*} The charge inside our Gaussian surface is the volume inside times $\rho$, or \begin{equation*} \tfrac{4}{3}\pi r^3\rho. \end{equation*} Using Gauss’ law, it follows that the magnitude of the field is given by \begin{equation} \label{Eq:II:5:7} E=\frac{\rho r}{3\epsO}\quad(r<R). \end{equation} You can see that this formula gives the proper result for $r=R$. The electric field is proportional to the radius and is directed radially outward.

The arguments we have just given for a uniformly charged sphere can be applied also to a thin spherical shell of charge. Assuming that the field is everywhere radial and is spherically symmetric, one gets immediately from Gauss’ law that the field outside the shell is like that of a point charge, while the field everywhere inside the shell is zero. (A Gaussian surface inside the shell will contain no charge.)

5–8 Is the field of a point charge exactly $\boldsymbol{1/r^2}$?

If we look in a little more detail at how the field inside the shell gets to be zero, we can see more clearly why it is that Gauss’ law is true only because the Coulomb force depends exactly on the square of the distance. Consider any point $P$ inside a uniform spherical shell of charge. Imagine a small cone whose apex is at $P$ and which extends to the surface of the sphere, where it cuts out a small surface area $\Delta a_1$, as in Fig. 5–9 . An exactly symmetric cone diverging from the opposite side of $P$ would cut out the surface area $\Delta a_2$. If the distances from $P$ to these two elements of area are $r_1$ and $r_2$, the areas are in the ratio \begin{equation*} \frac{\Delta a_2}{\Delta a_1}=\frac{r_2^2}{r_1^2}. \end{equation*} (You can show this by geometry for any point $P$ inside the sphere.)

If the surface of the sphere is uniformly charged, the charge $\Delta q$ on each of the elements of area is proportional to the area, so \begin{equation*} \frac{\Delta q_2}{\Delta q_1}=\frac{\Delta a_2}{\Delta a_1}. \end{equation*} Coulomb’s law then says that the magnitudes of the fields produced at $P$ by these two surface elements are in the ratio \begin{equation*} \frac{E_2}{E_1}=\frac{\Delta q_2/r_2^2}{\Delta q_1/r_1^2}=1. \end{equation*} The fields cancel exactly. Since all parts of the surface can be paired off in the same way, the total field at $P$ is zero. But you can see that it would not be so if the exponent of $r$ in Coulomb’s law were not exactly two.

The validity of Gauss’ law depends upon the inverse square law of Coulomb. If the force law were not exactly the inverse square, it would not be true that the field inside a uniformly charged sphere would be exactly zero. For instance, if the force varied more rapidly, like, say, the inverse cube of $r$, that portion of the surface which is nearer to an interior point would produce a field which is larger than that which is farther away, resulting in a radial inward field for a positive surface charge. These conclusions suggest an elegant way of finding out whether the inverse square law is precisely correct. We need only determine whether or not the field inside of a uniformly charged spherical shell is precisely zero.

It is lucky that such a method exists. It is usually difficult to measure a physical quantity to high precision—a one percent result may not be too difficult, but how would one go about measuring, say, Coulomb’s law to an accuracy of one part in a billion? It is almost certainly not possible with the best available techniques to measure the force between two charged objects with such an accuracy. But by determining only that the electric fields inside a charged sphere are smaller than some value we can make a highly accurate measurement of the correctness of Gauss’ law, and hence of the inverse square dependence of Coulomb’s law. What one does, in effect, is compare the force law to an ideal inverse square. Such comparisons of things that are equal, or nearly so, are usually the bases of the most precise physical measurements.

How shall we observe the field inside a charged sphere? One way is to try to charge an object by touching it to the inside of a spherical conductor. You know that if we touch a small metal ball to a charged object and then touch it to an electrometer the meter will become charged and the pointer will move from zero (Fig. 5–10 a). The ball picks up charge because there are electric fields outside the charged sphere that cause charges to run onto (or off) the little ball. If you do the same experiment by touching the little ball to the inside of the charged sphere, you find that no charge is carried to the electrometer. With such an experiment you can easily show that the field inside is, at most, a few percent of the field outside, and that Gauss’ law is at least approximately correct.

It appears that Benjamin Franklin was the first to notice that the field inside a conducting shell is zero. The result seemed strange to him. When he reported his observation to Priestley, the latter suggested that it might be connected with an inverse square law, since it was known that a spherical shell of matter produced no gravitational field inside. But Coulomb didn’t measure the inverse square dependence until 18 years later, and Gauss’ law came even later still.

Gauss’ law has been checked carefully by putting an electrometer inside a large sphere and observing whether any deflections occur when the sphere is charged to a high voltage. A null result is always obtained. Knowing the geometry of the apparatus and the sensitivity of the meter, it is possible to compute the minimum field that would be observed. From this number it is possible to place an upper limit on the deviation of the exponent from two. If we write that the electrostatic force depends on $r^{-2+\epsilon}$, we can place an upper bound on $\epsilon$. By this method Maxwell determined that $\epsilon$ was less than $1/10{,}000$. The experiment was repeated and improved upon in 1936 by Plimpton and Lawton. They found that Coulomb’s exponent differs from two by less than one part in a billion.

Now that brings up an interesting question: How accurate do we know this Coulomb law to be in various circumstances? The experiments we just described measure the dependence of the field on distance for distances of some tens of centimeters. But what about the distances inside an atom—in the hydrogen atom, for instance, where we believe the electron is attracted to the nucleus by the same inverse square law? It is true that quantum mechanics must be used for the mechanical part of the behavior of the electron, but the force is the usual electrostatic one. In the formulation of the problem, the potential energy of an electron must be known as a function of distance from the nucleus, and Coulomb’s law gives a potential which varies inversely with the first power of the distance. How accurately is the exponent known for such small distances? As a result of very careful measurements in 1947 by Lamb and Retherford on the relative positions of the energy levels of hydrogen, we know that the exponent is correct again to one part in a billion on the atomic scale—that is, at distances of the order of one angstrom ($10^{-8}$ centimeter).

The accuracy of the Lamb-Retherford measurement was possible again because of a physical “accident.” Two of the states of a hydrogen atom are expected to have almost identical energies only if the potential varies exactly as $1/r$. A measurement was made of the very slight difference in energies by finding the frequency $\omega$ of the photons that are emitted or absorbed in the transition from one state to the other, using for the energy difference $\Delta E=\hbar\omega$. Computations showed that $\Delta E$ would have been noticeably different from what was observed if the exponent in the force law $1/r^2$ differed from $2$ by as much as one part in a billion.

Is the same exponent correct at still shorter distances? From measurements in nuclear physics it is found that there are electrostatic forces at typical nuclear distances—at about $10^{-13}$ centimeter—and that they still vary approximately as the inverse square. We shall look at some of the evidence in a later chapter. Coulomb’s law is, we know, still valid, at least to some extent, at distances of the order of $10^{-13}$ centimeter.

How about $10^{-14}$ centimeter? This range can be investigated by bombarding protons with very energetic electrons and observing how they are scattered. Results to date seem to indicate that the law fails at these distances. The electrical force seems to be about $10$ times too weak at distances less than $10^{-14}$ centimeter. Now there are two possible explanations. One is that the Coulomb law does not work at such small distances; the other is that our objects, the electrons and protons, are not point charges. Perhaps either the electron or proton, or both, is some kind of a smear. Most physicists prefer to think that the charge of the proton is smeared. We know that protons interact strongly with mesons. This implies that a proton will, from time to time, exist as a neutron with a $\pi^+$ meson around it. Such a configuration would act—on the average—like a little sphere of positive charge. We know that the field from a sphere of charge does not vary as $1/r^2$ all the way into the center. It is quite likely that the proton charge is smeared, but the theory of pions is still quite incomplete, so it may also be that Coulomb’s law fails at very small distances. The question is still open.

One more point: The inverse square law is valid at distances like one meter and also at $10^{-10}$ m; but is the coefficient $1/4\pi\epsO$ the same? The answer is yes; at least to an accuracy of $15$ parts in a million.

We go back now to an important matter that we slighted when we spoke of the experimental verification of Gauss’ law. You may have wondered how the experiment of Maxwell or of Plimpton and Lawton could give such an accuracy unless the spherical conductor they used was a perfect sphere. An accuracy of one part in a billion is really something to achieve, and you might well ask whether they could make a sphere which was that precise. There are certain to be slight irregularities in any real sphere and if there are irregularities, will they not produce fields inside? We wish to show now that it is not necessary to have a perfect sphere. It is possible, in fact, to show that there is no field inside a closed conducting shell of any shape. In other words, the experiments depended on $1/r^2$, but had nothing to do with the surface being a sphere (except that with a sphere it is easier to calculate what the fields would be if Coulomb had been wrong), so we take up that subject now. To show this, it is necessary to know some of the properties of electrical conductors.

5–9 The fields of a conductor

An electrical conductor is a solid that contains many “free” electrons. The electrons can move around freely in the material, but cannot leave the surface. In a metal there are so many free electrons that any electric field will set large numbers of them into motion. Either the current of electrons so set up must be continually kept moving by external sources of energy, or the motion of the electrons will cease as they discharge the sources producing the initial field. In “electrostatic” situations, we do not consider continuous sources of current (they will be considered later when we study magnetostatics), so the electrons move only until they have arranged themselves to produce zero electric field everywhere inside the conductor. (This usually happens in a small fraction of a second.) If there were any field left, this field would urge still more electrons to move; the only electrostatic solution is that the field is everywhere zero inside.

Now consider the interior of a charged conducting object. (By “interior” we mean in the metal itself.) Since the metal is a conductor, the interior field must be zero, and so the gradient of the potential $\phi$ is zero. That means that $\phi$ does not vary from point to point. Every conductor is an equipotential region , and its surface is an equipotential surface. Since in a conducting material the electric field is everywhere zero, the divergence of $\FLPE$ is zero, and by Gauss’ law the charge density in the interior of the conductor must be zero.

If there can be no charges in a conductor, how can it ever be charged? What do we mean when we say a conductor is “charged”? Where are the charges? The answer is that they reside at the surface of the conductor, where there are strong forces to keep them from leaving—they are not completely “free.” When we study solid-state physics, we shall find that the excess charge of any conductor is on the average within one or two atomic layers of the surface. For our present purposes, it is accurate enough to say that if any charge is put on, or in , a conductor it all accumulates on the surface; there is no charge in the interior of a conductor.

We note also that the electric field just outside the surface of a conductor must be normal to the surface. There can be no tangential component. If there were a tangential component, the electrons would move along the surface; there are no forces preventing that. Saying it another way: we know that the electric field lines must always go at right angles to an equipotential surface.

We can also, using Gauss’ law, relate the field strength just outside a conductor to the local density of the charge at the surface. For a Gaussian surface, we take a small cylindrical box half inside and half outside the surface, like the one shown in Fig. 5–11 . There is a contribution to the total flux of $\FLPE$ only from the side of the box outside the conductor. The field just outside the surface of a conductor is then Outside a conductor: \begin{equation} \label{Eq:II:5:8} E=\frac{\sigma}{\epsO}, \end{equation} where $\sigma$ is the local surface charge density.

Why does a sheet of charge on a conductor produce a different field than just a sheet of charge? In other words, why is ( 5.8 ) twice as large as ( 5.3 )? The reason, of course, is that we have not said for the conductor that there are no “other” charges around. There must, in fact, be some to make $\FLPE=\FLPzero$ in the conductor. The charges in the immediate neighborhood of a point $P$ on the surface do, in fact, give a field $E_{\text{local}}=\sigma_{\text{local}}/2\epsO$ both inside and outside the surface. But all the rest of the charges on the conductor “conspire” to produce an additional field at the point $P$ equal in magnitude to $E_{\text{local}}$. The total field inside goes to zero and the field outside to $2E_{\text{local}}=\sigma/\epsO$.

5–10 The field in a cavity of a conductor

We return now to the problem of the hollow container—a conductor with a cavity. There is no field in the metal , but what about in the cavity ? We shall show that if the cavity is empty then there are no fields in it, no matter what the shape of the conductor or the cavity—say for the one in Fig. 5–12 . Consider a Gaussian surface, like $S$ in Fig. 5–12 , that encloses the cavity but stays everywhere in the conducting material. Everywhere on $S$ the field is zero, so there is no flux through $S$ and the total charge inside $S$ is zero. For a spherical shell, one could then argue from symmetry that there could be no charge inside. But, in general, we can only say that there are equal amounts of positive and negative charge on the inner surface of the conductor. There could be a positive surface charge on one part and a negative one somewhere else, as indicated in Fig. 5–12 . Such a thing cannot be ruled out by Gauss’ law.

What really happens, of course, is that any equal and opposite charges on the inner surface would slide around to meet each other, cancelling out completely. We can show that they must cancel completely by using the law that the circulation of $\FLPE$ is always zero (electrostatics). Suppose there were charges on some parts of the inner surface. We know that there would have to be an equal number of opposite charges somewhere else. Now any lines of $\FLPE$ would have to start on the positive charges and end on the negative charges (since we are considering only the case that there are no free charges in the cavity). Now imagine a loop $\Gamma$ that crosses the cavity along a line of force from some positive charge to some negative charge, and returns to its starting point via the conductor (as in Fig. 5–12 ). The integral along such a line of force from the positive to the negative charges would not be zero. The integral through the metal is zero, since $\FLPE=\FLPzero$. So we would have \begin{equation*} \oint\FLPE\cdot d\FLPs\neq0??? \end{equation*} But the line integral of $\FLPE$ around any closed loop in an electrostatic field is always zero. So there can be no fields inside the empty cavity, nor any charges on the inside surface.

You should notice carefully one important qualification we have made. We have always said “inside an empty ” cavity. If some charges are placed at some fixed locations in the cavity—as on an insulator or on a small conductor insulated from the main one—then there can be fields in the cavity. But then that is not an “empty” cavity.

We have shown that if a cavity is completely enclosed by a conductor, no static distribution of charges outside can ever produce any fields inside. This explains the principle of “shielding” electrical equipment by placing it in a metal can. The same arguments can be used to show that no static distribution of charges inside a closed grounded conductor can produce any fields outside . Shielding works both ways! In electrostatics—but not in varying fields—the fields on the two sides of a closed grounded conducting shell are completely independent.

Now you see why it was possible to check Coulomb’s law to such a great precision. The shape of the hollow shell used doesn’t matter. It doesn’t need to be spherical; it could be square! If Gauss’ law is exact, the field inside is always zero. Now you also understand why it is safe to sit inside the high-voltage terminal of a million-volt Van de Graaff generator, without worrying about getting a shock—because of Gauss’ law.

IIT JEE Study Material

Gauss Law - Applications, Gauss Theorem Formula

Gauss law states that the total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity. The electric flux in an area is defined as the electric field multiplied by the area of the surface projected in a plane and perpendicular to the field.

Download Complete Chapter Notes of Electric Charges and Fields Download Now

JEE Main 2021 LIVE Physics Paper Solutions 24 Feb Shift-1 Memory-based

Table of Content:

What is gauss law.

Gauss Theorem
Applications
Frequently Asked Questions

According to Gauss law, the total flux linked with a closed surface is 1/ε 0 times the charge enclosed by the closed surface.

For example, a point charge q is placed inside a cube of the edge ‘a’. Now, as per Gauss law , the flux through each face of the cube is q/6ε 0 .

The electric field is the basic concept of knowing about electricity. Generally, the electric field of the surface is calculated by applying Coulomb’s law , but to calculate the electric field distribution in a closed surface, we need to understand the concept of Gauss law. It explains the electric charge enclosed in a closed surface or the electric charge present in the enclosed closed surface.

Gauss Law Formula

As per the Gauss theorem, the total charge enclosed in a closed surface is proportional to the total flux enclosed by the surface. Therefore, if ϕ is total flux and ϵ 0 is electric constant, the total electric charge Q enclosed by the surface is

The Gauss law formula is expressed by

Q = Total charge within the given surface

ε 0 = The electric constant

⇒ Also Read: Equipotential Surface

The Gauss Theorem

The net flux through a closed surface is directly proportional to the net charge in the volume enclosed by the closed surface.

Φ = → E.d → A = q net /ε 0

In simple words, the Gauss theorem relates the ‘flow’ of electric field lines (flux) to the charges within the enclosed surface. If no charges are enclosed by a surface, then the net electric flux remains zero.

This means that the number of electric field lines entering the surface equals the field lines leaving the surface.

The Gauss theorem statement also gives an important corollary:

The electric flux from any closed surface is only due to the sources (positive charges) and sinks (negative charges) of the electric fields enclosed by the surface. Any charges outside the surface do not contribute to the electric flux. Also, only electric charges can act as sources or sinks of electric fields. Changing magnetic fields , for example, cannot act as sources or sinks of electric fields.

Gauss Law in Magnetism

The net flux for the surface on the left is non-zero as it encloses a net charge. The net flux for the surface on the right is zero since it does not enclose any charge.

⇒ Note: The Gauss law is only a restatement of Coulomb’s law. If you apply the Gauss theorem to a point charge enclosed by a sphere, you will get back Coulomb’s law easily.

Applications of Gauss Law

1. In the case of a charged ring of radius R on its axis at a distance x from the centre of the ring. $\begin{array}{l}E = \frac{1}{4\pi {{\in }_{0}}}\frac{qx}{{{\left( {{R}^{2}}+{{x}^{2}} \right)}^{3/2}}}\end{array} $ . At the centre, x = 0 and E = 0.

2. In the case of an infinite line of charge, at a distance, ‘r’. E = (1/4 × πrε 0 ) (2π/r) = λ/2πrε 0 . Where λ is the linear charge density.

3. The intensity of the electric field near a plane sheet of charge is E = σ/2ε 0 K, where σ = Surface charge density.

4. The intensity of the electric field near a plane-charged conductor E = σ/Kε 0 in a medium of dielectric constant K. If the dielectric medium is air, then E air = σ/ε 0 .

5 . The field between two parallel plates of a condenser is E = σ/ε 0 , where σ is the surface charge density.

Application of Gauss’s Law – Video Lesson

Electric Field Due to Infinite Wire – Gauss Law Application

Consider an infinitely long line of charge with the charge per unit length being λ. We can take advantage of the cylindrical symmetry of this situation. By symmetry, The electric fields all point radially away from the line of charge, and there is no component parallel to the line of charge.

We can use a cylinder (with an arbitrary radius (r) and length (l)) centred on the line of charge as our Gaussian surface .

Electric Field due to Infinite long line of charge

Applications of Gauss Law – Electric Field Due to Infinite Wire

As you can see in the above diagram, the electric field is perpendicular to the curved surface of the cylinder. Thus, the angle between the electric field and area vector is zero and cos θ = 1.

The top and bottom surfaces of the cylinder lie parallel to the electric field. Thus, the angle between the area vector and the electric field is 90 degrees, and cos θ = 0.

Thus, the electric flux is only due to the curved surface.

According to Gauss law,

Φ = → E.d → A

Φ = Φ curved + Φ top + Φ bottom

Φ = → E . d → A = ∫E . dA cos 0 + ∫E . dA cos 90° + ∫E . dA cos 90°

Φ = ∫E . dA × 1

Due to radial symmetry, the curved surface is equidistant from the line of charge, and the electric field on the surface has a constant magnitude throughout.

Φ = ∫E . dA = E ∫dA = E . 2πrl

The net charge enclosed by the surface is

q net = λ.l

Using Gauss theorem,

Φ = E × 2πrl = q net /ε 0 = λl/ε 0

E × 2πrl = λl/ε 0

E = λ/2πrε 0

⇒ Also Read: Electric Potential Energy

Problems on Gauss Law

Problem 1: A uniform electric field of magnitude E = 100 N/C exists in the space in the X-direction. Using the Gauss theorem, calculate the flux of this field through a plane, square area of edge 10 cm placed in the Y-Z plane. Take the normal along the positive X-axis to be positive.

The flux Φ = ∫ E.cosθ ds

As the normal to the area points along the electric field, θ = 0

Also, E is uniform so, Φ = E.ΔS = (100 N/C) (0.10m) 2 = 1 N-m 2

Problem 2: A large plane charge sheet having surface charge density σ = 2.0 × 10 -6 C-m -2 lies in the X-Y plane. Find the flux of the electric field through a circular area of radius 1 cm lying completely in the region where x, y and z are all positive and with its normal, making an angle of 60 0 with the Z-axis.

The electric field near the plane charge sheet is E = σ/2ε 0 in the direction away from the sheet. At the given area, the field is along the Z-axis.

The area = πr 2 = 3.14 × 1 cm 2 = 3.14 × 10 -4 m 2 .

The angle between the normal to the area and the field is 60 0 .

= E.ΔS cos θ

= σ/2ε 0 × pr 2 cos 60º

Problem 3: A charge of 4×10 -8 C is distributed uniformly on the surface of a sphere of radius 1 cm. It is covered by a concentric, hollow conducting sphere of radius 5 cm.

Find the electric field at a point 2 cm away from the centre.
A charge of 6 × 10 -8 C is placed on the hollow sphere. Find the surface charge density on the outer surface of the hollow sphere.

(a) Let us consider figure (i).

Suppose we have to find the field at point P. Draw a concentric spherical surface through P. All the points on this surface are equivalent; by symmetry, the field at all these points will be equal in magnitude and radial in direction.

= 4π x 2 E

Where x = 2 cm = 2 × 10 -2 m

From the Gauss law, this flux is equal to the charge q contained inside the surface divided by ε 0 . Thus,

⇒ 4π x 2 E = q/ε 0 or, E = q/4πε 0 x 2

= ( 9 × 10 9 ) × [(4 × 10 -8 )/(4 × 10 -4 )] = 9 × 10 5 N C -1 .

(b) Let us consider figure (ii).

Take the Gaussian surface through the material of the hollow sphere. As the electric field in a conducting material is zero, the flux $\begin{array}{l}\oint{\overset{\to }{\mathop{E}}\,.d\overset{\to }{\mathop{S}}\,}\end{array} $ through this Gaussian surface is zero.

Using Gauss law, the total charge enclosed must be zero. Hence, the charge on the inner surface of the hollow sphere is 4 × 10 -8 C.

But the total charge given to this hollow sphere is 6 × 10 -8 C. Hence, the charge on the outer surface will be 10 × 10 -8 C.

Problem 4: The figure shows three concentric thin spherical shells, A, B and C, of radii a, b and c, respectively. Shells A and C are given charges q and -q, respectively, and shell B is earthed. Find the charges appearing on the surfaces of B and C.

As shown in the previous worked-out example, the inner surface of B must have a charge -q from the Gauss law. Suppose the outer surface of B has a charge q’.

The inner surface of C must have a charge -q’ from Gauss law. As the net charge on C must be -q, its outer surface should have a charge q’ – q. The charge distribution is shown in the figure.

The potential at B,

Due to the charge q on A = q/4πε 0 b
Due to the charge -q on the inner surface of B = -q/4πε 0 b
Due to the charge q’ on the outer surface of B = q’/4πε 0 b
Due to the charge -q’, on the inner surface of C = -q’/4πε 0 c
Due to the charge q’ – q on the outer surface of C = (q’ – q)/4πε 0 c

The net potential is, VB = q’/4πε 0 b – q/4πε 0 c

This should be zero as shell B is earthed . Thus, q’ = q × b/c

The charges on various surfaces are shown in the figure below.

Problem 5: A particle of mass 5 × 10 -6 g is kept over a large horizontal sheet of charge of density 4.0 × 10 -6 C/m 2 (figure). What charge should be given to this particle so that if released, it does not fall down? How many electrons are to be removed to give this charge? How much mass is decreased due to the removal of these electrons?

The electric field in front of the sheet is

E = σ/2ε 0 = (4.0 × 10 -6 )/(2 × 8.85 × 10 -12 ) = 2.26 × 10 5 N/C

If a charge q is given to the particle, the electric force qE acts in the upward direction. It will balance the weight of the particle , if

q × 2.26 × 10 5 N/C = 5 × 10 -9 kg × 9.8 m/s 2

or, q = [4.9 × 10 -8 ]/[2.26 × 10 5 ]C = 2.21 × 10 -13 C

The charge on one electron is 1.6 × 10 -19 C. The number of electrons to be removed

= [2.21 × 10 -13 ]/[1.6 × 10 -19 ] = 1.4 × 10 6

Mass decreased due to the removal of these electrons = 1.4 × 10 6 × 9.1 × 10 -31 kg = 1.3 × 10 -24 kg.

Problem 6: Two conducting plates, A and B, are placed parallel to each other. A is given a charge Q1, and B a charge Q2. Find the distribution of charges on the four surfaces.

Consider a Gaussian surface, as shown in figure (a). Two faces of this closed surface lie completely inside the conductor where the electric field is zero.

The flux through these faces is, therefore, zero. The other parts of the closed surface, which are outside the conductor, are parallel to the electric field, and hence, the flux on these parts is also zero.

The total flux of the electric field through the closed surface is, therefore, zero. From the Gauss law, the total charge inside the closed surface should be zero. The charge on the inner surface of A should be equal and opposite to that on the inner surface of B.

The distribution should be like the one shown in figure (b). To find the value of q, consider the field at point P inside plate A. Suppose the surface area of the plate (one side) is A.

Using the equation E = σ/2ε 0 , the electric field at P

Due to the charge Q1 – q = (Q1 – q)/2Aε 0 (downward)
Due to the charge +q = q/2Aε 0 (upward)
Due to the charge -q = q/2Aε 0 (downward)
Due to the charge Q2 + q = (Q2 + q)/2Aε 0 (upward)

The net electric field at P due to all the four charged surfaces is (in the downward direction).

(Q1 – q)/2Aε 0 – q/2Aε 0 + q/2Aε 0 – (Q2 + q)/2Aε 0

As point P is inside the conductor, this field should be zero.

Hence, Q1 – q – Q2 – q = 0

or q = (Q1 – Q2)/2 . . . . . (i)

Thus, Q1 – q = (Q1 + Q2)/2 . . . . . . (ii)

and Q2 + q = [Q1 + Q]2/2

Using these equations, the distribution shown in figures (a, b) can be redrawn as in the figure.

This result is a special case of the following result. When charged conducting plates are placed parallel to each other, the two outermost surfaces get equal charges, and the facing surfaces get equal and opposite charges.

Problem 7: A solid conducting sphere having a charge Q is surrounded by an uncharged concentric conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be V. What will be the new potential difference between the same two surfaces, if the shell is given a charge -3Q?

In the case of a charged conducting sphere,

V in = V c = V s = 1/4πε 0

and V out = 1/4πε 0

So, if a and b are the radii of a sphere and spherical shell, respectively, the potential at their surfaces will be

Vsphere = 1/4πε 0 [Q/a] and Vshell = 1/4πε 0 [Q/b] and so according to the given problem,

V = V’sphere – V’shell = Q/4πε 0 [1/a – 1/b] = V . . . . . . . (1)

Now, when the shell is given a charge (-3Q), the potential at its surface and also inside will change by

i.e., if any charge is given to the external shell, the potential difference between the sphere and shell will not change.

This is because by the presence of charge on the outer shell, potential everywhere inside and on the surface of the shell will change by the same amount, and hence, the potential difference between sphere and shell will remain unchanged.

Keeping in mind that here, both electric and gravitational potential energy is changing, and for an external point, a charged sphere behaves as if the whole of its charge were concentrated at its centre.

Applying the law of conservation of energy between the initial and final position, we have

1/4πε 0 × (q.q/9) + mg × 9 = (1/4πε 0 ) x(q 2 /1) + mg × 1

or, q 2 = (80 × 10 -3 × 9.8)/10 9 = 28μC.

Gauss’ Law and Conductors – Short Notes for Quick Revision

Gauss Law and Its Applications – Video Lesson

Solved Questions on Gauss Law

How is the gauss law related to coulomb’s law .

One of the fundamental relationships between the two laws is that the Gauss law can be used to derive Coulomb’s law and vice versa. We can further say that Coulomb’s law is equivalent to the Gauss law, meaning they are almost the same. While this relation is discussed extensively in electrodynamics , we will look at a derivation with the help of an example.

Let’s take a point charge q. Now, if we apply Coulomb’s law, the electric field generated is given by

Where k=1 /4πϵ 0 . If we take the sphere of the radius (r) that is centred on charge q. Now, for the surface S of this sphere, we will have

At the end of the equation, we can see that it refers to the Gauss law. All in all, we can determine the relation between the Gauss law and Coulomb’s law by deducing the spherical symmetry of the electric field and by performing the integration .

How do we choose an appropriate Gaussian surface for different cases?

In order to choose an appropriate Gaussian Surface, we have to take into account the state that the ratio of charge and the dielectric constant is given by a (two-dimensional) surface integral over the electric field symmetry of the charge distribution. There are three different cases that we will need to know about.

Spherical, when the charge distribution is spherically symmetric.
Cylindrical, when the charge distribution is cylindrically symmetric.
Pillbox, when the charge distribution has translational symmetry along a plane.

We can choose the size of the surface depending on where we want to calculate the field. The Gauss theorem is helpful for finding a field when there is a certain symmetry , as it tells us how the field is directed.

How is electric flux related to the Gauss law?

When we talk about the relation between electric flux and Gauss law, the law states that the net electric flux in a closed surface will be zero, if the volume that is defined by the surface contains a net charge.

To establish the relation, we will first take a look at the Gauss law.

If we take the Gauss law, it is represented as

Φ E = Q/ ε o

Φ E = Electric flux through a closed surface S enclosing any volume V
Q = Total charge enclosed within V
ε o = Electric constant

Meanwhile, the electric flux Φ E can now be defined as a surface integral of the electric field. It is given as

Φ E = ∫∫ E . dA

E = Electric field
dA = Vector representing an infinitesimal element of the area of the surface.

Notably, flux is considered an integral of the electric field. This relation or form of the Gauss law is known as the integral form.

What is the differential form of the Gauss theorem?

The differential form of Gauss law relates the electric field to the charge distribution at a particular point in space. To elaborate, as per the law, the divergence of the electric field (E) will be equal to the volume charge density (p) at a particular point. It is represented as

ε o = Permittivity of free space

How to find the electric field using the Gauss law?

Normally, the Gauss law is used to determine the electric field of charge distributions with symmetry. There are several steps involved in solving the problem of the electric field with this law. They are as follows:

First, we have to identify the spatial symmetry of the charge distribution.
The next step involves choosing a correct Gaussian surface with the same symmetry as the charge distribution. Its consequences should also be identified.
Evaluate the integral Φ s E over the Gaussian surface and then calculate the flux through the surface.
Find the amount of charge enclosed by the Gaussian surface.
Evaluate the electric field of the charge distribution.

However, students have to keep in mind the three types of symmetry in order to determine the electric field. The types of symmetry are

Spherical symmetry
Cylindrical symmetry
Planar symmetry

Frequently Asked Questions on Gauss Law

Can the gauss law be applied to all surfaces.

For any closed surface and for any distribution of charges, the Gauss law is valid.

Can the Gauss law be applied to the non-uniform electric field?

The Gauss law can be applied to uniform and non-uniform electric fields.

State the Gauss law.

According to the Gauss law, the net flux of an electric field in a closed surface is directly proportional to the charge enclosed.

What is the factor on which the electric field lines depend?

The Gauss law is interpreted in terms of the electric flux through the surface. The electric flux through the surface is the number of lines of force passing normally through the surface. The electric flux depends on the charge enclosed by the surface.

When is the flux through the surface taken as positive or negative?

The flux through the surface is taken as positive if the flux lines are directed outwards and negative if the flux is directed inwards.

What is called a Gaussian surface?

A Gaussian surface is a surface through which the electric flux is calculated.

Can Coulomb’s law be derived using the Gauss law?

Yes, Coulomb’s law can be derived using the Gauss law and vice-versa.

Define surface charge density.

When the charge is uniformly distributed over the surface of the conductor, it is called surface charge density.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all JEE related queries and study materials

Your result is as below

Request OTP on Voice Call

Register with Aakash BYJU'S & Download Free PDFs

Browse Course Material

Course info, instructors.

Bruce Knuteson
Prof. Eric Hudson
Dr. George Stephans
Prof. John Belcher
Prof. John Joannopoulos
Prof. Michael Feld
Dr. Peter Dourmashkin

Departments

As taught in.

Electromagnetism

Learning Resource Types

Electricity and magnetism, chapte4gauss_law.pdf.

This resource includes the following topics: electric flux, Gauss?s law, conductors, force on a conductor, summary, appendix: tensions and pressures, problem-solving strategies, solved problems, conceptual questions, and additional problems.

You are leaving MIT OpenCourseWare

Games & Quizzes
History & Society
Science & Tech
Biographies
Animals & Nature
Geography & Travel
Arts & Culture
On This Day
One Good Fact
New Articles
Lifestyles & Social Issues
Philosophy & Religion
Politics, Law & Government
World History
Health & Medicine
Browse Biographies
Birds, Reptiles & Other Vertebrates
Bugs, Mollusks & Other Invertebrates
Environment
Fossils & Geologic Time
Entertainment & Pop Culture
Sports & Recreation
Visual Arts
Demystified
Image Galleries
Infographics
Top Questions
Britannica Kids
Saving Earth
Space Next 50
Student Center
Why does physics work in SI units?
Is mathematics a physical science?

Highway Night Traffic Portland, drive, driving, car, automobile.

Gauss’s law

Our editors will review what you’ve submitted and determine whether to revise the article.

California Information of Technology - The Feynman Lectures on Physics - Application of Gauss’ Law
University of Saskatchewan - Introduction to Electricity, Magnetism, and Circuits - Explaining Gauss’s Law
University of California - Gauss's Law
United States Nuclear Regulatory Commission - Physical and Chemical Properties of Tritium
Khan Academy - Gauss's law
University of Central Florida Pressbooks - University Physics Volume 2 - Applying Gauss’s Law
Physics LibreTexts - Gauss’s law

Gauss’s law , either of two statements describing electric and magnetic fluxes. Gauss’s law for electricity states that the electric flux Φ across any closed surface is proportional to the net electric charge q enclosed by the surface; that is, Φ = q /ε 0 , where ε 0 is the electric permittivity of free space and has a value of 8.854 × 10 –12 square coulombs per newton per square metre. The law implies that isolated electric charges exist and that like charges repel one another while unlike charges attract. Gauss’s law for magnetism states that the magnetic flux B across any closed surface is zero; that is, div B = 0, where div is the divergence operator. This law is consistent with the observation that isolated magnetic poles ( monopoles ) do not exist.

Mathematical formulations for these two laws—together with Ampère’s law (concerning the magnetic effect of a changing electric field or current ) and Faraday’s law of induction (concerning the electric effect of a changing magnetic field )—are collected in a set that is known as Maxwell’s equations , which provide the foundation of unified electromagnetic theory.

Applications of Gauss’s Law

Now that you have a brief idea of what Gauss law is, let us look at the application of Gauss Law . Does that already look difficult to you? Well, no! We will make it easier for you! It is important to note that we can use Gauss’s Law to solve complex electrostatic problems involving unique symmetries like cylindrical, spherical or planar symmetry. So, contrary to what you thought, the application of Gauss Law can actually make your task easier!

Browse more Topics under Electric Charges And Fields

Conductors and Insulators
Electric Charge
Basic Properties of Electric Charge
Coulomb’s Law
Electric Field
Electric Field Lines
Gauss’s Law
Electric Flux
Electric Dipole
Dipole in a Uniform External Field

Electric Field due to Infinite Wire

Let us consider an infinitely long wire with linear charge density λ and length L. To calculate electric field, we assume a cylindrical Gaussian surface. As the electric field E is radial in direction, the flux through the end of the cylindrical surface will be zero.

This is because the electric field and area vector are perpendicular to each other. As the electric field is perpendicular to every point of the curved surface, we can say that its magnitude will be constant.

The surface area of the curved cylindrical surface is 2πrl. The electric flux through the curve is

According to Gauss’s Law

You need to remember that the direction of the electric field is radially outward if linear charge density is positive. On the other hand, it will be radially inward if the linear charge density is negative.

Electric Field due to Infinite Plate Sheet

Let us consider an infinite plane sheet, with surface charge density σ and cross-sectional area A. The position of the infinite plane sheet is as below:

The direction of the electric field due to an infinite charge sheet is perpendicular to the plane of the sheet. Let us consider a cylindrical Gaussian surface, whose axis is normal to the plane of the sheet. We can evaluate the electric field E from Gauss’s Law as according to the law:

Froma continuous charge distribution charge q will be the charge density (σ) times the area (A). Talking about net electric flux, we will consider electric flux only from the two ends of the assumed Gaussian surface. We can attribute it to the fact that the curved surface area and an electric field are normal to each other, thereby producing zero electric flux. So the net electric flux is

Φ = EA – (– EA)

Then, we can write

The term A cancels out which means electric field due to an infinite plane sheet is independent of cross-sectional area A and equals to:

Electric Field due to Thin Spherical Shell

Let us consider a thin spherical shell of surface charge density σ and radius “R”. By observation, we can see that the shell has spherical symmetry. Therefore, we can evaluate the electric field due to the spherical shell in two different positions:

Electric field outside the spherical shell
Electric field inside the spherical shell

Let us look at these two cases in greater detail.

Download Conductors and Insulators Cheat Sheet PDF

Electric Field Outside the Spherical Shell

To find electric field outside the spherical shell, we take a point P outside the shell at a distance r from the centre of the spherical shell. By symmetry, we take Gaussian spherical surface with radius r and centre O. The Gaussian surface will pass through P, and experience a constant electric field E all around as all points are equally distanced “r’’ from the centre of the sphere . Then, according to Gauss’s Law:

The enclosed charge inside the Gaussian surface q will be σ × 4 πR 2 . The total electric flux through the Gaussian surface will be

Φ = E × 4 πr 2

Then by Gauss’s Law, we can write

Putting the value of surface charge density σ as q/4 πR 2 , we can rewrite the electric field as

In vector form, the electric field is

where r is the radius vector, depicting the direction of electric field . What we must note here is that if the surface charge density σ is negative, the direction of the electric field will be radially inward.

Electric Field Inside the Spherical Shell

To evaluate electric field inside the spherical shell, let’s take a point P inside the spherical shell. By symmetry, we again take a spherical Gaussian surface passing through P, centered at O and with radius r. Now according to Gauss’s Law

The net electric flux will be E × 4 π r 2 .

Solved Example for You

Question: Why is there no electric field inside a spherical shell?

Solution: The enclosed charge q will be zero, as we know that surface charge density is dispersed outside the surface, therefore there is no charge inside the spherical shell. Therefore, E = 0

This concludes our discussion on the topic of application of Gauss Law.

Customize your course in 30 seconds

Which class are you in.

Electric Charges and Fields

Charge Transfer
Electroscope
Resistor Colour Codes
Dipole in a Uniform External Field
Gauss’s Law

Download the App

In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation.

Snapsolve any problem by taking a picture. Try it in the Numerade app?

Understanding Gauss's Law: A Comprehensive Guide Class Lectures

Bootcamp Curriculum

Understanding gauss's law: a comprehensive guide lecture videos, solved step-by-step.

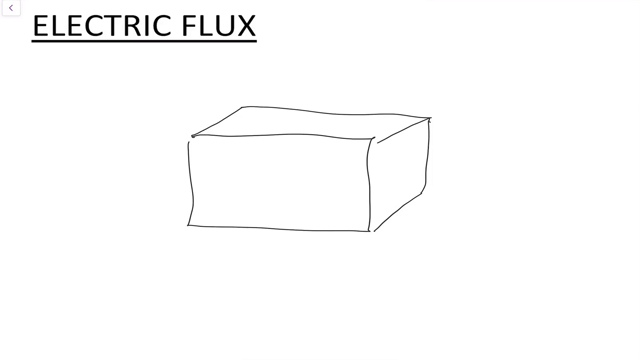
Electric Flux

Gauss's Law II

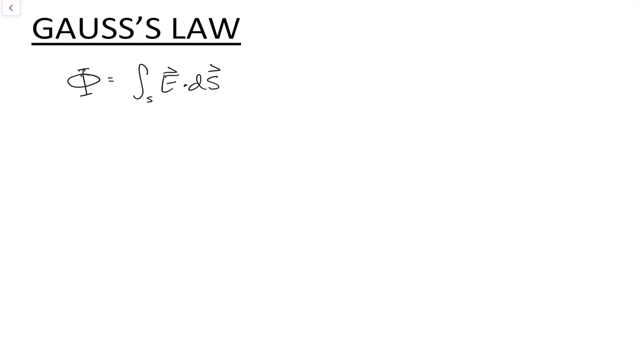
Gauss's Law Example

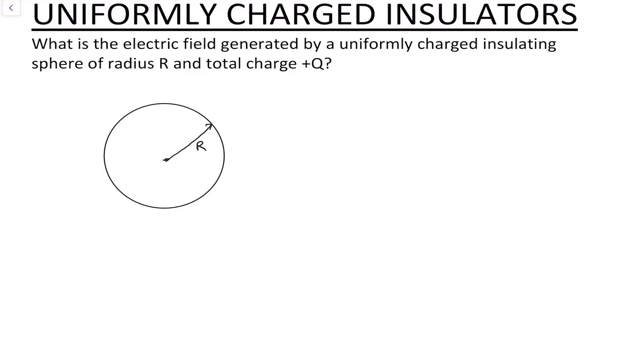
Uniformly Charged Insulators

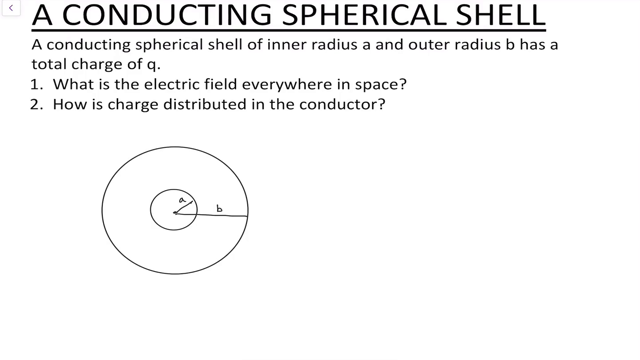
Conducting Spherical Shell

Recommended courses.

What our students say

Join our STEM bootcamps

Create a free account to access our STEM bootcamps

A free answer just for you

Watch the video solution with this free unlock.

Log in to watch this video ...and 100,000,000 more!

Physics Project On ‘Gauss Theorem’ For Class 12

Table of Contents

Acknowledgment

I’d like to take a moment to extend my heartfelt gratitude to some incredible folks and resources that played a pivotal role in bringing this Gauss’s Theorem project to a triumphant close.

First and foremost, a massive shout-out to my physics mentor, [Teacher’s Name]. Their guidance, endless patience, and sheer brilliance were like a guiding light through the twists and turns of this project. They not only helped me make sense of this intricate subject but also welcomed my countless questions with open arms.

I can’t forget my fantastic classmates. Our enlightening discussions and brainstorming sessions were like refining fire for the ideas and content presented in this project. Teamwork truly makes the dream work.

My family deserves a special mention. Their unwavering support and understanding throughout this project have been my rock. Their faith in my abilities has been a constant source of inspiration and motivation.

Huge props to the authors of those textbooks and research papers I delved into for reference and insight. Their groundbreaking work laid the groundwork for my research and provided those essential ‘Aha!’ moments.

Last but not least, kudos to the online academic community. You folks offered a treasure trove of resources and engaging discussions about all things Gauss’s Theorem. You’re the unsung heroes in this academic journey.

To each and every one of you, I extend my heartfelt thanks. Your support and encouragement have been the driving force behind the triumphant completion of this project.

With gratitude,

Introduction to Gauss’s Theorem

Let’s dive into the fascinating realm of Gauss’s Theorem, a mathematical gem that goes by another moniker, Gauss’s Divergence Theorem. This concept isn’t just any run-of-the-mill idea; it’s a cornerstone of vector calculus and electromagnetism, holding the key to unlocking the secrets of electric and magnetic fields in our three-dimensional universe. And, of course, we tip our hats to none other than the brilliant Carl Friedrich Gauss for giving it his name.

So, what’s the scoop on Gauss’s Theorem? Well, imagine it as a bridge—a powerful, mathematical bridge—that connects the behavior of a vector field (like those electric and magnetic fields we’re always talking about) inside a closed space to what’s happening on the surface that wraps around that space. It’s like peeking inside a magic box and understanding how the magic works on the outside.

Now, why is this theorem such a rock star in the world of physics, especially when we’re talking about electromagnetism? The answer is versatility. Gauss’s Theorem steps up to the plate in a wide array of scenarios, helping us untangle the mysteries of complex electromagnetism problems.

At its core, this theorem waltzes through the notion of flux. Flux, in this context, is all about measuring how a vector field flows through a surface. When we apply this concept to electric fields, it lets us in on the secret of how electric charges organize themselves within a closed space and how that arrangement influences the electric field at various points inside. And guess what? It does a similar magic trick with magnetic fields, revealing how magnetic sources pull the strings of those field lines within a closed region.

So there you have it, Gauss’s Theorem in a nutshell—a mathematical tour de force that helps us decode the intricate dance of electric and magnetic fields in the vast canvas of three-dimensional space.

Gauss’s Law

Gauss’s Law, a true heavyweight in the world of electromagnetism, is like the close cousin of Gauss’s Theorem. This powerhouse principle is your go-to tool for unraveling the mysteries of electric fields caused by electric charges. All thanks to the mathematical genius Carl Friedrich Gauss for giving us this gem.

Now, let’s get down to the nitty-gritty with Gauss’s Law. This law is all about giving us the mathematical scoop on how electric charges are distributed and how they create those electric fields that surround them.

The Mathematical Magic of Gauss’s Law: Gauss’s Law, in its mathematical glory, looks like this:

∮E⋅dA = (Q_enclosed) / ε₀

Here’s the lowdown on the lingo:

∮E⋅dA is a fancy way of saying we’re doing a surface integral of the electric field E over a closed surface.
Q_enclosed is the total electric charge hanging out inside that closed surface.
ε₀ (epsilon naught) is the electric constant, also known as vacuum permittivity, clocking in at roughly 8.854 x 10⁻¹² C²/N·m² in SI units.

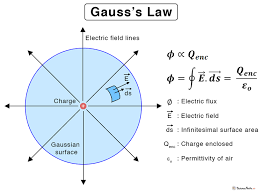
Cracking the Code of Gauss’s Law:

What Gauss’s Law is spilling the beans on is this: The total electric flux (which is basically the integral of the electric field over a closed surface) equals the sum total of electric charge sealed up within that surface, all divided by ε₀. It’s like counting the number of electric field lines that either start from or end on electric charges.

Now, let’s wrap our heads around a few key points:

Flux and Electric Field: Electric flux measures how many electric field lines cozy up to a closed surface. The law tells us how this is connected to the charge inside and gives us a glimpse into the electric field’s strength and direction.
Closed Surfaces: Gauss’s Law loves to work with closed surfaces. These surfaces are chosen carefully to make our math easy-peasy, based on how the charges are spread out.
Symmetry: When dealing with charge distributions that are all neat and symmetric, like spheres, cylinders, or planes, Gauss’s Law is your superhero. It turns complex electric field calculations into a walk in the park.

Where Gauss’s Law Shines:

Electric Field of Point Charges: Gauss’s Law is your buddy when figuring out the electric field due to point charges, whether it’s one charge or a bunch of them.
Electric Field of Symmetric Charge Distributions: It’s like a secret shortcut for calculating electric fields when things are all symmetric, like charged spheres or infinite planes.
Detecting Charge Distributions: When you know the electric field, Gauss’s Law can help you play detective and find out how the charges are distributed inside a closed surface.
Charge Conservation Checks: It’s the lie detector test for electric charge conservation within a closed area.

Closed Surfaces and the Dance of Electric Charges

In the magnificent world of Gauss’s Law and its electrifying applications, grasping the concept of closed surfaces and the art of arranging electric charges is absolutely key. These two pieces of the puzzle are like the dynamic duo in our quest to unlock the secrets of electric fields. So, let’s dive into the details:

Closed Surfaces:

Picture a closed surface as a magical three-dimensional boundary that wraps itself around a specific chunk of space. It’s like a cosmic fence that separates the zone we’re interested in from the great beyond. When we’re wielding Gauss’s Law, we’re pretty picky about which closed surface to choose. It’s all about making our math as smooth as silk, and we often pick surfaces that match the charge distribution’s symmetry. Think spheres, cylinders, and cubes for starters.

Charge Distributions:

Charge distributions are like the choreography of electric charges within a designated area of space. They can take on various forms, like point charges (those solo acts), line charges (the linear performers), surface charges (the ones spread out like a canvas), or volume charges (the stars of the show). Why do they matter? Well, they’re the architects of the electric field in town.

Now, let’s connect the dots between these concepts and Gauss’s Law:

Picking the Right Closed Surface: When we’re throwing Gauss’s Law into action, the first order of business is choosing the perfect closed surface. We’re matchmakers here, pairing the surface with the symmetry of the charge distribution. For instance:

For a single point charge, we often go for a spherical closed surface centered on the charge because it’s beautifully spherical.
When we’re dealing with an infinite plane packed with charges, a cylindrical closed surface with one end kissing the plane is our go-to choice. Why? Symmetry, my friend.

Cracking the Code of Electric Flux: Gauss’s Law connects the total electric flux (that’s the integral of the electric field over the closed surface) to the net charge cozying up inside the surface. It’s like counting the electric field lines that pass through the surface and relating them to the charge inside the cosmic boundary.

Symmetry the Simplifier: Choosing a closed surface that’s symmetrical to the charge distribution is like finding a shortcut in a maze. In these cases, the electric field often behaves like a well-behaved child, being consistent in magnitude and direction across the closed surface. This makes calculating flux a breeze.

A Law for All Seasons: Gauss’s Law isn’t picky. It plays nice with all kinds of charge distributions. Whether it’s a point charge, a charged sphere, an endless charged wire, or any other electric charge scenario, Gauss’s Law can step in and reveal the electric field’s secrets.

Detective Work: In some situations, Gauss’s Law can even be flipped around. If we know the electric field, it can lend a hand in figuring out the charge distribution within a closed surface. It’s like solving a mystery in reverse.

Gauss’s Theorem

Gauss’s Theorem, also affectionately known as Gauss’s Divergence Theorem, is like a magical wand in the world of electromagnetism. It’s the brainchild of none other than the genius Carl Friedrich Gauss, and it’s the key that unlocks the mysteries of electric fields by dancing with electric charges within a closed volume. Let’s dive into the enchanting realm of Gauss’s Theorem for electric fields:

The Mathematical Charm of Gauss’s Theorem for Electric Fields:

Gauss’s Theorem elegantly states:

∮E⋅dA = (1 / ε₀) ∫∫∫ρ dV

Let’s break it down:

∮E⋅dA is like a fancy way of saying we’re doing a surface integral of the electric field E over a closed surface.
ε₀ (epsilon naught) is our mystical constant, also known as vacuum permittivity, which stands at approximately 8.854 x 10⁻¹² C²/N·m² in SI units.
∫∫∫ρ dV is our volume integral of charge density ρ, covering the closed volume embraced by that surface.

Decoding Gauss’s Theorem for Electric Fields

What this theorem is whispering to us is this: The total electric flux (that’s the integral of the electric field over the closed surface) is like a cosmic bill, and it equals the total electric charge tucked away inside that cosmic surface, all divided by ε₀. It’s like tallying how many electric field lines start or end on electric charges within a sealed region.

Now, let’s shine a light on some key insights:

Flux and Electric Field: The left side of our equation (∮E⋅dA) is all about electric flux—it measures how electric field lines cross a closed surface, like counting sunbeams through a window.
Charge Density: On the right side (∫∫∫ρ dV), we’re digging into the charge density ρ. It tells us how electric charges are scattered within the closed volume, like a treasure hunt for electric charge.
The Magic ε₀: ε₀, our trusty constant, makes sure the units of charge and electric field play nicely together. It’s the glue that holds the equation’s dimensions in place.

Where Gauss’s Theorem Shines for Electric Fields

Electric Fields of Symmetry: Gauss’s Theorem really struts its stuff when we’re dealing with symmetrical charge setups, think charged spheres or fancy cylinders. In these cases, it’s like the math fairy granting our wishes for simplified electric field calculations.
Gauss’s Law Validation: Gauss’s Theorem is the rock-solid foundation upon which Gauss’s Law stands. When we use it on a surface that’s shielding no charge (∫∫∫ρ dV = 0), Gauss’s Theorem nods in agreement with Gauss’s Law, which tells us the electric field divergence is zilch where no charges roam.
Peeking Inside Enclosures: The theorem gives us a backstage pass to understand how electric field lines swirl and twirl around various charge collections enclosed by surfaces, and how those tucked-away charges call the shots.

Examples and Problem Solving

Let’s Solve Some Electric Field Mysteries: Examples and Problem-Solving

To truly wrap our heads around Gauss’s Theorem for electric fields, we’re diving into the exciting world of real-world examples and solving problems that put this theorem to work. Get ready for some illuminating scenarios:

Example 1: The Electric Field of a Point Charge

Scenario: Imagine we’ve got a point charge ‘Q’ hanging out at a distance ‘r’ from us, and we want to figure out the electric field it’s creating using Gauss’s Theorem.

We start by picking a closed surface that wraps around our point charge. In this case, a spherical surface centered on the charge is perfect because it’s symmetrical.
We roll out Gauss’s Theorem and calculate the electric flux (∮E⋅dA) across our spherical surface.
Since the electric field behaves the same in all directions (radially symmetric), the math simplifies. We look at E⋅dA as E * dA * cos(θ), where θ is the angle between the electric field and the surface’s normal.
Now, we find the electric field’s magnitude on our spherical surface: E = (Q_enclosed) / (4πε₀r²).
Let’s integrate and calculate the flux over the spherical surface.
Finally, we set the flux equal to the right side of Gauss’s Theorem and solve for our electric field ‘E.’

Example 2: The Electric Field of an Infinite Charged Plane

Scenario: We’re standing a distance ‘d’ away from an infinite charged plane with a uniform charge density ‘σ,’ and we’re curious about the electric field at point ‘P.’ Gauss’s Theorem to the rescue!

To make our lives easier, we choose a Gaussian surface that plays nicely with the problem’s symmetry. In this case, a cylindrical Gaussian surface perpendicular to the plane and centered at ‘P’ fits the bill.
We put Gauss’s Theorem to work again, this time calculating the electric flux (∮E⋅dA) through our cylindrical surface.
We peek inside our Gaussian surface to find the enclosed charge, which is Q_enclosed = σ * A, with ‘A’ as the circular end’s area of the cylinder.
The electric field here points straight through our cylindrical surface, so E⋅dA is just E * dA.
We express the flux in terms of the electric field and the cylinder’s surface area.
Next, we equate the flux to the right side of Gauss’s Theorem and work our magic to find the electric field ‘E’ at point ‘P.’

Problem-Solving Wisdom:

Symmetry is your best friend; choose Gaussian surfaces that make the math simpler.
Never forget to spot the charge lurking inside your chosen Gaussian surface.
Keep units and constants like ε₀ in check for a hassle-free solution.
A keen eye for detail in your mathematical steps ensures accuracy.
Visualize the problem using diagrams; it makes everything clearer.

Applications in Electromagnetism

The Versatility of Gauss’s Theorem in Electromagnetism

Gauss’s Theorem isn’t just a mathematical gem; it’s the secret weapon in the world of electromagnetism. This versatile tool simplifies the complex and untangles the mysteries of electric and magnetic fields. Let’s uncover its applications in the realm of electromagnetism:

Electric Flux and Gauss’s Law:

Gauss’s Law for Electricity: Gauss’s Theorem is the star player in Gauss’s Law for electricity. It’s the key to finding electric fields from various charge distributions, from simple point charges to the intricate geometry of charged spheres and infinite planes. This law is the backbone of understanding how electric fields influence charges and the workings of electric circuits.

Electric Field of Symmetric Charge Distributions:

Charged Spheres: Gauss’s Theorem makes light work of calculating the electric field both inside and outside charged conducting spheres. This is essential for understanding the behavior of conductors and their interactions with electric fields.

Electric Field of Infinite Planes:

Uniformly Charged Infinite Planes: Ever wondered about the electric field near and far from an infinite uniformly charged plane? Gauss’s Theorem is the compass guiding us through this exploration. It’s vital for understanding how electric fields behave near vast conducting surfaces, like Earth’s surface during lightning strikes.

Electric Field in Insulating Materials:

Dielectrics: Gauss’s Theorem is our guide when electric fields penetrate insulating materials (dielectrics). It helps us understand how electric fields are affected by induced charges on the dielectric’s surfaces. This knowledge is crucial in the study of capacitors and the behavior of dielectric materials.

Electric Field and Symmetry:

Symmetric Charge Distributions: Gauss’s Theorem is at its best when tackling symmetric charge arrangements. Whether it’s spheres, cylinders, or planes, it simplifies electric field calculations and is a go-to tool for solving real-world problems.

Magnetic Field of Permanent Magnets:

Gauss’s Law for Magnetism: Although magnetic monopoles don’t exist, Gauss’s Theorem still has a role to play in certain magnetic field scenarios. Gauss’s Law for Magnetism tells us that magnetic field lines always form closed loops. It’s this theorem that helps us understand why there are no isolated magnetic charges and why the total magnetic flux through a closed surface is always zero.

Magnetic Field of Symmetric Current Distributions:

Ampère’s Law: Gauss’s Theorem teams up with Ampère’s Law to uncover the magnetic field around symmetric current distributions. Think long straight wires or solenoids. This duo is essential for designing electromagnets and deciphering magnetic field behaviors in circuits.

Applications in Electromagnetic Theory:

Maxwell’s Equations: Gauss’s Theorem isn’t just a side character; it’s a foundational element of Maxwell’s equations. These four equations are the heartbeat of electromagnetic theory. Gauss’s Theorem provides the mathematical groundwork for these equations, allowing us to harmoniously describe all things electromagnetic.

Limitations and Assumptions

As we harness the power of Gauss’s Theorem in the electrifying world of electromagnetism, it’s crucial to be aware of its limitations and the assumptions it carries. Let’s shine a light on these caveats to ensure the theorem’s accuracy and relevance in practical applications. Here are the key points to bear in mind:

Closed Surfaces: Gauss’s Theorem is your trusty sidekick for closed surfaces. It doesn’t play well with open surfaces or those that stretch out into the infinite unknown. So, always choose a closed surface for Gauss’s Theorem to work its magic.
Symmetry: Gauss’s Theorem thrives on symmetry. It’s at its peak when dealing with symmetric charge or current distributions. When symmetry takes a back seat, applying the theorem can be a bit of a puzzle, requiring a breakdown into more symmetric components.
Charge Distribution: Gauss’s Theorem assumes a continuous charge distribution. It loves the macroscopic, continuous world but might stumble when dealing with discrete charges or ultra-fine-grained distributions like individual electrons.
Charge Conservation: Implicitly, the theorem assumes the conservation of electric charge. It doesn’t handle scenarios involving changing charge distributions or non-conservative systems where charges might pop in or vanish.
Linearity of Electric Fields: Gauss’s Theorem believes in the power of superposition. It assumes that the total electric field at a point is the sum of the electric fields from individual charges or charge distributions. But in exotic realms near black holes or within quantum electrodynamics, this assumption might not hold.
Electrostatic Conditions: Gauss’s Theorem is in its element in electrostatic scenarios, where charges are peacefully at rest. In dynamic situations with changing electric and magnetic fields, this theorem might not be the hero you need. Maxwell’s equations, the extended version, would be your go-to.
Absence of Magnetic Monopoles: Gauss’s Theorem takes a firm stance against magnetic monopoles. It believes in the cosmic balance, where magnetic field lines always form loops, and there are no lone magnetic charges. This is a fundamental pillar of electromagnetic theory.
Continuity and Differentiability: Gauss’s Theorem speaks the language of continuity and differentiability. It assumes that electric fields and charge densities within the chosen volume are well-behaved. If there are abrupt changes or singularities, the theorem might raise an eyebrow.

Gauss’s Theorem and Maxwell’s Equations

In the grand symphony of classical electromagnetism, Gauss’s Theorem takes center stage, serving as the pivotal link that connects us to Maxwell’s equations. These equations are the bedrock of our understanding of how electric and magnetic fields dance in response to charges and currents. Let’s explore the profound connection between Gauss’s Theorem and two of Maxwell’s equations: Gauss’s Law for Electricity and Gauss’s Law for Magnetism.

Gauss’s Law for Electricity:

Gauss’s Theorem Connection: Gauss’s Theorem lays the very groundwork for Gauss’s Law for Electricity, also known as Gauss’s first equation. This law elegantly tells us that the electric flux through a closed surface is intimately tied to the total electric charge enclosed within that surface. Mathematically, it whispers: ∮E⋅dA = (1 / ε₀) ∫∫∫ρ dV
Maxwell’s Equation: Within the sacred text of Maxwell’s equations, Gauss’s Law for Electricity is one of the cornerstones. It quantifies how electric fields emerge from electric charges and how the electric field’s divergence is influenced by the charge density (ρ).

Gauss’s Law for Magnetism:

Gauss’s Theorem Connection: While not a direct offspring of Gauss’s Theorem, Gauss’s Law for Magnetism pays homage to it. It states that magnetic field lines are eternal loops, with no solo magnetic charges wandering the universe. Thus, the total magnetic flux through any closed surface forever remains at zero.
Maxwell’s Equation: This law finds its home in Maxwell’s equations as well. Formally, it is presented as: ∮B⋅dA = 0
Ampère’s Circuital Law: To complete the tale of magnetic forces, we turn to Ampère’s Circuital Law, another luminary in Maxwell’s equations. It narrates how magnetic fields circulate and interact with electric currents.

Connection to the Entire Maxwell’s Equations:

Holistic Understanding: While Gauss’s Theorem graciously lends its wisdom to Gauss’s Laws, the full ensemble of Maxwell’s equations comprises four harmonious equations. Alongside Gauss’s Laws, we have Faraday’s Law of Electromagnetic Induction and the Ampère-Maxwell Law.
Comprehensive Description: These four equations weave a tapestry that captures the essence of electromagnetic phenomena. They reveal how electric and magnetic fields are born, how they traverse space, and how they react to the ebb and flow of charges and currents.

In our journey through the intricate realms of electromagnetism, we’ve ventured deep into the heart of Gauss’s Theorem and its profound applications. This exploration has illuminated the core principles, mathematical intricacies, and practical significance of this fundamental theorem, paying homage to its namesake, Carl Friedrich Gauss. As we conclude, let’s recap the pivotal insights gleaned from our odyssey:

Foundations of Gauss’s Theorem:

Gauss’s Theorem, or Gauss’s Divergence Theorem, is the compass guiding our understanding of electric and magnetic fields. It unveils the intrinsic relationship between the flux of a vector field (such as electric or magnetic fields) across a closed surface and the field’s divergence within an enclosed volume.

Mathematical Formulation:

In the realm of electric fields, Gauss’s Theorem is elegantly inscribed as ∮E⋅dA = (1 / ε₀) ∫∫∫ρ dV, where E denotes the electric field, ε₀ stands as the electric constant, ρ signifies the charge density, and the integrals sweep across a closed surface and its enshrined volume.

Electric Field Chronicles:

Gauss’s Theorem’s prowess shines when discerning electric fields arising from diverse charge distributions. It unveils the secrets behind point charges, charged spheres, and infinite planes, offering clarity in the realm of electrostatics.
Symmetry becomes our ally, simplifying calculations and rendering Gauss’s Theorem indispensable in scenarios adorned with geometric harmony.

Magnetic Fields and the Gauss’s Embrace:

While magnetic fields also engage with Gauss’s Theorem, they do so with the caveat of a magnetic monopole-free universe. It proclaims that the sumptuous magnetic flux through any closed surface forever dances to the tune of zero.

Harmonious Overture to Maxwell’s Equations:

Gauss’s Theorem extends its benevolence to the illustrious Maxwell’s equations, particularly enfolding Gauss’s Laws for Electricity and Magnetism within its mathematical embrace.
These equations, born of the union between Gauss’s wisdom and the principles of electromagnetism, unveil the intimate connection between electric and magnetic fields, charges, and currents.

Limits and Assumptions:

Every theorem, no matter how profound, bears limitations. Gauss’s Theorem finds its boundaries, often in the form of closed surfaces and the refuge of symmetry.

Electromagnetic Terrain Exploration:

In the grand tapestry of electromagnetism, Gauss’s Theorem finds its purpose in an array of applications. It unravels the mysteries of electric and magnetic fields around charges, conductors, dielectrics, and the enchanting realm of current-carrying wires.

Certificate of Completion

This is to certify that I, [Student’s Name], a [Class/Grade Level] student, have successfully completed the project on ” Gauss Theorem For Class 12.” The project explores the fundamental principles and key aspects of the chosen topic, providing a comprehensive understanding of its significance and implications.

In this project, I delved into in-depth research and analysis, investigating various facets and relevant theories related to the chosen topic. I demonstrated dedication, diligence, and a high level of sincerity throughout the project’s completion.

Key Achievements:

Thoroughly researched and analyzed Physics Project On ‘Gauss Theorem’ For Class 12. Examined the historical background and evolution of the subject matter. Explored the contributions of notable figures in the field. Investigated the key theories and principles associated with the topic. Discussed practical applications and real-world implications. Considered critical viewpoints and alternative theories, fostering a well-rounded understanding. This project has significantly enhanced my knowledge and critical thinking skills in the chosen field of study. It reflects my commitment to academic excellence and the pursuit of knowledge.

In order to download the PDF, You must follow on Youtube. Once done, Click on Submit

Subscribed? Click on Confirm

Download Physics Project On ‘Gauss Theorem’ For Class 12 PDF

Automated Roti and Puri Maker Press project

The Oil Skimmer RC Boat

Secure Digi Locker Application Project

Software Piracy Protection Project

Please Enable JavaScript in your Browser to Visit this Site.

Intro Physics Homework Help
Advanced Physics Homework Help
Precalculus Homework Help
Calculus Homework Help
Bio/Chem Homework Help
Engineering Homework Help
Homework Help
Introductory Physics Homework Help

Exploring the Limitations of Gauss's Law: A Case Study of a Line Charge in Air

Thread starter TheRedDevil18
Start date Sep 13, 2015
Tags Gauss Gauss law Law Work
Sep 13, 2015

Homework Statement

Homework equations, the attempt at a solution.

Scientists develop new technique for bespoke optical tweezers
New technique offers unprecedented control over light at terahertz frequencies
Researchers realize time reversal through input-output indefiniteness

Gauss method works only if the electric field at any point on the enclosing surface is uniform, which is not in this problem because the wire is of finite length. Use the integration method to integrate the electric field from each line segment along the wire.

blue_leaf77 said: Gauss method works only if the electric field at any point on the enclosing surface is uniform, which is not in this problem because the wire is of finite length. Use the integration method to integrate the electric field from each line segment along the wire.

For the case of finite wire, imagine two points, one located near the left end of the wire, the other located at the center, both point lie on your cylindrical surface The electric field in the first point will tend to be directed to the left or right depending on the charge of the wire. For the point in the middle, it will feel the same amount of electric field from the left and right parts of the wire and hence will be directed perpendicularly to the wire. For the case of infinite wire, no matter where you translate your observation point you will always end up in the same configuration as the wire has no end on both sides.

Another view: your Gaussian cylinder has flux coming out the sides in addition to the length. Gauss's theorem still holds but you can't ignore the side flux.

Related to Exploring the Limitations of Gauss's Law: A Case Study of a Line Charge in Air

1. why doesn't gauss law work for non-uniform electric fields.

Gauss Law only applies to situations where the electric field is constant and uniform. In non-uniform electric fields, the electric field lines are not parallel, making it impossible to use Gauss Law to calculate the electric flux.

2. How come Gauss Law does not apply to magnetic fields?

Gauss Law is a principle that applies specifically to electric fields. The magnetic field has its own set of laws, such as Ampere's Law, which govern its behavior. While there are similarities between electric and magnetic fields, they are fundamentally different and cannot be analyzed using the same principles.

3. Can Gauss Law be used to determine the electric field inside a conductor?

No, Gauss Law cannot be used to determine the electric field inside a conductor. This is because the electric field inside a conductor must be zero, according to the properties of conductors. Gauss Law only applies to situations where the electric field is non-zero.

4. Why doesn't Gauss Law work for point charges?

Gauss Law is not applicable to point charges because it assumes a continuous charge distribution. Point charges have no dimensions and cannot be treated as a continuous distribution of charge. Instead, Coulomb's Law is used to calculate the electric field due to a point charge.

5. Can Gauss Law be used for any shape of closed surface?

Yes, Gauss Law can be used for any shape of closed surface. As long as the electric field is constant and parallel to the surface at every point, the net electric flux through the surface can be calculated using Gauss Law. This makes it a versatile tool for analyzing electric fields in various shapes and configurations.

Similar threads

Feb 12, 2022
May 21, 2018
Oct 3, 2018
Jan 31, 2018
Sep 24, 2018
Jan 26, 2018
Dec 16, 2017
Feb 16, 2016
Oct 4, 2018

Hot Threads

Formula derivation connecting vertical water flowrate & horizontal distance moved by a suspended sphere
Current through a circuit when the key is open
Understanding Inductance and Induced EMF in Simple Circuits
Small oscillations of a simple pendulum placed on a moving block
Two concentric conducting spherical shells and resistor in between

Recent Insights

Insights Aspects Behind the Concept of Dimension in Various Fields
Insights Views On Complex Numbers
Insights Addition of Velocities (Velocity Composition) in Special Relativity
Insights Schrödinger’s Cat and the Qbit
Insights The Slinky Drop Experiment Analysed
Insights How to Solve a Multi-Atwood Machine Assembly

Physics Class-12th Notes
Physics Formulas
Physics Symbol
Application of Physics
Class 8 Science
Class 9 Science
Class 10 Science
Class 11 Science
Class 12 Science
Class 8 Study Material
Class 9 Study Material
Class 10 Study Material
Class 11 Study Material
Class 12 Study Material
CBSE Class 12 Physics Notes 2023-24

Chapter 1 - ELECTRIC CHARGES AND FIELDS

Electric Charge and Electric Field
Electric Charge
Conductors and Insulators
Basic Properties of Electric Charge
Coulomb's Law
Forces Between Multiple Charges
Electric Field
Electric Field Lines
What is Electric Flux?
Electric Dipole
Continuous Charge Distribution
Applications of Gauss's Law

Chapter 2 - ELECTROSTATIC POTENTIAL AND CAPACITANCE

Electric Potential Energy
Electric Potential Due to a Point Charge
Electric Potential Of A Dipole and System Of Charges
Equipotential Surfaces
Potential Energy of a System of Charges
Potential Energy in an External Field
Electrostatics of Conductors
Dielectrics and Polarisation
Capacitor and Capacitance
What is a Parallel Plate Capacitor?
Capacitors in Series and Parallel
Energy stored in a Capacitor

Chapter 3 - CURRENT ELECTRICITY

Electric Current
Electric Current in Conductors
Ohm's Law - Definition, Formula, Applications, Limitations
Drift Velocity
Limitations of Ohm's Law
Resistivity
Temperature Dependence of Resistance
Electrical Energy and Power
Electromotive Force
Combination of Cells in Series and Parallel
Kirchhoff's Laws
Wheatstone Bridge

Chapter 4 - MOVING CHARGES AND MAGNETISM

Magnetic Force on a Current carrying Wire
Motion of a Charged Particle in a Magnetic Field
Biot-Savart Law
Magnetic Field on the Axis of a Circular Current Loop
Ampere's Circuital Law and Problems on It
Force between Two Parallel Current Carrying Conductors
Current Loop as a Magnetic Dipole
Moving Coil Galvanometer

Chapter 5 - MAGNETISM AND MATTER

Gauss's Law
Magnetization and Magnetic Intensity

CHAPTER 6 - ELECTROMAGNETIC INDUCTION

Experiments of Faraday and Henry
Magnetic Flux
Faraday’s Laws of Electromagnetic Induction
Motional Electromotive Force
Inductance - Definition, Derivation, Types, Examples
AC Generator - Principle, Construction, Working, Applications

CHAPTER 7 - ALTERNATING CURRENT

AC Voltage Applied to a Resistor
Phasors | Definition, Examples & Diagram
AC Voltage Applied to an Inductor
AC Voltage Applied to a Capacitor
Series LCR Circuits
Power Factor in AC circuit
Transformer

CHAPTER 8 - ELECTROMAGNETIC WAVES

Displacement Current
Electromagnetic Waves
Electromagnetic Spectrum

CHAPTER 9 - RAY OPTICS AND OPTICAL INSTRUMENTS

Spherical Mirrors
Refraction of Light
Total Internal Reflection
Image formation by Spherical Lenses
Dispersion of Light through a Prism

CHAPTER 10 - WAVE OPTICS

Huygen's Wave Theory
Young's Double Slit Experiment
Diffraction of light
Polarization of Light

CHAPTER 11 - DUAL NATURE OF RADIATION AND MATTER

Photoelectric Effect
Experimental Study of Photoelectric Effect
Einstein's Photoelectric Equation
Wave Nature of Matter and De Broglie’s Equation

CHAPTER 12 ATOMS

What is Atom?
Alpha Particle Scattering and Rutherford's Nuclear Model of Atom
Atomic Spectra
Bohr's Model of the Hydrogen Atom
Spectrum of the Hydrogen Atom

CHAPTER 13 NUCLEI

Nucleus: Structure and Function
Structure of Nucleus
Size of The Nucleus - Rutherford Gold Foil Experiment
Nuclear Binding Energy - Definition, Formula, Examples
Nuclear Force
Radioactivity - Definition, Laws, Occurrence, Applications
Nuclear Energy - Definition, Types, Applications

CHAPTER 14 - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS

Semiconductors
What is Intrinsic Semiconductor ?
Extrinsic Semiconductor
PN Junction Diode
CBSE Class 12 Previous Year Question Papers

Gauss’s Law

Gauss law is defined as the total flux out of the closed surface is equal to the flux enclosed by the surface divided by the permittivity. The Gauss Law, which analyses electric charge, a surface, and the issue of electric flux, is analyzed. Let us learn more about the law and how it functions so that we may comprehend the equation of the law.

What is Gauss Law?

According to gauss law, the total electric flux out of a closed surface is equal to the charge contained divided by the permittivity. The electric flux in a given area is calculated by multiplying the electric field by the area of the surface projected in a plane perpendicular to the field. The total flux associated with a closed surface equals 1 ⁄ ε 0 times the charge encompassed by the closed surface, according to the Gauss law.

∮ E.ds = q ⁄ ε o

For example, a point charge ‘q’ is put within a cube with the edge ‘a’. The flux across each face of the cube is now q ⁄ 6ε o , according to Gauss law. The electric field is the most fundamental concept in understanding electricity. In general, the electric field of a surface is computed using Coulomb’s law ; however, understanding the idea of Gauss’ law is required to calculate the electric field distribution in a closed surface. It describes how an electric charge is enclosed in a closed surface or how an electric charge is present in a closed surface that is enclosed.

Gauss Law Formula

According to the Gauss law formula, the total electric charge enclosed in a closed surface is proportional to the total flux enclosed by the surface. As a consequence, the total electric charge Q contained by the surface is: if ε 0 is electric constant and ϕ is total flux.

Q = ϕ ε o The formula of Gauss law is given by: ϕ = Q⁄ε o Where, ε o is electrostatic constant, Q is total charge within a given surface, and ϕ is flux enclosed by surface.

The Gauss Theorem

The Gauss theorem connects the ‘flow’ of electric field lines (flux) to the charges within the enclosed surface in simple terms. The net charge in the volume contained by a closed surface is exactly proportional to the net flux through the closed surface.

ϕ = E.dA = q net ⁄ ε o

The net electric flow stays 0 if no charges are contained by a surface. The number of electric field lines entering the surface equals the number of field lines exiting the surface.

A corollary of the gauss theorem statement:

The electric flux from any closed surface is only due to the sources and sinks of electric fields enclosed by the surface. The electric flux is unaffected by any charges outside the surface. Furthermore, only electric charges may operate as electric field sources or sinks. It is important to note that changing magnetic field cannot act as electric field sources or sinks.

As it encloses a net charge, the net flow for the surface on the left is non-zero. Because the right-hand surface does not contain any charge, the net flow is zero. The Gauss law is nothing more than a repetition of Coulomb’s law. Coulomb’s law is readily obtained by applying the Gauss theorem to a point charge surrounded by a sphere.

Note: Gauss’ law and Coulomb’s law are closely related. If gauss law is applied to a point charge in a sphere, it will be the same as applying coulomb’s law.

Gauss Law Equation

Gauss law equation can be understood using an integral equation. Gauss’s law in integral form is mentioned below:

∫E.dA = Q/ε 0 ⇢ (1) Where, E is the electric field Q is the electric charge enclosed ε 0 is the electric permittivity of free space A is the outward pointing normal area vector

Flux is a measure of the strength of a field passing through a surface. Electric flux is given as:

Φ = ∫E⋅dA ⇢ (2)

Application of Gauss Law

There are different formulae obtained from the application of Gauss law for different conditions. Below are some well-known applications of Gauss law :

In a medium with a dielectric constant of K, the strength of the electric field near a plane-charged conductor E = σ ⁄ K ε o . E air = σ ⁄ ε o when the dielectric medium is air.
At a distance of ‘r’ in the case of an infinite charge line, E = (1 ⁄ 4 × π r ε 0 ) (2π ⁄ r) = λ ⁄ 2π r ε o , where λ is linear charge density.
In a condenser or capacitor, the field between two parallel plates is E = σ ⁄ ε 0 , where σ is the surface charge density.
The electric field strength near a plane sheet of charge is E = σ ⁄ 2K ε o , where σ is the surface charge density .

$E = \frac{1}{4\pi\epsilon_o}\frac{qx}{(R^2 + x^2)^{3/2}}$

Gauss Law Derivation – Electric Field due to Infinite Wire

To find the electric field due to an infinite wire , assume the charge per unit on the infinitely long wire is λ. The electric field is radially away from all points of the wire, and no component is parallel to the line of charge. Now, assume the wire as a cylinder (with radius ‘r’ and length ‘l’) centered on the line of charge as the gaussian surface.

The electric field is perpendicular to the cylinder. Hence, the angle between the electric field and area vector is 0°. So, cosθ = 1. The top and bottom of the cylinder are parallel to the electric field. Hence, the area vector here is 90° w.r.t. the electric field. Therefore, cosθ = 0. Hence, we can say that the electric flux occurs only due to the curved surface of the cylinder. According to gauss law:

ϕ = E.d ⇢ A

ϕ net = ϕ curved + ϕ top + ϕ bottom

ϕ = E.d ⇢ A = ∫E.dA cos0 + ∫E.dA cos90 + ∫E.dA cos90

The curved surface is equidistant from the line of charge due to its radial symmetry. So, the electric field on the surface has a constant value throughout the surface.

ϕ = ∫E.dA = ∫E. 2πrl

The net charge enclosed by the surface:

q net = λ.l

Now, using gauss theorem:

ϕ = ∫E. 2πrl = q net ⁄ ε o = λ.l/ε o

∫E. 2πrl = λ.l/ε o

E = λ/2πrε o

Solved Examples on Gauss Law

Example 1: In the x-direction, there is a homogeneous electric field of size E = 50 N⁄C. Calculate the flux of this field across a plane square area with an edge of 5 cm in the y-z plane using the Gauss theorem. Assume that the normal is positive along the positive x-axis.

Given: Electric field, E = 50 N⁄C Edge length of square, a = 5 cm = 0.05 m The flux of the field across a plane square, ϕ = ∫ E cosθ ds As the normal to the area points along the electric field, θ = 0. Also, E is uniform so, Φ = E ΔS = (50 N⁄C) (0.05 m) 2 = 0.125 N m 2 C -1 . Hence, the flux of the given field is 0.125 N m 2 C -1 .

Example 2: There are three charges, q 1 , q 2 , and q 3, having charges 4 C, 7 C, and 2 C enclosed in a surface. Find the total flux enclosed by the surface.

Total charge Q, Q = q 1 + q 2 + q 3 = 4 C + 7 C + 2 C = 13 C The total flux, ϕ = Q ⁄ ε 0 ϕ = 13 C ⁄ (8.854×10 −12 F ⁄ m) ϕ = 1.468 N m 2 C -1 Therefore, the total flux enclosed by the surface is 1.584 N m 2 C -1 .

Example 3: Two conducting plates having charges Q 1 and Q 2 , are kept parallel to each other. Find the distribution on all four surfaces.

It can be seen from the figure that two faces lie inside the conductor when E = 0. The flux is also 0. The faces that are outside are parallel to the electric field, the flux there will be 0 too. Therefore, the total flux of the electric field is 0. From gauss law, the total charge inside the closed surface must be 0. Therefore, the charge on the inner side of one plate should be equal to the charge on the other side. Using the equation E = σ/2ε 0 , the electric field at P: Due to the charge Q 1 – q = (Q 1 – q)/2Aε 0 (downward). Due to the charge +q = +q/ε 0 (upward). Due to the charge Q 2 + q = (Q 2 + q)/2Aε 0 (upward) Due to the charge -q = -q/ε 0 (downward). The net electric field is in the downward direction: (Q 1 – q)/2Aε 0 + (-q/ε 0 ) + (Q 2 + q)/2Aε 0 + +q/ε 0 Q 1 -q +q -Q 2 = 0 q = (Q 1 – Q 2 )/2 Q 1 – q = (Q 1 + Q 2 )/2 Q 2 + q = (Q 1 + Q 2 )/2

Example 4: What is the differential form of the Gauss theorem?

The electric field is related to the charge distribution at a certain location in space by the differential version of Gauss law. To clarify, according to the law, the electric field’s divergence (E) is equal to the volume charge density (ρ) at a given position. It’s written like this: ΔE = ρ ⁄ ε 0 Here, ε 0 is the permittivity of free space.

Example 5: There are three concentric spherical shells A, B, and C with radii a, b, and c. The charges are present on shells A and C (q and -q respectively), and shell B is earthed. Find the total charges appearing on B and C.

Since the inner surface of shell B must have a charge of -q, suppose the outer surface of B has a charge ‘x’. Then, the inner surface of C must have a charge of ‘-x’. Potential due to charge ‘q’ on A = q/4πε 0 b Potential due to ‘-q’ on inner surface of B = -q/4πε 0 b Potential due to ‘x’ on outer surface of B = x/4πε 0 b Potential due to ‘-x’ on inner surface of C = -x/4πε 0 c Potential due to ‘x – q’ on inner surface of C = x – q/4πε 0 c Now, the net potential: VB = x/4πε 0 b – q/4πε 0 c This potential is equated to 0 as the shell B is earthed. Therefore, x = qb/c Below is the figure showing the charges on each surface:

FAQs on Gauss Law

Question 1: State Gauss law.

Gauss law states that the net flux of an electric field is directly proportional to the charge enclosed in a closed surface.

Question 2: How do we choose an appropriate Gaussian Surface for different cases?

In order to select an acceptable Gaussian Surface, we must consider the fact that the charge-to-dielectric constant ratio is supplied by a (two-dimensional) surface integral over the charge distribution’s electric field symmetry. We’ll need to know about three potential scenarios. When the charge distribution is spherically symmetric, it is called spherical. When the charge distribution is cylindrically symmetric, it is called cylindrical. When the charge distribution exhibits translational symmetry along a plane, it is called a pillbox. Depending on where we want to compute the field, we may determine the size of the surface. The Gauss theorem is useful for determining the direction of a field when there is symmetry, as it informs us how the field is directed.

Question 3: State gauss law in electrostatics.

Gauss law in electrostatics states that the electric flux through any closed surface is equal to the net charge enclosed by the surface divided by the permittivity of free space.Normally, the Gauss law is employed to calculate the electric field of symmetric charge distributions. When using this law to solve the problem of the electric field, there are numerous processes required. The following are the details: First, we must determine the charge distribution’s spatial symmetry. The next step is to select a proper Gaussian surface that has the same symmetry as the charge distribution. Its ramifications must also be determined. Calculate the flux across the surface by evaluating the integral ϕ s E over the Gaussian surface. Calculate the amount of charge contained within the Gaussian surface. Calculate the charge distribution’s electric field. However, in order to determine the electric field, pupils must remember the three forms of symmetry. The following are the several forms of symmetry: Symmetry on a sphere Symmetry in a cylindrical shape Symmetry on a plane

Question 4: What are the applications of Gauss law?

Complex electrostatic problems involving symmetry like cylindrical, spherical, etc. can be solved using Gauss law. It also helps solving for the electric field that involves complex calculations.

Question 5: What is Gaussian surface?

Gaussian surface is the surface through which electric flux is calculated.

Question 6: State Gauss law for magnetism.

Gauss law for magnetism states that the magnetic flux across any closed surface is 0. This can be written as Div. B = 0, where Div. B is the divergence factor of B.

Gauss’s Law is a fundamental principle in physics that relates the electric field to the distribution of electric charges. It states that the total electric flux through any closed surface is equal to the total charge enclosed by the surface divided by the permittivity of free space (ε0). Mathematically, Gauss’s Law can be expressed as:

∮S E · dA = Qenc/ε0

where ∮S represents the surface integral over a closed surface S, E is the electric field vector, dA is the surface area vector, Qenc is the total charge enclosed by the surface, and ε0 is the permittivity of free space.

Gauss’s Law is a powerful tool for calculating electric fields in situations where the symmetry of the charge distribution makes it difficult to use Coulomb’s Law. By using Gauss’s Law, it is possible to calculate the electric field of a uniformly charged sphere, cylinder, or plane, for example.

Gauss’s Law has important applications in many areas of physics, including electromagnetism, electrostatics, and quantum mechanics. It is used to analyze the behavior of electric fields in charged particles, capacitors, and other electrical devices. It also plays a key role in the understanding of electromagnetic radiation and the propagation of radio waves.

Electropotential Surface Electric potential and potential difference Electric Potential Energy

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

MEMBERSHIP PROGRAMS

Law.com Pro
Law.com Pro Mid-Market
Global Leaders In Law
Global Leaders In Law Advisers
Private Client Global Elite

MEDIA BRANDS

Law.com Radar

American Lawyer

Corporate Counsel
National Law Journal
Legal Tech News
New York Law Journal
The Legal Intelligencer
The Recorder
Connecticut Law Tribune
Daily Business Review
Daily Report
Delaware Business Court Insider
Delaware Law Weekly

New Jersey Law Journal

Texas Lawyer
Supreme Court Brief
Litigation Daily
Deals & Transactions

Law Firm Management

Legal Practice Management
Legal Technology
Intellectual Property
Cybersecurity
Law Journal Newsletters
Analyst Reports
Diversity Scorecard
Kirkland & Ellis
Latham & Watkins
Baker McKenzie
Verdict Search
Law.com Compass
China Law & Practice
Insurance Coverage Law Center
Law Journal Press
Lean Adviser Legal
Legal Dictionary
Law Catalog
Expert Witness Search
Recruiters Directory
Editorial Calendar

Legal Newswire

Lawyer Pages
Law Schools
Women in Influence (WIPL)
GC Profiles
How I Made It
Instant Insights
Special Reports
Resource Center
LMA Member Benefits
Legal Leaders
Trailblazers
Expert Perspectives
Lawjobs.com
Book Center
Professional Announcements
Asset & Logo Licensing

Content Source

Content Type

About Us | Contact Us | Site Map

Advertise | Customer Service | Terms of Service

FAQ | Privacy Policy

Business of Law News (current)
Surveys & Rankings Amlaw 100 Amlaw 200 Diversity Scorecard A-List Pro Bono Report Mid-Level Associates Browse All ›
Litigation Daily (current)
Law.com Radar (current)

The Fastest Growing Am Law 200 Firm Over the Last 5 Years

A look at the firm's growth and strategy is a case study on how a law firm can add market share, climb the rankings, and grow profits, all at the same time.

July 01, 2024 at 05:00 AM

6 minute read

Andrew Maloney

Share with email, thank you for sharing, what you need to know.

Since 2018, Spencer Fane has grown from 243 lawyers to about 419 and gone from 15 offices in 8 states to 26 offices in 14 states and the District of Columbia.
The firm's chair said he and his partners are 'agnostic' about growth, though Spencer Fane has done a little bit of everything to expand their reach and add talent.

The fastest-growing Am Law 200 firm by revenue over the last half-decade isn’t necessarily who you’d expect.

Spencer Fane, once a regional firm mostly known in the Midwest, has leapfrogged 21 spots in the Am Law 200 rankings in the last two years to No. 142 this year, generating $266.8 million in 2023. Overall, the Kansas City-founded firm has increased revenue by roughly 139% since 2018, the highest growth percentage of any Am Law 200 firm in the span of time, including among the New York and West Coast elite firms.

Want to continue reading? Become an ALM Digital Reader for Free!

Benefits of a digital membership.

Free access to 1 article* every 30 days
Access to the entire ALM network of websites
Unlimited access to the ALM suite of newsletters
Build custom alerts on any search topic of your choosing
Search by a wide range of topics

Already have an account? Sign In Now

*May exclude premium content

You Might Like

Taft Stettinius & Hollister Continues Expansion With 6 Lawyers From Ice Miller

By Alexander Lugo

Cooley Continues Bankruptcy Expansion With Gibson Dunn Partner Hire

California Law Firms Broaden Intellectual Property Ranks With New Partner Hires

By Samson Amore

Big Law Leader: 'Stay True to Foundational Principles'

By Richard A. Rosenbaum

Law Firms Mentioned

Spencer Fane Britt & Browne

Featured Firms

Law Offices of Gary Martin Hays & Associates P.C. 75 Ponce De Leon Ave NE Ste 101 Atlanta , GA 30308 (470) 294-1674 www.garymartinhays.com

Law Offices of Mark E. Salomone 2 Oliver St #608 Boston , MA 02109 (857) 444-6468 www.marksalomone.com

Smith & Hassler 1225 N Loop W #525 Houston , TX 77008 (713) 739-1250 www.smithandhassler.com

Presented by BigVoodoo

Subscribe to The American Lawyer

Don't miss the crucial news and insights you need to make informed legal decisions. Join The American Lawyer now!

Already have an account? Sign In

The American Lawyer provides the most informed and trusted source of news, data, analysis and forecasting on the global business of law.

Latest stories

Surveys & Rankings

Pro Bono Report

Special Packages

Special Supplements
Current Issue

Human Subjects Office

Medical terms in lay language.

Please use these descriptions in place of medical jargon in consent documents, recruitment materials and other study documents. Note: These terms are not the only acceptable plain language alternatives for these vocabulary words.

This glossary of terms is derived from a list copyrighted by the University of Kentucky, Office of Research Integrity (1990).

For clinical research-specific definitions, see also the Clinical Research Glossary developed by the Multi-Regional Clinical Trials (MRCT) Center of Brigham and Women’s Hospital and Harvard and the Clinical Data Interchange Standards Consortium (CDISC) .

Alternative Lay Language for Medical Terms for use in Informed Consent Documents

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

ABDOMEN/ABDOMINAL body cavity below diaphragm that contains stomach, intestines, liver and other organs ABSORB take up fluids, take in ACIDOSIS condition when blood contains more acid than normal ACUITY clearness, keenness, esp. of vision and airways ACUTE new, recent, sudden, urgent ADENOPATHY swollen lymph nodes (glands) ADJUVANT helpful, assisting, aiding, supportive ADJUVANT TREATMENT added treatment (usually to a standard treatment) ANTIBIOTIC drug that kills bacteria and other germs ANTIMICROBIAL drug that kills bacteria and other germs ANTIRETROVIRAL drug that works against the growth of certain viruses ADVERSE EFFECT side effect, bad reaction, unwanted response ALLERGIC REACTION rash, hives, swelling, trouble breathing AMBULATE/AMBULATION/AMBULATORY walk, able to walk ANAPHYLAXIS serious, potentially life-threatening allergic reaction ANEMIA decreased red blood cells; low red cell blood count ANESTHETIC a drug or agent used to decrease the feeling of pain, or eliminate the feeling of pain by putting you to sleep ANGINA pain resulting from not enough blood flowing to the heart ANGINA PECTORIS pain resulting from not enough blood flowing to the heart ANOREXIA disorder in which person will not eat; lack of appetite ANTECUBITAL related to the inner side of the forearm ANTIBODY protein made in the body in response to foreign substance ANTICONVULSANT drug used to prevent seizures ANTILIPEMIC a drug that lowers fat levels in the blood ANTITUSSIVE a drug used to relieve coughing ARRHYTHMIA abnormal heartbeat; any change from the normal heartbeat ASPIRATION fluid entering the lungs, such as after vomiting ASSAY lab test ASSESS to learn about, measure, evaluate, look at ASTHMA lung disease associated with tightening of air passages, making breathing difficult ASYMPTOMATIC without symptoms AXILLA armpit

BENIGN not malignant, without serious consequences BID twice a day BINDING/BOUND carried by, to make stick together, transported BIOAVAILABILITY the extent to which a drug or other substance becomes available to the body BLOOD PROFILE series of blood tests BOLUS a large amount given all at once BONE MASS the amount of calcium and other minerals in a given amount of bone BRADYARRHYTHMIAS slow, irregular heartbeats BRADYCARDIA slow heartbeat BRONCHOSPASM breathing distress caused by narrowing of the airways

CARCINOGENIC cancer-causing CARCINOMA type of cancer CARDIAC related to the heart CARDIOVERSION return to normal heartbeat by electric shock CATHETER a tube for withdrawing or giving fluids CATHETER a tube placed near the spinal cord and used for anesthesia (indwelling epidural) during surgery CENTRAL NERVOUS SYSTEM (CNS) brain and spinal cord CEREBRAL TRAUMA damage to the brain CESSATION stopping CHD coronary heart disease CHEMOTHERAPY treatment of disease, usually cancer, by chemical agents CHRONIC continuing for a long time, ongoing CLINICAL pertaining to medical care CLINICAL TRIAL an experiment involving human subjects COMA unconscious state COMPLETE RESPONSE total disappearance of disease CONGENITAL present before birth CONJUNCTIVITIS redness and irritation of the thin membrane that covers the eye CONSOLIDATION PHASE treatment phase intended to make a remission permanent (follows induction phase) CONTROLLED TRIAL research study in which the experimental treatment or procedure is compared to a standard (control) treatment or procedure COOPERATIVE GROUP association of multiple institutions to perform clinical trials CORONARY related to the blood vessels that supply the heart, or to the heart itself CT SCAN (CAT) computerized series of x-rays (computerized tomography) CULTURE test for infection, or for organisms that could cause infection CUMULATIVE added together from the beginning CUTANEOUS relating to the skin CVA stroke (cerebrovascular accident)

DERMATOLOGIC pertaining to the skin DIASTOLIC lower number in a blood pressure reading DISTAL toward the end, away from the center of the body DIURETIC "water pill" or drug that causes increase in urination DOPPLER device using sound waves to diagnose or test DOUBLE BLIND study in which neither investigators nor subjects know what drug or treatment the subject is receiving DYSFUNCTION state of improper function DYSPLASIA abnormal cells

ECHOCARDIOGRAM sound wave test of the heart EDEMA excess fluid collecting in tissue EEG electric brain wave tracing (electroencephalogram) EFFICACY effectiveness ELECTROCARDIOGRAM electrical tracing of the heartbeat (ECG or EKG) ELECTROLYTE IMBALANCE an imbalance of minerals in the blood EMESIS vomiting EMPIRIC based on experience ENDOSCOPIC EXAMINATION viewing an internal part of the body with a lighted tube ENTERAL by way of the intestines EPIDURAL outside the spinal cord ERADICATE get rid of (such as disease) Page 2 of 7 EVALUATED, ASSESSED examined for a medical condition EXPEDITED REVIEW rapid review of a protocol by the IRB Chair without full committee approval, permitted with certain low-risk research studies EXTERNAL outside the body EXTRAVASATE to leak outside of a planned area, such as out of a blood vessel

FDA U.S. Food and Drug Administration, the branch of federal government that approves new drugs FIBROUS having many fibers, such as scar tissue FIBRILLATION irregular beat of the heart or other muscle

GENERAL ANESTHESIA pain prevention by giving drugs to cause loss of consciousness, as during surgery GESTATIONAL pertaining to pregnancy

HEMATOCRIT amount of red blood cells in the blood HEMATOMA a bruise, a black and blue mark HEMODYNAMIC MEASURING blood flow HEMOLYSIS breakdown in red blood cells HEPARIN LOCK needle placed in the arm with blood thinner to keep the blood from clotting HEPATOMA cancer or tumor of the liver HERITABLE DISEASE can be transmitted to one’s offspring, resulting in damage to future children HISTOPATHOLOGIC pertaining to the disease status of body tissues or cells HOLTER MONITOR a portable machine for recording heart beats HYPERCALCEMIA high blood calcium level HYPERKALEMIA high blood potassium level HYPERNATREMIA high blood sodium level HYPERTENSION high blood pressure HYPOCALCEMIA low blood calcium level HYPOKALEMIA low blood potassium level HYPONATREMIA low blood sodium level HYPOTENSION low blood pressure HYPOXEMIA a decrease of oxygen in the blood HYPOXIA a decrease of oxygen reaching body tissues HYSTERECTOMY surgical removal of the uterus, ovaries (female sex glands), or both uterus and ovaries

IATROGENIC caused by a physician or by treatment IDE investigational device exemption, the license to test an unapproved new medical device IDIOPATHIC of unknown cause IMMUNITY defense against, protection from IMMUNOGLOBIN a protein that makes antibodies IMMUNOSUPPRESSIVE drug which works against the body's immune (protective) response, often used in transplantation and diseases caused by immune system malfunction IMMUNOTHERAPY giving of drugs to help the body's immune (protective) system; usually used to destroy cancer cells IMPAIRED FUNCTION abnormal function IMPLANTED placed in the body IND investigational new drug, the license to test an unapproved new drug INDUCTION PHASE beginning phase or stage of a treatment INDURATION hardening INDWELLING remaining in a given location, such as a catheter INFARCT death of tissue due to lack of blood supply INFECTIOUS DISEASE transmitted from one person to the next INFLAMMATION swelling that is generally painful, red, and warm INFUSION slow injection of a substance into the body, usually into the blood by means of a catheter INGESTION eating; taking by mouth INTERFERON drug which acts against viruses; antiviral agent INTERMITTENT occurring (regularly or irregularly) between two time points; repeatedly stopping, then starting again INTERNAL within the body INTERIOR inside of the body INTRAMUSCULAR into the muscle; within the muscle INTRAPERITONEAL into the abdominal cavity INTRATHECAL into the spinal fluid INTRAVENOUS (IV) through the vein INTRAVESICAL in the bladder INTUBATE the placement of a tube into the airway INVASIVE PROCEDURE puncturing, opening, or cutting the skin INVESTIGATIONAL NEW DRUG (IND) a new drug that has not been approved by the FDA INVESTIGATIONAL METHOD a treatment method which has not been proven to be beneficial or has not been accepted as standard care ISCHEMIA decreased oxygen in a tissue (usually because of decreased blood flow)

LAPAROTOMY surgical procedure in which an incision is made in the abdominal wall to enable a doctor to look at the organs inside LESION wound or injury; a diseased patch of skin LETHARGY sleepiness, tiredness LEUKOPENIA low white blood cell count LIPID fat LIPID CONTENT fat content in the blood LIPID PROFILE (PANEL) fat and cholesterol levels in the blood LOCAL ANESTHESIA creation of insensitivity to pain in a small, local area of the body, usually by injection of numbing drugs LOCALIZED restricted to one area, limited to one area LUMEN the cavity of an organ or tube (e.g., blood vessel) LYMPHANGIOGRAPHY an x-ray of the lymph nodes or tissues after injecting dye into lymph vessels (e.g., in feet) LYMPHOCYTE a type of white blood cell important in immunity (protection) against infection LYMPHOMA a cancer of the lymph nodes (or tissues)

MALAISE a vague feeling of bodily discomfort, feeling badly MALFUNCTION condition in which something is not functioning properly MALIGNANCY cancer or other progressively enlarging and spreading tumor, usually fatal if not successfully treated MEDULLABLASTOMA a type of brain tumor MEGALOBLASTOSIS change in red blood cells METABOLIZE process of breaking down substances in the cells to obtain energy METASTASIS spread of cancer cells from one part of the body to another METRONIDAZOLE drug used to treat infections caused by parasites (invading organisms that take up living in the body) or other causes of anaerobic infection (not requiring oxygen to survive) MI myocardial infarction, heart attack MINIMAL slight MINIMIZE reduce as much as possible Page 4 of 7 MONITOR check on; keep track of; watch carefully MOBILITY ease of movement MORBIDITY undesired result or complication MORTALITY death MOTILITY the ability to move MRI magnetic resonance imaging, diagnostic pictures of the inside of the body, created using magnetic rather than x-ray energy MUCOSA, MUCOUS MEMBRANE moist lining of digestive, respiratory, reproductive, and urinary tracts MYALGIA muscle aches MYOCARDIAL pertaining to the heart muscle MYOCARDIAL INFARCTION heart attack

NASOGASTRIC TUBE placed in the nose, reaching to the stomach NCI the National Cancer Institute NECROSIS death of tissue NEOPLASIA/NEOPLASM tumor, may be benign or malignant NEUROBLASTOMA a cancer of nerve tissue NEUROLOGICAL pertaining to the nervous system NEUTROPENIA decrease in the main part of the white blood cells NIH the National Institutes of Health NONINVASIVE not breaking, cutting, or entering the skin NOSOCOMIAL acquired in the hospital

OCCLUSION closing; blockage; obstruction ONCOLOGY the study of tumors or cancer OPHTHALMIC pertaining to the eye OPTIMAL best, most favorable or desirable ORAL ADMINISTRATION by mouth ORTHOPEDIC pertaining to the bones OSTEOPETROSIS rare bone disorder characterized by dense bone OSTEOPOROSIS softening of the bones OVARIES female sex glands

PARENTERAL given by injection PATENCY condition of being open PATHOGENESIS development of a disease or unhealthy condition PERCUTANEOUS through the skin PERIPHERAL not central PER OS (PO) by mouth PHARMACOKINETICS the study of the way the body absorbs, distributes, and gets rid of a drug PHASE I first phase of study of a new drug in humans to determine action, safety, and proper dosing PHASE II second phase of study of a new drug in humans, intended to gather information about safety and effectiveness of the drug for certain uses PHASE III large-scale studies to confirm and expand information on safety and effectiveness of new drug for certain uses, and to study common side effects PHASE IV studies done after the drug is approved by the FDA, especially to compare it to standard care or to try it for new uses PHLEBITIS irritation or inflammation of the vein PLACEBO an inactive substance; a pill/liquid that contains no medicine PLACEBO EFFECT improvement seen with giving subjects a placebo, though it contains no active drug/treatment PLATELETS small particles in the blood that help with clotting POTENTIAL possible POTENTIATE increase or multiply the effect of a drug or toxin (poison) by giving another drug or toxin at the same time (sometimes an unintentional result) POTENTIATOR an agent that helps another agent work better PRENATAL before birth PROPHYLAXIS a drug given to prevent disease or infection PER OS (PO) by mouth PRN as needed PROGNOSIS outlook, probable outcomes PRONE lying on the stomach PROSPECTIVE STUDY following patients forward in time PROSTHESIS artificial part, most often limbs, such as arms or legs PROTOCOL plan of study PROXIMAL closer to the center of the body, away from the end PULMONARY pertaining to the lungs

QD every day; daily QID four times a day

RADIATION THERAPY x-ray or cobalt treatment RANDOM by chance (like the flip of a coin) RANDOMIZATION chance selection RBC red blood cell RECOMBINANT formation of new combinations of genes RECONSTITUTION putting back together the original parts or elements RECUR happen again REFRACTORY not responding to treatment REGENERATION re-growth of a structure or of lost tissue REGIMEN pattern of giving treatment RELAPSE the return of a disease REMISSION disappearance of evidence of cancer or other disease RENAL pertaining to the kidneys REPLICABLE possible to duplicate RESECT remove or cut out surgically RETROSPECTIVE STUDY looking back over past experience

SARCOMA a type of cancer SEDATIVE a drug to calm or make less anxious SEMINOMA a type of testicular cancer (found in the male sex glands) SEQUENTIALLY in a row, in order SOMNOLENCE sleepiness SPIROMETER an instrument to measure the amount of air taken into and exhaled from the lungs STAGING an evaluation of the extent of the disease STANDARD OF CARE a treatment plan that the majority of the medical community would accept as appropriate STENOSIS narrowing of a duct, tube, or one of the blood vessels in the heart STOMATITIS mouth sores, inflammation of the mouth STRATIFY arrange in groups for analysis of results (e.g., stratify by age, sex, etc.) STUPOR stunned state in which it is difficult to get a response or the attention of the subject SUBCLAVIAN under the collarbone SUBCUTANEOUS under the skin SUPINE lying on the back SUPPORTIVE CARE general medical care aimed at symptoms, not intended to improve or cure underlying disease SYMPTOMATIC having symptoms SYNDROME a condition characterized by a set of symptoms SYSTOLIC top number in blood pressure; pressure during active contraction of the heart

TERATOGENIC capable of causing malformations in a fetus (developing baby still inside the mother’s body) TESTES/TESTICLES male sex glands THROMBOSIS clotting THROMBUS blood clot TID three times a day TITRATION a method for deciding on the strength of a drug or solution; gradually increasing the dose T-LYMPHOCYTES type of white blood cells TOPICAL on the surface TOPICAL ANESTHETIC applied to a certain area of the skin and reducing pain only in the area to which applied TOXICITY side effects or undesirable effects of a drug or treatment TRANSDERMAL through the skin TRANSIENTLY temporarily TRAUMA injury; wound TREADMILL walking machine used to test heart function

UPTAKE absorbing and taking in of a substance by living tissue

VALVULOPLASTY plastic repair of a valve, especially a heart valve VARICES enlarged veins VASOSPASM narrowing of the blood vessels VECTOR a carrier that can transmit disease-causing microorganisms (germs and viruses) VENIPUNCTURE needle stick, blood draw, entering the skin with a needle VERTICAL TRANSMISSION spread of disease

WBC white blood cell

IMAGES

Gauss's law for electric field, Case Study of Gauss's law for electric field, #GaussLaw
Gauss’s Law: Definition, Equations, Problems, and Examples
Gauss`s law
Gauss' Law
Gauss’s Law: Definition, Equations, Problems, and Examples
Gauss' Law: Definition & Examples

VIDEO

12th Physics Numerical Gauss Law
[ 普通物理學-張寶棣 ] 單元18-1: Electric Field and Gauss's Law (1)
GAUSS'S Law of important note for the class 11 #Studypro #jee main
application of gauss law for class 12 CBSE, ISC, UP BOARD ETC
PHYS202 #06: Applications on Gauss' Law
Write Gauss law|| class12 question answer|| #shorts #youtubeshorts

COMMENTS

Case Study Question for Class 12 Physics ...
Case Study Question 5: Surface Charge Density. Surface charge density is defined as the charge per unit surface area the surface (Arial) charge symmetric distribution and follow Gauss law of electro statics mathematical term of surface charge density σ=ΔQ/ΔS. Two large thin metal plates are parallel and close to each other. On their inner ...
6.3: Explaining Gauss's Law
According to Gauss's law, the flux of the electric field E E → through any closed surface, also called a Gaussian surface, is equal to the net charge enclosed (qenc) ( q e n c) divided by the permittivity of free space (ϵ0) ( ϵ 0): ΦClosedSurface = qenc ϵ0. (6.3.4) (6.3.4) Φ C l o s e d S u r f a c e = q e n c ϵ 0.
PDF ApplicationsofGaussLaw
Let S be a sphere of some radius r centered at the origin. By symmetry, the radial electric field is always perpendicular to S, while its magnitude E(r) stays constant along S. This makes S a Gaussian surface, so the flux through S is simply. ΦE[S] = E(r) × A(S) = E(r) × 4πr2. (6) Hence, by Gauss Law, 4πr2.
Worked example: Gauss's law (video)
Video transcript. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
5 Application of Gauss' Law
5-1 Electrostatics is Gauss' law plus …. There are two laws of electrostatics: that the flux of the electric field from a volume is proportional to the charge inside—Gauss' law, and that the circulation of the electric field is zero—$\FLPE$ is a gradient. From these two laws, all the predictions of electrostatics follow.
6.2 Explaining Gauss's Law
Gauss's law generalizes this result to the case of any number of charges and any location of the charges in the space inside the closed surface. According to Gauss's law, the flux of the electric field E → E → through any closed surface, also called a Gaussian surface , is equal to the net charge enclosed ( q enc ) ( q enc ) divided by ...
6.S: Gauss's Law (Summary)
6.3 Explaining Gauss's Law. Gauss's law relates the electric flux through a closed surface to the net charge within that surface, Φ = ∮S E. ⃗. ⋅ n^dA = qenc ε0 Φ = ∮ S E → ⋅ n ^ d A = q e n c ε 0, where qencqenc is the total charge inside the Gaussian surface S. All surfaces that include the same amount of charge have the ...
Gauss Law
⇒ Note: The Gauss law is only a restatement of Coulomb's law. If you apply the Gauss theorem to a point charge enclosed by a sphere, you will get back Coulomb's law easily. Applications of Gauss Law. 1. In the case of a charged ring of radius R on its axis at a distance x from the centre of the ring.
PDF Chapter 4 Gauss's Law
w (Gauss's law) (4.2.5) where qenc is the net charge inside the surface. One way to explain why Gauss's law holds is due to note that the number of field lines that leave the charge is independent of the shape of the imaginary Gaussian surface we choose to enclose the charge. To prove Gauss's law, we introduce the concept of the solid ...
chapte4gauss_law.pdf
This resource includes the following topics: electric flux, Gauss?s law, conductors, force on a conductor, summary, appendix: tensions and pressures, problem-solving strategies, solved problems, conceptual questions, and additional problems.
PDF Gauss's Law
Gauss's Law. Gauss's Law is one of the 4 fundamental laws of electricity and magnetism called Maxwell's Equations. Gauss's law relates charges and electric fields in a subtle and powerful way, but before we can write down Gauss's Law, we need to introduce a new concept: the electric flux through a surface. lines.
17.4: Interpretation of Gauss' Law and vector calculus
Gauss' Law in terms of divergence can be written as: ∇ ⋅ E = ρ ϵ0 (Local version of Gauss' Law) (17.4.1) (17.4.1) ∇ ⋅ E → = ρ ϵ 0 (Local version of Gauss' Law) where ρ ρ is the charge per unit volume at a specific position in space. This is the version of Gauss' Law that is usually seen in advanced textbooks and in Maxwell ...
Gauss's law
The law was first [1] formulated by Joseph-Louis Lagrange in 1773, [2] followed by Carl Friedrich Gauss in 1835, [3] both in the context of the attraction of ellipsoids. It is one of Maxwell's equations, which forms the basis of classical electrodynamics. [note 1] Gauss's law can be used to derive Coulomb's law, [4] and vice versa.
PDF Electric flux, and Gauss' law
verywhere around the sphere!) From Coulomb's law, we know that at the surface of this sphere, E = kQ/R^2 (It's the same in magnitude. to compute r kqΦ =∫ E d, w. ich is thus just ⋅ ∫ dA . R2 But now notice that those are all constants, and c. nstant come out of int. s. So kq Φ = R2 ∫ dA .€Now think what.
Gauss's law
Gauss's law, either of two statements describing electric and magnetic fluxes.Gauss's law for electricity states that the electric flux Φ across any closed surface is proportional to the net electric charge q enclosed by the surface; that is, Φ = q/ε 0, where ε 0 is the electric permittivity of free space and has a value of 8.854 × 10 -12 square coulombs per newton per square metre.
Applications of Gauss's Law
The total electric flux through the Gaussian surface will be. Φ = E × 4 πr 2. Then by Gauss's Law, we can write. Putting the value of surface charge density σ as q/4 πR 2, we can rewrite the electric field as. In vector form, the electric field is. where r is the radius vector, depicting the direction of electric field.
Gauss' Law
Gauss' Law is a law that describes what an electric field will look like due to a known distribution of electric charge. It was first formulated in the 19th century. It was first formulated in the ...
Understanding Gauss's Law: A Comprehensive Guide Class Lectures
This law is named after the German mathematician and physicist Carl Friedrich Gauss, who first formulated it in 1835. Gauss's Law has numerous applications in physics and engineering, including the design of electrical circuits, the analysis of electromagnetic waves, and the study of the behavior of charged particles in electric and magnetic ...
Gauss Law for Magnetic Field, Case Study of Gauss Law for Magnetic
In this video, i have explained Gauss's law for magnetic field with following Outlines:0. Gauss's law 1. Gauss's law for magnetic field2. Basics of Gauss's l...
Gauss's law for electric field, Case Study of Gauss's law for electric
In this video, i have explained Gauss's law for electric field with following Outlines:0. Gauss's law for electric field1. Basics of Gauss's law for electric...
Physics Project On 'Gauss Theorem' For Class 12
Gauss's Law. Gauss's Law, a true heavyweight in the world of electromagnetism, is like the close cousin of Gauss's Theorem. ... In this case, a spherical surface centered on the charge is perfect because it's symmetrical. ... This knowledge is crucial in the study of capacitors and the behavior of dielectric materials. Electric Field ...
Exploring the Limitations of Gauss's Law: A Case Study of a Line Charge
Exploring the Limitations of Gauss's Law: A Case Study of a Line Charge in Air. In summary, the conversation discusses the determination of the electric field at a point (0,10 cm, 0) due to a line charge with a uniform charge density of ρl = 4 (uC/m) along the z-axis between z=0 and z=5 cm. The attempted solution involves using Gauss's law ...
Gauss Law
Note: Gauss' law and Coulomb's law are closely related. If gauss law is applied to a point charge in a sphere, it will be the same as applying coulomb's law. Gauss Law Equation. Gauss law equation can be understood using an integral equation. Gauss's law in integral form is mentioned below: ∫E.dA = Q/ε 0 ⇢ (1) Where, E is the ...
Two members of LEAD presenting at National Science Challenge Webinar
Two members of LEAD presenting at National Science Challenge Webinar, 'Law and Disasters: An Auckland Volcanic Field Case Study' 19 April 2024. APPLY NOW. Are we prepared for disasters? As a nation we have a history of pushing through emergency legislation in the wake of natural hazard events to govern our emergency response. This has led to an ...
The Fastest Growing Am Law 200 Firm Over the Last 5 Years
A look at the firm's growth and strategy is a case study on how a law firm can add market share, climb the rankings, and grow profits, all at the same time. July 01, 2024 at 05:00 AM.
Medical Terms in Lay Language
Human Subjects Office / IRB Hardin Library, Suite 105A 600 Newton Rd Iowa City, IA 52242-1098. Voice: 319-335-6564 Fax: 319-335-7310

Case Study Question for Class 12 Physics Chapter 1 Electric Charges and Fields

Download CBSE Books

6 thoughts on “ Case Study Question for Class 12 Physics Chapter 1 Electric Charges and Fields ”

Leave a Reply Cancel reply

Discover more from Gurukul of Excellence

5 Application of Gauss’ Law

5–1 Electrostatics is Gauss’ law plus …

5–2 Equilibrium in an electrostatic field

5–3 Equilibrium with conductors

5–4 Stability of atoms

5–5 The field of a line charge

5–6 A sheet of charge; two sheets

5–7 A sphere of charge; a spherical shell

5–8 Is the field of a point charge exactly $\boldsymbol{1/r^2}$?

5–9 The fields of a conductor

5–10 The field in a cavity of a conductor

Gauss Law - Applications, Gauss Theorem Formula

JEE Main 2021 LIVE Physics Paper Solutions 24 Feb Shift-1 Memory-based

Table of Content:

Gauss Law Formula

The Gauss Theorem

Applications of Gauss Law

Application of Gauss’s Law – Video Lesson

Electric Field Due to Infinite Wire – Gauss Law Application

Problems on Gauss Law

Gauss’ Law and Conductors – Short Notes for Quick Revision

Gauss Law and Its Applications – Video Lesson

Solved Questions on Gauss Law

How do we choose an appropriate Gaussian surface for different cases?

How is electric flux related to the Gauss law?

What is the differential form of the Gauss theorem?

How to find the electric field using the Gauss law?

Frequently Asked Questions on Gauss Law

Can the Gauss law be applied to the non-uniform electric field?

State the Gauss law.

What is the factor on which the electric field lines depend?

When is the flux through the surface taken as positive or negative?

What is called a Gaussian surface?

Can Coulomb’s law be derived using the Gauss law?

Define surface charge density.

Leave a Comment Cancel reply

Register with Aakash BYJU'S & Download Free PDFs

Browse Course Material

Departments

Learning Resource Types

You are leaving MIT OpenCourseWare

Gauss’s law

Suggested Videos

Browse more Topics under Electric Charges And Fields

Electric Field due to Infinite Wire

Electric Field due to Infinite Plate Sheet

Electric Field due to Thin Spherical Shell

Download Conductors and Insulators Cheat Sheet PDF

Electric Field Outside the Spherical Shell

Electric Field Inside the Spherical Shell

Solved Example for You

Customize your course in 30 seconds

Electric Charges and Fields

Leave a Reply Cancel reply

Download the App

Understanding Gauss's Law: A Comprehensive Guide Class Lectures

Bootcamp Curriculum

Electric Flux

Gauss's Law II

Gauss's Law Example

Uniformly Charged Insulators

Conducting Spherical Shell

What our students say

Join our STEM bootcamps

A free answer just for you

Log in to watch this video ...and 100,000,000 more!

Physics Project On ‘Gauss Theorem’ For Class 12

Acknowledgment

Introduction to Gauss’s Theorem

Gauss’s Law

Cracking the Code of Gauss’s Law:

Closed Surfaces and the Dance of Electric Charges

Closed Surfaces:

Charge Distributions:

Now, let’s connect the dots between these concepts and Gauss’s Law: