

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations
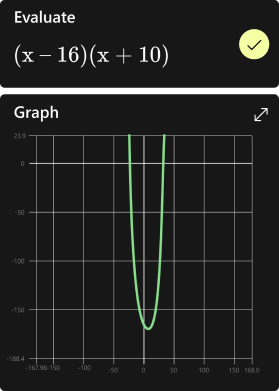
Graph your math problems
Practice, practice, practice

Get math help in your language
- Solve equations and inequalities
- Simplify expressions
- Factor polynomials
- Graph equations and inequalities
- Advanced solvers
- All solvers
- Arithmetics
- Determinant
- Percentages
- Scientific Notation
- Inequalities
What can QuickMath do?
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.
- The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
- The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
- The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
- The calculus section will carry out differentiation as well as definite and indefinite integration.
- The matrices section contains commands for the arithmetic manipulation of matrices.
- The graphs section contains commands for plotting equations and inequalities.
- The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.
Math Topics
More solvers.
- Add Fractions
- Simplify Fractions
Math Solver
Geogebra math solver.
Get accurate solutions and step-by-step explanations for algebra and other math problems, while enhancing your problem-solving skills!

High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Free ready-to-use math resources
Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving
Katie Keeton
Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.
Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.
This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations.
What are problem-solving strategies?
Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies:
- Draw a model
- Use different approaches
- Check the inverse to make sure the answer is correct
Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better.
Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques
Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.
20 Math Strategies For Problem-Solving
Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem.
Here are 20 strategies to help students develop their problem-solving skills.
Strategies to understand the problem
Strategies that help students understand the problem before solving it helps ensure they understand:
- The context
- What the key information is
- How to form a plan to solve it
Following these steps leads students to the correct solution and makes the math word problem easier .
Here are five strategies to help students understand the content of the problem and identify key information.
1. Read the problem aloud
Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.
2. Highlight keywords
When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed. For example, if the word problem asks how many are left, the problem likely requires subtraction. Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.
3. Summarize the information
Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary. Summaries should include only the important information and be in simple terms that help contextualize the problem.
4. Determine the unknown
A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer. Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.
5. Make a plan
Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it. The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer. Encourage students to make a list of each step they need to take to solve the problem before getting started.
Strategies for solving the problem
1. draw a model or diagram.
Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process. It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out
This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives . When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts. The examples below show how 1st-grade students could “act out” an addition and subtraction problem:
| The problem | How to act out the problem |
| Gia has 6 apples. Jordan has 3 apples. How many apples do they have altogether? | Two students use counters to represent the apples. One student has 6 counters and the other student takes 3. Then, they can combine their “apples” and count the total. |
| Michael has 7 pencils. He gives 2 pencils to Sarah. How many pencils does Michael have now? | One student (“Michael”) holds 7 pencils, the other (“Sarah”) holds 2 pencils. The student playing Michael gives 2 pencils to the student playing Sarah. Then the students count how many pencils Michael is left holding. |
3. Work backwards
Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution. This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.
For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71. Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.
4. Write a number sentence
When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved. It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.
5. Use a formula
Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve. Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.
Strategies for checking the solution
Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense.
There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.
Here are five strategies to help students check their solutions.
1. Use the Inverse Operation
For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work.
2. Estimate to check for reasonableness
Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable. Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten. For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10. When the estimate is clear the two numbers are close. This means your answer is reasonable.
3. Plug-In Method
This method is particularly useful for algebraic equations. Specifically when working with variables. To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓
4. Peer Review
Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly. Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills. If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.
5. Use a Calculator
A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.
Step-by-step problem-solving processes for your classroom
In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems.
Polya’s 4 steps include:
- Understand the problem
- Devise a plan
- Carry out the plan
Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall.
Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom.
Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving
Resources .
Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking.
Explore the range of problem solving resources for 2nd to 8th grade students.
One-on-one tutoring
Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards.
Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice.
Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving
Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra.
Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.
READ MORE : 8 Common Core math examples
There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model • act it out • work backwards • write a number sentence • use a formula
Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model • Act it out • Work backwards • Write a number sentence • Use a formula
1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back
Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.
Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms
Ultimate Guide to Metacognition [FREE]
Looking for a summary on metacognition in relation to math teaching and learning?
Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.
Privacy Overview
- Skip to main content
- Skip to primary sidebar
- Skip to footer
Additional menu
Khan Academy Blog
Free Math Worksheets — Over 100k free practice problems on Khan Academy
Looking for free math worksheets.
You’ve found something even better!
That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!
Just choose your grade level or topic to get access to 100% free practice questions:
Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.
- Trigonometry
Statistics and probability
High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.
- Addition and subtraction
- Place value (tens and hundreds)
- Addition and subtraction within 20
- Addition and subtraction within 100
- Addition and subtraction within 1000
- Measurement and data
- Counting and place value
- Measurement and geometry
- Place value
- Measurement, data, and geometry
- Add and subtract within 20
- Add and subtract within 100
- Add and subtract within 1,000
- Money and time
- Measurement
- Intro to multiplication
- 1-digit multiplication
- Addition, subtraction, and estimation
- Intro to division
- Understand fractions
- Equivalent fractions and comparing fractions
- More with multiplication and division
- Arithmetic patterns and problem solving
- Quadrilaterals
- Represent and interpret data
- Multiply by 1-digit numbers
- Multiply by 2-digit numbers
- Factors, multiples and patterns
- Add and subtract fractions
- Multiply fractions
- Understand decimals
- Plane figures
- Measuring angles
- Area and perimeter
- Units of measurement
- Decimal place value
- Add decimals
- Subtract decimals
- Multi-digit multiplication and division
- Divide fractions
- Multiply decimals
- Divide decimals
- Powers of ten
- Coordinate plane
- Algebraic thinking
- Converting units of measure
- Properties of shapes
- Ratios, rates, & percentages
- Arithmetic operations
- Negative numbers
- Properties of numbers
- Variables & expressions
- Equations & inequalities introduction
- Data and statistics
- Negative numbers: addition and subtraction
- Negative numbers: multiplication and division
- Fractions, decimals, & percentages
- Rates & proportional relationships
- Expressions, equations, & inequalities
- Numbers and operations
- Solving equations with one unknown
- Linear equations and functions
- Systems of equations
- Geometric transformations
- Data and modeling
- Volume and surface area
- Pythagorean theorem
- Transformations, congruence, and similarity
- Arithmetic properties
- Factors and multiples
- Reading and interpreting data
- Negative numbers and coordinate plane
- Ratios, rates, proportions
- Equations, expressions, and inequalities
- Exponents, radicals, and scientific notation
- Foundations
- Algebraic expressions
- Linear equations and inequalities
- Graphing lines and slope
- Expressions with exponents
- Quadratics and polynomials
- Equations and geometry
- Algebra foundations
- Solving equations & inequalities
- Working with units
- Linear equations & graphs
- Forms of linear equations
- Inequalities (systems & graphs)
- Absolute value & piecewise functions
- Exponents & radicals
- Exponential growth & decay
- Quadratics: Multiplying & factoring
- Quadratic functions & equations
- Irrational numbers
- Performing transformations
- Transformation properties and proofs
- Right triangles & trigonometry
- Non-right triangles & trigonometry (Advanced)
- Analytic geometry
- Conic sections
- Solid geometry
- Polynomial arithmetic
- Complex numbers
- Polynomial factorization
- Polynomial division
- Polynomial graphs
- Rational exponents and radicals
- Exponential models
- Transformations of functions
- Rational functions
- Trigonometric functions
- Non-right triangles & trigonometry
- Trigonometric equations and identities
- Analyzing categorical data
- Displaying and comparing quantitative data
- Summarizing quantitative data
- Modeling data distributions
- Exploring bivariate numerical data
- Study design
- Probability
- Counting, permutations, and combinations
- Random variables
- Sampling distributions
- Confidence intervals
- Significance tests (hypothesis testing)
- Two-sample inference for the difference between groups
- Inference for categorical data (chi-square tests)
- Advanced regression (inference and transforming)
- Analysis of variance (ANOVA)
- Scatterplots
- Data distributions
- Two-way tables
- Binomial probability
- Normal distributions
- Displaying and describing quantitative data
- Inference comparing two groups or populations
- Chi-square tests for categorical data
- More on regression
- Prepare for the 2020 AP®︎ Statistics Exam
- AP®︎ Statistics Standards mappings
- Polynomials
- Composite functions
- Probability and combinatorics
- Limits and continuity
- Derivatives: definition and basic rules
- Derivatives: chain rule and other advanced topics
- Applications of derivatives
- Analyzing functions
- Parametric equations, polar coordinates, and vector-valued functions
- Applications of integrals
- Differentiation: definition and basic derivative rules
- Differentiation: composite, implicit, and inverse functions
- Contextual applications of differentiation
- Applying derivatives to analyze functions
- Integration and accumulation of change
- Applications of integration
- AP Calculus AB solved free response questions from past exams
- AP®︎ Calculus AB Standards mappings
- Infinite sequences and series
- AP Calculus BC solved exams
- AP®︎ Calculus BC Standards mappings
- Integrals review
- Integration techniques
- Thinking about multivariable functions
- Derivatives of multivariable functions
- Applications of multivariable derivatives
- Integrating multivariable functions
- Green’s, Stokes’, and the divergence theorems
- First order differential equations
- Second order linear equations
- Laplace transform
- Vectors and spaces
- Matrix transformations
- Alternate coordinate systems (bases)
Frequently Asked Questions about Khan Academy and Math Worksheets
Why is khan academy even better than traditional math worksheets.
Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.
| Math Worksheets | Khan Academy |
|---|---|
| Math worksheets take forever to hunt down across the internet | Khan Academy is your one-stop-shop for practice from arithmetic to calculus |
| Math worksheets can vary in quality from site to site | Every Khan Academy question was written by a math expert with a strong education background |
| Math worksheets can have ads or cost money | Khan Academy is a nonprofit whose resources are always free to teachers and learners – no ads, no subscriptions |
| Printing math worksheets use up a significant amount of paper and are hard to distribute during virtual learning | Khan Academy practice requires no paper and can be distributed whether your students are in-person or online |
| Math worksheets can lead to cheating or a lack of differentiation since every student works on the same questions | Khan Academy has a full question bank to draw from, ensuring that each student works on different questions – and at their perfect skill level |
| Math worksheets can slow down student learning since they need to wait for feedback | Khan Academy gives instant feedback after every answer – including hints and video support if students are stuck |
| Math worksheets take up time to collect and take up valuable planning time to grade | Khan Academy questions are graded instantly and automatically for you |
What do Khan Academy’s interactive math worksheets look like?
Here’s an example:
What are teachers saying about Khan Academy’s interactive math worksheets?
“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”
Is Khan Academy free?
Khan Academy’s practice questions are 100% free—with no ads or subscriptions.
What do Khan Academy’s interactive math worksheets cover?
Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.
Is Khan Academy a company?
Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.
Want to get even more out of Khan Academy?
Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.
Get Khanmigo
The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo.
For learners For teachers For parents
Want Better Math Grades?
✅ Unlimited Solutions
✅ Step-by-Step Answers
✅ Available 24/7
➕ Free Bonuses ($1085 value!)
On this page
- Search IntMath
- Math interactives
- About (site info)
- Uses of Trignometry
- ASCIIMath input, KaTeX output
- ASCIIMath input, LaTeX and KaTeX output
- Send Math in emails
- Syntax for ASCIIMathML
- Math Display Experiments
- Scientific Notebook
Math Problem Solver
Related Sections
Math Tutoring
Need help? Chat with a tutor anytime, 24/7.

This tool combines the power of mathematical computation engine that excels at solving mathematical formulas with the power of artificial intelligence large language models to parse and generate natural language answers. This creates a math problem solver that's more accurate than ChatGPT, more flexible than a math calculator, and provides answers faster than a human tutor.
Sign up for free here .
Problem Solver Subjects
Our math problem solver that lets you input a wide variety of math math problems and it will provide a step by step answer. This math solver excels at math word problems as well as a wide range of math subjects.
- Math Word Problems
- Pre-Algebra
- Geometry Graphing
- Trigonometry
- Precalculus
- Finite Math
- Linear Algebra
Here are example math problems within each subject that can be input into the calculator and solved. This list is constanstly growing as functionality is added to the calculator.
Basic Math Solutions
Below are examples of basic math problems that can be solved.
- Long Arithmetic
- Rational Numbers
- Operations with Fractions
- Ratios, Proportions, Percents
- Measurement, Area, and Volume
- Factors, Fractions, and Exponents
- Unit Conversions
- Data Measurement and Statistics
- Points and Line Segments
Math Word Problem Solutions
Math word problems require interpreting what is being asked and simplifying that into a basic math equation. Once you have the equation you can then enter that into the problem solver as a basic math or algebra question to be correctly solved. Below are math word problem examples and their simplified forms.
Word Problem: Rachel has 17 apples. She gives some to Sarah. Sarah now has 8 apples. How many apples did Rachel give her?
Simplified Equation: 17 - x = 8
Word Problem: Rhonda has 12 marbles more than Douglas. Douglas has 6 marbles more than Bertha. Rhonda has twice as many marbles as Bertha has. How many marbles does Douglas have?
Variables: Rhonda's marbles is represented by (r), Douglas' marbles is represented by (d) and Bertha's marbles is represented by (b)
Simplified Equation: {r = d + 12, d = b + 6, r = 2 �� b}
Word Problem: if there are 40 cookies all together and Angela takes 10 and Brett takes 5 how many are left?
Simplified: 40 - 10 - 5
Pre-Algebra Solutions
Below are examples of Pre-Algebra math problems that can be solved.
- Variables, Expressions, and Integers
- Simplifying and Evaluating Expressions
- Solving Equations
- Multi-Step Equations and Inequalities
- Ratios, Proportions, and Percents
- Linear Equations and Inequalities
Algebra Solutions
Below are examples of Algebra math problems that can be solved.
- Algebra Concepts and Expressions
- Points, Lines, and Line Segments
- Simplifying Polynomials
- Factoring Polynomials
- Linear Equations
- Absolute Value Expressions and Equations
- Radical Expressions and Equations
- Systems of Equations
- Quadratic Equations
- Inequalities
- Complex Numbers and Vector Analysis
- Logarithmic Expressions and Equations
- Exponential Expressions and Equations
- Conic Sections
- Vector Spaces
- 3d Coordinate System
- Eigenvalues and Eigenvectors
- Linear Transformations
- Number Sets
- Analytic Geometry
Trigonometry Solutions
Below are examples of Trigonometry math problems that can be solved.
- Algebra Concepts and Expressions Review
- Right Triangle Trigonometry
- Radian Measure and Circular Functions
- Graphing Trigonometric Functions
- Simplifying Trigonometric Expressions
- Verifying Trigonometric Identities
- Solving Trigonometric Equations
- Complex Numbers
- Analytic Geometry in Polar Coordinates
- Exponential and Logarithmic Functions
- Vector Arithmetic
Precalculus Solutions
Below are examples of Precalculus math problems that can be solved.
- Operations on Functions
- Rational Expressions and Equations
- Polynomial and Rational Functions
- Analytic Trigonometry
- Sequences and Series
- Analytic Geometry in Rectangular Coordinates
- Limits and an Introduction to Calculus
Calculus Solutions
Below are examples of Calculus math problems that can be solved.
- Evaluating Limits
- Derivatives
- Applications of Differentiation
- Applications of Integration
- Techniques of Integration
- Parametric Equations and Polar Coordinates
- Differential Equations
Statistics Solutions
Below are examples of Statistics problems that can be solved.
- Algebra Review
- Average Descriptive Statistics
- Dispersion Statistics
- Probability
- Probability Distributions
- Frequency Distribution
- Normal Distributions
- t-Distributions
- Hypothesis Testing
- Estimation and Sample Size
- Correlation and Regression
Finite Math Solutions
Below are examples of Finite Math problems that can be solved.
- Polynomials and Expressions
- Equations and Inequalities
- Linear Functions and Points
- Systems of Linear Equations
- Mathematics of Finance
- Statistical Distributions
Linear Algebra Solutions
Below are examples of Linear Algebra math problems that can be solved.
- Introduction to Matrices
- Linear Independence and Combinations
Chemistry Solutions
Below are examples of Chemistry problems that can be solved.
- Unit Conversion
- Atomic Structure
- Molecules and Compounds
- Chemical Equations and Reactions
- Behavior of Gases
- Solutions and Concentrations
Physics Solutions
Below are examples of Physics math problems that can be solved.
- Static Equilibrium
- Dynamic Equilibrium
- Kinematics Equations
- Electricity
- Thermodymanics
Geometry Graphing Solutions
Below are examples of Geometry and graphing math problems that can be solved.
- Step By Step Graphing
- Linear Equations and Functions
- Polar Equations
Looking for the old Mathway Calculator? We've moved it to here .
Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.
Email Address Sign Up

Or search by topic
Number and algebra
- The Number System and Place Value
- Calculations and Numerical Methods
- Fractions, Decimals, Percentages, Ratio and Proportion
- Properties of Numbers
- Patterns, Sequences and Structure
- Algebraic expressions, equations and formulae
- Coordinates, Functions and Graphs
Geometry and measure
- Angles, Polygons, and Geometrical Proof
- 3D Geometry, Shape and Space
- Measuring and calculating with units
- Transformations and constructions
- Pythagoras and Trigonometry
- Vectors and Matrices
Probability and statistics
- Handling, Processing and Representing Data
- Probability
Working mathematically
- Thinking mathematically
- Mathematical mindsets
- Cross-curricular contexts
- Physical and digital manipulatives
For younger learners
- Early Years Foundation Stage
Advanced mathematics
- Decision Mathematics and Combinatorics
- Advanced Probability and Statistics
Problem Solving
Problem Solving and the New Curriculum Age 5 to 11
Developing a Classroom Culture That Supports a Problem-solving Approach to Mathematics Age 5 to 11
Developing Excellence in Problem Solving with Young Learners Age 5 to 11
Using NRICH Tasks to Develop Key Problem-solving Skills Age 5 to 11
Trial and Improvement at KS1 Age 5 to 7
Trial and Improvement at KS2 Age 7 to 11
Working Systematically - Primary Teachers Age 5 to 11
Number Patterns Age 5 to 11
Working Backwards at KS1 Age 5 to 7
Working Backwards at KS2 Age 7 to 11
Reasoning Age 5 to 11
Visualising at KS1 - Primary Teachers Age 5 to 7
Visualising at KS2 - Primary Teachers Age 7 to 11
Conjecturing and Generalising at KS1 - Primary Teachers Age 5 to 7

Conjecturing and Generalising at KS2 - Primary Teachers Age 7 to 11
- Mathematical Problem Solving in the Early Years
- Low Threshold High Ceiling - an Introduction
- What's All the Talking About?
- Group-worthy Tasks and Their Potential to Support Children to Develop Independent Problem-solving Skills
- Developing the Classroom Culture: Using the Dotty Six Activity as a Springboard for Investigation
Over 5 Billion Problems Solved
Step-by-step examples.
- Adding Using Long Addition
- Long Subtraction
- Long Multiplication
- Long Division
- Dividing Using Partial Quotients Division
- Converting Regular to Scientific Notation
- Arranging a List in Order
- Expanded Notation
- Prime or Composite
- Comparing Expressions
- Converting to a Percentage
- Finding the Additive Inverse
- Finding the Multiplicative Inverse
- Reducing Fractions
- Finding the Reciprocal
- Converting to a Decimal
- Converting to a Mixed Number
- Adding Fractions
- Subtracting Fractions
- Multiplying Fractions
- Dividing Fractions
- Converting Ratios to Fractions
- Converting Percents to Decimal
- Converting Percents to Fractions
- Converting the Percent Grade to Degree
- Converting the Degree to Percent Grade
- Finding the Area of a Rectangle
- Finding the Perimeter of a Rectangle
- Finding the Area of a Square
- Finding the Perimeter of a Square
- Finding the Area of a Circle
- Finding the Circumference of a Circle
- Finding the Area of a Triangle
- Finding the Area of a Trapezoid
- Finding the Volume of a Box
- Finding the Volume of a Cylinder
- Finding the Volume of a Cone
- Finding the Volume of a Pyramid
- Finding the Volume of a Sphere
- Finding the Surface Area of a Box
- Finding the Surface Area of a Cylinder
- Finding the Surface Area of a Cone
- Finding the Surface Area of a Pyramid
- Converting to a Fraction
- Simple Exponents
- Prime Factorizations
- Finding the Factors
- Simplifying Fractions
- Converting Grams to Kilograms
- Converting Grams to Pounds
- Converting Grams to Ounces
- Converting Feet to Inches
- Converting to Meters
- Converting Feet to Miles
- Converting Feet to Yards
- Converting to Feet
- Converting to Yards
- Converting Miles to Feet
- Converting Miles to Kilometers
- Converting Miles to Yards
- Converting Kilometers to Miles
- Converting Kilometers to Meters
- Converting Meters to Feet
- Converting Meters to Inches
- Converting Ounces to Grams
- Converting Ounces to Pounds
- Converting Ounces to Tons
- Converting Pounds to Grams
- Converting Pounds to Ounces
- Converting Pounds to Tons
- Converting Yards to Feet
- Converting Yards to Millimeters
- Converting Yards to Inches
- Converting Yards to Miles
- Converting Yards to Meters
- Converting Fahrenheit to Celsius
- Converting Celsius to Fahrenheit
- Finding the Median
- Finding the Mean (Arithmetic)
- Finding the Mode
- Finding the Minimum
- Finding the Maximum
- Finding the Lower or First Quartile
- Finding the Upper or Third Quartile
- Finding the Five Number Summary
- Finding a Point's Quadrant
- Finding the Midpoint of a Line Segment
- Distance Formula
- Arithmetic Operations
- Combining Like Terms
- Determining if the Expression is a Polynomial
- Distributive Property
- Simplifying
- Multiplication
- Polynomial Addition
- Polynomial Subtraction
- Polynomial Multiplication
- Polynomial Division
- Simplifying Expressions
- Evaluate the Expression Using the Given Values
- Multiplying Polynomials Using FOIL
- Identifying Degree
- Operations on Polynomials
- Negative Exponents
- Evaluating Radicals
- Solving by Adding/Subtracting
- Solving by Multiplying/Dividing
- Solving Containing Decimals
- Solving for a Variable
- Solving Linear Equations
- Solving Linear Inequalities
- Finding the Quadratic Constant of Variation
- Converting the Percent Grade to Slope
- Converting the Slope to Percent Grade
- Finding Equations Using Slope-Intercept
- Finding the Slope
- Finding the y Intercept
- Calculating Slope and y-Intercept
- Rewriting in Slope-Intercept Form
- Finding Equations Using the Slope-Intercept Formula
- Finding Equations Using Two Points
- Finding a Perpendicular Line Containing a Given Point
- Finding a Parallel Line Containing a Given Point
- Finding a Parallel Line to the Given Line
- Finding a Perpendicular Line to the Given Line
- Finding Ordered Pair Solutions
- Using a Table of Values to Graph an Equation
- Finding the Equation Using Point-Slope Form
- Finding the Surface Area of a Sphere
- Solving by Graphing
- Finding the LCM of a List of Expressions
- Finding the LCD of a List of Expressions
- Determining if the Number is a Perfect Square
- Finding the Domain
- Evaluating the Difference Quotient
- Solving Using the Square Root Property
- Determining if True
- Finding the Holes in a Graph
- Finding the Common Factors
- Expand a Trinomial with the Trinomial Theorem
- Finding the Start Point Given the Mid and End Points
- Finding the End Point Given the Start and Mid Points
- Finding the Slope and y-Intercept
- Finding the Equation of the Parabola
- Finding the Average Rate of Change
- Finding the Slope of the Perpendicular Line to the Line Through the Two Points
- Rewriting Using Negative Exponents
- Synthetic Division
- Maximum Number of Real Roots/Zeros
- Finding All Possible Roots/Zeros (RRT)
- Finding All Roots with Rational Root Test (RRT)
- Finding the Remainder
- Finding the Remainder Using Long Polynomial Division
- Reordering the Polynomial in Ascending Order
- Reordering the Polynomial in Descending Order
- Finding the Leading Term
- Finding the Leading Coefficient
- Finding the Degree, Leading Term, and Leading Coefficient
- Finding the GCF of a Polynomial
- Factoring Out Greatest Common Factor (GCF)
- Identifying the Common Factors
- Cancelling the Common Factors
- Finding the LCM using GCF
- Finding the GCF
- Factoring Trinomials
- Trinomial Squares
- Factoring Using Any Method
- Factoring a Difference of Squares
- Factoring a Sum of Cubes
- Factoring by Grouping
- Factoring a Difference of Cubes
- Determine if an Expression is a Factor
- Determining if Factor Using Synthetic Division
- Find the Factors Using the Factor Theorem
- Determining if Polynomial is Prime
- Determining if the Polynomial is a Perfect Square
- Expand using the Binomial Theorem
- Factoring over the Complex Numbers
- Finding All Integers k Such That the Trinomial Can Be Factored
- Determining if Linear
- Rewriting in Standard Form
- Finding x and y Intercepts
- Finding Equations Using the Point Slope Formula
- Finding Equations Given Point and y-Intercept
- Finding the Constant Using Slope
- Finding the Slope of a Parallel Line
- Finding the Slope of a Perpendicular Line
- Simplifying Absolute Value Expressions
- Solving with Absolute Values
- Finding the Vertex for the Absolute Value
- Rewriting the Absolute Value as Piecewise
- Calculating the Square Root
- Simplifying Radical Expressions
- Rationalizing Radical Expressions
- Solving Radical Equations
- Rewriting with Rational (Fractional) Exponents
- Finding the Square Root End Point
- Operations on Rational Expressions
- Determining if the Point is a Solution
- Solving over the Interval
- Finding the Range
- Finding the Domain and Range
- Solving Rational Equations
- Adding Rational Expressions
- Subtracting Rational Expressions
- Multiplying Rational Expressions
- Finding the Equation Given the Roots
- Finding the Asymptotes
- Finding the Constant of Variation
- Finding the Equation of Variation
- Substitution Method
- Addition/Elimination Method
- Graphing Method
- Determining Parallel Lines
- Determining Perpendicular Lines
- Dependent, Independent, and Inconsistent Systems
- Finding the Intersection (and)
- Using the Simplex Method for Constraint Maximization
- Using the Simplex Method for Constraint Minimization
- Finding the Union (or)
- Finding the Equation with Real Coefficients
- Solving in Terms of the Arbitrary Variable
- Finding a Direct Variation Equation
- Finding the Slope for Every Equation
- Finding a Variable Using the Constant of Variation
- Quadratic Formula
- Solving by Factoring
- Solve by Completing the Square
- Finding the Perfect Square Trinomial
- Finding the Quadratic Equation Given the Solution Set
- Finding a,b, and c in the Standard Form
- Finding the Discriminant
- Finding the Zeros by Completing the Square
- Quadratic Inequalities
- Rational Inequalities
- Converting from Interval to Inequality
- Converting to Interval Notation
- Rewriting as a Single Interval
- Determining if the Relation is a Function
- Finding the Domain and Range of the Relation
- Finding the Inverse of the Relation
- Finding the Inverse
- Determining if One Relation is the Inverse of Another
- Determining if Surjective (Onto)
- Determining if Bijective (One-to-One)
- Determining if Injective (One to One)
- Rewriting as an Equation
- Rewriting as y=mx+b
- Solving Function Systems
- Find the Behavior (Leading Coefficient Test)
- Determining Odd and Even Functions
- Describing the Transformation
- Finding the Symmetry
- Arithmetic of Functions
- Domain of Composite Functions
- Finding Roots Using the Factor Theorem
- Determine if Injective (One to One)
- Determine if Surjective (Onto)
- Finding the Vertex
- Finding the Sum
- Finding the Difference
- Finding the Product
- Finding the Quotient
- Finding the Domain of the Sum of the Functions
- Finding the Domain of the Difference of the Functions
- Finding the Domain of the Product of the Functions
- Finding the Domain of the Quotient of the Functions
- Finding Roots (Zeros)
- Identifying Zeros and Their Multiplicities
- Finding the Bounds of the Zeros
- Proving a Root is on the Interval
- Finding Maximum Number of Real Roots
- Function Composition
- Rewriting as a Function
- Determining if a Function is Rational
- Determining if a Function is Proper or Improper
- Maximum/Minimum of Quadratic Functions
- Finding All Complex Number Solutions
- Rationalizing with Complex Conjugates
- Vector Arithmetic
- Finding the Complex Conjugate
- Finding the Magnitude of a Complex Number
- Simplifying Logarithmic Expressions
- Expanding Logarithmic Expressions
- Evaluating Logarithms
- Rewriting in Exponential Form
- Converting to Logarithmic Form
- Exponential Expressions
- Exponential Equations
- Converting to Radical Form
- Find the Nth Root of the Given Value
- Simplifying Matrices
- Finding the Variables
- Solving the System of Equations Using an Inverse Matrix
- Finding the Dimensions
- Multiplication by a Scalar
- Subtraction
- Finding the Determinant of the Resulting Matrix
- Finding the Inverse of the Resulting Matrix
- Finding the Identity Matrix
- Finding the Scalar multiplied by the Identity Matrix
- Simplifying the Matrix Operation
- Finding the Determinant of a 2x2 Matrix
- Finding the Determinant of a 3x3 Matrix
- Finding the Determinant of Large Matrices
- Inverse of a 2x2 Matrix
- Inverse of an nxn Matrix
- Finding Reduced Row Echelon Form
- Finding the Transpose
- Finding the Adjoint
- Finding the Cofactor Matrix
- Finding the Pivot Positions and Pivot Columns
- Finding the Basis and Dimension for the Row Space of the Matrix
- Finding the Basis and Dimension for the Column Space of the Matrix
- Finding the LU Decomposition of a Matrix
- Identifying Conic Sections
- Identifying Circles
- Finding a Circle Using the Center and Another Point
- Finding a Circle by the Diameter End Points
- Finding the Parabola Equation Using the Vertex and Another Point
- Finding the Properties of the Parabola
- Finding the Vertex Form of the Parabola
- Finding the Vertex Form of an Ellipse
- Finding the Vertex Form of a Circle
- Finding the Vertex Form of a Hyperbola
- Finding the Standard Form of a Parabola
- Finding the Expanded Form of an Ellipse
- Finding the Expanded Form of a Circle
- Finding the Expanded Form of a Hyperbola
- Vector Addition
- Vector Subtraction
- Vector Multiplication by a Scalar
- Finding the Length
- Finding the Position Vector
- Determining Column Spaces
- Finding an Orthonormal Basis by Gram-Schmidt Method
- Rewrite the System as a Vector Equality
- Finding the Rank
- Finding the Nullity
- Finding the Distance
- Finding the Plane Parallel to a Line Given four 3d Points
- Finding the Intersection of the Line Perpendicular to Plane 1 Through the Origin and Plane 2
- Finding the Eigenvalues
- Finding the Characteristic Equation
- Finding the Eigenvectors/Eigenspace of a Matrix
- Proving a Transformation is Linear
- Finding the Kernel of a Transformation
- Projecting Using a Transformation
- Finding the Pre-Image
- Finding the Intersection of Sets
- Finding the Union of Number Sets
- Determining if a Set is a Subset of Another Set
- Determining if Two Sets are Mutually Exclusive
- Finding the Set Complement of Two Sets
- Finding the Power Set
- Finding the Cardinality
- Finding the Cartesian Product of Two Sets
- Determining if a Set is a Proper Subset of Another Set
- Finding the Function Rule
- Finding the Square or Rectangle Area Given Four Points
- Finding the Square or Rectangle Perimeter Given Four Points
- Finding the Square or Rectangle Area Given Three Points
- Finding the Square or Rectangle Perimeter Given Three Points
- Finding the Equation of a Circle
- Finding the Equation of a Hyperbola
- Finding the Equation of an Ellipse
- Partial Fraction Decomposition
- Finding an Angle Using another Angle
- Pythagorean Theorem
- Finding the Sine
- Finding the Cosine
- Finding the Tangent
- Finding the Trig Value
- Converting to Degrees, Minutes, and Seconds
- Finding Trig Functions Using Identities
- Finding Trig Functions Using the Right Triangle
- Converting Radians to Degrees
- Converting Degrees to Radians
- Finding a Reference Angle
- Finding a Supplement
- Finding a Complement
- Converting RPM to Radians per Second
- Finding the Quadrant of the Angle
- Graphing Sine & Cosine Functions
- Graphing Other Trigonometric Functions
- Amplitude, Period, and Phase Shift
- Finding the Other Trig Values in a Quadrant
- Finding the Exact Value
- Finding the Value Using the Unit Circle
- Expanding Trigonometric Expressions
- Expanding Using Double-Angle Formulas
- Expanding Using Triple-Angle Formulas
- Expanding Using Sum/Difference Formulas
- Simplify Using Pythagorean Identities
- Simplify by Converting to Sine/Cosine
- Inverting Trigonometric Expressions
- Finding the Trig Value of an Angle
- Expanding Using De Moivre's Theorem
- Verifying Trigonometric Identities
- Using Fundamental Identities
- Solving Standard Angle Equations
- Complex Trigonometric Equations
- Solving the Triangle
- Find the Roots of a Complex Number
- Complex Operations
- Trigonometric Form of a Complex Number
- Converting to Polar Coordinates
- Identifying and Graphing Circles
- Identifying and Graphing Limacons
- Identifying and Graphing Roses
- Identifying and Graphing Cardioids
- Difference Quotient
- Finding Upper and Lower Bounds
- Evaluating Functions
- Right Triangle Trigonometry
- Arithmetic Sequences/Progressions
- Geometric Sequences/Progressions
- Finding the Next Term of the Sequence
- Finding the nth Term Given a List of Numbers
- Finding the nth Term
- Finding the Sum of First n Terms
- Expanding Series Notation
- Finding the Sum of the Series
- Finding the Sum of the Infinite Geometric Series
- Converting to Rectangular Coordinates
- Evaluating Limits Approaching a Value
- Evaluating Limits Approaching Infinity
- Finding the Angle Between the Vectors
- Determining if the Point is on the Graph
- Finding the Antiderivative
- Checking if Continuous Over an Interval
- Determining if a Series is Divergent
- Using the Integral Test for Convergence
- Determining if an Infinite Series is Convergent Using Cauchy's Root Test
- Using the Limit Definition to Find the Tangent Line at a Given Point
- Finding the nth Derivative
- Finding the Derivative Using Product Rule
- Finding the Derivative Using Quotient Rule
- Finding the Derivative Using Chain Rule
- Use Logarithmic Differentiation to Find the Derivative
- Finding the Derivative
- Implicit Differentiation
- Using the Limit Definition to Find the Derivative
- Evaluating the Derivative
- Finding Where dy/dx is Equal to Zero
- Finding the Linearization
- Finding a Tangent Line to a Curve
- Checking if Differentiable Over an Interval
- The Mean Value Theorem
- Finding the Inflection Points
- Find Where the Function Increases/Decreases
- Finding the Critical Points of a Function
- Find Horizontal Tangent Line
- Evaluating Limits with L'Hospital Rule
- Local Maxima and Minima
- Finding the Absolute Maximum and Minimum on the Given Interval
- Finding Concavity using the Second Derivative
- Finding the Derivative using the Fundamental Theorem of Calculus
- Find the Turning Points
- Finding the Integral
- Evaluating Definite Integrals
- Evaluating Indefinite Integrals
- Substitution Rule
- Finding the Arc Length
- Finding the Average Value of the Derivative
- Finding the Average Value of the Equation
- Finding Area Between Curves
- Finding the Volume
- Finding the Average Value of the Function
- Finding the Root Mean Square
- Integration by Parts
- Trigonometric Integrals
- Trigonometric Substitution
- Integration by Partial Fractions
- Eliminating the Parameter from the Function
- Verify the Solution of a Differential Equation
- Solve for a Constant Given an Initial Condition
- Find an Exact Solution to the Differential Equation
- Verify the Existence and Uniqueness of Solutions for the Differential Equation
- Solve for a Constant in a Given Solution
- Solve the Bernoulli Differential Equation
- Solve the Linear Differential Equation
- Solve the Homogeneous Differential Equation
- Solve the Exact Differential Equation
- Approximate a Differential Equation Using Euler's Method
- Finding Elasticity of Demand
- Finding the Consumer Surplus
- Finding the Producer Surplus
- Finding the Gini Index
- Finding the Geometric Mean
- Finding the Quadratic Mean (RMS)
- Find the Mean Absolute Deviation
- Finding the Mid-Range (Mid-Extreme)
- Finding the Interquartile Range (H-Spread)
- Finding the Midhinge
- Finding the Standard Deviation
- Finding the Skew of a Data Set
- Finding the Range of a Data Set
- Finding the Variance of a Data Set
- Finding the Class Width
- Solving Combinations
- Solving Permutations
- Finding the Probability of Both Independent Events
- Finding the Probability of Both Dependent Events
- Finding the Probability for Both Mutually Exclusive Events
- Finding the Conditional Probability for Independent Events
- Determining if Given Events are Independent/Dependent Events
- Determining if Given Events are Mutually Exclusive Events
- Finding the Probability of Both not Mutually Exclusive Events
- Finding the Conditional Probability Using Bayes' Theorem
- Finding the Probability of the Complement
- Describing Distribution's Two Properties
- Finding the Expectation
- Finding the Variance
- Finding the Probability of a Binomial Distribution
- Finding the Probability of the Binomial Event
- Finding the Mean
- Finding the Relative Frequency
- Finding the Percentage Frequency
- Finding the Upper and Lower Class Limits of the Frequency Table
- Finding the Class Boundaries of the Frequency Table
- Finding the Class Width of the Frequency Table
- Finding the Midpoints of the Frequency Table
- Finding the Mean of the Frequency Table
- Finding the Variance of the Frequency Table
- Finding the Standard Deviation of the Frequency Table
- Finding the Cumulative Frequency of the Frequency Table
- Finding the Relative Frequency of the Frequency Table
- Finding the Median Class Interval of the Frequency Table
- Finding the Modal Class of the Frequency Table
- Creating a Grouped Frequency Distribution Table
- Finding the Data Range
- Finding a z-Score for a Normal Distribution
- Approximating Using Normal Distribution
- Finding the Probability of the z-Score Range
- Finding the Probability of a Range in a Nonstandard Normal Distribution
- Finding the z-Score Using the Table
- Finding the z-Score
- Testing the Claim
- Finding a t-Value for a Confidence Level
- Finding the Critical t-Value
- Setting the Alternative Hypothesis
- Setting the Null Hypothesis
- Determining if Left, Right, or Two Tailed Test Given the Null Hypothesis
- Determining if Left, Right, or Two Tailed Test Given the Alternative Hypothesis
- Finding Standard Error
- Finding the Linear Correlation Coefficient
- Determining if the Correlation is Significant
- Finding a Regression Line
- Cramer's Rule
- Solving using Matrices by Elimination
- Solving using Matrices by Row Operations
- Solving using an Augmented Matrix
- Finding the Simple Interest Received
- Finding the Present Value with Compound Interest
- Finding the Simple Interest Future Value
- Finding the Future Value with Continuous Interest
- Finding the Norm in Real Vector Space
- Finding the Direction Angle of the Vector
- Finding the Cross Product of Vectors
- Finding the Dot Product of Vectors
- Determining if Vectors are Orthogonal
- Finding the Distance Between the Vectors
- Finding a Unit Vector in the Same Direction as the Given Vector
- Finding the Angle Between Two Vectors Using the Cross Product
- Finding the Angle Between Two Vectors Using the Dot Product
- Finding the Projection of One Vector Onto another Vector
- Matrices Addition
- Matrices Subtraction
- Matrices Multiplication
- Finding the Trace
- Finding the Basis
- Matrix Dimension
- Convert to a Linear System
- Diagonalizing a Matrix
- Determining the value of k for which the system has no solutions
- Linear Independence of Real Vector Spaces
- Finding the Null Space
- Determining if the Vector is in the Span of the Set
- Finding the Number of Protons
- Finding the Number of Electrons
- Finding the Number of Neutrons
- Finding the Mass of a Single Atom
- Finding the Electron Configuration
- Finding the Atomic Mass
- Finding the Atomic Number
- Finding the Mass Percentages
- Finding Oxidation Numbers
- Balancing Chemical Equations
- Balancing Burning Reactions
- Finding the Density at STP
- Determining if the Compound is Soluble in Water
- Finding Mass
- Finding Density
- Finding Weight
- Finding Force
- Finding the Work Done
- Finding Angular Velocity
- Finding Centripetal Acceleration
- Finding Final Velocity
- Finding Average Acceleration
- Finding Displacement
- Finding Voltage Using the Ohm's Law
- Finding Electrical Power
- Finding Kinetic Energy
- Finding Power
- Finding Wavelength
- Finding Frequency
- Finding Pressure of the Gas
Popular Problems
- Pre-Algebra
- Trigonometry
- Precalculus
- Finite Math
- Linear Algebra
- Recent Popular Problems
Calculator Pages
Formula pages.
- Algebra Formulas
- Trigonometry Formulas
- Geometric Formulas
- Terms ( Premium )
- DO NOT SELL MY INFO
- Mathway © 2024
Please ensure that your password is at least 8 characters and contains each of the following:
- a special character: @$#!%*?&

Compute expert-level answers using Wolfram’s breakthrough algorithms, knowledgebase and AI technology  Mathematics ›
Science & Technology ›
Society & Culture ›
Everyday Life ›
 Upload a screenshot and solve any math, physics, or accounting problem instantly with MathGPT!Drag & drop an image file here, or click to select an image. Drag image here or click to upload The Must-Have Math AI & Calculator for StudentsDon't stress over math for another minute. Instantly get step-by-step solutions to all types of math problems. Try our math solver for free. Instantly Solve Math Problems with Our Math AI ToolStop searching for math answers in the back of the textbook. Mathful's math solver shows you how to get there yourself. Type or upload a photo of any math question, and we will provide the full working out, so you can learn as you go.  Cutting-Edge Photo Math Solver that Outshines ChatGPTOur photo math solver can instantly scan image uploads of math problems to provide step-by-step solutions with unmatched accuracy and precision, making it a far more powerful alternative to conversational AI tools like ChatGPT. Key Features of Our Powerful Math AI Solver 98% AccurateOur AI math solver provides step-by-step math answers with an unparalleled level of precision, ensuring accurate solutions for your math problems.  Forget about expensive math tutors our AI math solver helps you or your children solve math problems for free in one click. Save money while getting accurate solutions.  10+ Math Branches CoveredOur AI math problem solver helps you effortlessly handle questions in various mathematical subjects, including algebra, calculus, geometry, and more.  24/7 SolutionsGet detailed, step-by-step mathematical explanations 24/7 from our AI math problem solver. Master math effortlessly online. Quick & Precise Math Calculator With StepsUsing advanced AI algorithms, our step-by-step math calculator can process complex math problems to generate accurate and detailed solutions in seconds. They include:
 3 Simple Steps to Use Our Math Solver & CalculatorHave trouble with a math problem or just want to check your work? Our math AI is ready to help. Here's how:  Input Your Math ProblemType the math problem into the input box or upload an image of the math problem. Alternatively, input the problem into our math calculator. 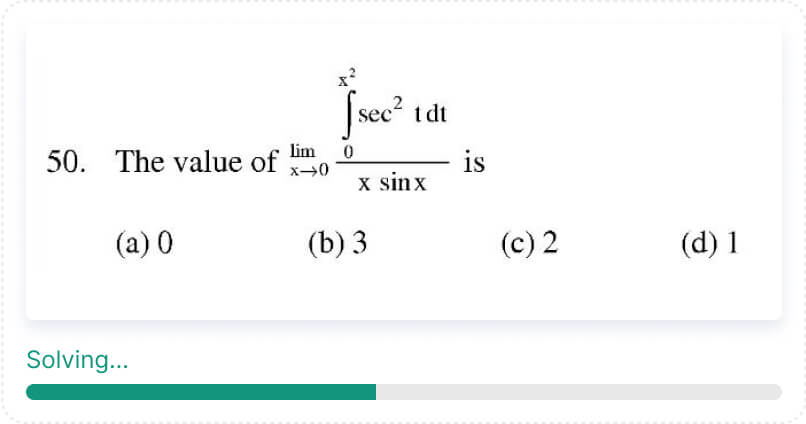 Let Mathful Formulate a SolutionOur math AI or math calculator will work to generate a detailed, accurate solution to your math problem.  Get Math Answer InstantlyNearly instantly you'll receive the step-by-step answer to your math problem so you can actually learn. Can a math AI help me improve my math grades in school?Certainly! A math solver like Mathful can significantly boost your math grade by offering round-the-clock access to step-by-step solutions across a wide array of math topics, from algebra to calculus. Does this math AI tool cover all types of math?Yes, Mathful is capable of tackling any type of math question, from arithmetic and geometry to algebra and number theory. How long does it take for the math AI solver to get an answer to my math question?Once you submit your math problem, Mathful will quickly formulate the correct answer and generate a solution almost instantly. Can I try the Mathful AI math solver for free?Yes, the Mathful AI math problem solver is free to try. Cost-friendly subscriptions are available to ask even more math questions. Is the math solver and math calculator accurate?Yes, the math solver and step-by-step math calculator provided by Mathful are designed to deliver highly accurate results. Utilizing advanced AI algorithms, these tools process and solve a vast range of math problems with precision. Is the math AI and math calculator safe to use?Yes, our math solver and step-by-step math calculator use encrypted transmissions, and your personal information is never stored or shared. It was created with your privacy and safety in mind. Why should I use a photo math solver?By using a photo math solver, you can simply take a photo of a math problem. No more need to type out complex equations or search for similar examples online. It's an instant way to begin tackling your math homework or study questions. What problems can I solve with a math calculator?With a math calculator from Mathful, you can solve a broad spectrum of mathematical problems across various domains, including basic arithmetic operations, algebraic equations, and geometry calculations to more complex calculus derivatives and integrals.  Solve Math Problems Easily with Our Math Solver & Math CalculatorGet instant, accurate answers to your math problems and boost your math grade. Try our AI math problem solver and math calculator with steps for free today. Counting on mathsOne team’s mission to raise humanity’s next-generation problem solvers By Tom Almeroth-Williams  Image: skynesher The world needs more people who can think mathematically to solve its mounting problems.This is what drives the researchers behind nrich , cambridge’s flagship maths outreach project.. Now celebrating its 25 th anniversary, NRICH spent the last two years in unexpected emergency rescue mode, helping learners in Covid-19 lockdown. The team continues to support the post-pandemic catch-up effort but Director Dr Ems Lord also has her sights set on big plans for the future. “Our online resources were getting over a million page views per week,” Lord recalls. “ We were ready from day one of lockdown, and the huge response showed just how much that was needed.” In Spring 2020, the UK Government highlighted NRICH resources to schools and the team contributed to the BBC’s heavily used Bitesize maths resources. Between March and September 2020, nrich.maths.org registered a 95% increase in UK visits compared to the previous year. In the 2020–21 school year alone, the site attracted just under 33 million page views. “We were about to publish new resources for schools which had been a huge amount of work,” Lord recalls. “We just dropped that and started gathering all the resources we knew families could do at home with buttons, counters, beans, whatever they had lying around, plus all the interactive games we had.” Maths at Home catered, and still does, for every key stage from early years to sixth form and went live the very day that England sent its schoolchildren home. The following Monday, visits to the NRICH website immediately surged. Professor Colm-Cille Caulfield, head of Cambridge’s department of applied maths and theoretical physics, says: “The NRICH team had all the right skills, ideas and resources to respond to the pandemic. They pivoted amazingly to home learning and sorted out a huge amount of support for people across the globe. It was amazing to watch them do it.” Dr Ems Lord, Director of NRICH. Image: Nathan Pitt NRICH at 25 film:The complete package, nrich, so-called because it seeks to enrich the teaching and learning of mathematics, has designed thousands of online resources for every stage of early years, primary and secondary school education.. Based at Cambridge’s Faculty of Mathematics, the project has always shared its materials online, free of charge and without any barriers, internationally. Its current team of seven includes a researcher, experienced teachers and web developers. NRICH focuses on building problem-solving skills, perseverance, mathematical reasoning, ability to apply knowledge creatively in unfamiliar contexts, and confidence in tackling new challenges. The team designs what it calls 'low threshold high ceiling' resources to be accessible to all learners, encourage exploration and discussion. NRICH has always had a penchant for fun titles and real-world set-ups, as in Dodgy proofs ; Olympic Torch Tour , Wipeout ; Egyptian rope ; National flags ; and Scratch cards . In addition to its brimming reservoir of resources, the team posts live problems so students can share their solutions for publication on the site. Recently, the team posted solutions to an odd numbers problem from a student at Buckler's Mead Academy in Somerset, a British School in Oman, and the London Academy in Morocco. Teachers also regularly Tweet about using NRICH in the classroom. Well done, Y2s! We're delighted that you enjoyed exploring this challenge, thanks for sharing your photos with our team. PS If other classes would like to explore Chain of Changes too, here's the task, teacher notes and more examples of classroom work https://t.co/bZirUPGhJb https://t.co/gDhfxagrlL — NRICH maths (@nrichmaths) March 9, 2022 Students are encouraged to visit the website themselves at home, not least during lockdowns, but NRICH has always seen working with teachers as the most effective and efficient way to serve as many young people as possible. For this reason, the team provides specialist in-person and webinar training, plus resource-specific notes, for teachers to help them build lessons around ready-to-go tasks and maximise their impact in the classroom. The team also organises webinars for thousands of students from across the world.  Poster for a problem aimed at 11 – 16 year olds Education, education, educationRemember that speech well, back in 1996, around the time tony blair was declaring these priorities for government, researchers at cambridge’s education faculty were brainstorming what would become nrich.. Ems Lord explains: “There's a long history of people sharing maths problems and solutions with each other, but that used to be slow and small-scale. When the internet arrived, colleagues at Education decided to create an online maths club.” “Meanwhile, researchers here at Maths were thinking about how to mark the new millennium with a public outreach project. It made sense to bring both together so today NRICH is at the heart of The Millennium Mathematics Project .” NRICH remains a collaboration between the two faculties. Lord took charge in 2015, following a career as a maths teacher, local authority consultant and head of one of the country's largest maths teacher training professional development programmes. She was president of the Mathematical Association in 2019–20 and is a regular contributor to the All-Party Parliamentary Group for the Teaching Profession, as well as being a member of the Joint Mathematical Council and a founding fellow of the Chartered College of Teachers. Complementing her work at NRICH, Lord uses her research fellowship at Clare Hall to identify ways to improve student outcomes, address the gender imbalance in mathematics study post-16 and widen participation in the subject. Lord says: “As many children get older, their curiosity often dips. And in this country especially, there are pervasive negative attitudes towards maths, so it's important that we catch people young and sustain their interest.” “It's impossible to separate mathematics from imagination.”Dr Ems Lord “How do you have a breakthrough if somebody isn't curious and thinking, ‘I wonder if that's where the magic happens?’ Imagination is how we go from just solving problems to posing even more ambitious questions and moving forwards. “What's really special about NRICH is that we encourage children to problem solve in different ways, take different approaches, and use and apply their maths. And by doing that, when students leave school, they are truly ready to solve problems.” To take just one example, in Tree tops , a challenge aimed at 14–16 year olds, NRICH users are invited to enter the forestry business and work out the maximum profit that they could make after 100 years. Curriculum cubedIn 1996, tony blair complained that the uk was, “35th in the world league of education standards … they say give me the boy at seven, i’ll show you the man at 70. well give me the education system that is 35th in the world today and i will give you the economy that is 35th in the world tomorrow.”. There have been significant signs of improvement since then, not least in mathematics. In 2019, the Pisa tests, run by the Organisation for Economic Co-operation and Development, ranked the country 18 th for mathematics. “The UK education system has done fantastic things,” says Lord, “but big challenges remain.” She points out that while maths is now the most popular A-Level subject, only 6% of maths professors in the UK are female. “We still have a lot of work to do on that front. We need to ensure that the subject reflects the country’s diversity in lots of other ways too.”  Teamwork at an NRICH resilience workshop. Image: MMP/Nigel Luckhurst NRICH maps onto the national curriculum for mathematics, which currently has three major strands: fluency, reasoning and problem solving. But even Ofsted, the school inspectors, admit that there isn’t enough emphasis on problem solving. If this is going to change, schools, students and policy makers will need to make even greater use of NRICH. “Yes, we can improve exam performance,” says Lord, “ but our ultimate goal is to help students to think flexibly and solve problems.” “In the UK, assessments at primary and secondary schools focus on number skills. These are important, of course. We need to know when our calculations are accurate, but we also need to value problem solving because that's what we face in everyday life. That isn’t evident in our exams yet.” “There’s a difference between passing an exam and thinking like a mathematician. NRICH focuses on the latter.”Ems Lord, Director of NRICH At the same time, Lord thinks that the UK curriculum needs to put greater emphasis on developing collaborative skills, something which she has discussed with the All-Party Parliamentary Group for the Teaching Profession. Lord remembers a six-year-old telling her that she couldn’t work on a maths task with someone else because it would be cheating. “I was horrified,” she says. "Solving problems together is crucial. If you want proof of that just walk around our faculty and you’ll find some of the greatest mathematicians in the world working in teams all the time.” Teacher’s reportMark dawes , an experienced maths teacher at comberton village college in cambridgeshire has been using nrich ever since it was launched.. “A problem is, by definition, difficult,” he says, “so having high-quality problems that are really interesting, that create opportunities to try things out, and encourage pupils to share their ideas, that’s extremely powerful. As teachers, we just don't have time to sit down every week to devise new problems of this quality. “Even when I’ve already solved the problems myself, when I teach with an NRICH resource, my pupils almost always come up with something that I hadn't thought of, and that democratises the classroom.” “There are jobs that require a very deep mathematical understanding, but not everyone is going to become a computer programmer. What we do all need, however, is to be able to critically analyse what’s going on around us, to make decisions based on data and reasoning. “NRICH helps pupils to use the full range of their maths skills and opportunities to apply them. And it shows them how useful maths can be in so many different ways.”Image captions.  Going forwards, Ems Lord hopes to work even more closely with government to ensure that future generations have the problem solving skills that they will need.She says: “Whether you’re fighting the spread of infectious diseases, trying to prevent climate change or adapt to increasing automation at work, you need people with curious minds who can work flexibly, make connections and collaborate. And that's why NRICH is so important.” Professor Caulfield agrees: “We need to embed mathematics, and an understanding of how it plays a role in absolutely everything, in our education system. “NRICH teaches people to think like mathematicians and learn how to solve problems, the kind of problem-solving that will allow us to have a sustainable and healthy society.”Professor Colm-Cille Caulfield “As the internet and all of its data become more important in our lives, we have to adapt to cope with that. “Understanding how mathematics underpins data and how you use it to solve problems is exactly what NRICH communicates to every child.” Julia Gog, Professor of mathematical biology at Cambridge and another long-term NRICH supporter, says: “The pandemic has shown that mathematical literacy for everyone is more important than ever. “The more you have, the more you can make sense of what is happening around you, ask the right questions and make informed personal choices.” Ems Lord sees an exciting future for NRICH. In the medium term, the team will be working to make it even easier for teachers to deliver sequences of lessons which develop and embed key transferable skills among their students. Longer term, they hope to harness advances in AI, and adapt work already being done in the Maths Faculty on medical imaging, to make NRICH more responsive to how individual students think. Lord says: “When a student gets stuck, we want to our resources to be capable of prompting them with personalised next steps, offering different visuals and approaches. This will take time, but we need to aim high and tap in to the research happening around us.”  ...visit our interactive map to find out how. Find out how you can support NRICH here .  Professor Julia Gog Explore nrich.maths.org Published 30 March 2022 With thanks to: All of the outstanding people who have made NRICH such a success over the past 25 years Mark Dawes and Comberton Village College Professors Colm-Cille Caulfield and Julia Gog Words: Tom Almeroth-Williams Film by Jonathan Settle. Story designed with Alison Fair The text in this work is licensed under a Creative Commons Attribution 4.0 International License  7 of the hardest problems in mathematics that have been solvedMathematics is full of problems, some of which have been solved and others that haven’t. here, we focus on 7 of the hardest problems that have been solved.. Tejasri Gururaj  What are the hardest problems in math that have already been solved? intararit
Some mathematical problems are challenging even for the most accomplished mathematicians. From the Poincaré conjecture to Fermat’s last theorem , here we take a look at some of the most challenging math problems ever solved. 1. Poincaré conjecture Salix alba The Poincaré conjecture is a famous problem in topology, initially proposed by French mathematician and theoretical physicist Henri Poincaré in 1904. It asserts that every simply connected, closed 3-manifold is topologically homeomorphic (a function that is a one-to-one mapping between sets such that both the function and its inverse are continuous) to a 3-dimensional sphere. In simpler terms, the conjecture asserts that a particular group of three-dimensional shapes can be continuously transformed into a sphere without any gaps or holes. The problem was solved by the reclusive Russian mathematician Grigori Perelman in 2003. He built upon the work of American mathematician Richard S. Hamilton’s program involving the Ricci flow. What makes this achievement even more remarkable is that Perelman declined the prestigious Fields Medal and the Clay Millennium Prize reward that came with it. He chose to stay away from the spotlight and mathematical acclaim, but his proof withstood rigorous scrutiny from the mathematical community. The resolution of the Poincaré conjecture confirmed the fundamental role of topology in understanding the shape and structure of spaces, impacting fields like geometry and manifold theory. 2. The prime number theorem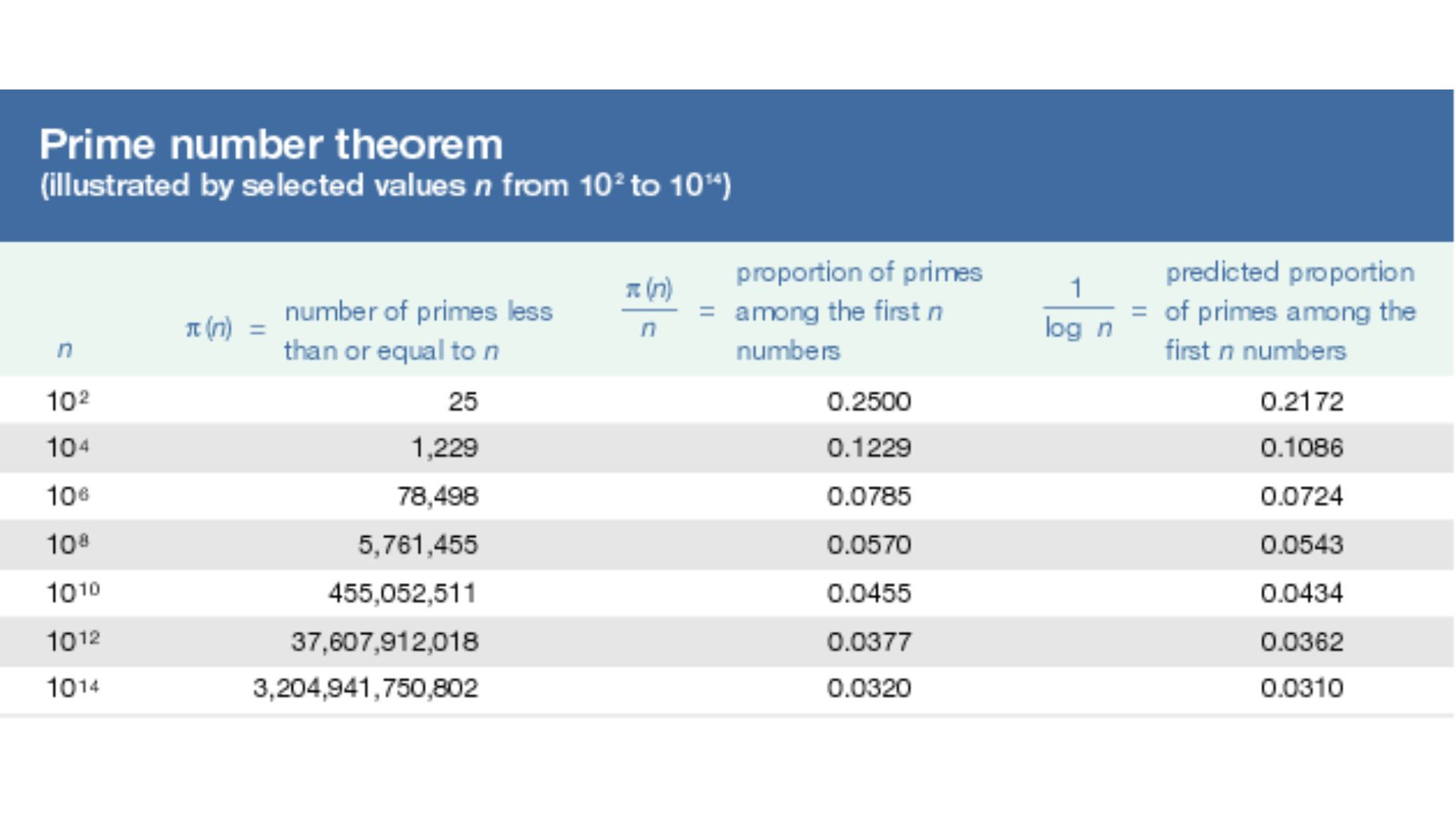 Britannica The prime number theorem long stood as one of the fundamental questions in number theory. At its core, this problem is concerned with unraveling the distribution of prime numbers. The question at hand revolves around the distribution pattern of these primes within the realm of natural numbers. Are there any discernible patterns governing the distribution of prime numbers, or do they appear to be entirely random? The theorem states that for large values of x, π(x) is approximately equal to x/ln(x). The breakthrough in solving this theorem came in the late 19th century, thanks to the independent work of two mathematicians, Jacques Hadamard and Charles de la Vallée-Poussin. In 1896, both mathematicians presented their proofs of the theorem. Their work demonstrated that prime numbers exhibit a remarkable, asymptotic distribution pattern . Their solution produced the insight that, as one considers larger and larger numbers, the density of prime numbers diminishes. The theorem precisely characterized the rate of this decrease, showing that prime numbers become less frequent as we move along the number line. It’s as if they gradually thin out, although they never entirely vanish. The prime number theorem was a turning point in the study of number theory . It provided profound insights into the distribution of prime numbers and put to rest the notion that there might exist a formula predicting each prime number. Instead, it proposed a probabilistic approach to understanding the distribution of prime numbers. The theorem’s significance extends into various mathematical fields, especially in cryptography, where the properties of prime numbers play a pivotal role in securing communications. 3. Fermat’s last theorem Charles Rex Arbogast/AP via NPR Fermat’s last theorem is one of the problems on this list many people are most likely to have heard of. The conjecture, proposed by French mathematician Pierre de Fermat in the 17th century, states that it’s impossible to find three positive integers, a, b, and c, that can satisfy the equation a n + b n = c n for any integer value of n greater than 2. For instance, there are no whole number values of a, b, and c that can make 3 3 + 4 3 = 5 3 true. This problem remained unsolved for centuries and became one of the most challenging problems in mathematics. It was made more enticing because Fermat apparently wrote a note in his copy of the Arithmetica by Diophantus of Alexandria, saying, “I have discovered a truly remarkable proof [of this theorem], but this margin is too small to contain it.” Numerous mathematicians attempted to prove or disprove Fermat’s conjecture, but it wasn’t until 1994 that the breakthrough came. The solution was achieved by British mathematician Andrew Wiles, who built upon the work of many other mathematicians who had contributed to the field of number theory. Wiles’ proof was extraordinarily complex and required intricate mathematical concepts and theorems, particularly those related to elliptic curves and modular forms. Wiles’ remarkable proof of Fermat’s last theorem confirmed that the conjecture was indeed true. Having taken more than three centuries to be solved, it had a profound impact on the world of mathematics, demonstrating the power of advanced mathematical techniques in solving long-standing problems.  Z. Ziegler, M. Ondrachek Before Wiles presented its proof, it was in the Guinness Book of World Records as the “most difficult mathematical problem,” in part because the theorem has seen the greatest number of unsuccessful proofs. 4. Classification of finite simple groups Jakob.scholbach/Pbroks13 This one is a bit different from the others on the list. The classification of finite simple groups , also known as the “enormous theorem,” set out to classify all finite simple groups, which are the fundamental building blocks of group theory. Finite simple groups are those groups that cannot be divided into smaller non-trivial normal subgroups. The goal was to understand and categorize all the different types of finite simple groups that exist. The solution to this problem is not straightforward. The proof is a collaborative effort by hundreds of mathematicians covering tens of thousands of pages in hundreds of journal articles published between 1955 and 2004. It is one of the most extensive mathematical proofs ever produced and marks a monumental achievement in group theory. The proof outlines the structure of finite simple groups and demonstrates that they can be classified into several specific categories. This achievement paved the way for a deeper understanding of group theory and its applications in various mathematical fields. 5. The four color theorem Inductiveload The four color theorem tackles an intriguing question related to topology and stands as one of the first significant theorems proved by a computer. It states that any map in a plane can be colored using four colors so that no two adjacent regions share the same color while using the fewest possible colors. Adjacent, in this context, means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet. The theorem doesn’t focus on the artistic aspect of map coloring but rather on the fundamental mathematical principles that underlie it. The solution to this theorem arrived in 1976, thanks to the combined efforts of mathematicians Kenneth Appel and Wolfgang Haken. However, the proof was not widely accepted due to the infeasibility of checking it by hand. Appel and Haken’s achievement confirmed that any map, regardless of its complexity, can be colored with just four colors such that no two neighboring regions share the same color. While the idea seems simple, proving it rigorously was complex and time-consuming. To address any lingering skepticism about the Appel–Haken proof, a more accessible proof using similar principles and still utilizing computer assistance was presented in 1997 by Robertson, Sanders, Seymour, and Thomas. Additionally, in 2005, Georges Gonthier achieved a proof of the theorem using general-purpose theorem-proving software, reinforcing the credibility of the four color theorem. This theorem is not actually used in map-making but has far-reaching implications in various fields, from graph theory to computer science, where it finds applications in scheduling, circuit design, and optimization problems. 6. Gödel’s incompleteness theorems Andrew Das Arulsamy/Research Gate Gödel’s incompleteness theorems , formulated by Austrian mathematician Kurt Gödel in the 20th century, delve into the mysteries of formal systems and their inherent limitations. In mathematics, a formal system has a structured and well-defined framework or language that comprises a set of symbols, rules, and axioms employed for representing and manipulating mathematical or logical expressions. Gödel’s first incompleteness theorem explores a fundamental question: In any consistent formal system, are there true mathematical statements that are undecidable within that system? In other words, do statements exist that cannot be proven as either true or false using the rules and axioms of that system? The second incompleteness theorem takes this further: Can any consistent formal system prove its own consistency? Gödel not only posed these questions but also provided the answers. He established, through rigorous mathematical proofs , that there exist true statements within formal systems that cannot be proven within those very systems. In essence, the first theorem asserts that there are statements that cannot be proven as either true or false using the rules and axioms of a system. The second theorem demonstrates that no consistent formal system can prove its own consistency. Gödel’s theorems introduced a profound paradox within the realm of mathematical logic: There are truths that exist beyond the reach of formal proofs, and there are limits to what can be achieved through mathematical systems alone. Gödel’s contributions to mathematical logic influenced the philosophy of mathematics and our understanding of the inherent limits of formal systems. 7. The goat problem Mnchnstnr The goat problem is a much more recently solved mathematical problem. It involves calculating the grazing area for a tethered goat. Despite its initial simplicity, mathematicians have pondered this problem for over a century. In its basic form, a goat on a rope can graze in a semicircle with an area of A = 1/2πr 2 , where r is the rope’s length. However, the problem becomes more complex when you change the shape of the area the goat can access. For instance, when tethered to a square barn, the goat can access more than just a semicircle. The goat can also go around the corners of the barn, creating additional quarter circles. Mathematician Ingo Ullisch recently unraveled the goat grazing problem, introducing complex analysis into the equation. However, the solution is far from elementary. It involves intricate calculations, relying on the ratio of contour integral expressions and involves numerous trigonometric terms . Although the solution may not offer a practical guide for goat owners, it represents a significant achievement in the world of mathematics. RECOMMENDED ARTICLESWhat makes the goat problem truly fascinating is its capacity to act as a mathematical Rosetta stone , transcending boundaries between various fields and serving as a versatile challenge for experts from diverse disciplines. From age-old conundrums that took centuries to crack to enigmas that continue to elude solutions, mathematical mysteries remind us that the pursuit of knowledge is an ever-evolving journey. So, the next time you find yourself pondering a difficult math problem, remember that you are in good company, following in the footsteps of the greatest mathematical explorers! The Blueprint DailyStay up-to-date on engineering, tech, space, and science news with The Blueprint. By clicking sign up, you confirm that you accept this site's Terms of Use and Privacy Policy ABOUT THE EDITORTejasri Gururaj Tejasri is a versatile Science Writer & Communicator, leveraging her expertise from an MS in Physics to make science accessible to all. In her spare time, she enjoys spending quality time with her cats, indulging in TV shows, and rejuvenating through naps. POPULAR ARTICLESChina plans dual spacecraft to attack, observe 100-foot-wide space rock. 14 hours ago Elon Musk denies ‘volunteering’ sperm for Mars colonization, rubbishes reports17 hours ago Dune come true: Sci-fi-like spacesuit turns urine into drinking water19 hours ago NASA calculates just how much faster time flies on the moonRelated articles.  China’s deep-sea tank dives record 13,460 feet, mines 441 pounds of minerals Scientists beat supercomputers with quantum tech that simulates electron motion Record 56 Chinese warplanes breach Taiwan airspace in a day amid US Pacific drills The MANPADS strike back: Stinger and Starstreak uncoveredMathematicians Are Edging Close to Solving One of the World's 7 Hardest Math ProblemsAnd there’s $1 million at stake. 
The “Millennium Problems” are seven infamously intractable math problems laid out in the year 2000 by the prestigious Clay Institute, each with $1 million attached as payment for a solution. They span all areas of math , as the Clay Institute was founded in 1998 to push the entire field forward with financial support for researchers and important breakthroughs. But the only solved Millennium Problem so far, the Poincare conjecture, illustrates one of the funny pitfalls inherent to offering a large cash prize for math. The winner, Grigori Perelman, refused the Clay prize as well as the prestigious Fields Medal. He withdrew from mathematics and public life in 2006, and even in 2010, he still insisted his contribution was the same as the mathematician whose work laid the foundation on which he built his proof, Richard Hamilton. Math, all sciences, and arguably all human inquiries are filled with pairs or groups that circle the same finding at the same time until one officially makes the breakthrough. Think about Sir Isaac Newton and Gottfried Leibniz, whose back-and-forth about calculus led to the combined version of the field we still study today. Rosalind Franklin is now mentioned in the same breath as her fellow discoverers of DNA, James Watson and Francis Crick. Even the Bechdel Test for women in media is sometimes called the Bechdel-Wallace Test, because humans are almost always in collaboration. That’s what makes this new paper so important. Two mathematicians—Larry Guth of the Massachusetts Institute of Technology (MIT) and James Maynard of the University of Oxford—collaborated on the new finding about how certain polynomials are formed and how they reach out into the number line. Maynard is just 37, and won the Fields Medal himself in 2022. Guth, a decade older, has won a number of important prizes with a little less name recognition. The Riemann hypothesis is not directly related to prime numbers , but it has implications that ripple through number theory in different ways (including with prime numbers). Basically, it deals with where and how the graph of a certain function of complex numbers crosses back and forth across axes. The points where the function crosses an axis is called a “zero,” and the frequency with which those zeroes appear is called the zero density. In the far reaches of the number line, prime numbers become less and less predictable (in the proverbial sense). They are not, so far, predictable in the literal sense—a fact that is an underpinning of modern encryption , where data is protected by enormous strings of integers made by multiplying enormous prime numbers together. The idea of a periodic table of primes, of any kind of template that could help mathematicians better understand where and how large primes cluster together or not, is a holy grail. In the new paper, Maynard and Guth focus on a new limitation of Dirichlet polynomials. These are special series of complex numbers that many believe are of the same type as the function involved in the Riemann hypothesis involves. In the paper, they claim they’ve proven that these polynomials have a certain number of large values, or solutions , within a tighter range than before. In other words, if we knew there might be an estimated three Dirichlet values between 50 and 100 before, now we may know that range to be between 60 and 90 instead. The eye exam just switched a blurry plate for a slightly less blurry one, but we still haven’t found the perfect prescription. “If one knows some more structure about the set of large values of a Dirichlet polynomial, then one can hope to have improved bound,” Maynard and Guth conclude. No, this is not a final proof of the Riemann hypothesis. But no one is suggesting it is. In advanced math, narrowing things down is also vital. Indeed, even finding out that a promising idea turns out to be wrong can have a lot of value—as it has a number of times in the related Twin Primes Conjecture that still eludes mathematicians. In a collaboration that has lasted 160 years and counting, mathematicians continue to take each step together and then, hopefully, compare notes.  Caroline Delbert is a writer, avid reader, and contributing editor at Pop Mech. She's also an enthusiast of just about everything. Her favorite topics include nuclear energy, cosmology, math of everyday things, and the philosophy of it all.  Number LineThe Algebra Calculator is a versatile online tool designed to simplify algebraic problem-solving for users of all levels. Here's how to make the most of it:
algebra-calculator
Please add a message. Message received. Thanks for the feedback. July 1, 2024 The Biggest Problem in Mathematics Is Finally a Step Closer to Being SolvedNumber theorists have been trying to prove a conjecture about the distribution of prime numbers for more than 160 years By Manon Bischoff  Weiquan Lin/Getty Images The Riemann hypothesis is the most important open question in number theory—if not all of mathematics. It has occupied experts for more than 160 years. And the problem appeared both in mathematician David Hilbert’s groundbreaking speech from 1900 and among the “Millennium Problems” formulated a century later. The person who solves it will win a million-dollar prize. But the Riemann hypothesis is a tough nut to crack. Despite decades of effort, the interest of many experts and the cash reward, there has been little progress. Now mathematicians Larry Guth of the Massachusetts Institute of Technology and James Maynard of the University of Oxford have posted a sensational new finding on the preprint server arXiv.org. In the paper, “the authors improve a result that seemed insurmountable for more than 50 years,” says number theorist Valentin Blomer of the University of Bonn in Germany. Other experts agree. The work is “a remarkable breakthrough,” mathematician and Fields Medalist Terence Tao wrote on Mastodon , “though still very far from fully resolving this conjecture.” On supporting science journalismIf you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today. The Riemann hypothesis concerns the basic building blocks of natural numbers: prime numbers, values greater than 1 that are only divisible by 1 and themselves. Examples include 2, 3, 5, 7, 11, 13, and so on.* Every other number, such as 15, can be clearly broken down into a product of prime numbers: 15 = 3 x 5. The problem is that the prime numbers do not seem to follow a simple pattern and instead appear randomly among the natural numbers. Nineteenth-century German mathematician Bernhard Riemann proposed a way to deal with this peculiarity that explains how prime numbers are distributed on the number line—at least from a statistical point of view. A Periodic Table for NumbersProving this conjecture would provide mathematicians with nothing less than a kind of “periodic table of numbers.” Just as the basic building blocks of matter (such as quarks, electrons and photons) help us to understand the universe and our world, prime numbers also play an important role, not just in number theory but in almost all areas of mathematics. There are now numerous theorems based on the Riemann conjecture. Proof of this conjecture would prove many other theorems as well—yet another incentive to tackle this stubborn problem. Interest in prime numbers goes back thousands of years. Euclid proved as early as 300 B.C.E. that there are an infinite number of prime numbers. And although interest in prime numbers persisted, it was not until the 18th century that any further significant findings were made about these basic building blocks. As a 15-year-old, physicist Carl Friedrich Gauss realized that the number of prime numbers decreases along the number line. His so-called prime number theorem (not proven until 100 years later) states that approximately n / ln( n ) prime numbers appear in the interval from 0 to n . In other words, the prime number theorem offers mathematicians a way of estimating the typical distribution of primes along a chunk of the number line. The exact number of prime numbers may differ from the estimate given by the theorem, however. For example: According to the prime number theorem, there are approximately 100 / ln(100) ≈ 22 prime numbers in the interval between 1 and 100. But in reality there are 25. There is therefore a deviation of 3. This is where the Riemann hypothesis comes in. This hypothesis gives mathematicians a way to estimate the deviation. More specifically, it states that this deviation cannot become arbitrarily large but instead must scale at most with the square root of n , the length of the interval under consideration. The Riemann hypothesis therefore does not predict exactly where prime numbers are located but posits that their appearance on the number line follows certain rules. According to the Riemann hypothesis, the density of primes decreases according to the prime number theorem, and the primes are evenly distributed according to this density. This means that there are no large areas in which there are no prime numbers at all, while others are full of them. You can also imagine this idea by thinking about the distribution of molecules in the air of a room: the overall density on the floor is somewhat higher than on the ceiling, but the particles—following this density distribution—are nonetheless evenly scattered, and there is no vacuum anywhere. A Strange ConnectionRiemann formulated the conjecture named after him in 1859, in a slim, six-page publication (his only contribution to the field of number theory). At first glance, however, his work has little to do with prime numbers. He dealt with a specific function, the so-called zeta function ζ( s ), an infinitely long sum that adds the reciprocal values of natural numbers that are raised to the power of s :  Even before Riemann’s work, experts knew that such zeta functions are related to prime numbers. Thus, the zeta function can also be expressed as a function of all prime numbers p as follows:  Riemann recognized the full significance of this connection with prime numbers when he used not only real values for s but also complex numbers. These numbers contain both a real part and roots from negative numbers, the so-called imaginary part. You can imagine complex numbers as a two-dimensional construct. Rather than mark a point on the number line, they instead lie on the plane. The x coordinate corresponds to the real part and the y coordinate to the imaginary part: 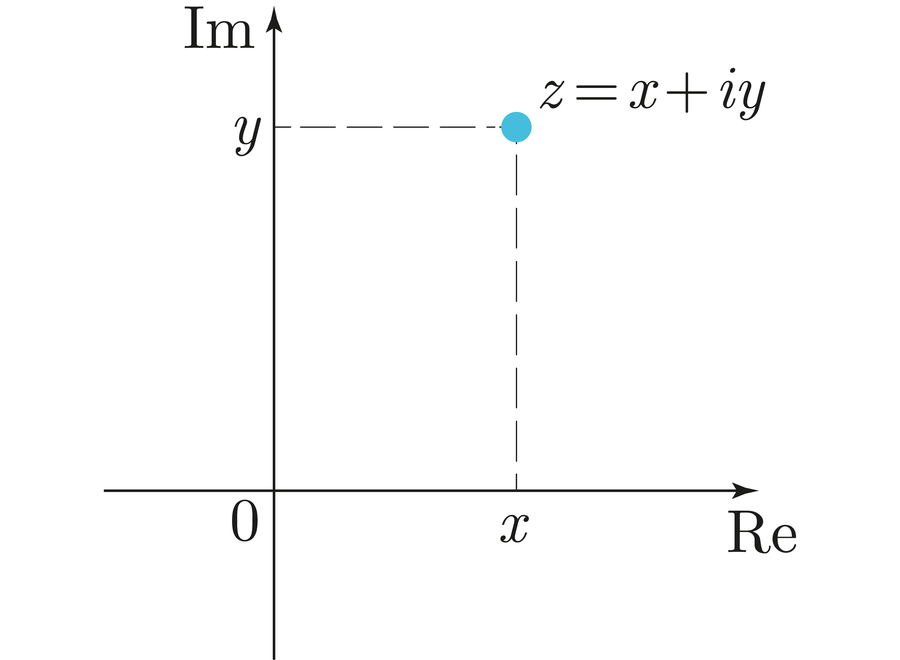 Никита Воробьев/Wikimedia The complex zeta function that Riemann investigated can be visualized as a landscape above the plane. As it turns out, there are certain points amid the mountains and valleys that play an important role in relation to prime numbers. These are the points at which the zeta function becomes zero (so-called zeros), where the landscape sinks to sea level, so to speak.  The colors represent the values of the complex zeta function, with the white dots indicating its zeros. Jan Homann/Wikimedia Riemann quickly found that the zeta function has no zeros if the real part is greater than 1. This means that the area of the landscape to the right of the straight line x = 1 never sinks to sea level. The zeros of the zeta function are also known for negative values of the real part. They lie on the real axis at x = –2, –4, –6, and so on. But what really interested Riemann—and all mathematicians since—were the zeros of the zeta function in the “critical strip” between 0 ≤ x ≤ 1. 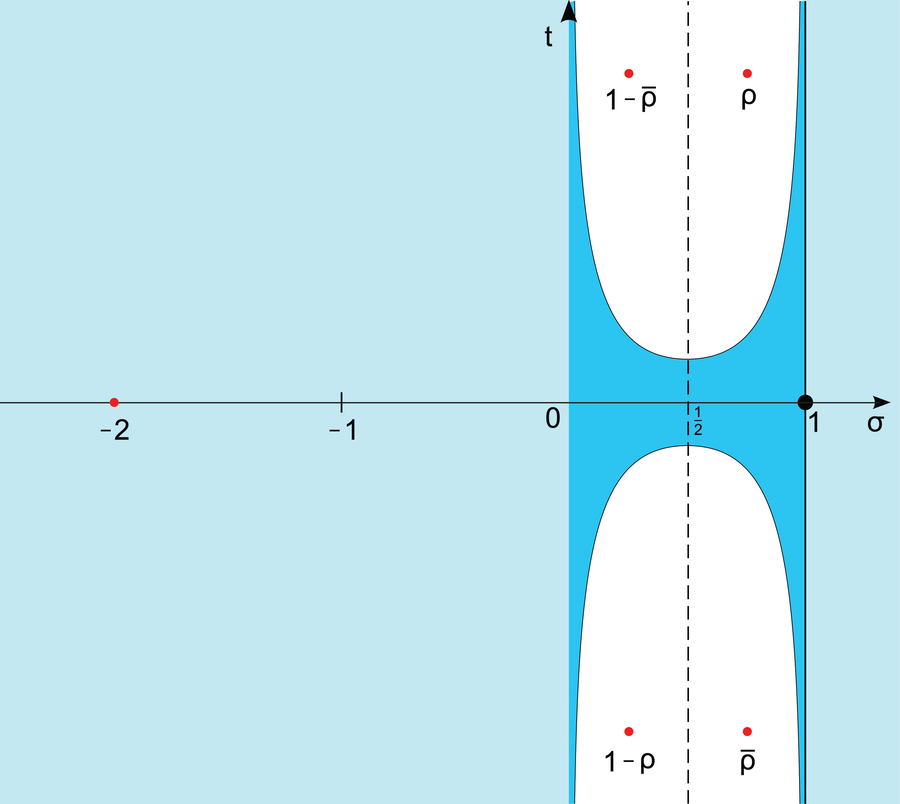 In the critical strip (dark blue), the Riemann zeta function can have “nontrivial” zeros. The Riemann conjecture states that these are located exclusively on the line x = 1/2 (dashed line). LoStrangolatore/Wikimedia ( CC BY-SA 3.0 ) Riemann knew that the zeta function has an infinite number of zeros within the critical strip. But interestingly, all appear to lie on the straight line x = 1 / 2 . Thus Riemann hypothesized that all zeros of the zeta function within the critical strip have a real part of x = 1 / 2 . That statement is actually at the crux of understanding the distribution of prime numbers. If correct, then the placement of prime numbers along the number line never deviates too much from the prime number set. On the Hunt for ZerosTo date, billions and billions of zeta function zeros have now been examined— more than 10 13 of them —and all lie on the straight line x = 1 / 2 . But that alone is not a valid proof. You would only have to find a single zero that deviates from this scheme to disprove the Riemann hypothesis. Therefore we are looking for a proof that clearly demonstrates that there are no zeros outside x = 1 / 2 in the critical strip. Thus far, such a proof has been out of reach, so researchers took a different approach. They tried to show that there is, at most, a certain number N of zeros outside this straight line x = 1 / 2 . The hope is to reduce N until N = 0 at some point, thereby proving the Riemann conjecture. Unfortunately, this path also turns out to be extremely difficult. In 1940 mathematician Albert Ingham was able to show that between 0.75 ≤ x ≤ 1 there are at most y 3/5+ c zeros with an imaginary part of at most y , where c is a constant between 0 and 9. In the following 80 years, this estimation barely improved. The last notable progress came from mathematician Martin Huxley in 1972 . “This has limited us from doing many things in analytic number theory,” Tao wrote in his social media post . For example, if you wanted to apply the prime number theorem to short intervals of the type [ x , x + x θ ], you were limited by Ingham’s estimate to θ > 1 / 6 . Yet if Riemann’s conjecture is true, then the prime number theorem applies to any interval (or θ = 0), no matter how small (because [ x , x + x θ ] = [ x , x + 1] applies to θ = 0). Now Maynard, who was awarded the prestigious Fields Medal in 2022 , and Guth have succeeded in significantly improving Ingham’s estimate for the first time. According to their work, the zeta function in the range 0.75 ≤ x ≤ 1 has at most y (13/25)+ c zeros with an imaginary part of at most y . What does that mean exactly? Blomer explains: “The authors show in a quantitative sense that zeros of the Riemann zeta function become rarer the further away they are from the critical straight line. In other words, the worse the possible violations of the Riemann conjecture are, the more rarely they would occur.” “This propagates to many corresponding improvements in analytic number theory,” Tao wrote . It makes it possible to reduce the size of the intervals for which the prime number theorem applies. The theorem is valid for [ x , x + x 2/15 ], so θ > 1 / 6 = 0.166... becomes θ > 2 ⁄ 15 = 0.133... For this advance, Maynard and Guth initially used well-known methods from Fourier analysis for their result. These are similar techniques to what is used to break down a sound into its overtones. “The first few steps are standard, and many analytic number theorists, including myself, who have attempted to break the Ingham bound, will recognize them,” Tao explained . From there, however, Maynard and Guth “do a number of clever and unexpected maneuvers,” Tao wrote. Blomer agrees. “The work provides a whole new set of ideas that—as the authors rightly say—can probably be applied to other problems. From a research point of view, that’s the most decisive contribution of the work,” he says. So even if Maynard and Guth have not solved Riemann’s conjecture, they have at least provided new food for thought to tackle the 160-year-old puzzle. And who knows—perhaps their efforts hold the key to finally cracking the conjecture. This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission. *Editor’s Note (7/9/24): This sentence was edited after posting to better clarify that prime numbers exclude 1. Plan ahead for the next school year. Schedule your class today ! Something appears to not have loaded correctly. Click to refresh . 
STEM Education
 Solving word problems involving triangles and implications on training pre-service mathematics teachers
Triangles and trigonometry are always difficult topics for both mathematics students and teachers. Hence, students' performance in solving mathematical word problems in these topics is not only a reflection of their learning outcomes but also an indication of teaching effectiveness. This case study drew from two examples of solving word problems involving triangles by pre-service mathematics teachers in a foundation mathematics course delivered by the author. The focus of this case study was on reasoning implications of students' performances on the effective training of pre-service mathematics teachers, from which a three-step interactive explicit teaching-learning approach, comprising teacher-led precise and inspiring teaching (or explicit teaching), student-driven engaged learning (or imitative learning), and student-led and teacher-guided problem-solving for real-world problems or projects (or active application), was summarized. Explicit teaching establishes a solid foundation for students to further their understanding of new mathematical concepts and to conceptualize the technical processes associated with these new concepts. Imitative learning helps students build technical abilities and enhance technical efficacy by engaging in learning activities. Once these first two steps have been completed, students should have a decent understanding of new mathematical concepts and technical efficacy to analyze, formulate, and finally solve real-world applications with assistance from teachers whenever required. Specially crafted professional development should also be considered for some in-service mathematics teachers to adopt this three-step interactive teaching-learning process.
Citation: William Guo. Solving word problems involving triangles and implications on training pre-service mathematics teachers[J]. STEM Education, 2024, 4(3): 263-281. doi: 10.3934/steme.2024016 Related Papers:
SupplementsAccess History
Reader Comments
通讯作者: 陈斌, [email protected]沈阳化工大学材料科学与工程学院 沈阳 110142  Article views( 66 ) PDF downloads( 5 ) Cited by( 0 ) Figures and Tables Figures( 5 ) / Tables( 3 )  Associated materialOther articles by authors.
Related pages
Export File
Help | Advanced Search Computer Science > Artificial IntelligenceTitle: solving for x and beyond: can large language models solve complex math problems with more-than-two unknowns. Abstract: Large Language Models (LLMs) have demonstrated remarkable performance in solving math problems, a hallmark of human intelligence. Despite high success rates on current benchmarks; however, these often feature simple problems with only one or two unknowns, which do not sufficiently challenge their reasoning capacities. This paper introduces a novel benchmark, BeyondX, designed to address these limitations by incorporating problems with multiple unknowns. Recognizing the challenges in proposing multi-unknown problems from scratch, we developed BeyondX using an innovative automated pipeline that progressively increases complexity by expanding the number of unknowns in simpler problems. Empirical study on BeyondX reveals that the performance of existing LLMs, even those fine-tuned specifically on math tasks, significantly decreases as the number of unknowns increases - with a performance drop of up to 70\% observed in GPT-4. To tackle these challenges, we propose the Formulate-and-Solve strategy, a generalized prompting approach that effectively handles problems with an arbitrary number of unknowns. Our findings reveal that this strategy not only enhances LLM performance on the BeyondX benchmark but also provides deeper insights into the computational limits of LLMs when faced with more complex mathematical challenges.
Submission historyAccess paper:.
References & Citations
BibTeX formatted citationBibliographic and Citation ToolsCode, data and media associated with this article, recommenders and search tools.
arXivLabs: experimental projects with community collaboratorsarXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website. Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them. Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .  Game Central |
IMAGES
VIDEO
COMMENTS
Online math solver with free step by step solutions to algebra, calculus, and other math problems. Get help on the web or with our math app.
Free Pre-Algebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators step-by-step
Online math solver with free step by step solutions to algebra, calculus, and other math problems. Get help on the web or with our math app.
QuickMath allows students to get instant solutions to all kinds of math problems, from algebra and equation solving right through to calculus and matrices.
Get accurate solutions and step-by-step explanations for algebra and other math problems with the free GeoGebra Math Solver. Enhance your problem-solving skills while learning how to solve equations on your own. Try it now!
Free math problem solver answers your algebra homework questions with step-by-step explanations.
Symbolab is an AI-powered math calculator that provides step-by-step solutions to algebra, trigonometry, and calculus problems.
Solve your math problems using our free math solver with step-by-step solutions. Our math solver supports basic math, pre-algebra, algebra, trigonometry, calculus and more.
Algebra (all content) | Khan Academy. 20 units · 412 skills. Unit 1 Introduction to algebra. Unit 2 Solving basic equations & inequalities (one variable, linear) Unit 3 Linear equations, functions, & graphs. Unit 4 Sequences. Unit 5 System of equations. Unit 6 Two-variable inequalities. Unit 7 Functions.
Math strategies for problem solving help students define the problem and highlight the key information to help them find a solution.
That's because Khan Academy has over 100,000 free practice questions. And they're even better than traditional math worksheets - more instantaneous, more interactive, and more fun!
This online Math solver can tell you the answer for your math problem or word problem, and even show you the steps.
Becoming confident and competent as a problem solver is a complex process that requires a range of skills and experience. In this article, Jennie suggests that we can support this process in three principal ways. This article, written for primary teachers, discusses what we mean by 'problem-solving skills' and draws attention to NRICH tasks ...
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with step-by-step explanations, just like a math tutor.
Even simple math problems become easier to solve when broken down into steps. From basic additions to calculus, the process of problem solving usually takes a lot of practice before answers could come easily. As problems become more complex, it becomes even more important to understand the step-by-step process by which we solve them.
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. For math, science, nutrition, history ...
MathGPT is an AI-powered math problem solver, integral calculator, derivative cacluator, polynomial calculator, and more! Try it out now and solve your math homework!
Unlock the power of math AI with Mathful, your ultimate photo math solver and calculator with steps. It offers accurate solutions to all your math problems.
Math Solver achieves 92% accuracy in solving math problems by leveraging code interpreters, with support from ChatGPT and GPT-4.
The Millennium Prize Problems are seven well-known complex mathematical problems selected by the Clay Mathematics Institute in 2000. The Clay Institute has pledged a US$ 1 million prize for the first correct solution to each problem.
Imagination is how we go from just solving problems to posing even more ambitious questions and moving forwards. "What's really special about NRICH is that we encourage children to problem solve in different ways, take different approaches, and use and apply their maths.
Mathematicians are often haunted by problems that elude solutions and take centuries of effort to solve. Here we review 7 of the hardest math problems ever solved.
In new research, mathematicians have narrowed down one of the biggest outstanding problems in math. Huge breakthroughs in math and science are usually the work of many people over many years ...
Get free step-by-step solutions for algebra math problems with the Symbolab Number Line Algebra Calculator.
The Riemann hypothesis is the most important open question in number theory—if not all of mathematics. It has occupied experts for more than 160 years. And the problem appeared both in ...
Small live classes for advanced math and language arts learners in grades 2-12.
Triangles and trigonometry are always difficult topics for both mathematics students and teachers. Hence, students' performance in solving mathematical word problems in these topics is not only a reflection of their learning outcomes but also an indication of teaching effectiveness. This case study drew from two examples of solving word problems involving triangles by pre-service mathematics ...
Large Language Models (LLMs) have demonstrated remarkable performance in solving math problems, a hallmark of human intelligence. Despite high success rates on current benchmarks; however, these often feature simple problems with only one or two unknowns, which do not sufficiently challenge their reasoning capacities. This paper introduces a novel benchmark, BeyondX, designed to address these ...
Online math solver with free step by step solutions to algebra, calculus, and other math problems. Get help on the web or with our math app.
A fashion major from a vocational high school in rural China has amazed the nation by outshining elite students in a global math contest - but the teenager's underdog story has now been mired ...