
Group Theory
Explore groups through symmetries, applications, and problems.
Come to know mathematical groups through symmetry.
Combining Symmetries
Gain a visual understanding of how groups work.
- Group Axioms
What makes a set into a group?
Cube Symmetries
Explore group axioms with cube symmetries.
End of Unit 1
Complete all lessons above to reach this milestone.
0 of 4 lessons complete
Axioms and Basic Examples
Dive deeper into groups by exploring some real-world applications.
More Group Examples
See how groups tie into geometry and music.
Learn about the structure of groups within a group.
- Abelian Groups
For these groups, composition order doesn't matter.
- Homomorphisms
Play with group functions that preserve the groups' structures.
- Quotient Groups
It's a bit like factoring groups...
End of Unit 2
0 of 6 lessons complete
Number Theory
Use groups to unlock the secrets of integers.
Puzzle Games
Formulate winning game strategies with groups!
Rubik's Cubes
Apply groups to understand this perplexing toy.
End of Unit 3
0 of 3 lessons complete
Normal Subgroups
Explore normality, a critical ingredient in making quotient groups.
Isomorphism Theorems
When are two groups different versions of the same thing?
- Conjugacy Classes
Learn a wealth of information about a group by separating its elements by class.
The Symmetric Group
Master the fundamentals of permutations.
Signs of Permutations
Connect the Legendre symbol from number theory to permutation signs.
End of Unit 4
0 of 5 lessons complete
- Group Actions
Explore the interplay between a group and the set it acts upon.
Burnside's Lemma
Solve challenging counting and combinatorial problems with group theory.
Semidirect Products
Learn a useful technique for building larger groups from smaller ones.
- Sylow Theorems
Explore the structure of finite groups and uncover fascinating new relations.
End of Unit 5
Course description.
This course was written in collaboration with Jason Horowitz, who received his mathematics PhD at UC Berkeley and was a founding teacher at the mathematics academy Proof School. This course explores group theory at the university level, but is uniquely motivated through symmetries, applications, and challenging problems. For example, before diving into the technical axioms, we'll explore their motivation through geometric symmetries. You'll be left with a deep understanding of how group theory works and why it matters.
Topics covered
- Direct and Semidirect Products
- Isomorphisms
- Normal Groups
Prerequisites and next steps
Familiarity with linear algebra basics and a willingness to engage with mathematical abstraction is all that’s required!
Prerequisites

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

13: The Structure of Groups
- Last updated
- Save as PDF
- Page ID 81131

- Thomas W. Judson
- Stephen F. Austin State University via Abstract Algebra: Theory and Applications
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
The ultimate goal of group theory is to classify all groups up to isomorphism; that is, given a particular group, we should be able to match it up with a known group via an isomorphism. For example, we have already proved that any finite cyclic group of order \(n\) is isomorphic to \({\mathbb Z}_n\text{;}\) hence, we “know” all finite cyclic groups. It is probably not reasonable to expect that we will ever know all groups; however, we can often classify certain types of groups or distinguish between groups in special cases.
In this chapter we will characterize all finite abelian groups. We shall also investigate groups with sequences of subgroups. If a group has a sequence of subgroups, say
\[ G = H_n \supset H_{n - 1} \supset \cdots \supset H_1 \supset H_0 = \{ e \}\text{,} \nonumber \]
where each subgroup \(H_i\) is normal in \(H_{i+1}\) and each of the factor groups \(H_{i+1}/H_i\) is abelian, then \(G\) is a solvable group. In addition to allowing us to distinguish between certain classes of groups, solvable groups turn out to be central to the study of solutions to polynomial equations.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

Group Theory and its Application to Chemistry
- Last updated
- Save as PDF
- Page ID 1890
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Group Theory is the mathematical application of symmetry to an object to obtain knowledge of its physical properties. What group theory brings to the table, is how the symmetry of a molecule is related to its physical properties and provides a quick simple method to determine the relevant physical information of the molecule. The symmetry of a molecule provides you with the information of what energy levels the orbitals will be, what the orbitals symmetries are, what transitions can occur between energy levels, even bond order to name a few can be found, all without rigorous calculations. The fact that so many important physical aspects can be derived from symmetry is a very profound statement and this is what makes group theory so powerful.
Introduction
To a fully understand the math behind group theory one needs to take a look at the theory portion of the Group Theory topic or refer to one of the reference text listed at the bottom of the page. Never the less as Chemist the object in question we are examining is usually a molecule. Though we live in the 21 st century and much is known about the physical aspects that give rise to molecular and atomic properties. The number of high level calculations that need to be performed can be both time consuming and tedious. To most experimentalist this task is takes away time and is usually not the integral part of their work. When one thinks of group theory applications one doesn't necessarily associated it with everyday life or a simple toy like a Rubik's cube. A Rubik's cube is an a cube that has a \(3 \times 3\) array of different colored tiles on each of its six surfaces, for a total of 54 tiles. Since the cube exist in 3D space, the three axis are \(x\), \(y\), \(z\). Since the rubik's cube only allows rotation which are called operations, there are three such operations around each of the \(x\), \(y\), \(z\) axis.

Of course the ultimate challenge of a Rubik's cube is to place all six colors on each of the six faces. By performing a series of such operations on the Rubik's cube one can arrive at a solution (A link of a person solving a Rubik's cube 1 in 10.4s with operations performed noted, the operations performed will not translate to chemistry applications but it is a good example of how symmetry operations arrive at a solution). The operations shown in the Rubik's cube case are inherent to the make up of the cube, i.e., the only operations allowed are the rotations along the x, y, z axis. Therefore the Rubik's cube only has x,y,z rotation operations. Similarly the operations that are specific to a molecule are dependent on its symmetry. These operations are given in the top row of the character table.
| \(C_{3v}\) | \(E\) | \(2C_3\) | \(3\sigma_v\) | ||
|---|---|---|---|---|---|
| \(A_1\) | +1 | +1 | +1 | \(z\) | \(x^2+y^2\), \(z^2\) |
| \(A_2\) | +1 | +1 | -1 | \(R_z\) | - |
| \(E\) | +2 | -1 | 0 | (\(x\), \(y\)) (\(R_x\), \(R_y\)) | (\(x^2-y^2\), \(xy\)) (\(xz\), \(yz\)) |
The character table contains a wealth of information, for a more detailed discussion of the character table can be found in Group Theory Theoretical portion of the chemWiki. All operations in the character table are contained in the first row of the character table, in this case \(E\), \(C_3\), & \(\sigma_v\), these are all of the operations that can be preformed on the molecule that return the original structure. The first column contains the three irreducible representations from now on denoted as \(\Gamma_{ir}\), here they are \(A_1\), \(A_2\) & \(E\). The value of the \(\Gamma_{ir}\) denotes what the operation does. A value of 1 represents no change, -1 opposite change and 0 is a combination of 1 & -1 (0’s are found in degenerate molecules. The final two columns Rotation and Translation represented by \(R_x\),\(R_y\), \(R_z\) & \(x\), \(y\), \(z\) respectively. Where R's refer to rotation about an axis and the \(x\), \(y\), \(z\) refers to a translation about an axis, the \(\Gamma_{ir}\) the each \(R_x\), \(R_y\), \(R_z\) & \(x\), \(y\), \(z\) term is the irreducible symmetry of a rotation or translation operation. Like wise the final column the orbital symmetries relates the orbital wavefunction to a irreducible representation.
Direct Products
This is a quick rule to follow for calculating Direct Products of irreproducible representations, such a calculation will be necessary for working through transition moment integrals. Following the basic rules given by the table given below. One can easily work through symmetry calculations very quickly.
| "Symmetric" \(\times\) "Symmetric" is "Symmetric" | "Symmetric" \(\times\) "AntiSymmetric" is "AntiSymmetric" | "AntiSymmetric" \(\times\) "Symmetric" is "AntiSymmetric" | "AntiSymmetric" \(\times\) "AntiSymmetric" is "Symmetric" |
|---|---|---|---|
| \(g \times g = g\) | \(g \times u = u\) | \(u \times g = u\) | \(u \times u = g\) |
| \( ' \times ' = '\) | \( ' \times '' = ''\) | \( '' \times ' = ''\) | \( '' \times '' = '\) |
| \(A \times A= A\) | \(A \times B= B\) | \(B \times A= B\) | \(B \times B= A\) |
All molecules vibrate. While these vibrations can originate from several events, which will be covered later, the most basic of these occurs when an electron is excited within the electronic state from one eigenstate to another. The Morse potential (electronic state) describes the energy of the eigenstate as a function of the interatomic distance. When an electron is excited form one eigenstate to another within the electronic state there is a change in interatomic distance, this result in a vibration occurring.
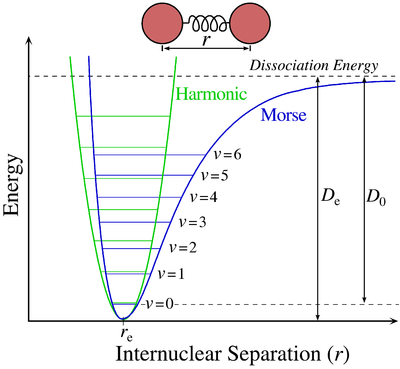
Vibrational energies arise from the absorption of polarizing radiation. Each vibrational state is assigned a \(\Gamma_{ir}\). A vibration occurs when an electron remains within the electronic state but changes from one eigenstate to another (The vibrations for the moment are only IR active vibrations, there are also Raman vibrations which will be discussed later in electronic spectroscopy), in the case of the Morse diagram above the eigenstates are denoted as \(\nu\). As you can see from the diagram the eigenstate is a function of energy versus interatomic distance.
To predicting whether or not a vibrational transition, or for that matter a transition of any kind, will occur we use the transition moment integral.
\[\int \Psi_i*\mu \Psi_f d\tau=\langle \Psi_i | \mu| \Psi_f \rangle\]
The transition moment integral is written here in standard integral format, but this is equivalent to Bra & Ket format which is standard in most chemistry quantum mechanical text (The \(\langle \Psi_i |\) is the Bra portion, \(| \Psi_f \rangle\) is the Ket portion). The transition moment operator \(\mu\) is the operator the couples the initial state \(\Psi_i\) to the final state \(\Psi_f\), which is derived from the time independent Schrödinger equation. However using group theory we can ignore the detailed mathematical methods. We can use the \(\Gamma_{ir}\) of the vibrational energy levels and the symmetry of the transition moment operator to find out if the transition is allowed by selection rules. The selection rules for vibrations or any transition is that is allowed, for it to by allowed by group theory the answer must contain the totally symmetric \(\Gamma_{ir}\) , which is always the first \(\Gamma_{ir}\) in the character table for the molecule in question.
Let’s work through an example: Ammonia (\(NH_3\)) with a \(C_{3v}\) symmetry. Consequently, all of the properties contained in the \(C_{3v}\) character table above are pertinent to the ammonia molecule.
The principle axis is the axis that the highest order rotation can be preformed. In this case the z-axis pass through the lone pairs (pink sphere), which contains a \(C_3\) axis. The ?’s or mirror planes (\(\sigma_v\) parallel to z-axis & \(\sigma_h\) perpendicular to the z-axis). In ammonia there is no \(\sigma_h\) only three \(\sigma_v\)’s. The combination of \(C_3\) & \(\sigma_v\) leads to \(C_{3v}\) point group, which leads to the C3v character table.
The number of transitions is dictated by 3N-6 for non-linear molecules and 3N-5 for linear molecules, where N is the number of atoms. The 6 & the 5 derive from three translations in the x,y,z plan and three rotations also in the x,y,z plan. Where a linear molecule only has two rotations in the x & y plans since the z axis has infinite rotation. This leads to only 5 degrees of freedom in the rotation and translation operations. In the case of Ammonia there will be 3(4)-6=6 vibrational transitions. This can be confirmed by working through the vibrations of the molecule. This work is shown in the table below.
The vibrations that are yielded 2A1 & 2E (where E is doubly degenerate, meaing two vibration modes each) which total 6 vibrations. This calculation was done by using the character table to find out the rotation and translation values and what atoms move during each operation. Using the character table we can characterize the A1 vibration as IR active along the z-axis and raman active as well. The E vibration is IR active along both the x & y axis and is Raman active as well. From the character table the IR symmetries correspond to the x, y & z translations. Where the Raman active vibrations correspond to the symmetries of the d-orbitals.
Vibrational Spectroscopy
Infrared spectroscopy.
Infrared Spectroscopy (IR) measures the vibrations that occur within a single electronic state, such as the one shown above. Because the transition occurs within a single electronic state there is a variation in interatomic distance. The dipole moment is dictate by the equation.
\[ \vec{\mu} = \alpha\vec{E} \]
Where \( \vec{\mu} \) is the magnitude of dipole moment; \( \alpha \) is the polarizability constant (actually a tensor) & \( E \) is the magnitude of the electric field which can be described as the electronegitivity. 3 Therefore when a vibration occurs within a single electronic state there is a change in the dipole moment, which is the definition of an active IR transition.
\[ \left ( \frac{\mathrm{d\mu} }{\mathrm{d} q} \right )_{eq} \neq 0 \]
In terms of group theory a change in the dipole is a change from one vibrational state to another, as shwon by the equation above. A picture of the vibrational states with respect ot the rotational states and electronic states is given below. In IR spectroscopy the transition occurs only from on vibrational state to another all within the same electronic state, shown below as B.
.jpg?revision=1&size=bestfit&width=572&height=414)
Where group theory comes in to play is weather or not this transition is allowed by symmetry. This can be determined by the transition moment integral described above. For example if one works through a transition from the ground vibrational state, which is always the totally symmetric in this example A 1g , to a excited vibrational state, B 2u . The possible symmetries for the transition moment operator are A 1g ,B 2u ,B 2g , for x,y,z transitions repectively (one obtains the transition moment operator from the character table for the ?ir of the x,y,z translations) .
<A 1g lMlB 2u >, M=A 1g ,B 2u or B 2g
From the direct product rules one can work through each of the transiton moment operators and see if the awnser contains the totally symmetric ?ir. The first direct product gives a A 1g xA 1g xB 2u =B 2u , so this transition is not x polarized. The y polarized transition moment operator gives A 1g xB 2u xB 2u =A 1g , this transition is allowed by symmetry. The final polarization z, gives A 1g xB 2g xB 2u =A 1u , this transition is also not allowed by symmetry. So this IR transition is allowed by y polarized light in this molecule.
Electronic Transitions
When an electron is excited from one electronic state to another, this is what is called an electronic transition. A clear example of this is part C in the energy level diagram shown above. Just as in a vibrational transition the selection rules for electronic transitions are dictated by the transition moment integral. However we now must consider both the electronic state symmetries and the vibration state symmetries since the electron will still be coupled between two vibrational states that are between two electronic states. This gives us this modified transition moment integral:
Where you can see that the symmetry of the initial electronic state & vibrational state are in the Bra and the final electronic and vibrational states are in the Ket. Though this appears to be a modified version of the transition moment integral, the same equation holds true for a vibrational transition. The only difference would be the electronic state would be the same in both the initial and final states. Which the dot product of yields the totally symmetric representation, making the electronic state irrelevant for purely vibrational spectroscopy.
In Resonance Raman spectroscopy transition that occurs is the excitation from one electronic state to another and the selection rules are dictated by the transition moment integral discussed in the electronic spectroscopy segment. However mechanically Raman does produce a vibration like IR, but the selection rules for Raman state there must be a change in the polarization, that is the volume occupied by the molecule must change. But as far as group theory to determine whether or not a transition is allowed one can use the transition moment integral presented in the electronic transition portion. Where one enters the starting electronic state symmetry and vibrational symmetry and final electronic state symmetry and vibrational state, perform the direct product with the different M's or polarizing operators For more information about this topic please explore the Raman spectroscopy portion of the Chemwiki
Fluorescence
For the purposes of Group Theory Raman and Fluorescence are indistinguishable. They can be treated as the same process and in reality they are quantum mechanically but differ only in how Raman photons scatter versus those of fluorescence.
Phosphorescence
Phosphorescence is the same as fluorescence except upon excitation to a singlet state there is an interconversion step that converts the initial singlet state to a triplet state upon relaxation. This process is longer than fluorescence and can last microseconds to several minutes. However despite the singlet to triplet conversion the transition moment integral still holds true and the symmetry of ground state and final state still need to contain the totally symmetric representation.
Molecular Orbital Theory and Symmetry
Molecular Orbitals also follow the symmetry rules and indeed have their own ?ir. Below are the pi molecular orbitals for trans-2-butene and the corresponding symmetry of each molecular orbital.
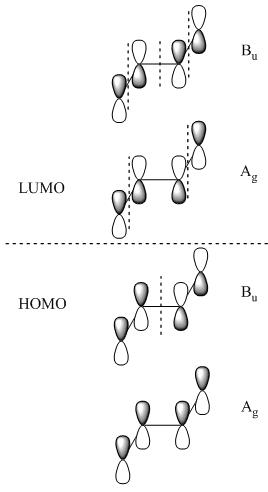
The ?ir of the molecular orbitals are created by simply preforming the operations of that molecule's character table on that orbital. In the case of trans-2-butene the point group is C2h, the operations are: E, C2, i & ?h. Each operation will result in a change in phase (since were dealing with p-orbitals) or it will result in no change. The first molecular orbital results in the totally symmetric representation, working through all four operations E, C2, i, ?h will only result in 1's meaning there is no change, giving the Ag symmetry state. These molecular orbitals also represent different electronic states and can be arranged energetically. Putting the orbital that has the lowest energy, the orbital with the fewest nodes at the bottom of the energy diagram and like wise working up form lowest energy to highest energy. The highest energy orbital will have the most nodes. Once you've set up your MO diagram and place the four pi electrons in the orbitals you see that the first two orbitals listed (lowest energy) are HOMO orbitals and the bottom two (highest energy) and LUMO orbitals. With this information if you have a transition from the totally symmetric HOMO orbital to the totally symmetric LUMO orbital the transition moment operator would need to have Ag symmetry (using the C2h) to give a result containing the totally symmetric representation.
These four molecular orbitals represent four different electronic states. So transitions from one MO into another would be something that is measured typically with UV-Vis spectrometer.
References and Further Reading
- Daniel Harris & Michael Bertolucci Symmetry and Spectroscopy New York, Dover Publications 1989 ($19.95), [Highly recommended, great text for explaining Group Theory for molecules and Application of Group Theory in various spectroscopy's]
- Albert Cotton Chemical Applications of Group Theory 3rd New York, Wiley Inter-science Publication 1990 ($148.50),[Mathematical approach to group theory in chemistry]
- Donald A. McQuarrie Quantum Chemistry Sausalito, University Science Books 1983 ($88.00) [Classic Quantum chemistry text very clear and thorough]
- Douglas Skoog, James Holler & Stanley Crouch Principles of Instrumental Analysis (6th ed) Thomson Brooks Cole 2007 ($170.04), [Covers basics of all types of analytical chemistry methods and theory]
- Follow the links above to Water, Ammonia and Benzene and work out the ?ir of the vibrations. Using the method laid out by the character table. (Follow the example of ammonia for help)
- From problem 1. work out what possible are the possible transition moment operators for each vibration.
- Work through the P-orbital molecular orbitals for cis-butadiene. (Note the conservation of "stuff", start by combining four p-orbitals and finish with four molecular orbitals) What is the point group? what are the ? ir of each MO? Finally how many vibrations are there for cis-butadiene and what are their ?ir.
Due: Thursday, March 6, 00:00AM
Group Theory
In this assignment, you will prove several simple theorems of Group Theory, which you might have studied in an undergraduate abstract algebra course. If you didn’t take abstract algebra, you missed out on some wonderful mathematics, but this is your chance to learn some of the basics. You could look up group theory on Wikipedia or look it up in a book. I enjoyed Contemporary Abstract Algebra by Joseph Gallian, which is available at the UMass library.
Requirements
For the purposes of this assignment, a group is a set G , an associative binary operator f over G , an identity element e of G , and a unary inverse function i for G. The following types, which you must use, define a group and its basic axioms in Coq:
Your task is to use the definitions above to prove all the theorems below:
There is a wrinkle: every theorem or lemma must be proved by either a single call to crush or a single call to eauto! You may pass a numeric argument to eauto to control the search depth. Some theorems and lemmas may be necessary to prove subsequent theorems. You can add these as hints using Hint Resolve .
One more use of tactics is allowed in this problem. The following lemma captures a common pattern of reasoning in algebra proofs:
That is, we know some equality a = b , which is the third hypothesis above. We derive a further equality by multiplying both sides by c , to yield a <+> c = b <+> c . Next, we do algebraic simplification on both sides of this new equality, represented by the first two hypotheses above. The final result is a new theorem of algebra.
Chapter 14 of CPDT introduces more details of programming in Ltac, but here is a quick teaser that will be useful in this problem. Include the following hint command before you start proving the main theorems of this exercise:
This hint has the effect of applying mult_both at most once during a proof. After reading Chapter 14, it should be clear why the hint has that effect, but for now treat it as a useful black box. Simply using Hint Resolve mult_both would increase proof search time unacceptably, because there are just too many ways to use mult_both repeatedly within a proof.
I recommend proving the theorems in roughly the order written above. There are some dependencies between the theorems too. For example, it is helpful to have Hint Resolve unique_id before trying to prove inv_l . You only need to use Hint Resolve . There is no need for Hint Rewrite , Hint Immediate , etc.
The following web page has informal proofs of some of the first theorems you need to prove:
http://dogschool.tripod.com/housekeeping.html
You should start by formalizing them.
You can write eauto N , where N sets the depth of proof search. The default is eauto 5 , which can be quite slow. Lower values will make proof search go faster when a proof exists within the bound. Higher values are necessary to find more involved proofs. Most proofs should be found with eauto 3 or eauto 4 .
The key to this problem is coming up with further lemmas like mult_both that formalize common patterns of reasoning in algebraic proofs. These lemmas need to be more than sound: they must also fit well with the way that eauto does proof search. For instance, if we had given mult both a traditional statement, we probably would have avoided “pointless” equalities like a = b , which could be avoided simply by replacing all occurrences of b with a. However, the resulting theorem would not work as well with automated proof search! Every additional hint you come up with should be registered with Hint Resolve, so that the lemma statement needs to be in a form that eauto understands natively.
I recommend testing a few simple rules corresponding to common steps in algebraic proofs. You can apply them manually with any tactics you like (e.g., apply or eapply ) to figure out what approaches work, and then switch to eauto once you have the full set of hints.
Acknowledgments
This assignment is derived from Exercise 0.8.1 of Adam Chlipala’s online CPDT exercises .
MacTutor
The development of group theory.
- geometry at the beginning of the 19 th Century,
- number theory at the end of the 18 th Century,
- the theory of algebraic equations at the end of the 18 th Century leading to the study of permutations.
References ( show )
- B Chandler and W Magnus, The history of combinatorial group theory : A case study in the history of ideas ( New York-Berlin, 1982) .
- R Franci, On the axiomatization of group theory by American mathematicians : 1902 - 1905 , Amphora ( Basel, 1992) , 261 - 277 .
- J Gray, Otto Hölder and group theory, Math. Intelligencer 16 (3) (1994) , 59 - 61 .
- B M Kiernan, The development of Galois theory from Lagrange to Artin, Archive for History of Exact Sciences 8 (1971) , 40 - 154 .
- I Kleiner, The evolution of group theory : a brief survey, Mathematics magazine 59 (4) (1986) , 195 - 215 .
- J J Nicholson, Otto Holder and the Development of Group Theory and Galois Theory ( Ph.D. Thesis Oxford, 1993) .
- L Novy, Origins of Modern Algebra ( Prague, 1973) .
- K V H Parshall, A study in group theory : Leonard Eugene Dickson's 'Linear groups', Math. Intelligencer 13 (1) (1991) , 7 - 11 .
- H Wussing, The Genesis of the Abstract Group Concept ( Cambridge, MA., 1984) .

Course Name: Group Theory Methods in Physics
- About Course
- Certificate Type
- Toppers list
- Registration
Course abstract
This course is a first course pitched at UG level so that the students can appreciate the wide applications of the group theory tools in other areas of physics
Course Instructor

Prof. P. Ramadevi
Teaching assistant(s).

Aman Awasthi

Adiba Shaikh
Course Duration : Jan-Apr 2020
view course, syllabus, enrollment : 18-nov-2019 to 03-feb-2020, exam registration : 16-dec-2019 to 21-feb-2020, exam date : 26-apr-2020, course statistics will be published shortly, certificate eligible, certified category count, successfully completed, participation.
.jpg)
Category : Successfully Completed
.jpg)
Category : Elite
.jpg)
Category : Silver
.jpg)
Category : Gold
Final score calculation logic.
- Assignment Score = Average of best 8 out of 12 assignments.
- Final Score(Score on Certificate)= 75% of Exam Score + 25% of Assignment Score

ANIRBAN DASGUPTA 83%
NATIONAL INSTITUTE OF TECHNOLOGY, JAMSHEDPUR
Enrollment Statistics
Total enrollment: 948, registration statistics, total registration : 49, assignment statistics, score distribution graph - legend, assignment score: distribution of average scores garnered by students per assignment., exam score : distribution of the final exam score of students., final score : distribution of the combined score of assignments and final exam, based on the score logic..






IMAGES
VIDEO
COMMENTS
MATH 3175 2 Homework 1 Solutions. Karthik B. Group Theory Dr. Suciu. (b) The condition f(x) = z; which holds true for all z 2C precisely when f is surjective (there exists a suitable x), is equivalent to the condition f(x) z = 0: Because z is a constant, f(x) z is again a polynomial with complex coe cients. By the fact that C is algebraically ...
2.7. Let Gbe nite non-abelian group of order nwith the property that Ghas a subgroup of order kfor each positive integer kdividing n. Prove that Gis not a simple group. Solution Let jGj= nand pbe the smallest prime dividing jGj. If Gis a p-group, then 1 6= Z(G) G. Hence Gis not simple. So we may assume that Ghas composite order. Then by ...
The group table completely specifies the group. 1.11. Theorem. In a group table, every group element appears precisely once in ev-ery row, and once in every column. Proof. Suppose in the ith row we have x ix j= x ix kfor j6=k. Multiplying from the left by x-1 i we obtain x j= x k, which contradicts our assumption that x jand x kare distinct ...
Group theory is the study of groups. Groups are sets equipped with an operation (like multiplication, addition, or composition) that satisfies certain basic properties. As the building blocks of abstract algebra, groups are so general and fundamental that they arise in nearly every branch of mathematics and the sciences. For example: Symmetry groups appear in the study of combinatorics ...
The element e2Gis referred to as the identity of the group. The map mis referred to as the multiplication law, or the group law. Let us now see some examples of groups. Example 1.3.2. We have already seen this example of a group. Let Xbe a set. De ne m: Aut(X) Aut(X) !Aut(X) by m(f;g) := f g. Then the triple (Aut(X);m;Id X) is a group. This is the
NOTES ON GROUP THEORY Abstract. These are the notes prepared for the course MTH 751 to be o ered to the PhD students at IIT Kanpur. Contents 1. Binary Structure 2 2. Group Structure 5 3. Group Actions 13 4. Fundamental Theorem of Group Actions 15 5. Applications 17 5.1. A Theorem of Lagrange 17 5.2. A Counting Principle 17 5.3. Cayley's ...
Group Actions. This course was written in collaboration with Jason Horowitz, who received his mathematics PhD at UC Berkeley and was a founding teacher at the mathematics academy Proof School. This course explores group theory at the university level, but is uniquely motivated through symmetries, applications, and challenging problems.
An assignment on a non empty set G is a map :G×G→G, (a,b)→a b that assigns to each pair (a,b)of elements of the set G another element a b of G. A group G is a set G together with an assignment such that the following three properties hold: (1) The assignment is associative, thatmeans thatfor every three elementsa,b,c in G the identity
Karthik B. Group Theory Dr. Suciu Group Theory Homework 2 Solutions Karthik Boyareddygari Professor Alexandru Suciu Problem 1: (i) First of all, H as de ned is nonempty because e3 = e always. Now suppose that a;b 2H are arbitrary elements. Because G is Abelian, we nd that (ab 1)3 = ab 1ab 1ab 1 = a3b 3 = e(b3) 1 = ee 1 = e =)ab 1 2H: Therefore ...
The set of integers (positive, negative and zero) is an Abelian group of infinite order where the common addition plays the role of multiplication. Zero serves as the unit and the inverse of a is −a − a. Example 1.1.2 1.1. 2. The set of permutations of n objects, called also the symmetric group S(n) S ( n), is of order n! n!.
81131. Thomas W. Judson. Stephen F. Austin State University via Abstract Algebra: Theory and Applications. The ultimate goal of group theory is to classify all groups up to isomorphism; that is, given a particular group, we should be able to match it up with a known group via an isomorphism. For example, we have already proved that any finite ...
Group Theory and its Application to Chemistry is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Jim Hughes. Group Theory is the mathematical application of symmetry to an object to obtain knowledge of its physical properties. What group theory brings to the table, is how the symmetry of a molecule is ….
1.1.2 The basic idea of a group The essential di erence between a monoid and a group is that, in the latter, every element has an inverse. This property is of fundamental signi cance for the applicability of group theory to physics, and is formalized in the following de nition. De nitions. 1.
In this series, Sagar Surya will conduct a session on Group Theory Assignment. The series will be beneficial for strengthening the basic concepts of Calculus...
For the purposes of this assignment, a group is a set G, an associative binary operator f over G, an identity element e of G, and a unary inverse function i for G. The following types, which you must use, define a group and its basic axioms in Coq: (* The set of the group. *) Parameter G : Set. (* The binary operator. *) Parameter f : G -> G -> G.
The three main areas that were to give rise to group theory are:-. geometry at the beginning of the 19th Century, number theory at the end of the 18th Century, the theory of algebraic equations at the end of the 18th Century leading to the study of permutations. (1) Geometry has been studied for a very long time so it is reasonable to ask what ...
AVERAGE ASSIGNMENT SCORE >=10/25 AND EXAM SCORE >= 30/75 AND FINAL SCORE >=40 BASED ON THE FINAL SCORE, Certificate criteria will be as below: >=90 - Elite + Gold ... Group Theory Methods in Physics - Toppers list. ANIRBAN DASGUPTA 83%. NATIONAL INSTITUTE OF TECHNOLOGY, JAMSHEDPUR. Enrollment Statistics. Total Enrollment: 948.
Introduction to Abstract Group Theory. This course will introduce abstract groups. We will start with definitions, basic properties and constructions and cover many important theorems in basic group theory, such as Lagrange's theorem, Cauchy's theorem and Sylow theorems. A major emphasis of the course will be to present numerous worked-out ...
Applications of. group theory. Galois theory arose in direct connection with the study of polynomials, and thus the notion of a group developed from within the mainstream of classical algebra. However, it also found important applications in other mathematical disciplines throughout the 19th century, particularly geometry and number theory.
The course introduces some of the basic ideas of Group Theory, including symmetry groups, abelian, cyclic, and permutation groups, as well as subgroups, normal subgroups, group homomorphisms, quotient groups, direct products, group actions on a set, and the Sylow theorems. ... Based on homework assignments (50%), midterm exam (20%), and final ...
Group theory is the branch of mathematics that includes the study of elements in a group. Group is the fundamental concept of algebraic structure like other algebraic structures like rings and fields. Group: A non-empty set G with * as operation, (G, *) is called a group if it follows the closure, associativity, identity, and inverse properties.
Group Theory Assignment 2 - Part 1. Aug 27, 2022 • 316 views. 49:46. EN Mathematics. Group Theory Assignment 2 - Part 1. Sagar Surya. 20K followers • Mathematics. Watch now Download Class PDF. Aug 27, 2022 • 49m • 316 views. In this session Sagar Surya will discuss problems on the topic of Group Theory. The class will be conducted in ...