User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts
2.4 - how to assign probability to events.
We know that probability is a number between 0 and 1. How does an event get assigned a particular probability value? Well, there are three ways of doing so:
- the personal opinion approach
- the relative frequency approach
- the classical approach
On this page, we'll take a look at each approach.
The Personal Opinion Approach Section
This approach is the simplest in practice, but therefore it also the least reliable. You might think of it as the "whatever it is to you" approach. Here are some examples:
- "I think there is an 80% chance of rain today."
- "I think there is a 50% chance that the world's oil reserves will be depleted by the year 2100."
- "I think there is a 1% chance that the men's basketball team will end up in the Final Four sometime this decade."
Example 2-4 Section
At which end of the probability scale would you put the probability that:
- one day you will die?
- you can swim around the world in 30 hours?
- you will win the lottery someday?
- a randomly selected student will get an A in this course?
- you will get an A in this course?
The Relative Frequency Approach Section
The relative frequency approach involves taking the follow three steps in order to determine P ( A ), the probability of an event A :
- Perform an experiment a large number of times, n , say.
- Count the number of times the event A of interest occurs, call the number N ( A ), say.
- Then, the probability of event A equals:
\(P(A)=\dfrac{N(A)}{n}\)
The relative frequency approach is useful when the classical approach that is described next can't be used.
Example 2-5 Section
When you toss a fair coin with one side designated as a "head" and the other side designated as a "tail", what is the probability of getting a head?
I think you all might instinctively reply \(\dfrac{1}{2}\). Of course, right? Well, there are three people who once felt compelled to determine the probability of getting a head using the relative frequency approach:
|
| , the number of heads tossed | ||
| Count Buffon | 4,040 | 2,048 | 0.5069 |
| Karl Pearson | 24,000 | 12,012 | 0.5005 |
| John Kerrich | 10,000 | 5,067 | 0.5067 |
As you can see, the relative frequency approach yields a pretty good approximation to the 0.50 probability that we would all expect of a fair coin. Perhaps this example also illustrates the large number of times an experiment has to be conducted in order to get reliable results when using the relative frequency approach.
By the way, Count Buffon (1707-1788) was a French naturalist and mathematician who often pondered interesting probability problems. His most famous question
Suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle onto the floor. What is the probability that the needle will lie across a line between two strips?
came to be known as Buffon's needle problem. Karl Pearson (1857-1936) effectively established the field of mathematical statistics. And, once you hear John Kerrich's story, you might understand why he, of all people, carried out such a mind-numbing experiment. He was an English mathematician who was lecturing at the University of Copenhagen when World War II broke out. He was arrested by the Germans and spent the war interned in a prison camp in Denmark. To help pass the time he performed a number of probability experiments, such as this coin-tossing one.
Example 2-6 Section

Some trees in a forest were showing signs of disease. A random sample of 200 trees of various sizes was examined yielding the following results:
| Type | Disease free | Doubtful | Diseased | Total |
|---|---|---|---|---|
| Large | 35 | 18 | 15 | 68 |
| Medium | 46 | 32 | 14 | 92 |
| Small | 24 | 8 | 8 | 40 |
| Total | 105 | 58 | 37 | 200 |
What is the probability that one tree selected at random is large?
There are 68 large trees out of 200 total trees, so the relative frequency approach would tell us that the probability that a tree selected at random is large is 68/200 = 0.34.
What is the probability that one tree selected at random is diseased?
There are 37 diseased trees out of 200 total trees, so the relative frequency approach would tell us that the probability that a tree selected at random is diseased is 37/200 = 0.185.
What is the probability that one tree selected at random is both small and diseased?
There are 8 small, diseased trees out of 200 total trees, so the relative frequency approach would tell us that the probability that a tree selected at random is small and diseased is 8/200 = 0.04.
What is the probability that one tree selected at random is either small or disease-free?
There are 121 trees (35 + 46 + 24 + 8 + 8) out of 200 total trees that are either small or disease-free, so the relative frequency approach would tell us that the probability that a tree selected at random is either small or disease-free is 121/200 = 0.605.
What is the probability that one tree selected at random from the population of medium trees is doubtful of disease?
There are 92 medium trees in the sample. Of those 92 medium trees, 32 have been identified as being doubtful of disease. Therefore, the relative frequency approach would tell us that the probability that a medium tree selected at random is doubtful of disease is 32/92 = 0.348.
The Classical Approach Section
The classical approach is the method that we will investigate quite extensively in the next lesson. As long as the outcomes in the sample space are equally likely (!!!), the probability of event \(A\) is:
\(P(A)=\dfrac{N(A)}{N(\mathbf{S})}\)
where \(N(A)\) is the number of elements in the event \(A\), and \(N(\mathbf{S})\) is the number of elements in the sample space \(\mathbf{S}\). Let's take a look at an example.
Example 2-7 Section
Suppose you draw one card at random from a standard deck of 52 cards. Recall that a standard deck of cards contains 13 face values (Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, and King) in 4 different suits (Clubs, Diamonds, Hearts, and Spades) for a total of 52 cards. Assume the cards were manufactured to ensure that each outcome is equally likely with a probability of 1/52. Let \(A\) be the event that the card drawn is a 2, 3, or 7. Let \(B\) be the event that the card is a 2 of hearts (H), 3 of diamonds (D), 8 of spades (S) or king of clubs (C). That is:
- \(A= \{x: x \text{ is a }2, 3,\text{ or }7\}\)
- \(B = \{x: x\text{ is 2H, 3D, 8S, or KC}\}\)
- What is the probability that a 2, 3, or 7 is drawn?
- What is the probability that the card is a 2 of hearts, 3 of diamonds, 8 of spades or king of clubs?
- What is the probability that the card is either a 2, 3, or 7 or a 2 of hearts, 3 of diamonds, 8 of spades or king of clubs?
- What is \(P(A\cap B)\)?
- Skip to primary navigation
- Skip to main content
- Skip to primary sidebar
- Skip to footer
Idea Galaxy
Adventures in Junior High and Mathematics
9 Activities for Simple Probability You Will Love
February 18, 2017 by Rachel
When you teach simple probability, it seems like you have to strike a balance between showing students how probability works and getting them to understand the math behind it. This topic lends itself to a lot of hands-on demonstrations and activities, which can be really fun. When I look for activities I know that I need hooks, practice activities and extensions. If you are looking for more about how I break down teaching and modeling simple probability, check out this post . Let’s dive into some fun and easy ways to get students thinking about simple probability.
10 activities for practice with simple probability:
Simple Probability Mazes (Printable & Digital)
Probability Fair Online Game
M&m probability activity, diamond game, qr code game, gallery walk.
Knockout Game
Rock, Paper, Scissors
Bill nye the science guy video.
Interactive Probability Tools
Anticipatory Sets or Hooks
Sometimes I forget to have hooks for my lesson. With the time crunch that always seems pressing down on me, I go through periods where I don’t use an anticipatory set. When I get back to do them, I quickly remember why they exist in the first place and just how important they really are. Hooks get kids invested in the lesson and they activate prior knowledge. So, I’m happy to share with you some of the anticipatory sets, or hooks, I use for simple probability. The following three activities really got my students ready to learn about probability:
Simple Probability Mazes
A great way to start your class is with a maze and this set of 3 mazes won’t disappoint. They increase in complexity from one maze to the next and will give your students a lot of examples to practice simple probability. I use mazes as a daily warm-up to review what students have previously learned, so these would be perfect for the middle of your simple probability unit.

If you haven’t tried a maze you’ve gotta try this one. You’ll watch your students completing the maze and not noticing how much math work they’re doing. Give it a try!
These mazes now also includes a digital version of all 3 mazes created in Google Slides. That makes this resource great for online or distance learning, as well as in the traditional class setting.
Want to get free middle school math mazes on middle school math concepts sent right to your inbox? Sign up here & join the Maze of the Month club . Once you confirm your email, you’ll instantly get a FREE integers maze to try out today.
Can’t wait to see you there!
My students love playing games online. Also, they don’t seem to be very picky about the games. As long as it is easy to understand how to play, they will play it. This game uses a few probability concepts. When you first start you have to earn tickets by choosing the best probability on a spinner wheel. The carnival theme makes it very playful. After you earn some tickets with the wheel, you can enter the carnival and play some other games. Each game has some sort of probability concept.
I showed the students how the game worked and then let them play for a few minutes. Then, we discussed how each game was related to probability. Throughout the unit I let students go back and play this game when they finished something early. By starting off by playing this game, it built students’ background and gave us a common experience to refer back to as we talked about probability.
I had found this activity ahead of time and I was super excited to use it. Each students got a little bag of M&Ms and did an experiment to predict how many M&Ms were in their bag.

I was going to do this activity on a Tuesday, but I forgot to get the M&Ms. So, I moved it to Wednesday. Then, on Wednesday morning I realized I had forgotten to get the candy, again (oops!). I then did what all teachers do from time to time, I improvised. I went through my desk and found a bag of my 3-year old son’s Halloween candy. There was a variety of candy. I decided to have students use experimental probability to predict which candy was in a bag.
There was something like 8 purple nerds, 6 pink nerds, 2 smarties, 4 gobstoppers, and 2 purple skittles and 1 red skittles. We did this as a whole class and the everyone wrote down the experimental probability as I pulled a piece of candy out and then replaced it in the bag.
One thing I would do differently is I should have done less trials. We ended up doing 22 trials and missed the chance of turning it into a proportion. But overall, it was engaging. It illustrated for students how probability is about predicting, but not knowing exactly what will happen.
This card game one was my favorite hook for this unit. I have a set of giant playing cards . Kids love them because, well, they’re ridiculous. One of the kids asked me where I got them and I told them I got them at a really big store where everything is really big. She asked if they had Gummi bears at this store, because she would love to see that! I had to break it to her that I actually bought them from an instructional supply company and there would be no really huge Gummi bear. The disappointment was real.

For this hook, we played a probability game as a whole class. This game pits the teacher against the whole class. Students first choose a suit, either heart, diamond, club, or spade. Then, you let them choose a card. If they get a card with the suit they guessed they get a point. If they don’t match the suit, then the teacher gets a point. You repeat this 10 times.
My class got a good streak going and I was afraid they were going to win, which would kinda of ruin the point, but in the end I won 6 to 4. They were so excited the whole time and they thought they were going to beat me.
After the game I asked them to figure out why this game was unfair. I let them think about it and write it down on their whiteboard. One by one I saw them getting it and writing their response. Most of them ended up with some iteration of, “The teacher had 3 chances of winning and the students had 1 chance.” They loved competing against me, and they got really into figuring out why the game was ultimately rigged. This activity was a great way to get students hooked into the lesson.
Practice Activities for Simple Probability
I’m always looking for practice activities that match the assessment I’ll be giving students at the end of the unit. Here are a few activities that kids love and that give them a lot of practice with simple probability:
Kids love QR Codes. I’m not exactly sure why they love them so much. Maybe it’s the scanning and feeling like something magical is happening. I love them because they give students the chance to be self-checking. In my class I make sure to give students a lot of individualized and specific feedback. In addition to that feedback they need to find their own mistakes and this type of activity is perfect for that. This QR code game was a great way for my students to practice with simple probability and get immediate feedback.
To play, students need to have some type of internet enabled device like an iPad or phone and install a QR Code reader on it. This particular game has 16 questions and they have simple probability situations about rolling or choose skittles out of package. I let students play it like a game against each other. They enjoy the competition.
Have you ever done a Gallery Walk in your class before? If you haven’t, I’d encourage you to try it. They’re so engaging. There are many different ways have to have them set-up to get students moving around the room while practicing. This gallery walk was set-up in centers. Each center had a situation with simple probability, and several questions to answer about that situation. Groups of 3-4 students worked together to figure them out.

This activity provides an opportunity for students to talk about probability. In my class the kids had great math talk because they didn’t always agree. They explained to each other why they believe they were right. It took a little cajoling, but I did get them to talk and have discussions. At first all they wanted to do was answer the question and move on. I walked around the room and participated with groups and asked further questions to make sure they were talking. By the end of the activity, there was a lot of discussion and learning. It was fantastic.
Knockout Game Freebie
My kids love knockout games. A Knockout Game is a game that I started making for my classes to play together to review a couple of years ago. To play, you display a game on the screen and students choose a character. Each character reveals a question. All students answer the question on their individual record sheet, and then we go over the question as a class. Students score points and there are fun bonuses where students can lose or gain more points. (read more about Knockout Games, and check out a quick video of how to play, in this post .)

This particular knockout game is a pretty fast game because the simple probability questions are fast. There are 16 questions which serve a great way to check for understanding or review before you take a test. It’s free and available for download over in my TpT store.
Extension and Performance Tasks
There isn’t always time for extension and performance tasks due to having so much to teach in such a short amount of time. But it’s good to have them handy because they can be used for fast finishers or when you have an extra few minutes.
For example, next week we have an extra 25 minutes with our homeroom because the 8th graders have high school orientation. I love Bill Nye the science guy and we are studying probability, so we’ll watch his video during this time. You can often find time for extension activities if you’re creative, or you can always wait until after state testing is over.
This link shows how you can reinforce probability through playing rock, paper, scissors. I like to use this for fast finishers. It’s a challenge to see if anyone can figure out how to beat the odds. Usually, students like to talk about what they figured out and show the rest of the class. It’s good for students to see that probability is everywhere. Also, who doesn’t love a game of rock, paper, scissors?
I’ve loved watching Bill Nye the Science Guy since I was a kid. Now, as a teacher, I wish that there were more math episodes. So I was extra excited to find this episode about probability. It used to be hard to find a copy to show students, but now it’s super easy. I paid $1.99 for this copy of an episode from Season 2, but there are free version and clips on YouTube.

Students love these videos because they’re silly and engaging. To keep students keyed in, I’ve found it helps to make sure that you have something for the students to be looking for while they’re watching the video it. Otherwise, some of them will be daydreaming the whole time. For this video I’m going to ask the following questions:
- What is the central idea of this video?
- Explain what you should do in the “Choose a Door” problem.
- What are some examples of probability in action?
- What is a bell curve and how does it work?
- Why are there runs of heads or tails when you flip a coin?
- What did you learn from this video?
- What questions do you have about this video?
I’m excited to share this video with my students this year. In addition to learning about math, I also get to share the late 80s styles which are rad and awesome!
Interactive Probability Tool
I love this interactive probability tool because it gives you multiple probability tools and you don’t have to physically have any of them. You can find similar apps on the Ipad as well. There are spinners and a coin.
I also love that this site includes discussions to help you know how to get kids talking. Click here for the discussion page . The discussion that I linked to is about how likely things are to happen. Students get a little confused about this and you can have this discussion many times until they get it.

There’s so much to use on this site. Check it out and see if you can use something from it. If you have a lot of technology, this is a fantastic way of incorporating it that’s more that just answering questions. Students will love the interactive aspect of this tool. They get to really play around with probability.
Try one thing…
Well, this is a lot of ideas. Hopefully you have lots of thoughts on how you can adapt these ideas in your classroom. To grab a set of 3 print-and-go resources for simple probability, including the gallery walk stations and the QR code game, check out this activity bundle .
I work as an academic coach for part of the day and I challenge teachers to try one thing. Make one small change that challenges you or that you have always wanted to try. Those small changes over time with help you grow as a teacher. Let’s do this!
Thanks for reading! Until next time.

Share this:
- Click to share on Twitter (Opens in new window)
- Click to share on Facebook (Opens in new window)
- Click to share on Pinterest (Opens in new window)
- Click to email a link to a friend (Opens in new window)
Grab Our Button

Privacy Policy

Recent Posts
- 10 Ways to Help Students Get Dot Plots, Histograms & Box Plots
- 12 Mean, Median, Mode & Range Activities that Rock
- 9 Volume of Prisms Activities Your Students Will Love
- 10 Sure-fire Ways to Practice Area of Triangles & Quadrilaterals
- 10 Engaging Exponents & Expressions Activities
Visit Our Store
Privacy overview.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

7.1.1: Sample Spaces and Probability (Exercises)
- Last updated
- Save as PDF
- Page ID 135445

- Rupinder Sekhon and Roberta Bloom
- De Anza College
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
SECTION 8.1 PROBLEM SET: SAMPLE SPACES AND PROBABILITY
In problems 1 - 6, write a sample space for the given experiment.
| 1) A die is rolled. | 2) A penny and a nickel are tossed. |
| 3) A die is rolled, and a coin is tossed. | 4) Three coins are tossed. |
| 5) Two dice are rolled. | 6) A jar contains four marbles numbered 1, 2, 3, and 4. Two marbles are drawn. |
In problems 7 - 12, one card is randomly selected from a deck. Find the following probabilities.
| 7) P( an ace) | 8) P( a red card) |
| 9) P( a club) | 10) P( a face card) |
| 11) P(a jack or a spade) | 12) P(a jack and a spade) |
For problems 13 - 16: A jar contains 6 red, 7 white, and 7 blue marbles. If one marble is chosen at random, find the following probabilities.
| 13) P(red) | 14) P(white) |
| 15) P(red or blue) | 16) P(red and blue) |
For problems 17 - 22: Consider a family of three children. Find the following probabilities.
| 17) P(two boys and a girl) | 18) P(at least one boy) |
| 19) P(children of both sexes) | 20) P(at most one girl) |
| 21) P(first and third children are male) | 22) P(all children are of the same gender) |
For problems 23 - 27: Two dice are rolled. Find the following probabilities.
| 23) P(the sum of the dice is 5) | 24) P(the sum of the dice is 8) |
| 25) P(the sum is 3 or 6) | 26) P(the sum is more than 10) |
| 27) P(the result is a double) (Hint: a double means that both dice show the same value) | |
For problems 28-31: A jar contains four marbles numbered 1, 2, 3, and 4. Two marbles are drawn randomly WITHOUT REPLACEMENT. That means that after a marble is drawn it is NOT replaced in the jar before the second marble is selected. Find the following probabilities.
| 28) P(the sum of the numbers is 5) | 29) P(the sum of the numbers is odd) |
| 30) P(the sum of the numbers is 9) | 31) P(one of the numbers is 3) |
For problems 32-33: A jar contains four marbles numbered 1, 2, 3, and 4. Two marbles are drawn randomly WITH REPLACEMENT. That means that after a marble is drawn it is replaced in the jar before the second marble is selected. Find the following probabilities.
| 32) P(the sum of the numbers is 5) | 33) P(the sum of the numbers is 2) |
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 7: Probability
About this unit.
Probability tells us how often some event will happen after many repeated trials. You've experienced probability when you've flipped a coin, rolled some dice, or looked at a weather forecast. Go deeper with your understanding of probability as you learn about theoretical, experimental, and compound probability, and investigate permutations, combinations, and more!
Basic theoretical probability
- Intro to theoretical probability (Opens a modal)
- Probability: the basics (Opens a modal)
- Simple probability: yellow marble (Opens a modal)
- Simple probability: non-blue marble (Opens a modal)
- Intuitive sense of probabilities (Opens a modal)
- The Monty Hall problem (Opens a modal)
- Simple probability Get 5 of 7 questions to level up!
- Comparing probabilities Get 5 of 7 questions to level up!
Probability using sample spaces
- Example: All the ways you can flip a coin (Opens a modal)
- Die rolling probability (Opens a modal)
- Subsets of sample spaces (Opens a modal)
- Subsets of sample spaces Get 3 of 4 questions to level up!
Basic set operations
- Intersection and union of sets (Opens a modal)
- Relative complement or difference between sets (Opens a modal)
- Universal set and absolute complement (Opens a modal)
- Subset, strict subset, and superset (Opens a modal)
- Bringing the set operations together (Opens a modal)
- Basic set notation Get 5 of 7 questions to level up!
Experimental probability
- Experimental probability (Opens a modal)
- Theoretical and experimental probabilities (Opens a modal)
- Making predictions with probability (Opens a modal)
- Simulation and randomness: Random digit tables (Opens a modal)
- Experimental probability Get 5 of 7 questions to level up!
- Making predictions with probability Get 5 of 7 questions to level up!
Randomness, probability, and simulation
- Experimental versus theoretical probability simulation (Opens a modal)
- Theoretical and experimental probability: Coin flips and die rolls (Opens a modal)
- Random number list to run experiment (Opens a modal)
- Random numbers for experimental probability (Opens a modal)
- Statistical significance of experiment (Opens a modal)
- Interpret results of simulations Get 3 of 4 questions to level up!
Addition rule
- Probability with Venn diagrams (Opens a modal)
- Addition rule for probability (Opens a modal)
- Addition rule for probability (basic) (Opens a modal)
- Adding probabilities Get 3 of 4 questions to level up!
- Two-way tables, Venn diagrams, and probability Get 3 of 4 questions to level up!
Multiplication rule for independent events
- Sample spaces for compound events (Opens a modal)
- Compound probability of independent events (Opens a modal)
- Probability of a compound event (Opens a modal)
- "At least one" probability with coin flipping (Opens a modal)
- Free-throw probability (Opens a modal)
- Three-pointer vs free-throw probability (Opens a modal)
- Probability without equally likely events (Opens a modal)
- Independent events example: test taking (Opens a modal)
- Die rolling probability with independent events (Opens a modal)
- Probabilities involving "at least one" success (Opens a modal)
- Sample spaces for compound events Get 3 of 4 questions to level up!
- Independent probability Get 3 of 4 questions to level up!
- Probabilities of compound events Get 3 of 4 questions to level up!
- Probability of "at least one" success Get 3 of 4 questions to level up!
Multiplication rule for dependent events
- Dependent probability introduction (Opens a modal)
- Dependent probability: coins (Opens a modal)
- Dependent probability example (Opens a modal)
- Independent & dependent probability (Opens a modal)
- The general multiplication rule (Opens a modal)
- Dependent probability (Opens a modal)
- Dependent probability Get 3 of 4 questions to level up!
Conditional probability and independence
- Calculating conditional probability (Opens a modal)
- Conditional probability explained visually (Opens a modal)
- Conditional probability using two-way tables (Opens a modal)
- Conditional probability tree diagram example (Opens a modal)
- Tree diagrams and conditional probability (Opens a modal)
- Conditional probability and independence (Opens a modal)
- Analyzing event probability for independence (Opens a modal)
- Calculate conditional probability Get 3 of 4 questions to level up!
- Dependent and independent events Get 3 of 4 questions to level up!
Probability of Simple Events
Practice finding the probability of simple events with this one-page worksheet! Geared toward seventh-grade learners, this worksheet gives students hands-on practice calculating simple probabilities in the context of real-world scenarios. Learners are presented with six relatable problems about movies, restaurants, dogs, and more, and they will need to determine the probability of certain outcomes in each scenario. Being able to determine the probability of simple events is an important skill in daily life, as well as in more complex math topics. For an introduction to probability or as a helpful warm-up activity, check out the What’s the Probability? worksheet!
View aligned standards

Child Login
- Kindergarten
- Number charts
- Skip Counting
- Place Value
- Number Lines
- Subtraction
- Multiplication
- Word Problems
- Comparing Numbers
- Ordering Numbers
- Odd and Even
- Prime and Composite
- Roman Numerals
- Ordinal Numbers
- In and Out Boxes
- Number System Conversions
- More Number Sense Worksheets
- Size Comparison
- Measuring Length
- Metric Unit Conversion
- Customary Unit Conversion
- Temperature
- More Measurement Worksheets
- Writing Checks
- Profit and Loss
- Simple Interest
- Compound Interest
- Tally Marks
- Mean, Median, Mode, Range
- Mean Absolute Deviation
- Stem-and-leaf Plot
- Box-and-whisker Plot
- Permutation and Combination
- Probability
- Venn Diagram
- More Statistics Worksheets
- Shapes - 2D
- Shapes - 3D
- Lines, Rays and Line Segments
- Points, Lines and Planes
- Transformation
- Quadrilateral
- Ordered Pairs
- Midpoint Formula
- Distance Formula
- Parallel, Perpendicular and Intersecting Lines
- Scale Factor
- Surface Area
- Pythagorean Theorem
- More Geometry Worksheets
- Converting between Fractions and Decimals
- Significant Figures
- Convert between Fractions, Decimals, and Percents
- Proportions
- Direct and Inverse Variation
- Order of Operations
- Squaring Numbers
- Square Roots
- Scientific Notations
- Speed, Distance, and Time
- Absolute Value
- More Pre-Algebra Worksheets
- Translating Algebraic Phrases
- Evaluating Algebraic Expressions
- Simplifying Algebraic Expressions
- Algebraic Identities
- Quadratic Equations
- Systems of Equations
- Polynomials
- Inequalities
- Sequence and Series
- Complex Numbers
- More Algebra Worksheets
- Trigonometry
- Math Workbooks
- English Language Arts
- Summer Review Packets
- Social Studies
- Holidays and Events
- Worksheets >
- Statistics >
Probability Worksheets
Navigate through this assortment of printable probability worksheets that includes exercises on basic probability based on more likely, less likely, equally likely, certain and impossible events, pdf worksheets based on identifying suitable events, simple spinner problems, for students in grade 4, grade 5, and grade 6. With the required introduction, the beginners get to further their knowledge with skills like probability on single coin, two coins, days in a week, months in a year, fair die, pair of dice, deck of cards, numbers and more. Mutually exclusive and inclusive events, probability on odds and other challenging probability worksheets are useful for grade 7, grade 8, and high school. Grab some of these probability worksheets for free!
Probability on Coins
Simple probability worksheets based on tossing single coin or two coins. Identify the proper sample space before finding probability.
Probability in a single coin toss
Probability in pair of coin - 1
Probability in pair of coin - 2
Probability on Days and Months
Fun filled worksheet pdfs based on days in a week and months in a year. Sample space is easy to find but care is required in identifying like events.
Days of a week
Months of a year - 1
Months of a year - 2
Probability on Fair Die
Fair die is numbered from 1 to 6. Understand the multiples, divisors and factors and apply it on these probability worksheets.
Simple numbers
Multiples and divisors
Mutually exclusive and inclusive
Probability on Pair of Dice
Sample space is little large which contains 36 elements. Write all of them in papers before start answering on probability questions for grade 7 and grade 8.
Based on numbers
Based on sum and difference
Based on multiples and divisors
Based on factors
Probability on Numbers
Students should learn the concepts of multiples, divisors and factors before start practicing these printable worksheets.
Probability on numbers - 1
Probability on numbers - 2
Probability on numbers - 3
Probability on numbers - 4
Probability on numbers - 5
Probability on Deck of Cards
Deck of cards contain 52 cards, 26 are black, 26 are red, four different flowers, each flower contain 13 cards such as A, 1, 2, ..., 10, J, Q, K.
Deck of cards worksheet - 1
Deck of cards worksheet - 2
Deck of cards worksheet - 3
Probability on Spinners
Interactive worksheets for 4th grade and 5th grade kids to understand the probability using spinners. Colorful spinners are included for more fun.
Spinner worksheets on numbers
Spinner worksheets on colors
Probability on Odds
Probability on odds worksheets can be broadly classifieds as favorable to the events or against the events.
Odds worksheet - 1
Odds worksheet - 2
Odds worksheet - 3
Probability on Independent and Dependent
Here comes our challenging probability worksheets set for 8th grade and high school students based on dependent and independent events with various real-life applications.
Based on deck of cards
Based on marbles
Based on cards
Probability on Different Events
Basic probability worksheets for beginners in 6th grade and 7th grade to understand the different type of events such as more likely, less likely, equally likely and so on.
Balls in container
Identify suitable events
Mutually inclusive and exclusive events
Related Worksheets
» Permutation
» Combination
» Permutation and Combination
» Venn Diagram
Become a Member
Membership Information
Privacy Policy
What's New?
Printing Help
Testimonial
Copyright © 2024 - Math Worksheets 4 Kids
This is a members-only feature!

- Math Article
Probability

Probability means possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one. Probability has been introduced in Maths to predict how likely events are to happen. The meaning of probability is basically the extent to which something is likely to happen. This is the basic probability theory, which is also used in the probability distribution , where you will learn the possibility of outcomes for a random experiment. To find the probability of a single event to occur, first, we should know the total number of possible outcomes.
Learn More here: Study Mathematics
Probability Definition in Math
Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty. We can predict only the chance of an event to occur i.e., how likely they are going to happen, using it. Probability can range from 0 to 1, where 0 means the event to be an impossible one and 1 indicates a certain event. Probability for Class 10 is an important topic for the students which explains all the basic concepts of this topic. The probability of all the events in a sample space adds up to 1.
For example , when we toss a coin, either we get Head OR Tail, only two possible outcomes are possible (H, T). But when two coins are tossed then there will be four possible outcomes, i.e {(H, H), (H, T), (T, H), (T, T)}.
Download this lesson as PDF: – Download PDF Here
Formula for Probability
The probability formula is defined as the possibility of an event to happen is equal to the ratio of the number of favourable outcomes and the total number of outcomes.
Sometimes students get mistaken for “favourable outcome” with “desirable outcome”. This is the basic formula. But there are some more formulas for different situations or events.
Solved Examples
1) There are 6 pillows in a bed, 3 are red, 2 are yellow and 1 is blue. What is the probability of picking a yellow pillow?
Ans: The probability is equal to the number of yellow pillows in the bed divided by the total number of pillows, i.e. 2/6 = 1/3.
2) There is a container full of coloured bottles, red, blue, green and orange. Some of the bottles are picked out and displaced. Sumit did this 1000 times and got the following results:
- No. of blue bottles picked out: 300
- No. of red bottles: 200
- No. of green bottles: 450
- No. of orange bottles: 50
a) What is the probability that Sumit will pick a green bottle?
Ans: For every 1000 bottles picked out, 450 are green.
Therefore, P(green) = 450/1000 = 0.45
b) If there are 100 bottles in the container, how many of them are likely to be green?
Ans: The experiment implies that 450 out of 1000 bottles are green.
Therefore, out of 100 bottles, 45 are green.
Probability Tree
The tree diagram helps to organize and visualize the different possible outcomes. Branches and ends of the tree are two main positions. Probability of each branch is written on the branch, whereas the ends are containing the final outcome. Tree diagrams are used to figure out when to multiply and when to add. You can see below a tree diagram for the coin:

Types of Probability
There are three major types of probabilities:
Theoretical Probability
Experimental probability, axiomatic probability.
It is based on the possible chances of something to happen. The theoretical probability is mainly based on the reasoning behind probability. For example, if a coin is tossed, the theoretical probability of getting a head will be ½.
It is based on the basis of the observations of an experiment. The experimental probability can be calculated based on the number of possible outcomes by the total number of trials. For example, if a coin is tossed 10 times and head is recorded 6 times then, the experimental probability for heads is 6/10 or, 3/5.
In axiomatic probability, a set of rules or axioms are set which applies to all types. These axioms are set by Kolmogorov and are known as Kolmogorov’s three axioms. With the axiomatic approach to probability, the chances of occurrence or non-occurrence of the events can be quantified. The axiomatic probability lesson covers this concept in detail with Kolmogorov’s three rules (axioms) along with various examples.
Conditional Probability is the likelihood of an event or outcome occurring based on the occurrence of a previous event or outcome.
Probability of an Event
Assume an event E can occur in r ways out of a sum of n probable or possible equally likely ways . Then the probability of happening of the event or its success is expressed as;
The probability that the event will not occur or known as its failure is expressed as:
P(E’) = (n-r)/n = 1-(r/n)
E’ represents that the event will not occur.
Therefore, now we can say;
P(E) + P(E’) = 1
This means that the total of all the probabilities in any random test or experiment is equal to 1.
What are Equally Likely Events?
When the events have the same theoretical probability of happening, then they are called equally likely events. The results of a sample space are called equally likely if all of them have the same probability of occurring. For example, if you throw a die, then the probability of getting 1 is 1/6. Similarly, the probability of getting all the numbers from 2,3,4,5 and 6, one at a time is 1/6. Hence, the following are some examples of equally likely events when throwing a die:
- Getting 3 and 5 on throwing a die
- Getting an even number and an odd number on a die
- Getting 1, 2 or 3 on rolling a die
are equally likely events, since the probabilities of each event are equal.
Complementary Events
The possibility that there will be only two outcomes which states that an event will occur or not. Like a person will come or not come to your house, getting a job or not getting a job, etc. are examples of complementary events. Basically, the complement of an event occurring in the exact opposite that the probability of it is not occurring. Some more examples are:
- It will rain or not rain today
- The student will pass the exam or not pass.
- You win the lottery or you don’t.
Also, read:
- Independent Events
- Mutually Exclusive Events
Probability Theory
Probability theory had its root in the 16th century when J. Cardan, an Italian mathematician and physician, addressed the first work on the topic, The Book on Games of Chance. After its inception, the knowledge of probability has brought to the attention of great mathematicians. Thus, Probability theory is the branch of mathematics that deals with the possibility of the happening of events. Although there are many distinct probability interpretations, probability theory interprets the concept precisely by expressing it through a set of axioms or hypotheses. These hypotheses help form the probability in terms of a possibility space, which allows a measure holding values between 0 and 1. This is known as the probability measure, to a set of possible outcomes of the sample space.
Probability Density Function
The Probability Density Function (PDF) is the probability function which is represented for the density of a continuous random variable lying between a certain range of values. Probability Density Function explains the normal distribution and how mean and deviation exists. The standard normal distribution is used to create a database or statistics, which are often used in science to represent the real-valued variables, whose distribution is not known.
Probability Terms and Definition
Some of the important probability terms are discussed here:
| Term | Definition | Example |
|---|---|---|
| Sample Space | The set of all the possible outcomes to occur in any trial | |
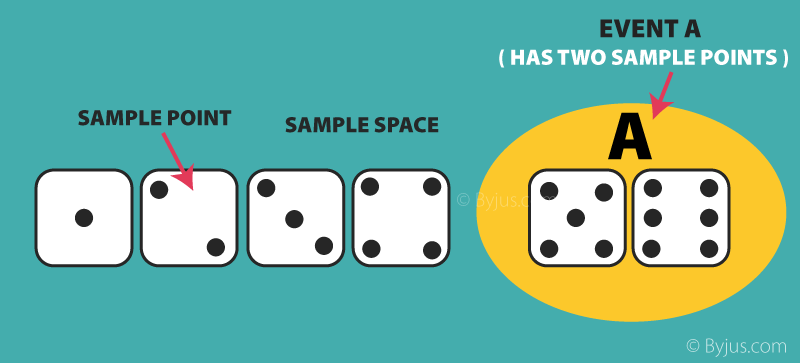
| Sample Point | It is one of the possible results | In a deck of Cards: |
| Experiment or Trial | A series of actions where the outcomes are always uncertain. | The tossing of a coin, Selecting a card from a deck of cards, throwing a dice. |
| Event | It is a single outcome of an experiment. | Getting a Heads while tossing a coin is an event. |
| Outcome | Possible result of a trial/experiment | T (tail) is a possible outcome when a coin is tossed. |
| Complimentary event | The non-happening events. The complement of an event A is the event, not A (or A’) | In a standard 52-card deck, A = Draw a heart, then A’ = Don’t draw a heart |
| Impossible Event | The event cannot happen | In tossing a coin, impossible to get both head and tail at the same time |
Applications of Probability
Probability has a wide variety of applications in real life. Some of the common applications which we see in our everyday life while checking the results of the following events:
- Choosing a card from the deck of cards
- Flipping a coin
- Throwing a dice in the air
- Pulling a red ball out of a bucket of red and white balls
- Winning a lucky draw
Other Major Applications of Probability
- It is used for risk assessment and modelling in various industries
- Weather forecasting or prediction of weather changes
- Probability of a team winning in a sport based on players and strength of team
- In the share market, chances of getting the hike of share prices
Problems and Solutions on Probability
Question 1: Find the probability of ‘getting 3 on rolling a die’.
Sample Space = S = {1, 2, 3, 4, 5, 6}
Total number of outcomes = n(S) = 6
Let A be the event of getting 3.
Number of favourable outcomes = n(A) = 1
i.e. A = {3}
Probability, P(A) = n(A)/n(S) = 1/6
Hence, P(getting 3 on rolling a die) = 1/6
Question 2: Draw a random card from a pack of cards. What is the probability that the card drawn is a face card?
A standard deck has 52 cards.
Total number of outcomes = n(S) = 52
Let E be the event of drawing a face card.
Number of favourable events = n(E) = 4 x 3 = 12 (considered Jack, Queen and King only)
Probability, P = Number of Favourable Outcomes/Total Number of Outcomes
P(E) = n(E)/n(S)
P(the card drawn is a face card) = 3/13
Question 3: A vessel contains 4 blue balls, 5 red balls and 11 white balls. If three balls are drawn from the vessel at random, what is the probability that the first ball is red, the second ball is blue, and the third ball is white?
The probability to get the first ball is red or the first event is 5/20.
Since we have drawn a ball for the first event to occur, then the number of possibilities left for the second event to occur is 20 – 1 = 19.
Hence, the probability of getting the second ball as blue or the second event is 4/19.
Again with the first and second event occurring, the number of possibilities left for the third event to occur is 19 – 1 = 18.
And the probability of the third ball is white or the third event is 11/18.
Therefore, the probability is 5/20 x 4/19 x 11/18 = 44/1368 = 0.032.
Or we can express it as: P = 3.2%.
Question 4: Two dice are rolled, find the probability that the sum is:
- less than 13
Video Lectures
Introduction.

Solving Probability Questions

Probability Important Topics


Probability Important Questions

Probability Problems
- Two dice are thrown together. Find the probability that the product of the numbers on the top of the dice is: (i) 6 (ii) 12 (iii) 7
- A bag contains 10 red, 5 blue and 7 green balls. A ball is drawn at random. Find the probability of this ball being a (i) red ball (ii) green ball (iii) not a blue ball
- All the jacks, queens and kings are removed from a deck of 52 playing cards. The remaining cards are well shuffled and then one card is drawn at random. Giving ace a value 1 similar value for other cards, find the probability that the card has a value (i) 7 (ii) greater than 7 (iii) less than 7
- A die has its six faces marked 0, 1, 1, 1, 6, 6. Two such dice are thrown together and the total score is recorded. (i) How many different scores are possible? (ii) What is the probability of getting a total of 7?
Frequently Asked Questions (FAQs) on Probability
What is probability give an example, what is the formula of probability, what are the different types of probability, what are the basic rules of probability, what is the complement rule in probability.
In probability, the complement rule states that “the sum of probabilities of an event and its complement should be equal to 1”. If A is an event, then the complement rule is given as: P(A) + P(A’) = 1.
What are the different ways to present the probability value?
The three ways to present the probability values are:
- Decimal or fraction
What does the probability of 0 represent?
The probability of 0 represents that the event will not happen or that it is an impossible event.
What is the sample space for tossing two coins?
The sample space for tossing two coins is: S = {HH, HT, TH, TT}

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below
Request OTP on Voice Call
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Post My Comment
good basics concepts provide
Great video content. Perfectly explained for examinations. I really like to learn from BYJU’s
Thank you for your best information on probablity
Good explanation about probability and concept for simple understanding the overall chapter. I hope this is a good way to understand the CONCEPT
For learner of class X standard , it is providing all the relevant informations and approach towards the contenet is knitted in an elegant manner and students will have the opportunity to grasp the topic easily and will be immensely benefited.
this topic has been hard for me but now I know what it is all about and I have really enjoyed it thanks for your good explanation
Well explained
Excellent explanation of probability. One can easily understand about the probability.
I really appreciated your explanations because it’s well understandable Thanks
Love the way you teach
There are 3 boxes Box A contains 10 bulbs out of which 4 are dead box b contains 6 bulbs out of which 1 is dead box c contains 8 bulbs out of which 3 are dead. If a dead bulb is picked at random find the probability that it is from which box?
Probability of selecting a dead bulb from the first box = (1/3) x (4/10) = 4/30 Probability of selecting a dead bulb from the second box = (1/3) x (1/6) = 1/18 Probability of selecting a dead bulb from the third box = (1/3) x (3/8) = 3/24 = 1/8 Total probability = (4/30) + (1/18) + (1/8) = (48 + 20 + 45)360 =113/360
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Probability Questions with Solutions
Tutorial on finding the probability of an event. In what follows, S is the sample space of the experiment in question and E is the event of interest. n(S) is the number of elements in the sample space S and n(E) is the number of elements in the event E.
Questions and their Solutions
| color | frequency |
|---|---|
| red | 3 |
| green | 7 |
| white | 10 |
| group | frequency |
|---|---|
| a | 50 |
| B | 65 |
| O | 70 |
| AB | 15 |
Answers to the above exercises
More references and links.
- Pre-Algebra Topics
- Algebra Topics
- Algebra Calculator
- Algebra Cheat Sheet
- Algebra Practice Test
- Algebra Readiness Test
- Algebra Formulas
- Want to Build Your Own Website?
Sign In / Register
Use These Examples of Probability To Guide You Through Calculating the Probability of Simple Events
Probability is the chance or likelihood that an event will happen.
It is the ratio of the number of ways an event can occur to the number of possible outcomes. We'll use the following model to help calculate the probability of simple events.
As you can see, with this formula, we will write the probability of an event as a fraction.
The numerator (in red) is the number of chances and the denominator (in blue) is the set of all possible outcomes. This is also known as the sample space.
Let's take a look at a few examples of probability.
Example 1- Probability Using a Die
Given a standard die, determine the probability for the following events when rolling the die one time:
P(even number)
Before we start the solution, please take note that:
P(5) means the probability of rolling a 5
When you see P( ) this means to find the probability of whatever is indicated inside of the parenthesis.
Solutions :
Let’s first identify the sample space. The sample space then becomes the denominator in our fraction when calculating probability.
Sample Space : 6 We are using a standard die. A standard die has 6 sides and contains the numbers 1-6.
Therefore, our sample space is 6 because there are 6 total outcomes that could occur when we roll the die. The 6 outcomes are: 1, 2, 3, 4, 5, 6

Special Note:
Always simplify your fraction if possible!

Now let's take a look at a probability situation that involves marbles.
Example 2 - Probability with Marbles
There are 4 blue marbles, 5 red marbles, 1 green marble, and 2 black marbles in a bag. Suppose you select one marble at random. Find each probability.

P(blue or black)
P(not green)
P(not purple)

Hopefully these two examples have helped you to apply the formula in order to calculate the probability for any simple event.
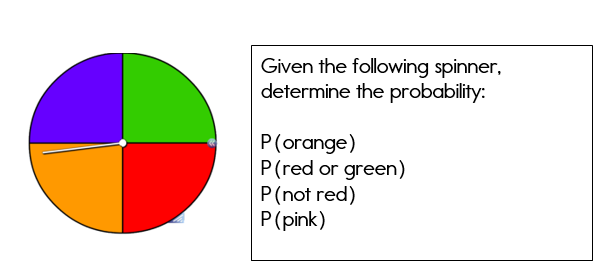
Now, it's your turn to try! Check out the spinner in the practice problem below.
Practice Problem
Great Job! You've got the basics, now you are ready to move on to the next lesson on Tree Diagrams & The Fundamental Counting Principle.
- Probability
- Simple Probability

Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
ALGEBRA CLASS E-COURSE MEMBERS

Click here for more information on our Algebra Class e-courses.

Need Help? Try This Online Calculator!
Affiliate Products...
On this site, I recommend only one product that I use and love and that is Mathway If you make a purchase on this site, I may receive a small commission at no cost to you.
Privacy Policy
Let Us Know How we are doing!
send us a message to give us more detail!
| Facebook X |
Would you prefer to share this page with others by linking to it?
- Click on the HTML link code below.
- Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.
Copyright © 2009-2020 | Karin Hutchinson | ALL RIGHTS RESERVED.
- STEM Ambassadors
- School trusts
- ITE and governors
- Invest in schools
- STEM careers inspiration
- Benefits and impact
- Our supporters
- Become a STEM Ambassador
- Request a STEM Ambassador
- Employer information
- Training and support
- STEM Ambassadors Partners
- Working with community groups
- Search icon
- Join the STEM Community
Simple Probability Experiments
The topic area of probability provides a good opportunity for students to engage in practical work as a means of gaining an understanding of the basic principles of probability. This resource package contains a variety of activities providing opportunity for students to record and describe the outcomes of simple probability experiments involving randomness, fairness, equally and unequally likely outcomes using appropriate language and use and understand the 0-1 scale.
Visit the secondary mathematics webpage to access all lists.
Handling Data 2
Quality Assured Category: Mathematics Publisher: Nuffield Foundation
This resource has nine handling data units. Unit 3 is the section of work appropriate to this topic. In Understanding and using the probability scale students are presented with a number of different situations in which they have to use a number line and appropriate vocabulary. In Probability using different numbers, students use fractions, decimals and percentages to represent probabilities. Making conjectures and analysing results requires students to use the results of experiments to make predictions.

Probability
Quality Assured Category: Mathematics Publisher: SMILE
This resource contains investigations, worksheets and practical activities. The activities appropriate to this topic in probability pack one are:
Likely or unlikely in which students are asked to categorise probability statements.
Experiments where students throw a dice sixty times and record the results.
Strange dice game in which students have to decide whether or not the game is fair.
Lucky dip in which students attempt to decribe the results from an experiment.
Fair play in which students determine whether a game is fair.
How likely which contains experiments with spinners and a probability scale.

Quality Assured Category: Mathematics Publisher: Centre for Innovation in Mathematics Teaching
In Probability students explore the use of the probability scale by considering a number of examples which are useful when introducing probability. The activity file describes a dice game in which students have to experiment to determine the probability of wining. The second activity explores a Russian fable which tells of an experiment to determine who is to be married next. The third experiment investigates the likelihood that people will have the same birthdate.

Good ideas for Probability
Quality Assured Category: Mathematics Publisher: Polygon Resources
These activities encourage students to develop their own games with appropriate time to work on them and test out their hypotheses.
Horse Race asks students to investigate whether this is a fair game.
Crossing the River involves students playing a game and then modifying it to determine whether it is now easier or harder to win and why.
21 Dice asks students to experiment with differently numbered dice to find the highest totals possible when the die is thrown and the numbers are added together.
Bingo e ncourages students to invent their own variation of the game by experimenting with other types and numbers of dice with appropriate bingo cards.
Snap involves students using a subset of cards from a full pack to play a game of snap, record their results then investigate what happens with different subsets.
Pinball Machine is an experiment to determine whether or not a particular pinball machine would produce a profit.
Roll a Penny is an experiment with grids of different sizes and the probability of achieving a desirable outcome.
Students can be placed in groups, each group investigating a diffrent game. Groups can present their findings to the rest of the class.

Probability Mystery
Quality Assured Category: Mathematics Publisher: Durham County Council
This resource has fourteen cards with statements about the likelihood of six different runners winning a race. Students are tasked with using the statements on the cards to determine who is most likely to win the race, with what probability, and in what sequence they would expect the runners to finish.
The mathematics that students need to complete the challenge is knowledge of the probability scale, to understand the probability of certainty; ‘evens chance’, likelihood and chance.

Ordering Probabilities S1
Quality Assured Category: Mathematics Publisher: Department for Education
In this resource students learn to understand that probabilities are assigned values between 0 and 1. Students decide an appropriate value for the probability of a given event and use some of the vocabulary associated with probability such as ‘certain’, ‘impossible’, ‘likely’. They will develop their ability to order decimals between 0 and 1. Students should have some experience of decimal numbers.

Evaluating Probability Statements S2
In this resource students discuss and clarify some common misconceptions about probability. This involves discussing the concepts of equally likely events, randomness and sample sizes. Students also learn to reason and explain. This session assumes that learners have encountered probability before. It aims to draw on their prior knowledge and develop it through discussion; it does not assume that they are already competent.
Quality Assured Category: Mathematics Publisher: The Virtual Textbook
This resource contains four interactive excel files dealing with:
Probability Line and Simple Examples This excel file begins with the probability number line labelled with fractions, decimals and percentages. The next two interactive sheets pose problems about selecting a coloured ball from a bag with answers shown as a fraction, simplified fraction and percentage. Other sheets pose questions about selecting a letters from a given word and rolling a single die. The final interactive sheet shows the possibility space when two dice are thrown and the answers to the questions posed are shown as fractions and simplified fractions.
There are a further five sheets of questions which may be suitable for use in the classroom.
Probability: Biased Coins This short interactive program illustrates the effect of bias when a number of coins are tossed. The first sheet deals with the experiment when 10 coins are tossed when the probability of getting a head can be altered. The probability of getting a particular number of heads is shown in a table (alongside the cumulative probability) and in a bar chart. The second interactive sheet deals with a similar experiment when 20 coins are tossed.
There are three more sheets of questions which may be suitable for use in the classroom.
Probability: Relative Frequency This excel file simulates selecting an object from a given number of objects in a bag. The outcomes are shown in a tally chart and the problem is to predict how many of each coloured object there are in the bag. The contents of the bag can be revealed on a separate sheet.
Probability: Two Events This interactive file starts gently with a sheet showing the 52 cards in a standard deck. Questions are posed about the probability of selecting a single card and answers can be revealed. The next two sheets deal with probabilities associated with selecting two cards, one with replacement and the other without replacement. The outcomes are shown on tree diagrams and the probabilities on each branch can be revealed. The problem of rolling two dice is similarly dealt with on the next two sheets with one of them using biased dice. The final interactive sheet uses a tree diagram to illustrate the solution to problems related to selection of objects from two different bags.
There are a further eight sheets of questions which may be suitable for use in the classroom.


- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

3.1: Sample Spaces, Events, and Their Probabilities
- Last updated
- Save as PDF
- Page ID 530

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Learning Objectives
- To learn the concept of the sample space associated with a random experiment.
- To learn the concept of an event associated with a random experiment.
- To learn the concept of the probability of an event.
Sample Spaces and Events
Rolling an ordinary six-sided die is a familiar example of a random experiment , an action for which all possible outcomes can be listed, but for which the actual outcome on any given trial of the experiment cannot be predicted with certainty. In such a situation we wish to assign to each outcome, such as rolling a two, a number, called the probability of the outcome, that indicates how likely it is that the outcome will occur. Similarly, we would like to assign a probability to any event , or collection of outcomes, such as rolling an even number, which indicates how likely it is that the event will occur if the experiment is performed. This section provides a framework for discussing probability problems, using the terms just mentioned.
Definition: random experiment
A random experiment is a mechanism that produces a definite outcome that cannot be predicted with certainty. The sample space associated with a random experiment is the set of all possible outcomes. An event is a subset of the sample space.
Definition: Element and Occurrence
An event \(E\) is said to occur on a particular trial of the experiment if the outcome observed is an element of the set \(E\).
Example \(\PageIndex{1}\): Sample Space for a single coin
Construct a sample space for the experiment that consists of tossing a single coin.
The outcomes could be labeled \(h\) for heads and \(t\) for tails. Then the sample space is the set: \(S = \{h,t\}\)
Example \(\PageIndex{2}\): Sample Space for a single die
Construct a sample space for the experiment that consists of rolling a single die. Find the events that correspond to the phrases “an even number is rolled” and “a number greater than two is rolled.”
The outcomes could be labeled according to the number of dots on the top face of the die. Then the sample space is the set \(S = \{1,2,3,4,5,6\}\)
The outcomes that are even are \(2, 4,\; \; \text{and}\; \; 6\), so the event that corresponds to the phrase “an even number is rolled” is the set \(\{2,4,6\}\), which it is natural to denote by the letter \(E\). We write \(E=\{2,4,6\}\).
Similarly the event that corresponds to the phrase “a number greater than two is rolled” is the set \(T=\{3,4,5,6\}\), which we have denoted \(T\).
A graphical representation of a sample space and events is a Venn diagram , as shown in Figure \(\PageIndex{1}\). In general the sample space \(S\) is represented by a rectangle, outcomes by points within the rectangle, and events by ovals that enclose the outcomes that compose them.

Example \(\PageIndex{3}\): Sample Spaces for two coines
A random experiment consists of tossing two coins.
- Construct a sample space for the situation that the coins are indistinguishable, such as two brand new pennies.
- Construct a sample space for the situation that the coins are distinguishable, such as one a penny and the other a nickel.
- After the coins are tossed one sees either two heads, which could be labeled \(2h\), two tails, which could be labeled \(2t\), or coins that differ, which could be labeled \(d\) Thus a sample space is \(S=\{2h, 2t, d\}\).
- Since we can tell the coins apart, there are now two ways for the coins to differ: the penny heads and the nickel tails, or the penny tails and the nickel heads. We can label each outcome as a pair of letters, the first of which indicates how the penny landed and the second of which indicates how the nickel landed. A sample space is then \(S' = \{hh, ht, th, tt\}\).
A device that can be helpful in identifying all possible outcomes of a random experiment, particularly one that can be viewed as proceeding in stages, is what is called a tree diagram . It is described in the following example.
Example \(\PageIndex{4}\): Tree diagram
Construct a sample space that describes all three-child families according to the genders of the children with respect to birth order.
Two of the outcomes are “two boys then a girl,” which we might denote \(bbg\), and “a girl then two boys,” which we would denote \(gbb\).
Clearly there are many outcomes, and when we try to list all of them it could be difficult to be sure that we have found them all unless we proceed systematically. The tree diagram shown in Figure \(\PageIndex{2}\), gives a systematic approach.
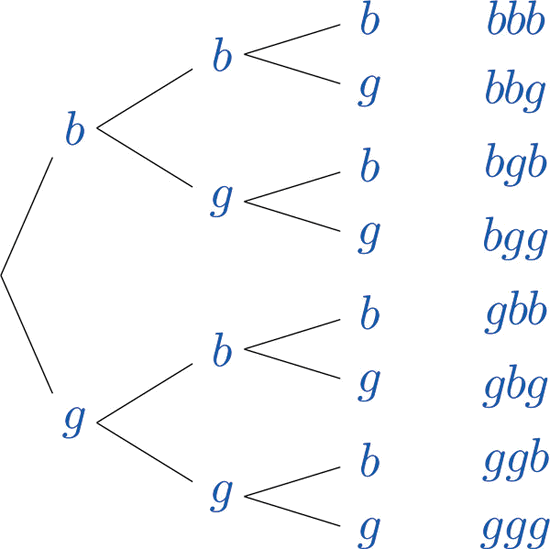
The diagram was constructed as follows. There are two possibilities for the first child, boy or girl, so we draw two line segments coming out of a starting point, one ending in a \(b\) for “boy” and the other ending in a \(g\) for “girl.” For each of these two possibilities for the first child there are two possibilities for the second child, “boy” or “girl,” so from each of the \(b\) and \(g\) we draw two line segments, one segment ending in a \(b\) and one in a \(g\). For each of the four ending points now in the diagram there are two possibilities for the third child, so we repeat the process once more.
The line segments are called branches of the tree. The right ending point of each branch is called a node . The nodes on the extreme right are the final nodes ; to each one there corresponds an outcome, as shown in the figure.
From the tree it is easy to read off the eight outcomes of the experiment, so the sample space is, reading from the top to the bottom of the final nodes in the tree,
\[S=\{bbb,\; bbg,\; bgb,\; bgg,\; gbb,\; gbg,\; ggb,\; ggg\} \nonumber \]
Probability
Definition: probability.
The probability of an outcome \(e\) in a sample space \(S\) is a number \(P\) between \(1\) and \(0\) that measures the likelihood that \(e\) will occur on a single trial of the corresponding random experiment. The value \(P=0\) corresponds to the outcome \(e\) being impossible and the value \(P=1\) corresponds to the outcome \(e\) being certain.
Definition: probability of an event
The probability of an event \(A\) is the sum of the probabilities of the individual outcomes of which it is composed. It is denoted \(P(A)\).
The following formula expresses the content of the definition of the probability of an event:
If an event \(E\) is \(E=\{e_1,e_2,...,e_k\}\), then
\[P(E)=P(e_1)+P(e_2)+...+P(e_k) \nonumber \]
The following figure expresses the content of the definition of the probability of an event:
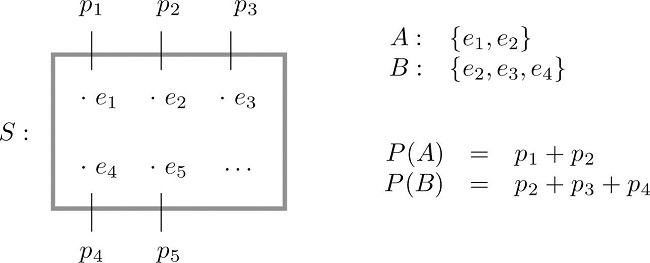
Since the whole sample space \(S\) is an event that is certain to occur, the sum of the probabilities of all the outcomes must be the number \(1\).
In ordinary language probabilities are frequently expressed as percentages. For example, we would say that there is a \(70\%\) chance of rain tomorrow, meaning that the probability of rain is \(0.70\). We will use this practice here, but in all the computational formulas that follow we will use the form \(0.70\) and not \(70\%\).
Example \(\PageIndex{5}\)
A coin is called “balanced” or “fair” if each side is equally likely to land up. Assign a probability to each outcome in the sample space for the experiment that consists of tossing a single fair coin.
With the outcomes labeled \(h\) for heads and \(t\) for tails, the sample space is the set
\[S=\{h,t\} \nonumber \]
Since the outcomes have the same probabilities, which must add up to \(1\), each outcome is assigned probability \(1/2\).
Example \(\PageIndex{6}\)
A die is called “balanced” or “fair” if each side is equally likely to land on top. Assign a probability to each outcome in the sample space for the experiment that consists of tossing a single fair die. Find the probabilities of the events \(E\): “an even number is rolled” and \(T\): “a number greater than two is rolled.”
With outcomes labeled according to the number of dots on the top face of the die, the sample space is the set
\[S=\{1,2,3,4,5,6\} \nonumber \]
Since there are six equally likely outcomes, which must add up to \(1\), each is assigned probability \(1/6\).
Since \(E = \{2,4,6\}\),
\[P(E) = \dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{6} = \dfrac{3}{6} = \dfrac{1}{2} \nonumber \]
Since \(T = \{3,4,5,6\}\),
\[P(T) = \dfrac{4}{6} = \dfrac{2}{3} \nonumber \]
Example \(\PageIndex{7}\)
Two fair coins are tossed. Find the probability that the coins match, i.e., either both land heads or both land tails.
In Example \(\PageIndex{3}\) we constructed the sample space \(S=\{2h,2t,d\}\) for the situation in which the coins are identical and the sample space \(S′=\{hh,ht,th,tt\}\) for the situation in which the two coins can be told apart.
The theory of probability does not tell us how to assign probabilities to the outcomes, only what to do with them once they are assigned. Specifically, using sample space \(S\), matching coins is the event \(M=\{2h, 2t\}\) which has probability \(P(2h)+P(2t)\). Using sample space \(S'\), matching coins is the event \(M'=\{hh, tt\}\), which has probability \(P(hh)+P(tt)\). In the physical world it should make no difference whether the coins are identical or not, and so we would like to assign probabilities to the outcomes so that the numbers \(P(M)\) and \(P(M')\) are the same and best match what we observe when actual physical experiments are performed with coins that seem to be fair. Actual experience suggests that the outcomes in S' are equally likely, so we assign to each probability \(\frac{1}{4}\), and then...
\[P(M') = P(hh) + P(tt) = \frac{1}{4} + \frac{1}{4} = \frac{1}{2} \nonumber \]
Similarly, from experience appropriate choices for the outcomes in \(S\) are:
\[P(2h) = \frac{1}{4} \nonumber \]
\[P(2t) = \frac{1}{4} \nonumber \]
\[P(d) = \frac{1}{2} \nonumber \]
The previous three examples illustrate how probabilities can be computed simply by counting when the sample space consists of a finite number of equally likely outcomes. In some situations the individual outcomes of any sample space that represents the experiment are unavoidably unequally likely, in which case probabilities cannot be computed merely by counting, but the computational formula given in the definition of the probability of an event must be used.
Example \(\PageIndex{8}\)
The breakdown of the student body in a local high school according to race and ethnicity is \(51\%\) white, \(27\%\) black, \(11\%\) Hispanic, \(6\%\) Asian, and \(5\%\) for all others. A student is randomly selected from this high school. (To select “randomly” means that every student has the same chance of being selected.) Find the probabilities of the following events:
- \(B\): the student is black,
- \(M\): the student is minority (that is, not white),
- \(N\): the student is not black.
The experiment is the action of randomly selecting a student from the student population of the high school. An obvious sample space is \(S=\{w,b,h,a,o\}\). Since \(51\%\) of the students are white and all students have the same chance of being selected, \(P(w)=0.51\), and similarly for the other outcomes. This information is summarized in the following table:
\[\begin{array}{l|cccc}Outcome & w & b & h & a & o \\ Probability & 0.51 & 0.27 & 0.11 & 0.06 & 0.05\end{array} \nonumber \]
- Since \(B=\{b\},\; \; P(B)=P(b)=0.27\)
- Since \(M=\{b,h,a,o\},\; \; P(M)=P(b)+P(h)+P(a)+P(o)=0.27+0.11+0.06+0.05=0.49\)
- Since \(N=\{w,h,a,o\},\; \; P(N)=P(w)+P(h)+P(a)+P(o)=0.51+0.11+0.06+0.05=0.73\)
Example \(\PageIndex{9}\)
The student body in the high school considered in the last example may be broken down into ten categories as follows: \(25\%\) white male, \(26\%\) white female, \(12\%\) black male, \(15\%\) black female, 6% Hispanic male, \(5\%\) Hispanic female, \(3\%\) Asian male, \(3\%\) Asian female, \(1\%\) male of other minorities combined, and \(4\%\) female of other minorities combined. A student is randomly selected from this high school. Find the probabilities of the following events:
- \(B\): the student is black
- \(MF\): the student is a non-white female
- \(FN\): the student is female and is not black
Now the sample space is \(S=\{wm, bm, hm, am, om, wf, bf, hf, af, of\}\). The information given in the example can be summarized in the following table, called a two-way contingency table:
| Gender | Race / Ethnicity | ||||
|---|---|---|---|---|---|
| White | Black | Hispanic | Asian | Others | |
| Male | 0.25 | 0.12 | 0.06 | 0.03 | 0.01 |
| Female | 0.26 | 0.15 | 0.05 | 0.03 | 0.04 |
- Since \(B=\{bm, bf\},\; \; P(B)=P(bm)+P(bf)=0.12+0.15=0.27\)
- Since \(MF=\{bf, hf, af, of\},\; \; P(M)=P(bf)+P(hf)+P(af)+P(of)=0.15+0.05+0.03+0.04=0.27\)
- Since \(FN=\{wf, hf, af, of\},\; \; P(FN)=P(wf)+P(hf)+P(af)+P(of)=0.26+0.05+0.03+0.04=0.38\)
Key Takeaway
- The sample space of a random experiment is the collection of all possible outcomes.
- An event associated with a random experiment is a subset of the sample space.
- The probability of any outcome is a number between \(0\) and \(1\). The probabilities of all the outcomes add up to \(1\).
- The probability of any event \(A\) is the sum of the probabilities of the outcomes in \(A\).
Probability of Simple Events
Students also viewed
Probability Worksheets
- Kindergarten
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Methodology
- Random Assignment in Experiments | Introduction & Examples
Random Assignment in Experiments | Introduction & Examples
Published on March 8, 2021 by Pritha Bhandari . Revised on June 22, 2023.
In experimental research, random assignment is a way of placing participants from your sample into different treatment groups using randomization.
With simple random assignment, every member of the sample has a known or equal chance of being placed in a control group or an experimental group. Studies that use simple random assignment are also called completely randomized designs .
Random assignment is a key part of experimental design . It helps you ensure that all groups are comparable at the start of a study: any differences between them are due to random factors, not research biases like sampling bias or selection bias .
Table of contents
Why does random assignment matter, random sampling vs random assignment, how do you use random assignment, when is random assignment not used, other interesting articles, frequently asked questions about random assignment.
Random assignment is an important part of control in experimental research, because it helps strengthen the internal validity of an experiment and avoid biases.
In experiments, researchers manipulate an independent variable to assess its effect on a dependent variable, while controlling for other variables. To do so, they often use different levels of an independent variable for different groups of participants.
This is called a between-groups or independent measures design.
You use three groups of participants that are each given a different level of the independent variable:
- a control group that’s given a placebo (no dosage, to control for a placebo effect ),
- an experimental group that’s given a low dosage,
- a second experimental group that’s given a high dosage.
Random assignment to helps you make sure that the treatment groups don’t differ in systematic ways at the start of the experiment, as this can seriously affect (and even invalidate) your work.
If you don’t use random assignment, you may not be able to rule out alternative explanations for your results.
- participants recruited from cafes are placed in the control group ,
- participants recruited from local community centers are placed in the low dosage experimental group,
- participants recruited from gyms are placed in the high dosage group.
With this type of assignment, it’s hard to tell whether the participant characteristics are the same across all groups at the start of the study. Gym-users may tend to engage in more healthy behaviors than people who frequent cafes or community centers, and this would introduce a healthy user bias in your study.
Although random assignment helps even out baseline differences between groups, it doesn’t always make them completely equivalent. There may still be extraneous variables that differ between groups, and there will always be some group differences that arise from chance.
Most of the time, the random variation between groups is low, and, therefore, it’s acceptable for further analysis. This is especially true when you have a large sample. In general, you should always use random assignment in experiments when it is ethically possible and makes sense for your study topic.
Prevent plagiarism. Run a free check.
Random sampling and random assignment are both important concepts in research, but it’s important to understand the difference between them.
Random sampling (also called probability sampling or random selection) is a way of selecting members of a population to be included in your study. In contrast, random assignment is a way of sorting the sample participants into control and experimental groups.
While random sampling is used in many types of studies, random assignment is only used in between-subjects experimental designs.
Some studies use both random sampling and random assignment, while others use only one or the other.

Random sampling enhances the external validity or generalizability of your results, because it helps ensure that your sample is unbiased and representative of the whole population. This allows you to make stronger statistical inferences .
You use a simple random sample to collect data. Because you have access to the whole population (all employees), you can assign all 8000 employees a number and use a random number generator to select 300 employees. These 300 employees are your full sample.
Random assignment enhances the internal validity of the study, because it ensures that there are no systematic differences between the participants in each group. This helps you conclude that the outcomes can be attributed to the independent variable .
- a control group that receives no intervention.
- an experimental group that has a remote team-building intervention every week for a month.
You use random assignment to place participants into the control or experimental group. To do so, you take your list of participants and assign each participant a number. Again, you use a random number generator to place each participant in one of the two groups.
To use simple random assignment, you start by giving every member of the sample a unique number. Then, you can use computer programs or manual methods to randomly assign each participant to a group.
- Random number generator: Use a computer program to generate random numbers from the list for each group.
- Lottery method: Place all numbers individually in a hat or a bucket, and draw numbers at random for each group.
- Flip a coin: When you only have two groups, for each number on the list, flip a coin to decide if they’ll be in the control or the experimental group.
- Use a dice: When you have three groups, for each number on the list, roll a dice to decide which of the groups they will be in. For example, assume that rolling 1 or 2 lands them in a control group; 3 or 4 in an experimental group; and 5 or 6 in a second control or experimental group.
This type of random assignment is the most powerful method of placing participants in conditions, because each individual has an equal chance of being placed in any one of your treatment groups.
Random assignment in block designs
In more complicated experimental designs, random assignment is only used after participants are grouped into blocks based on some characteristic (e.g., test score or demographic variable). These groupings mean that you need a larger sample to achieve high statistical power .
For example, a randomized block design involves placing participants into blocks based on a shared characteristic (e.g., college students versus graduates), and then using random assignment within each block to assign participants to every treatment condition. This helps you assess whether the characteristic affects the outcomes of your treatment.
In an experimental matched design , you use blocking and then match up individual participants from each block based on specific characteristics. Within each matched pair or group, you randomly assign each participant to one of the conditions in the experiment and compare their outcomes.
Sometimes, it’s not relevant or ethical to use simple random assignment, so groups are assigned in a different way.
When comparing different groups
Sometimes, differences between participants are the main focus of a study, for example, when comparing men and women or people with and without health conditions. Participants are not randomly assigned to different groups, but instead assigned based on their characteristics.
In this type of study, the characteristic of interest (e.g., gender) is an independent variable, and the groups differ based on the different levels (e.g., men, women, etc.). All participants are tested the same way, and then their group-level outcomes are compared.
When it’s not ethically permissible
When studying unhealthy or dangerous behaviors, it’s not possible to use random assignment. For example, if you’re studying heavy drinkers and social drinkers, it’s unethical to randomly assign participants to one of the two groups and ask them to drink large amounts of alcohol for your experiment.
When you can’t assign participants to groups, you can also conduct a quasi-experimental study . In a quasi-experiment, you study the outcomes of pre-existing groups who receive treatments that you may not have any control over (e.g., heavy drinkers and social drinkers). These groups aren’t randomly assigned, but may be considered comparable when some other variables (e.g., age or socioeconomic status) are controlled for.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Student’s t -distribution
- Normal distribution
- Null and Alternative Hypotheses
- Chi square tests
- Confidence interval
- Quartiles & Quantiles
- Cluster sampling
- Stratified sampling
- Data cleansing
- Reproducibility vs Replicability
- Peer review
- Prospective cohort study
Research bias
- Implicit bias
- Cognitive bias
- Placebo effect
- Hawthorne effect
- Hindsight bias
- Affect heuristic
- Social desirability bias
In experimental research, random assignment is a way of placing participants from your sample into different groups using randomization. With this method, every member of the sample has a known or equal chance of being placed in a control group or an experimental group.
Random selection, or random sampling , is a way of selecting members of a population for your study’s sample.
In contrast, random assignment is a way of sorting the sample into control and experimental groups.
Random sampling enhances the external validity or generalizability of your results, while random assignment improves the internal validity of your study.
Random assignment is used in experiments with a between-groups or independent measures design. In this research design, there’s usually a control group and one or more experimental groups. Random assignment helps ensure that the groups are comparable.
In general, you should always use random assignment in this type of experimental design when it is ethically possible and makes sense for your study topic.
To implement random assignment , assign a unique number to every member of your study’s sample .
Then, you can use a random number generator or a lottery method to randomly assign each number to a control or experimental group. You can also do so manually, by flipping a coin or rolling a dice to randomly assign participants to groups.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bhandari, P. (2023, June 22). Random Assignment in Experiments | Introduction & Examples. Scribbr. Retrieved June 11, 2024, from https://www.scribbr.com/methodology/random-assignment/
Is this article helpful?

Pritha Bhandari
Other students also liked, guide to experimental design | overview, steps, & examples, confounding variables | definition, examples & controls, control groups and treatment groups | uses & examples, what is your plagiarism score.
Help | Advanced Search
Statistics > Machine Learning
Title: generative assignment flows for representing and learning joint distributions of discrete data.
Abstract: We introduce a novel generative model for the representation of joint probability distributions of a possibly large number of discrete random variables. The approach uses measure transport by randomized assignment flows on the statistical submanifold of factorizing distributions, which also enables to sample efficiently from the target distribution and to assess the likelihood of unseen data points. The embedding of the flow via the Segre map in the meta-simplex of all discrete joint distributions ensures that any target distribution can be represented in principle, whose complexity in practice only depends on the parametrization of the affinity function of the dynamical assignment flow system. Our model can be trained in a simulation-free manner without integration by conditional Riemannian flow matching, using the training data encoded as geodesics in closed-form with respect to the e-connection of information geometry. By projecting high-dimensional flow matching in the meta-simplex of joint distributions to the submanifold of factorizing distributions, our approach has strong motivation from first principles of modeling coupled discrete variables. Numerical experiments devoted to distributions of structured image labelings demonstrate the applicability to large-scale problems, which may include discrete distributions in other application areas. Performance measures show that our approach scales better with the increasing number of classes than recent related work.
| Subjects: | Machine Learning (stat.ML); Machine Learning (cs.LG) |
| Cite as: | [stat.ML] |
| (or [stat.ML] for this version) | |
| Focus to learn more arXiv-issued DOI via DataCite |
Submission history
Access paper:.
- HTML (experimental)
- Other Formats
References & Citations
- Google Scholar
- Semantic Scholar
BibTeX formatted citation
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

IMAGES
VIDEO
COMMENTS
Simple probability. Jake is going to call one person from his contacts at random. He has 30 total contacts. 16 of those contacts are people he met at school. What is P (call a person from school) ? If necessary, round your answer to 2 decimal places. Learn for free about math, art, computer programming, economics, physics, chemistry, biology ...
The relative frequency approach involves taking the follow three steps in order to determine P ( A ), the probability of an event A: Perform an experiment a large number of times, n, say. Count the number of times the event A of interest occurs, call the number N ( A ), say. Then, the probability of event A equals: P ( A) = N ( A) n.
Practice Activities for Simple Probability. I'm always looking for practice activities that match the assessment I'll be giving students at the end of the unit. Here are a few activities that kids love and that give them a lot of practice with simple probability: QR Code Game. Kids love QR Codes.
Classical Probability (Equally Likely Outcomes): To find the probability of an event happening, you divide the number of ways the event can happen by the total number of possible outcomes. Probability of an Event Not Occurring: If you want to find the probability of an event not happening, you subtract the probability of the event happening from 1.
Unit 7: Probability. 0/1600 Mastery points. Basic theoretical probability Probability using sample spaces Basic set operations Experimental probability. Randomness, probability, and simulation Addition rule Multiplication rule for independent events Multiplication rule for dependent events Conditional probability and independence.
The probability of an event is a number between 0 and 1 (inclusive). If the probability of an event is 0, then the event is impossible. On the other hand, an event with probability 1 is certain to occur. In general, the higher the probability of an event, the more likely it is that the event will occur.
SECTION 8.1 PROBLEM SET: SAMPLE SPACES AND PROBABILITY. In problems 1 - 6, write a sample space for the given experiment. 1) A die is rolled. 2) A penny and a nickel are tossed. 3) A die is rolled, and a coin is tossed. 4) Three coins are tossed. 5) Two dice are rolled. 6) A jar contains four marbles numbered 1, 2, 3, and 4.
Probability tells us how often some event will happen after many repeated trials. You've experienced probability when you've flipped a coin, rolled some dice, or looked at a weather forecast. Go deeper with your understanding of probability as you learn about theoretical, experimental, and compound probability, and investigate permutations, combinations, and more!
This video provides an introduction to probability. It explains how to calculate the probability of an event occurring in addition to determining the sample...
Probability With a Pair of Dice Worksheet These Probability Worksheets will produce problems with simple numbers, sums, differences, multiples, divisors, and factors using a pair of dice. Probability With a Deck of Cards Worksheet These Probability Worksheets will produce problems about a standard 52 card deck without the Jokers.
Probability law: An assignment of probabilities to events in a mathematically consistent way EE 178/278A: Basic Probability Page 1-6. Discrete Sample Spaces • Sample space is called discrete if it contains a countable number of sample points • Examples: Flip a coin once: Ω = {H,T}
Probability of Simple Events. Practice finding the probability of simple events with this one-page worksheet! Geared toward seventh-grade learners, this worksheet gives students hands-on practice calculating simple probabilities in the context of real-world scenarios. Learners are presented with six relatable problems about movies, restaurants ...
A basic probability assignment is a mapping m from the set of all subsets of a universal finite nonempty set X to the interval ... and outcomes, standard decision principles apply. For example, in special cases a simple comparison of possible outcomes indicates a preference between a pair of options. If, for example, the outcome of one option ...
Basic probability worksheets for beginners in 6th grade and 7th grade to understand the different type of events such as more likely, less likely, equally likely and so on. Balls in container. Identify suitable events. Mutually inclusive and exclusive events. Free probability worksheets for kids include odds, spinner problems, coins, deck of ...
Probability. Probability means possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one. Probability has been introduced in Maths to predict how likely events are to happen. The meaning of probability is basically the extent to which something is likely to happen.
Tutorial on finding the probability of an event. In what follows, S is the sample space of the experiment in question and E is the event of interest. n(S) is the number of elements in the sample space S and n(E) is the number of elements in the event E. . Questions and their Solutions Question 1 A die is rolled, find the probability that an even number is obtained.
experiment and what probability would you assign to the simple events. 2. A coin is biased in such a way that a head is twice as likely to come up as a tails. Determine a probability assignment for the simple events of the sample space S ={H,T} that reflects this bias. 3. A die is rolled 1000 times with the results given in the table.
Example 1- Probability Using a Die. Given a standard die, determine the probability for the following events when rolling the die one time: P (5) P (even number) P (7) Before we start the solution, please take note that: P (5) means the probability of rolling a 5. When you see P ( ) this means to find the probability of whatever is indicated ...
Probability organized? In this topic, students conduct simple experiments and determine theoretical and experimental probabilities of simple events. They use familiar objects, such as number cubes and spinners, to learn the terminology of probability, including outcome, experiment, sample space, event, simple event, probability, complementary
Simple Probability Experiments . The topic area of probability provides a good opportunity for students to engage in practical work as a means of gaining an understanding of the basic principles of probability. This resource package contains a variety of activities providing opportunity for students to record and describe the outcomes of simple ...
The sample space of a random experiment is the collection of all possible outcomes. An event associated with a random experiment is a subset of the sample space. The probability of any outcome is a number between [Math Processing Error] and [Math Processing Error]. The probabilities of all the outcomes add up to [Math Processing Error].
12/21. Mr. Tindel will randomly choose a student from his class as the student council representative. There are 12 girls and 9 boys in his class. What is the probability Mr. Tindel will not choose a boy? 1/2. Terry placed 6 number tiles labeled 4, 7, 10, 11, 14, and 21 in a box. He will pick one of the number tiles from the box without looking.
× Description: "This worksheet is designed to introduce children to the concept of basic probability through practical examples leveraging dice and spinners. It comprises 12 engaging and thought-provoking math problems, teaching them about odds, event likelihood, and random selection. The worksheet is versatile in its application, allowing for customization, conversion into flashcards, and ...
Probability sampling is a sampling method that involves randomly selecting a sample, or a part of the population that you want to research. It is also sometimes called random sampling. To qualify as being random, each research unit (e.g., person, business, or organization in your population) must have an equal chance of being selected.
Random sampling (also called probability sampling or random selection) is a way of selecting members of a population to be included in your study. In contrast, random assignment is a way of sorting the sample participants into control and experimental groups. While random sampling is used in many types of studies, random assignment is only used ...
View PDF HTML (experimental) Abstract: We introduce a novel generative model for the representation of joint probability distributions of a possibly large number of discrete random variables. The approach uses measure transport by randomized assignment flows on the statistical submanifold of factorizing distributions, which also enables to sample efficiently from the target distribution and to ...