Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.
- View all journals

Pure mathematics articles from across Nature Portfolio
Pure mathematics uses mathematics to explore abstract ideas, mathematics that does not necessarily describe a real physical system. This can include developing the fundamental tools used by mathematicians, such as algebra and calculus, describing multi-dimensional space, or better understanding the philosophical meaning of mathematics and numbers themselves.
Latest Research and Reviews
Various distance between generalized Diophantine fuzzy sets using multiple criteria decision making and their real life applications
- Murugan Palanikumar
- Nasreen Kausar
- Fikadu Tesgera Tolasa

AI-driven research in pure mathematics and theoretical physics
Advances in artificial-intelligence-assisted mathematical investigations suggest that human–machine collaboration will be an integral part of future theoretical research.
- Yang-Hui He
High accuracy solutions for the Pochhammer–Chree equation in elastic media
- Mostafa M. A. Khater
- Suleman H. Alfalqi
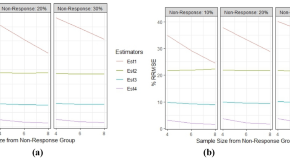
Calibration estimation of population total using multi-auxiliary information in the presence of non-response
- Anant Patel
- Menakshi Pachori
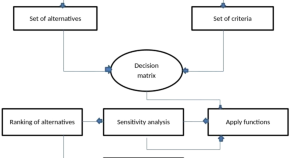
Optimizing decision-making with aggregation operators for generalized intuitionistic fuzzy sets and their applications in the tech industry
- Muhammad Wasim
- Awais Yousaf
- Hamiden Abd El-Wahed Khalifa
A new multi-attribute group decision-making method based on Einstein Bonferroni operators under interval-valued Fermatean hesitant fuzzy environment
- Jasni Mohamad Zain
News and Comment

The real value of numbers
- Mark Buchanan
Machine learning to guide mathematicians
- Fernando Chirigati
A different perspective on the history of the proof of Hall conductance quantization
- Matthew B. Hastings


e is everywhere
From determining the compound interest on borrowed money to gauging chances at the roulette wheel in Monte Carlo, Stefanie Reichert explains that there’s no way around Euler’s number.
- Stefanie Reichert
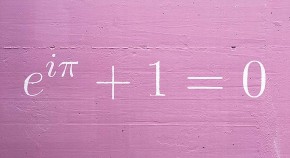
Imagination captured
Imaginary numbers have a chequered history, and a sparse — if devoted — following. Abigail Klopper looks at why a concept as beautiful as i gets such a bad rap.
- Abigail Klopper
Prime interference
- David Abergel
Quick links
- Explore articles by subject
- Guide to authors
- Editorial policies
- Welcome from the Chair
- Michalik Distinguished Lecture Series
- Pittsburgh Mathematical Horizons Lecture Series
- Open Faculty Positions
- Advising & Support
- Calculus Curriculum
- Degree Programs/Requirements
- Extracurricular Activities
- Math Placement Assessment
- Math Assistance Center/Posvar Computing Lab
- Research/Career Opportunities
- Study Abroad
- Admissions & Financial Aid
- Degree Programs
- Graduate Employment
- Graduate Handbook
- Information for Incoming Graduate Students
- Organizations
- Research Opportunities
- Teaching Opportunities
Research Areas
- Graduate Research
- Undergraduate Research
- Mathematics Research Center
- Technical Reports
- Publications
- Gallery of Research Images
- Faculty Admin
- Adjunct Faculty
- Part-Time Faculty
- Emeritus Faculty
- Post-Doctoral Associates
- Graduate Students
- Stay in Touch
- Newsletter Archive
- Upcoming Events
- Past Events
- Prospective Students

Department members engage in cutting-edge research on a wide variety of topics in mathematics and its applications. Topics continually evolve to reflect emerging interests and developments, but can roughly grouped into the following areas.
Algebra, Combinatorics, and Geometry
Algebra, combinatorics, and geometry are areas of very active research at the University of Pittsburgh.
Analysis and Partial Differential Equations
The research of the analysis group covers functional analysis, harmonic analysis, several complex variables, partial differential equations, and analysis on metric and Carnot-Caratheodory spaces.
Applied Analysis
The department is a leader in the analysis of systems of nonlinear differential equations and dynamical systems that arise in modeling a variety of physical phenomena. They include problems in biology, chemistry, phase transitions, fluid flow, flame propagation, diffusion processes, and pattern formation in nonlinear stochastic partial differential equations.
Mathematical Biology
The biological world stands as the next great frontier for mathematical modeling and analysis. This group studies complex systems and dynamics arising in various biological phenomena.
Mathematical Finance
A rapidly growing area of mathematical finance is Quantitative Behavioral Finance. The high-tech boom and bust of the late 1990s followed by the housing and financial upheavals of 2008 have made a convincing case for the necessity of adopting broader assumptions in finance.
Numerical Analysis and Scientific Computing
The diversity of this group is reflected in its research interests: numerical analysis of partial differential equations , adaptive methods for scientific computing, computational methods of fluid dynamics and turbulence, numerical solution of nonlinear problems arising from porous media flow and transport, optimal control, and simulation of stochastic reaction diffusion systems.
Topology and Differential Geometry
Research in analytic topology continues in the broad area of generalized metric spaces. This group studies relativity theory and differential geometry, with emphasis on twistor methods, as well as geometric and topological aspects of quantum field theory, string theory, and M-theory.

IMAGES
VIDEO