
Home → Features → Resources → Metascience

What does 5-sigma mean in science?
In science, there's no room for certainty. But we can get close enough by using statistical significance.

When doing science, you can never afford certainties. A skeptical outlook will always do you good but if this is the case how can scientists tell if their results are significant in the first place? Well, instead of relying on gut feeling, any researcher that’s worth his salt will let the data speak for itself. Namely, a result will be meaningful if it’s statistically significant. But in order for a statistical result to be significant for everyone involved, you also need a standard to measure things.
When referring to statistical significance, the unit of measurement of choice is the standard deviation. Typically denoted by the lowercase Greek letter sigma (σ), this term describes how much variability there is in a given set of data, around a mean, or average, and can be thought of as how “wide” the distribution of points or values is. Samples with a high standard deviation are considered to be more spread out, meaning it has more variability and the results are more interpretable. A low standard deviation, however, revolves more tightly around the mean.
Roll the dice
To understand how scientists use the standard deviation in their work, it helps to consider a familiar statistical example: the coin toss. The coin only has two sides, heads or tails, so the probability of getting one side of the other following a toss is 50 percent. If you flip a coin 100 times, though, chances are you won’t get 50 instances of heads and 50 of tails. Rather, you’ll likely get something like 49 vs 51. If you repeat this 100-coin-toss test another 100 times, you’ll get even more interesting results. Sometimes you’ll get something like 45 vs 55 and in a couple of extreme cases 20 vs 80.
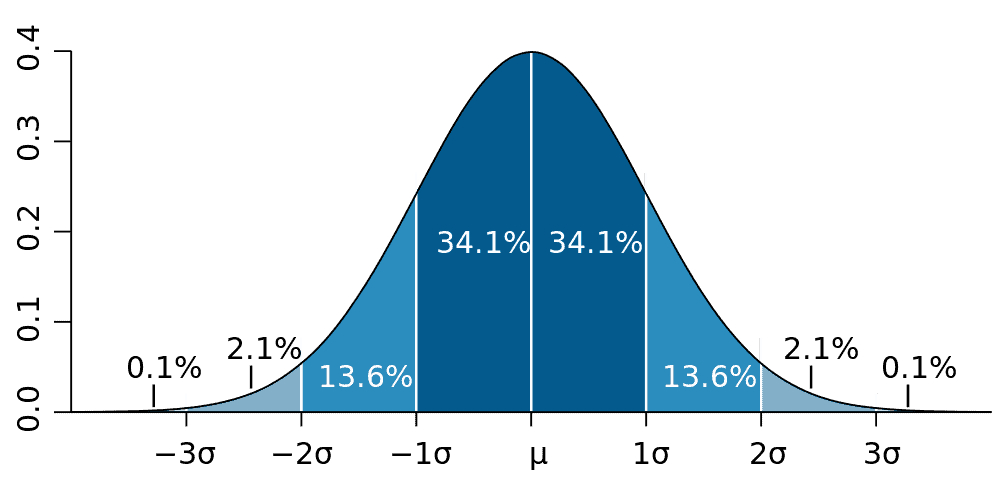
If you plot all of these coin-toss tests on a graph, you should typically see a bell-shaped curve with the highest point of the curve in the middle, tapering off on both sides. This is what you’d call a normal distribution, while the deviation is how far a given point is from the average.
One standard deviation or one-sigma, plotted either above or below the average value, includes 68 percent of all data points. Two-sigma includes 95 percent and three-sigma includes 99.7 percent. Higher sigma values mean that the discovery is less and less likely to be accidentally a mistake or ‘random chance’.
Here’s another way to look at it. The mean human IQ is 100. Data suggests 68 percent of the population are in what is called one standard deviation from the mean (one-sigma) and 27.2 percent of the population are two standard deviations from the mean, being either bright or rather intellectually challenged depending on the side of the bell curve they are on. About 2.1 percent of the population is 3 standard deviations from the mean (3-sigma) — these are brilliant people. Around 0.1% of the population is 4 standard deviations from the mean, the geniuses.
[panel style=”panel-info” title=”Worthy mention: the p-value” footer=””]
The standard deviation becomes an essential tool when testing the likelihood of a hypothesis. Typically, what scientists do is they construct two hypotheses, one where let’s say two phenomena A and B are not connected (the null hypothesis) and one where A and B are connected (the research hypothesis).
What scientists do is they first assume the null hypothesis is true, because that’s the most intellectually conservative thing to do, and then calculate the probability of obtaining data as extreme as the kind they’re observing. This calculation renders the p-value. A p-value close to zero signals that your null hypothesis is false, and typically that a difference is very likely to exist. Large p-values (p is expressed as a value between 0 and 1) imply that there is no detectable difference for the sample size used. A p-value of .05, for example, indicates that you would have only a 5% chance of drawing the sample being tested if the null hypothesis was actually true. Depending on the field, typically psychology and other social sciences, you’ll see papers use the p-value to illustrate statistical significance while maths and physics will employ sigma.
Don’t be so sure
Sometimes just two standard deviations above or below the average, which gives a 95 percent confidence level, is reasonable. Two-sigma is, in fact, standard practice among pollsters and the deviation is directly related to that “margin of sampling error” you’ll often hear reporters mention — in this case it’s 3 percent. If a poll found that 55 percent of the entire population favors candidate A, then 95 percent of the time, a second poll that samples the same number of (random) people will find candidate A is favored somewhere between 52 and 58 percent.
The table below summarizes various σ levels down to two decimal places.
| σ | Confidence that result is real |
|---|---|
| 1σ | 84.13% |
| 1.5 σ | 93.32% |
| 2 σ | 97.73% |
| 2.5 σ | 99.38% |
| 3 σ | 99.87% |
| 3.5 σ | 99.98% |
| > 4 σ | 100% ( ) |
For some fields of science, however, 2-sigma isn’t enough, nor 3 or 4-sigma for that matter. In particle physics, for instance, scientists work with million or even billions of data points, each corresponding to a high energy proton collision. In 2012, CERN researchers reported the discovery of the Higgs boson and press releases tossed the term 5-sigma around. Five-sigma corresponds to a p-value, or probability, of 3×10 -7 , or about 1 in 3.5 million. This is where you need to put your thinking caps on because 5-sigma doesn’t mean there’s a 1 in 3.5 million chance that the Higgs boson is real or not. Rather, it means that if the Higgs boson doesn’t exist (the null hypothesis) there’s only a 1 in 3.5 million chance the CERN data is at least as extreme as what they observed.
Sometimes 5-sigma isn’t enough to be ‘super sure’ of a result. Not even six sigma, which roughly translates to one chance in half a billion that a result is a random fluke. Case in point, in 2011 another experiment from CERN called OPERA found that nearly massless neutrinos travel faster than light . This claim, which bore 6-sigma confidence, was rightfully controversial because it directly violates Einstein’s principle of relativity which says the speed of light is constant to all observers and nothing can travel faster than it. Later , four independent experiments failed to come up with the same level of confidence and OPERA scientists think their original measurement can be written off as owing to a faulty element of the experiment’s fiber-optic timing system.
So bear in mind, just because a result falls inside an accepted interval for significance, that doesn’t necessarily make it truly significant. Context matters, especially if your results are breaking the laws of known physics.
Was this helpful?
Related posts.
- How culture migrated and expanded from city to city in the past 2,000 years
- Beautiful people earn $250,000 extra on average
- This man played the guitar as doctors removed a tumor from his brain
- Amateur paleontologist finds nearly complete 70-million-year-old massive Titanosaur while walking his dog
Recent news

Time ticks slightly faster on the Moon by 57 microseconds. Here’s why this is a big deal

Could autism be linked to gut microbes— and can we use poop for diagnosis?

Yes, Hurricane Beryl is also linked with climate change
- Editorial Policy
- Privacy Policy and Terms of Use
- How we review products
© 2007-2023 ZME Science - Not exactly rocket science. All Rights Reserved.
- Science News
- Environment
- Natural Sciences
- Matter and Energy
- Quantum Mechanics
- Thermodynamics
- Periodic Table
- Applied Chemistry
- Physical Chemistry
- Biochemistry
- Microbiology
- Plants and Fungi
- Planet Earth
- Earth Dynamics
- Rocks and Minerals
- Invertebrates
- Conservation
- Animal facts
- Climate change
- Weather and atmosphere
- Diseases and Conditions
- Mind and Brain
- Food and Nutrition
- Anthropology
- Archaeology
- The Solar System
- Asteroids, meteors & comets
- Astrophysics
- Exoplanets & Alien Life
- Spaceflight and Exploration
- Computer Science & IT
- Engineering
- Sustainability
- Renewable Energy
- Green Living
- Editorial policy
- Privacy Policy
Hypothesis Testing Calculator
| $H_o$: | |||
| $H_a$: | μ | ≠ | μ₀ |
| $n$ | = | $\bar{x}$ | = | = |
| $\text{Test Statistic: }$ | = |
| $\text{Degrees of Freedom: } $ | $df$ | = |
| $ \text{Level of Significance: } $ | $\alpha$ | = |
Type II Error
| $H_o$: | $\mu$ | ||
| $H_a$: | $\mu$ | ≠ | $\mu_0$ |
| $n$ | = | σ | = | $\mu$ | = |
| $\text{Level of Significance: }$ | $\alpha$ | = |
The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.
| $\sigma$ Known | $\sigma$ Unknown | |
| Test Statistic | $ z = \dfrac{\bar{x}-\mu_0}{\sigma/\sqrt{{\color{Black} n}}} $ | $ t = \dfrac{\bar{x}-\mu_0}{s/\sqrt{n}} $ |
Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.
| Lower Tail Test | Upper Tail Test | Two-Tailed Test |
| $H_0 \colon \mu \geq \mu_0$ | $H_0 \colon \mu \leq \mu_0$ | $H_0 \colon \mu = \mu_0$ |
| $H_a \colon \mu | $H_a \colon \mu \neq \mu_0$ |
In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.
To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.
In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.
To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.
| Lower Tail Test | Upper Tail Test | Two-Tailed Test |
| If $z \leq -z_\alpha$, reject $H_0$. | If $z \geq z_\alpha$, reject $H_0$. | If $z \leq -z_{\alpha/2}$ or $z \geq z_{\alpha/2}$, reject $H_0$. |
| If $t \leq -t_\alpha$, reject $H_0$. | If $t \geq t_\alpha$, reject $H_0$. | If $t \leq -t_{\alpha/2}$ or $t \geq t_{\alpha/2}$, reject $H_0$. |
When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.
| Condition | ||||
| $H_0$ True | $H_a$ True | |||
| Conclusion | Accept $H_0$ | Correct | Type II Error | |
| Reject $H_0$ | Type I Error | Correct | ||
Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Help interpreting "five sigma" standard?
So, I am coming from a math/stats background. I was just wondering about this in the abstract, and tried Googling around, and came across this article which says the following regarding some experiments undertaken at CERN:
it is the probability that if the particle does not exist, the data that CERN scientists collected in Geneva, Switzerland, would be at least as extreme as what they observed.
But, "does not exist" doesn't seem to me to be a very well-defined hypothesis to test:
In my understanding of frequentist hypothesis testing, tests are always designed with the intent to provide evidence against a particular hypothesis, in a very Popperian sort of epistemology. It just so happens that in a lot of the toy examples used in stats classes, and also in many real-life instances, the negation of the hypothesis one sets out to prove wrong is itself an interesting hypothesis. E.g. ACME corp hypothesizes that their ACME brand bird seed will attract >90% of roadrunners passing within 5m of a box of it. W.E. Coyote hypothesizes the negation. Either can set about gathering data to provide evidence against the hypothesis of the other, and because the hypotheses are logical negations of one another, evidence against ACME is evidence for W.E.C. and vice versa.
In the quote above, they attempt to frame one hypothesis as "yes Higgs' Boson" and it's negation as "no Higgs' Boson". It seems that if the intent is to provide evidence for "yes Higgs' Boson", then in normal frequentist methodology, one gathers evidence against "no Higgs' Boson" and can quantify that evidence into a p-value or just a number of standard errors of whatever quantity predicted by the theory we happen to be investigating. But this seems to me to be silly, since the negation of the physical model that includes the Higgs' is an infinite space of models. OTOH, this is the only context in which the "five sigma" p-value surrogate seems to make any sense.
In fact, this was my original thought when I set out Googling: the five sigma standard implies that we are gathering evidence against something, but modern physics theories seem to encompass such a breadth, and are yet so specific, that gathering evidence against their bare negation is nonsense.
What am I missing here? What does "five sigma" evidence for the Higgs hypothesis (or other physics hypotheses) mean in this context?
- experimental-physics
- error-analysis
- data-analysis
- $\begingroup$ I suspect that the words right before where you started quoting this are critical. Without reading the article we don't know precisely what "it" is. $\endgroup$ – Brick Commented May 21, 2021 at 13:44
- 1 $\begingroup$ @Brick """In short, five-sigma corresponds to a p-value, or probability, of 3x10-7, or about 1 in 3.5 million. This is not the probability that the Higgs boson does or doesn't exist; rather, it is the probability that if the particle does not exist, the data that CERN scientists collected in Geneva, Switzerland, would be at least as extreme as what they observed.""" $\endgroup$ – Him Commented May 21, 2021 at 13:54
- $\begingroup$ "it" is the five sigma standard, which I suppose in normal frequentist lingo is more akin to "alpha" than a p-value, but /shrug. $\endgroup$ – Him Commented May 21, 2021 at 13:56
- 1 $\begingroup$ It's worth pointing out, I think, that not all data analysis in particle physics is frequentist. Also, if you're already familiar with statistics and want to quickly get familiar with what, specifically, particle physicists are doing, I recommend the particle data group which has many reviews. $\endgroup$ – Richard Myers Commented May 21, 2021 at 20:21
- $\begingroup$ @Him: Actually, no, the "it" at the start of the quote refers to a p-value. Suggest you edit the question to include the full quote. $\endgroup$ – Daniel R. Collins Commented May 22, 2021 at 4:28
4 Answers 4
The Higgs-discovery experiment is a particle-counting experiment. Lots of particles are produced by collisions in the accelerator, and appear in its various detectors. Information about those particles is stored for later: when they appeared, the direction they were traveling, their kinetic energy, their charge, what other particles appeared elsewhere in the detector at the same time. Then you can reconstruct “events,” group them in different ways, and look at them in a histogram, like this one:

[Mea culpa: I remember this image, and others like it, from the Higgs discovery announcement, but I found it from an image search and I don’t have a proper source link.]
These are simultaneous detections of two photons (“diphotons”), grouped by the “equivalent mass” $m_{\gamma\gamma}$ of the pair. There are tons and tons and tons of photons rattling around these collisions, and directional tracking for photons is not very good, so most of these “pairs” are just random coincidences, unrelated photons that happened to reach different parts of the detector at the same time. Because each collision is independent of all the others, the filling of each little bin is subject to Poisson statistics : a bin with $N$ events in it has an intrinsic “one-sigma” statistical uncertainty of $\pm\sqrt N$ . You can see the error bars in the total-minus-fit plot in the bottom panel: on the left side, where $N\approx 6000$ events per interval in the top figure, the error bars are roughly $\sqrt{6000}\approx 80$ events; on the right side, where there is less signal, the error bars are appropriately smaller.
The “one-sigma” confidence limit is 68%. Therefore, if those data were really independently generated by a Poissonian process whose average behavior were described by the fit line, you would expect the data points to be equally distributed above and below the fit, with about 68% of the error bars crossing the fit line. The other third-ish will miss the fit line, just from ordinary noise. In this plot we have thirty points, and about ten of them have error bars that don’t cross the fit line: totally reasonable. On average one point in twenty should be, randomly, two or more error bars away from the prediction (or, “two sigma” corresponds to a 95% confidence limit).
There are two remarkable bins in this histogram, centered on 125 GeV and 127 GeV, which are different from the background fit by (reading by eye) approximately $180\pm60$ and $260\pm60$ events. The “null hypothesis” is that these two differences, roughly $3\sigma$ and $4\sigma$ , are both statistical flukes, just like the low bin at 143 GeV is probably a statistical fluke. You can see that this null hypothesis is strongly disfavored, relative to the hypothesis that “in some collisions, an object with mass near 125 GeV decays into two photons.”
This diphoton plot by itself doesn’t get you to a five-sigma discovery: that required data in multiple different Higgs decay channels, combined from both of the big CERN experiments, which required a great deal of statistical sophistication. An important part of the discovery was combining the data from all channels to determine the best estimate for the Higgs’s mass, charge, and spin. Another important result out of the discover was the relative intensities of the different decay modes. As another answer says, it helped a lot that we already had a prediction there might be a particle with this mass. But I think this data set shows the null hypothesis nicely: most of ATLAS’s photon pairs come from a well-defined continuum background of accidental coincidences, and the null hypothesis is that there’s nothing special about any of the photon pairs which happen to have an equivalent mass of 125 GeV.
- $\begingroup$ Nice answer; I have a query about the red line on the graph. First, I think it would be appropriate to present the data without such a curve, so as not to pre-judge the issue of whether or not there is a significant bump at 126 GeV. But if we go ahead and fit a peak, then how come the one shown is slightly to the left of the data? It is also a tad too wide I think (compared to a least-squares best fit). $\endgroup$ – Andrew Steane Commented May 26, 2021 at 14:49
- $\begingroup$ @AndrewSteane I think the short answer to your question is that the best-fit mass and decay width for the Higgs aren’t a fit to just this diphoton data, but at the same time to other Higgs decay channels. (The long answer is probably “read the discovery papers.”) I agree with you that a best fit for these data alone would probably have the peak a little narrower and at slightly higher mass. But, in the spirit of this answer about the null hypothesis, I think you would also agree that the red curve is in no way excluded. $\endgroup$ – rob ♦ Commented May 26, 2021 at 17:37
I think this question may arise from a difference between somewhat rough layman's-terms presentations and the more careful statistics which goes on in the actual labs. But even after a given body of data has been analyzed to death, there is no formal way to capture in full the evidence underlying the way knowledge of physics grows. The evidence surrounding the Higgs mechanism, for example, would not be nearly as convincing if the Higgs mechanism itself were not an elegant combination of ideas which already find their place in a coherent whole.
The hypothesis that one is gathering evidence against is always the hypothesis that we are mistaken as to how a given body of data (such as a peak in a spectrum) came about. The mistake could be quite simple, as for example when in fact the underlying distribution is flat and the peak is an artifact of random noise. But usually one has to consider the possibility that the peak is there but is owing to something else than the mechanism under study. The hypothesis one is testing in the strict sense---the sense of ruling out at some level of confidence---is the set of all other ways we have thought of yet as to how the data could arise. In this set of ways we only need to consider ways that reflect known physics and known amounts of noise etc. in the apparatus.
I think what the community of physicists do is a bit like Sherlock Holmes: we try to think of plausible other ways the data could arise, and then give reasons as to why those other ways can be ruled out. The final step, where we proceed to the claim that the leading candidate explanation is what really happened, is not a step that can be quantified by any statistical measure. This is because it relies not only on a given data set, but also on a judgement about the quality of the theory under consideration.
The null hypothesis here is that the data was generated by physics which obeys the effective field theory describing all the Standard Model particles except the Higgs. This model doesn't usually have a name, but could reasonably be called the 'Standard Model without Higgs'. It's a perfectly good effective field theory. It's predictions are barely different from the usual Standard Model (with Higgs).
Asking for a 5 sigma rejection of the null hypothesis in this case means accumulating a lot of data which is incompatible with the 'Standard Model without Higgs". Enough data that a couple of 1 sigma experimental errors don't ruin the result.
- $\begingroup$ And of course the alternative hypothesis is that the data was generated by physics obeying the effective field theory we call the Standard Model. $\endgroup$ – user1504 Commented May 21, 2021 at 15:23
- $\begingroup$ "barely different" I think that maybe something surrounding this statement is actually the crux of the matter. This theory is "barely different" is 99.99999% of ways, but is " very different" in this one particular prediction that we've decided to measure. The discussion with @RogerVadim has me thinking that the implication is that "Standard model with Higgs" is considered to be " very different" in this particular way from any sensible extensions of the "Standard Model without Higgs" that might be reasonably considered actually different theories from the "Standard Model with Higgs" $\endgroup$ – Him Commented May 21, 2021 at 15:32
- $\begingroup$ @Him I'm afraid I can't parse your last sentence. $\endgroup$ – user1504 Commented May 21, 2021 at 17:01
- $\begingroup$ my point here is that "the effective field theory describing all the Standard Model particles except the Higgs" is not a theory. It is a set of theories. There are many possible extensions of the Standard Model that may include a spike in particle event frequency at a given energy. Not all of those are sensible extensions. For example, the "Standard Model with 7TeV magical nano wizard". Not all of them are really different from "Standard Model with Higgs". For example, the "Standard Model with Biggs particle that is just like Higgs but with a "B"" $\endgroup$ – Him Commented May 21, 2021 at 17:32
- $\begingroup$ So, in this sense, even though "Standard Model without Higgs" is an infinite set of models, we say that we've got "five sigma" evidence against them all because we've got "five sigma" evidence against the subset of those hypotheses that we have imagined so far, and which are reasonable according to our current understanding of physics, and are not essentially equivalent to "Standard Model with Higgs" $\endgroup$ – Him Commented May 21, 2021 at 17:37
Refresher on hypothesis testing In (frequentist) hypothesis testing one always have (at least) two hypotheses: the null hypothesis , and the alternative hypothesis . Then p-value is the probability of observing certain dataset, given that the null hypothesis is true, whereas the power of the test is the probability that the alternative hypothesis is true, given the observed data.
If p-value is smaller than a pre-defined threshold ( significance level ), one rejects the null hypothesis as improbable. In the example given in the OP the data is supposed to follow the Gaussian/normal distribution, and five sigma determines the significance level in terms of this distribution (a rather stringent one).
What does it have to do with Popper? From statistical viewpoint, Popperian epistemiology simply means that designing a test to reject a hypothesis and calculating its p-value is usually easier than calculating the test power (which typically requires some ad-hoc assumptions about the underlying probability distributions). In other words, disproving the null hypothesis is easier than proving that the alternative hypothesis is correct. One then chooses the null hypothesis in such a way that it can be disproved, rather than trying to prove it. Choosing whether the particle exists as the null hypothesis and particle does not exist as the alternative one, or vice versa, depends not on the philosophical meaning of either statement, but on our ability to disprove it.
Remark In my opinion the chapter on statistical testing published by the Particle Data Group is one of the best crash courses on statistics for physicists.
- $\begingroup$ My point is that "particle does not exist" is not a physical model that makes a prediction that can be disproved. How can one possibly provide evidence against this statement? $\endgroup$ – Him Commented May 21, 2021 at 14:23
- $\begingroup$ @Him We are talking here about the experimental measurements: we observe certain results and explain them using a theory that assumes that the particle does not exists. E.g., two particles come into collision, and one can assume that they annihilate OR that they combine into a new particle. In some cases writing down a theory for two particles annihilating and testing it is easier, than designing a description fo a completely unnown particle. $\endgroup$ – Roger V. Commented May 21, 2021 at 14:29
- $\begingroup$ So, the "five sigma" interpretation is the normal one, and the evidence provided is, in fact, against some other well-defined model that makes a measurable prediction. I suppose that this is considered strong evidence for the Higgs theory because it is the only known competing theory, and there currently exists no evidence against the Higgs theory? $\endgroup$ – Him Commented May 21, 2021 at 14:35
- $\begingroup$ One cannot prove Higgs theory... but one coudl disprove the theory that assumes that there is no Higgs particle. And the probability that we are mistaken (p-value) is so small that it is negligieable for all practical purposes. $\endgroup$ – Roger V. Commented May 21, 2021 at 14:37
- 2 $\begingroup$ @Him: The null hypothesis was that there wasn't a particle of the approximate mass. This was rejected to 5-sigma confidence. The initial discovery was of such a particle of such mass; further arguments were used to make the case that the particle was the Higgs. This article kinda talks about it. $\endgroup$ – Nat Commented May 22, 2021 at 15:12
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged experimental-physics error-analysis statistics data-analysis or ask your own question .
- Featured on Meta
- We spent a sprint addressing your requests — here’s how it went
- Upcoming initiatives on Stack Overflow and across the Stack Exchange network...
Hot Network Questions
- Do provisional utility patent applications also contain claims?
- Combinatoric Problem in Stardew Valley about Keg Layout
- Does the damage from Thunderwave occur before or after the target is moved
- Why bother with planetary battlefields?
- Are the North Star and the moon ever visible in the night sky at the same time?
- Why is this outlet required to be installed on at least 10 meters of wire?
- Does the cosmological constant entail a mass for the graviton?
- French Election 2024 - seat share based on first round only
- Assigning unique ID to new points in QGIS
- Is it an option for the ls utility specified in POSIX.1-2017?
- Filled in \diamond without XeLaTeX
- To overlay two curves from a plot
- Search and replace multiple characters simultaneously
- How are GameManagers created in Unity?
- Is it possible to go back to the U.S. after overstaying as a child?
- Why is this transformer placed on rails?
- Is the variance of the mean of a set of possibly dependent random variables less than the average of their respective variances?
- Should I apologise to a professor after a gift authorship attempt, which they refused?
- How can I prove that '+' is same as max?
- Can a MicroSD card help speed up my Mini PC?
- iMac 21" i3 very slow even on clean install of OS
- Can trills have 3 notes instead of two?
- Simple BJT circuit problem
- Judging a model through the TP, TN, FP, and FN values
CERN Accelerating science

Why do physicists mention “five sigma” in their results?

When a new particle physics discovery is made, you may have heard the term “sigma” being used. What does this mean? Why is it so important to talk about sigma when making a claim for a new particle discovery? And why is five sigma in particular so important?
Why does particle physics rely on statistics?
Particles produced in collisions in the Large Hadron Collider (LHC) are tiny and extremely short-lived. Because they almost immediately decay into further particles, it is impossible for physicists to directly “see” them. Instead, they look at the properties of the final particles, such as their charge, mass, spin and velocity. They work like detectives: the end products provide clues to the possible transformations that the particles underwent as they decayed. The probabilities of these so-called “decay channels” are predicted by theory.
In the LHC, millions of particle collisions per second are tracked by the detectors and filtered through trigger systems to identify decays of rare particles. Scientists then analyse the filtered data to look for anomalies, which can indicate new physics.
As with any experiment, there is always a chance of error. Background noise can cause natural fluctuations in the data resulting in statistical error. There is also potential for error if there isn’t enough data, or systematic error caused by faulty equipment or small mistakes in calculations. Scientists look for ways to reduce the impact of these errors to ensure that the claims they make are as accurate as possible.
What is statistical significance?
Imagine rolling a standard die. There is a one in six probability of getting one number. Now imagine rolling two dice – the probability of getting a certain total number varies – there is only one way to roll a two, and six different ways to roll a seven. If you were to roll two dice many, many times and record your results, the shape of the graph would follow a bell-curve known as a normal distribution.
The normal distribution has some interesting properties. It is symmetrical, its peak is called the mean and the data spread is measured using standard deviation. For data that follows a normal distribution, the probability of a data point being within one standard deviation of the mean value is 68%, within two is 95%, within three is even higher.
Standard deviation is represented by the Greek letter σ, or sigma. Measured by numbers of standard deviations from the mean, statistical significance is how far away a certain data point lies from its expected value.
What has this got to do with physics?
When scientists record data from the LHC, it is natural that there are small bumps and statistical fluctuations, but these are generally close to the expected value. There is an indication of a new result when there is a larger anomaly. At which point can this anomaly be classified as a new phenomenon? Scientists use statistics to find this out.
Imagine the dice metaphor again. Except this time, you are rolling one die, but you do not know if it is weighted. You roll it once and get a three. There is nothing particularly significant about this – there was a one in six chance of your result – you need more data to determine if it is weighted. You roll it twice, three times, or even more, and every time it lands on a three. At what point can you confirm it is weighted?
There isn’t a particular rule for this, but after around eight times of getting the same number, you’d be pretty certain that it was. The chance of this happening as a fluke is only (1/6) 8 = 0.00006%.
In the same way, this is how physicists determine if an anomaly is indeed a result. With more and more data, the likelihood of a statistical fluctuation at a specific point gets smaller and smaller. In the case of the Higgs boson , physicists needed enough data for the statistical significance to pass the threshold of five sigma. Only then could they announce the discovery of “a Higgs-like particle.”
What does it mean when physicists say data has a statistical significance of five sigma?
A result that has a statistical significance of five sigma means the almost certain likelihood that a bump in the data is caused by a new phenomenon, rather than a statistical fluctuation. Scientists calculate this by measuring the signal against the expected fluctuations in the background noise across the whole range. For some results, whose anomalies could lie in either direction above or below the expected value, a significance of five sigma is the 0.00006% chance the data is fluctuation. For other results, like the Higgs boson discovery, a five-sigma significance is the 0.00003% likelihood of a statistical fluctuation, as scientists look for data that exceeds the five-sigma value on one half of the normal distribution graph.

Why is five sigma specifically important for particle physics?
In most areas of science that use statistical analysis, the five-sigma threshold seems overkill. In a population study, such as polls for how people will vote, usually a result with three sigma statistical significance would suffice. However, when discussing the very fabric of the Universe, scientists aim to be as precise as possible. The results of the fundamental nature of matter are high impact and have significant repercussions if they are wrong.
In the past, physicists have noticed results that could indicate new discoveries, with the data having only three to four sigma statistical significance. These have often been disproven as more data is collected.
If there is a systematic error, such as a miscalculation, the high initial significance of five sigma may mean that the results are not completely void. However, this means that the result is not definite and cannot be used to make a claim for a new discovery.
Five sigma is considered the “gold standard” in particle physics because it guarantees an extremely low likelihood of a claim being false.
But not all five sigmas are equal…
Five sigma is generally the accepted value for statistical significance for finding new particles within the Standard Model – those particles that are predicted by theory and lie within our current understanding of nature. Five sigma significance is also accepted when searching for specific properties of particle behaviour, as there is less chance of finding fluctuations elsewhere in the range.
Whether five sigma is enough statistical significance can be determined by comparing the probability of the new hypothesis with the chance it is a statistical fluctuation, taking the theory into account.
For physics beyond the Standard Model, or data that contradicts generally accepted physics, a much higher value of statistical significance is required – effectively enough to “disprove” the previous physics. In his paper “ The significance of five sigma, ” physicist Louis Lyons suggests that results for more unlikely phenomena should have a higher statistical significance, such as seven sigma for the detection of gravitational waves or the discovery of pentaquarks.
In this paper, Lyons also deems five sigma statistical significance to be enough for the Higgs boson discovery. This is because the theory for the Higgs boson had been predicted, mathematically tested, and generally accepted by the particle physics community well-before the LHC could generate conditions to be able to observe it. But once this was achieved, it still required a high statistical significance to determine if the signal detected was indeed a discovery.
___________________________________________________________________________
A statistical significance of five sigma is rigorous, but it is really a minimum. A higher value for statistical significance cements data as being more reliable. However, achieving results with statistical significance of six, seven, or even eight sigma requires a lot more data, a lot more time, and a lot more energy. In other words, a probability of at most 0.00006% that a new phenomenon is not a statistical fluke is good enough.
Find out more:
- Paper: The significance of five sigma
- Video: The Higgs boson discovery, explained
- Online article: One and two sided probability
Facts and figures about the LHC
Is the large hadron collider dangerous, how do i visit cern.
- A too-brief and too-long introduction to statistics
- “We’re looking for a five-sigma effect”
- View page source
“We’re looking for a five-sigma effect”
Suppose after a long and detailed physics analysis, you finally have a result. Assume it’s in the form of a measurement and its associated error. 1 Let’s further assume that there’s a null hypothesis associated with this measurement: If a particular property did not exist, the measurement would have been different.

Figure 88: https://xkcd.com/892/ by Randall Munroe
When physicists consider such a measurement, they ask the question: What is the probability is that their measurement is consistent with the null hypothesis; that is, what are the chances that the null hypothesis is correct, and that their measurement is just a random statistical fluctuation?
Let’s take another look at our friend, the Gaussian function. As a probability distribution, it indicates the likelihood of a particular measurement being different from the actual underlying value.

Figure 89: A plot of the normal distribution where each band has a width of 1 standard deviation. Source: M. W. Toews , under the CC-by-4.0 license
Think about this in the context of the following cartoon. The scientists perform 20 tests each with a significance at the 5% level. You’d expect that one of the tests would randomly be far enough from the “mean of the normal distribution” that you’d get an anomalous result. Physicists often can’t perform multiple measurements of a given quantity, 2 so they look at their results in a different way.

Figure 90: https://xkcd.com/882/ by Randall Munroe
When physicists express a measurement versus a null hypothesis, they usually state it in terms of “sigma” or the number of standard deviations that it is from that hypothesis. This is how I think of it, even though they don’t usually show it in this way:

Figure 91: What I picture when a physicist says they’ve observed an effect at more than a 5 \(\sigma\) level of significance.
In this imaginary experiment, the result is reported at 22.01 ± 3.52 WeV . I picture a normal distribution with a mean of 22.01 and \(\sigma\) =3.52 superimposed on the measurement. Then I count off the number of sigmas between the mean and the null hypothesis. In this particular imaginary experiment, the difference is more than 5 \(\sigma\) and therefore refutes the null hypothesis. Hence the P particle exists!
In other words, I imagine an assumption that the same normal distribution applies to the null hypothesis (the dashed curve) and ask if what we actually observed could be within 5 \(\sigma\) of the mean of the null hypothesis.
At this point, you may have compared Figure 89 and Figure 91 , including the captions, and thought, “Wait a second. A 3 \(\sigma\) effect would mean that the odds that the null hypothesis was correct would be something like 0.1%, right? In fact, I just looked it up, and the exact value is closer to 0.3%. Isn’t that good enough? It’s much better than that xkcd cartoon. Why do physicists insist on a 5 \(\sigma\) effect, which is around 0.00003% or one in 3.5 million?”
A 3 \(\sigma\) effect is indeed only considered “evidence,” while a 5 \(\sigma\) effect is necessary for a “discovery.” The reason why is summarized in a quote from a colleague on my thesis experiment: “We see 3 \(\sigma\) effects go away all the time.”
The reason why 3 \(\sigma\) effects “go away” is a deeper study of the data and its analysis procedure. One potential cause of such a shift is a change in systematic bias as you work to understand your Systematic errors .
Figure 92: https://xkcd.com/2118/ by Randall Munroe
As you’ll learn in the section on Systematic errors , the errors are the tough part.
The Large Hadron Collider at CERN costs about $9 billion. It’s obvious that they should build 100 similar nine-mile-wide particle colliders so we can make multiple independent measurements of the Higgs boson mass. Why they haven’t is completely beyond me.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Null and Alternative Hypotheses | Definitions & Examples
Null & Alternative Hypotheses | Definitions, Templates & Examples
Published on May 6, 2022 by Shaun Turney . Revised on June 22, 2023.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :
- Null hypothesis ( H 0 ): There’s no effect in the population .
- Alternative hypothesis ( H a or H 1 ) : There’s an effect in the population.
Table of contents
Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, similarities and differences between null and alternative hypotheses, how to write null and alternative hypotheses, other interesting articles, frequently asked questions.
The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”:
- The null hypothesis ( H 0 ) answers “No, there’s no effect in the population.”
- The alternative hypothesis ( H a ) answers “Yes, there is an effect in the population.”
The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample. It’s critical for your research to write strong hypotheses .
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.
Prevent plagiarism. Run a free check.
The null hypothesis is the claim that there’s no effect in the population.
If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.
Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept . Be careful not to say you “prove” or “accept” the null hypothesis.
Null hypotheses often include phrases such as “no effect,” “no difference,” or “no relationship.” When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).
You can never know with complete certainty whether there is an effect in the population. Some percentage of the time, your inference about the population will be incorrect. When you incorrectly reject the null hypothesis, it’s called a type I error . When you incorrectly fail to reject it, it’s a type II error.
Examples of null hypotheses
The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.
| ( ) | ||
| Does tooth flossing affect the number of cavities? | Tooth flossing has on the number of cavities. | test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ . |
| Does the amount of text highlighted in the textbook affect exam scores? | The amount of text highlighted in the textbook has on exam scores. | : There is no relationship between the amount of text highlighted and exam scores in the population; β = 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression.* | test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ . |
*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .
The alternative hypothesis ( H a ) is the other answer to your research question . It claims that there’s an effect in the population.
Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.
The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
Alternative hypotheses often include phrases such as “an effect,” “a difference,” or “a relationship.” When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes < or >). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.
Examples of alternative hypotheses
The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.
| Does tooth flossing affect the number of cavities? | Tooth flossing has an on the number of cavities. | test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ . |
| Does the amount of text highlighted in a textbook affect exam scores? | The amount of text highlighted in the textbook has an on exam scores. | : There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression. | test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < . |
Null and alternative hypotheses are similar in some ways:
- They’re both answers to the research question.
- They both make claims about the population.
- They’re both evaluated by statistical tests.
However, there are important differences between the two types of hypotheses, summarized in the following table.
| A claim that there is in the population. | A claim that there is in the population. | |
|
| ||
| Equality symbol (=, ≥, or ≤) | Inequality symbol (≠, <, or >) | |
| Rejected | Supported | |
| Failed to reject | Not supported |
To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.
General template sentences
The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:
Does independent variable affect dependent variable ?
- Null hypothesis ( H 0 ): Independent variable does not affect dependent variable.
- Alternative hypothesis ( H a ): Independent variable affects dependent variable.
Test-specific template sentences
Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.
| ( ) | ||
| test
with two groups | The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ . | The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ . |
| with three groups | The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ . | The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population. |
| There is no correlation between independent variable and dependent variable in the population; ρ = 0. | There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0. | |
| There is no relationship between independent variable and dependent variable in the population; β = 0. | There is a relationship between independent variable and dependent variable in the population; β ≠ 0. | |
| Two-proportions test | The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = . | The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ . |
Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (“ x affects y because …”).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses . In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Turney, S. (2023, June 22). Null & Alternative Hypotheses | Definitions, Templates & Examples. Scribbr. Retrieved July 8, 2024, from https://www.scribbr.com/statistics/null-and-alternative-hypotheses/
Is this article helpful?

Shaun Turney
Other students also liked, inferential statistics | an easy introduction & examples, hypothesis testing | a step-by-step guide with easy examples, type i & type ii errors | differences, examples, visualizations, what is your plagiarism score.
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 : The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 . This is usually what the researcher is trying to prove.
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject H 0 " if the sample information favors the alternative hypothesis or "do not reject H 0 " or "decline to reject H 0 " if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example 9.1
H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ .30 H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
Example 9.2
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are: H 0 : μ = 2.0 H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 66
- H a : μ __ 66
Example 9.3
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are: H 0 : μ ≥ 5 H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 45
- H a : μ __ 45
Example 9.4
In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p __ 0.40
- H a : p __ 0.40
Collaborative Exercise
Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/introductory-statistics-2e/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Introductory Statistics 2e
- Publication date: Dec 13, 2023
- Location: Houston, Texas
- Book URL: https://openstax.org/books/introductory-statistics-2e/pages/1-introduction
- Section URL: https://openstax.org/books/introductory-statistics-2e/pages/9-1-null-and-alternative-hypotheses
© Dec 6, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

IMAGES
VIDEO
COMMENTS
The null hypothesis really should be the theoretical predictions about the particle under test though, not the nonexistence of a particle. The problem is that sometimes there are no real predictions, so that gets conveniently ignored.
Rather, it means that if the Higgs boson doesn’t exist (the null hypothesis) there’s only a 1 in 3.5 million chance the CERN data is at least as extreme as what they observed.
The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page. The easy-to-use hypothesis testing calculator gives you step-by-step solutions to the test statistic, p-value, critical value and more.
The null hypothesis here is that the data was generated by physics which obeys the effective field theory describing all the Standard Model particles except the Higgs. This model doesn't usually have a name, but could reasonably be called the 'Standard Model without Higgs'.
In his paper “The significance of five sigma,” physicist Louis Lyons suggests that results for more unlikely phenomena should have a higher statistical significance, such as seven sigma for the detection of gravitational waves or the discovery of pentaquarks.
When physicists consider such a measurement, they ask the question: What is the probability is that their measurement is consistent with the null hypothesis; that is, what are the chances that the null hypothesis is correct, and that their measurement is just a random statistical fluctuation?
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test: Null hypothesis (H0): There’s no effect in the population. Alternative hypothesis (Ha or H1): There’s an effect in the population.
They are called the null hypothesis and the alternative hypothesis. These hypotheses contain opposing viewpoints. \(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
To test a null hypothesis, find the p -value for the sample data and graph the results. When deciding whether or not to reject the null the hypothesis, keep these two parameters in mind: \alpha > p-value, reject the null hypothesis. \alpha \leq p-value, do not reject the null hypothesis.
The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis.