presentation group theory

Group Presentation

Examples of group presentations include the following.

3. Coxeter groups .

4. Braid groups .

This entry contributed by Yves de Cornulier

Explore with Wolfram|Alpha

More things to try:

• zero element
• Cayley graph
• 30-level 12-ary tree

Referenced on Wolfram|Alpha

Cite this as:.

de Cornulier, Yves . "Group Presentation." From MathWorld --A Wolfram Web Resource, created by Eric W. Weisstein . https://mathworld.wolfram.com/GroupPresentation.html

Subject classifications

Presentation of Groups

Cite this chapter.

• Richard H. Crowell 4 &
• Ralph H. Fox 5  

Part of the book series: Graduate Texts in Mathematics ((GTM,volume 57))

2659 Accesses

In this chapter we give a firm foundation to the concept of defining a group by generators and relations. This is an important step; for example, if one is not careful to distinguish between the elements of a group and the words that describe these elements, utter confusion is likely to ensue.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or Ebook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime
• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Unable to display preview.  Download preview PDF.

There are a number of similar problems which are known to have no general solution: deciding whether or not the group defined by a given presentation is trivial (the triviality problem), is finite, is abelian, is free, etc; deciding whether or not a given word is a consequence of a given set of words (the word problem); and many others. See M. O. Rabin, “Recursive Unsolvability of Group Theoretic Problems,” Annals of Mathematics , Vol. 67 (1958), pp. 172–194.

Article   MathSciNet   MATH   Google Scholar  

Download references

Author information

Authors and affiliations.

Department of Mathematics, Dartmouth College, Hanover, New Hampshire, 03755, USA

Richard H. Crowell

Princeton University, Princeton, New Jersey, USA

Ralph H. Fox

You can also search for this author in PubMed   Google Scholar

Rights and permissions

Reprints and permissions

Copyright information

© 1963 R. H. Crowell and C. Fox

About this chapter

Crowell, R.H., Fox, R.H. (1963). Presentation of Groups. In: Introduction to Knot Theory. Graduate Texts in Mathematics, vol 57. Springer, New York, NY. https://doi.org/10.1007/978-1-4612-9935-6_5

Download citation

DOI : https://doi.org/10.1007/978-1-4612-9935-6_5

Publisher Name : Springer, New York, NY

Print ISBN : 978-1-4612-9937-0

Online ISBN : 978-1-4612-9935-6

eBook Packages : Springer Book Archive

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

The Structure of Groups

In mathematics and abstract algebra, group theory studies the algebraic structures known as groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces, can all be seen as groups endowed with additional operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right.

Various physical systems, such as crystals and the hydrogen atom, may be modelled by symmetry groups. Thus group theory and the closely related representation theory have many important applications in physics, chemistry, and materials science. Group theory is also central to public key cryptography.

The early history of group theory dates from the 19th century. One of the most important mathematical achievements of the 20th century was the collaborative effort, taking up more than 10,000 journal pages and mostly published between 1960 and 1980, that culminated in a complete classification of finite simple groups.

• 1.1 Permutation groups
• 1.2 Matrix groups
• 1.3 Transformation groups
• 1.4 Abstract groups
• 1.5 Groups with additional structure
• 2.1 Finite group theory
• 2.2 Representation of groups
• 2.3 Lie theory
• 2.4 Combinatorial and geometric group theory
• 3 Connection of groups and symmetry
• 4.1 Galois theory
• 4.2 Algebraic topology
• 4.3 Algebraic geometry
• 4.4 Algebraic number theory
• 4.5 Harmonic analysis
• 4.6 Combinatorics
• 4.8 Physics
• 4.9 Chemistry and materials science
• 4.10 Cryptography
• 6 Licensing

Main classes of groups

The range of groups being considered has gradually expanded from finite permutation groups and special examples of matrix groups to abstract groups that may be specified through a presentation by generators and relations.

Permutation groups

The first class of groups to undergo a systematic study was permutation groups. Given any set X and a collection G of bijections of X into itself (known as permutations ) that is closed under compositions and inverses, G is a group acting on X . If X consists of n elements and G consists of all permutations, G is the symmetric group S n ; in general, any permutation group G is a subgroup of the symmetric group of X . An early construction due to Cayley exhibited any group as a permutation group, acting on itself ( X = G ) by means of the left regular representation.

In many cases, the structure of a permutation group can be studied using the properties of its action on the corresponding set. For example, in this way one proves that for n ≥ 5, the alternating group A n is simple, i.e. does not admit any proper normal subgroups. This fact plays a key role in the impossibility of solving a general algebraic equation of degree n ≥ 5 in radicals.

Matrix groups

The next important class of groups is given by matrix groups , or linear groups. Here G is a set consisting of invertible matrices of given order n over a field K that is closed under the products and inverses. Such a group acts on the n -dimensional vector space K n by linear transformations. This action makes matrix groups conceptually similar to permutation groups, and the geometry of the action may be usefully exploited to establish properties of the group G .

Transformation groups

Permutation groups and matrix groups are special cases of transformation groups: groups that act on a certain space X preserving its inherent structure. In the case of permutation groups, X is a set; for matrix groups, X is a vector space. The concept of a transformation group is closely related with the concept of a symmetry group: transformation groups frequently consist of all transformations that preserve a certain structure.

The theory of transformation groups forms a bridge connecting group theory with differential geometry. A long line of research, originating with Lie and Klein, considers group actions on manifolds by homeomorphisms or diffeomorphisms. The groups themselves may be discrete or continuous.

Abstract groups

Most groups considered in the first stage of the development of group theory were "concrete", having been realized through numbers, permutations, or matrices. It was not until the late nineteenth century that the idea of an abstract group as a set with operations satisfying a certain system of axioms began to take hold. A typical way of specifying an abstract group is through a presentation by generators and relations ,

A significant source of abstract groups is given by the construction of a factor group , or quotient group, G / H , of a group G by a normal subgroup H . Class groups of algebraic number fields were among the earliest examples of factor groups, of much interest in number theory. If a group G is a permutation group on a set X , the factor group G / H is no longer acting on X ; but the idea of an abstract group permits one not to worry about this discrepancy.

The change of perspective from concrete to abstract groups makes it natural to consider properties of groups that are independent of a particular realization, or in modern language, invariant under isomorphism, as well as the classes of group with a given such property: finite groups, periodic groups, simple groups, solvable groups, and so on. Rather than exploring properties of an individual group, one seeks to establish results that apply to a whole class of groups. The new paradigm was of paramount importance for the development of mathematics: it foreshadowed the creation of abstract algebra in the works of Hilbert, Emil Artin, Emmy Noether, and mathematicians of their school.

Groups with additional structure

An important elaboration of the concept of a group occurs if G is endowed with additional structure, notably, of a topological space, differentiable manifold, or algebraic variety. If the group operations m (multiplication) and i (inversion),

are compatible with this structure, that is, they are continuous, smooth or regular (in the sense of algebraic geometry) maps, then G is a topological group, a Lie group, or an algebraic group.

The presence of extra structure relates these types of groups with other mathematical disciplines and means that more tools are available in their study. Topological groups form a natural domain for abstract harmonic analysis, whereas Lie groups (frequently realized as transformation groups) are the mainstays of differential geometry and unitary representation theory. Certain classification questions that cannot be solved in general can be approached and resolved for special subclasses of groups. Thus, compact connected Lie groups have been completely classified. There is a fruitful relation between infinite abstract groups and topological groups: whenever a group Γ can be realized as a lattice in a topological group G , the geometry and analysis pertaining to G yield important results about Γ . A comparatively recent trend in the theory of finite groups exploits their connections with compact topological groups (profinite groups): for example, a single p -adic analytic group G has a family of quotients which are finite p -groups of various orders, and properties of G translate into the properties of its finite quotients.

Branches of group theory

Finite group theory.

During the twentieth century, mathematicians investigated some aspects of the theory of finite groups in great depth, especially the local theory of finite groups and the theory of solvable and nilpotent groups. As a consequence, the complete classification of finite simple groups was achieved, meaning that all those simple groups from which all finite groups can be built are now known.

During the second half of the twentieth century, mathematicians such as Chevalley and Steinberg also increased our understanding of finite analogs of classical groups, and other related groups. One such family of groups is the family of general linear groups over finite fields. Finite groups often occur when considering symmetry of mathematical or physical objects, when those objects admit just a finite number of structure-preserving transformations. The theory of Lie groups, which may be viewed as dealing with "continuous symmetry", is strongly influenced by the associated Weyl groups. These are finite groups generated by reflections which act on a finite-dimensional Euclidean space. The properties of finite groups can thus play a role in subjects such as theoretical physics and chemistry.

Representation of groups

Saying that a group G acts on a set X means that every element of G defines a bijective map on the set X in a way compatible with the group structure. When X has more structure, it is useful to restrict this notion further: a representation of G on a vector space V is a group homomorphism:

where GL( V ) consists of the invertible linear transformations of V . In other words, to every group element g is assigned an automorphism ρ ( g ) such that ρ ( g ) ∘ ρ ( h ) = ρ ( gh ) for any h in G .

This definition can be understood in two directions, both of which give rise to whole new domains of mathematics. On the one hand, it may yield new information about the group G : often, the group operation in G is abstractly given, but via ρ , it corresponds to the multiplication of matrices, which is very explicit. On the other hand, given a well-understood group acting on a complicated object, this simplifies the study of the object in question. For example, if G is finite, it is known that V above decomposes into irreducible parts. These parts in turn are much more easily manageable than the whole V (via Schur's lemma).

Given a group G , representation theory then asks what representations of G exist. There are several settings, and the employed methods and obtained results are rather different in every case: representation theory of finite groups and representations of Lie groups are two main subdomains of the theory. The totality of representations is governed by the group's characters. For example, Fourier polynomials can be interpreted as the characters of U(1), the group of complex numbers of absolute value 1 , acting on the L 2 -space of periodic functions.

A Lie group is a group that is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure. Lie groups are named after Sophus Lie, who laid the foundations of the theory of continuous transformation groups. The term groupes de Lie first appeared in French in 1893 in the thesis of Lie's student Arthur Tresse, page 3.

Lie groups represent the best-developed theory of continuous symmetry of mathematical objects and structures, which makes them indispensable tools for many parts of contemporary mathematics, as well as for modern theoretical physics. They provide a natural framework for analysing the continuous symmetries of differential equations (differential Galois theory), in much the same way as permutation groups are used in Galois theory for analysing the discrete symmetries of algebraic equations. An extension of Galois theory to the case of continuous symmetry groups was one of Lie's principal motivations.

Combinatorial and geometric group theory

Combinatorial group theory studies groups from the perspective of generators and relations. It is particularly useful where finiteness assumptions are satisfied, for example finitely generated groups, or finitely presented groups (i.e. in addition the relations are finite). The area makes use of the connection of graphs via their fundamental groups. For example, one can show that every subgroup of a free group is free.

Geometric group theory attacks these problems from a geometric viewpoint, either by viewing groups as geometric objects, or by finding suitable geometric objects a group acts on. The first idea is made precise by means of the Cayley graph, whose vertices correspond to group elements and edges correspond to right multiplication in the group. Given two elements, one constructs the word metric given by the length of the minimal path between the elements. A theorem of Milnor and Svarc then says that given a group G acting in a reasonable manner on a metric space X , for example a compact manifold, then G is quasi-isometric (i.e. looks similar from a distance) to the space X .

Connection of groups and symmetry

Given a structured object X of any sort, a symmetry is a mapping of the object onto itself which preserves the structure. This occurs in many cases, for example

• If X is a set with no additional structure, a symmetry is a bijective map from the set to itself, giving rise to permutation groups.
• If the object X is a set of points in the plane with its metric structure or any other metric space, a symmetry is a bijection of the set to itself which preserves the distance between each pair of points (an isometry). The corresponding group is called isometry group of X .
• If instead angles are preserved, one speaks of conformal maps. Conformal maps give rise to Kleinian groups, for example.

The axioms of a group formalize the essential aspects of symmetry. Symmetries form a group: they are closed because if you take a symmetry of an object, and then apply another symmetry, the result will still be a symmetry. The identity keeping the object fixed is always a symmetry of an object. Existence of inverses is guaranteed by undoing the symmetry and the associativity comes from the fact that symmetries are functions on a space, and composition of functions is associative.

Frucht's theorem says that every group is the symmetry group of some graph. So every abstract group is actually the symmetries of some explicit object.

The saying of "preserving the structure" of an object can be made precise by working in a category. Maps preserving the structure are then the morphisms, and the symmetry group is the automorphism group of the object in question.

Applications of group theory

Applications of group theory abound. Almost all structures in abstract algebra are special cases of groups. Rings, for example, can be viewed as abelian groups (corresponding to addition) together with a second operation (corresponding to multiplication). Therefore, group theoretic arguments underlie large parts of the theory of those entities.

Galois theory

Galois theory uses groups to describe the symmetries of the roots of a polynomial (or more precisely the automorphisms of the algebras generated by these roots). The fundamental theorem of Galois theory provides a link between algebraic field extensions and group theory. It gives an effective criterion for the solvability of polynomial equations in terms of the solvability of the corresponding Galois group. For example, S 5 , the symmetric group in 5 elements, is not solvable which implies that the general quintic equation cannot be solved by radicals in the way equations of lower degree can. The theory, being one of the historical roots of group theory, is still fruitfully applied to yield new results in areas such as class field theory.

Algebraic topology

Algebraic topology is another domain which prominently associates groups to the objects the theory is interested in. There, groups are used to describe certain invariants of topological spaces. They are called "invariants" because they are defined in such a way that they do not change if the space is subjected to some deformation. For example, the fundamental group "counts" how many paths in the space are essentially different. The Poincaré conjecture, proved in 2002/2003 by Grigori Perelman, is a prominent application of this idea. The influence is not unidirectional, though. For example, algebraic topology makes use of Eilenberg–MacLane spaces which are spaces with prescribed homotopy groups. Similarly algebraic K-theory relies in a way on classifying spaces of groups. Finally, the name of the torsion subgroup of an infinite group shows the legacy of topology in group theory.

Algebraic geometry

Algebraic geometry likewise uses group theory in many ways. Abelian varieties have been introduced above. The presence of the group operation yields additional information which makes these varieties particularly accessible. They also often serve as a test for new conjectures. The one-dimensional case, namely elliptic curves is studied in particular detail. They are both theoretically and practically intriguing. In another direction, toric varieties are algebraic varieties acted on by a torus. Toroidal embeddings have recently led to advances in algebraic geometry, in particular resolution of singularities.

Algebraic number theory

Algebraic number theory makes uses of groups for some important applications. For example, Euler's product formula,

captures the fact that any integer decomposes in a unique way into primes. The failure of this statement for more general rings gives rise to class groups and regular primes, which feature in Kummer's treatment of Fermat's Last Theorem.

Harmonic analysis

Analysis on Lie groups and certain other groups is called harmonic analysis. Haar measures, that is, integrals invariant under the translation in a Lie group, are used for pattern recognition and other image processing techniques.

Combinatorics

In combinatorics, the notion of permutation group and the concept of group action are often used to simplify the counting of a set of objects; see in particular Burnside's lemma.

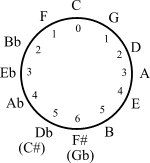
The presence of the 12-periodicity in the circle of fifths yields applications of elementary group theory in musical set theory. Transformational theory models musical transformations as elements of a mathematical group.

In physics, groups are important because they describe the symmetries which the laws of physics seem to obey. According to Noether's theorem, every continuous symmetry of a physical system corresponds to a conservation law of the system. Physicists are very interested in group representations, especially of Lie groups, since these representations often point the way to the "possible" physical theories. Examples of the use of groups in physics include the Standard Model, gauge theory, the Lorentz group, and the Poincaré group.

Group theory can be used to resolve the incompleteness of the statistical interpretations of mechanics developed by Willard Gibbs, relating to the summing of an infinite number of probabilities to yield a meaningful solution.

Chemistry and materials science

In chemistry and materials science, point groups are used to classify regular polyhedra, and the symmetries of molecules, and space groups to classify crystal structures. The assigned groups can then be used to determine physical properties (such as chemical polarity and chirality), spectroscopic properties (particularly useful for Raman spectroscopy, infrared spectroscopy, circular dichroism spectroscopy, magnetic circular dichroism spectroscopy, UV/Vis spectroscopy, and fluorescence spectroscopy), and to construct molecular orbitals.

Molecular symmetry is responsible for many physical and spectroscopic properties of compounds and provides relevant information about how chemical reactions occur. In order to assign a point group for any given molecule, it is necessary to find the set of symmetry operations present on it. The symmetry operation is an action, such as a rotation around an axis or a reflection through a mirror plane. In other words, it is an operation that moves the molecule such that it is indistinguishable from the original configuration. In group theory, the rotation axes and mirror planes are called "symmetry elements". These elements can be a point, line or plane with respect to which the symmetry operation is carried out. The symmetry operations of a molecule determine the specific point group for this molecule.

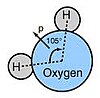
In chemistry, there are five important symmetry operations. They are identity operation ( E) , rotation operation or proper rotation ( C n ), reflection operation ( σ ), inversion ( i ) and rotation reflection operation or improper rotation ( S n ). The identity operation ( E ) consists of leaving the molecule as it is. This is equivalent to any number of full rotations around any axis. This is a symmetry of all molecules, whereas the symmetry group of a chiral molecule consists of only the identity operation. An identity operation is a characteristic of every molecule even if it has no symmetry. Rotation around an axis ( C n ) consists of rotating the molecule around a specific axis by a specific angle. It is rotation through the angle 360°/ n , where n is an integer, about a rotation axis. For example, if a water molecule rotates 180° around the axis that passes through the oxygen atom and between the hydrogen atoms, it is in the same configuration as it started. In this case, n = 2, since applying it twice produces the identity operation. In molecules with more than one rotation axis, the C n axis having the largest value of n is the highest order rotation axis or principal axis. For example in boron trifluoride (BF 3 ), the highest order of rotation axis is C 3 , so the principal axis of rotation is C 3 .

In the reflection operation ( σ ) many molecules have mirror planes, although they may not be obvious. The reflection operation exchanges left and right, as if each point had moved perpendicularly through the plane to a position exactly as far from the plane as when it started. When the plane is perpendicular to the principal axis of rotation, it is called σ h (horizontal). Other planes, which contain the principal axis of rotation, are labeled vertical ( σ v ) or dihedral ( σ d ).

Inversion (i ) is a more complex operation. Each point moves through the center of the molecule to a position opposite the original position and as far from the central point as where it started. Many molecules that seem at first glance to have an inversion center do not; for example, methane and other tetrahedral molecules lack inversion symmetry. To see this, hold a methane model with two hydrogen atoms in the vertical plane on the right and two hydrogen atoms in the horizontal plane on the left. Inversion results in two hydrogen atoms in the horizontal plane on the right and two hydrogen atoms in the vertical plane on the left. Inversion is therefore not a symmetry operation of methane, because the orientation of the molecule following the inversion operation differs from the original orientation. And the last operation is improper rotation or rotation reflection operation ( S n ) requires rotation of  360°/ n , followed by reflection through a plane perpendicular to the axis of rotation.

Cryptography

Very large groups of prime order constructed in elliptic curve cryptography serve for public-key cryptography. Cryptographical methods of this kind benefit from the flexibility of the geometric objects, hence their group structures, together with the complicated structure of these groups, which make the discrete logarithm very hard to calculate. One of the earliest encryption protocols, Caesar's cipher, may also be interpreted as a (very easy) group operation. Most cryptographic schemes use groups in some way. In particular Diffie–Hellman key exchange uses finite cyclic groups. So the term group-based cryptography refers mostly to cryptographic protocols that use infinite nonabelian groups such as a braid group.

Group theory has three main historical sources: number theory, the theory of algebraic equations, and geometry. The number-theoretic strand was begun by Leonhard Euler, and developed by Gauss's work on modular arithmetic and additive and multiplicative groups related to quadratic fields. Early results about permutation groups were obtained by Lagrange, Ruffini, and Abel in their quest for general solutions of polynomial equations of high degree. Évariste Galois coined the term "group" and established a connection, now known as Galois theory, between the nascent theory of groups and field theory. In geometry, groups first became important in projective geometry and, later, non-Euclidean geometry. Felix Klein's Erlangen program proclaimed group theory to be the organizing principle of geometry.

Galois, in the 1830s, was the first to employ groups to determine the solvability of polynomial equations. Arthur Cayley and Augustin Louis Cauchy pushed these investigations further by creating the theory of permutation groups. The second historical source for groups stems from geometrical situations. In an attempt to come to grips with possible geometries (such as euclidean, hyperbolic or projective geometry) using group theory, Felix Klein initiated the Erlangen programme. Sophus Lie, in 1884, started using groups (now called Lie groups) attached to analytic problems. Thirdly, groups were, at first implicitly and later explicitly, used in algebraic number theory.

The different scope of these early sources resulted in different notions of groups. The theory of groups was unified starting around 1880. Since then, the impact of group theory has been ever growing, giving rise to the birth of abstract algebra in the early 20th century, representation theory, and many more influential spin-off domains. The classification of finite simple groups is a vast body of work from the mid 20th century, classifying all the finite simple groups.

Content obtained and/or adapted from:

• Group theory, Wikipedia under a CC BY-SA license

Login Alert

• < Back to search results
• Topics in the Theory of Group Presentations
• Content listing

Topics in the Theory of Group Presentations

Refine listing, actions for selected content:.

• View selected items
• Save to my bookmarks
• Export citations
• Download PDF (zip)
• Save to Kindle
• Save to Dropbox
• Save to Google Drive

Save content to

To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle .

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service .

• D. L. Johnson
• Online ISBN: 9780511629303
• Book DOI: https://doi.org/10.1017/CBO9780511629303

Save Search

You can save your searches here and later view and run them again in "My saved searches".

14 results in Topics in the Theory of Group Presentations

Guide to the literature and references.

• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp 291-300
• Get access Check if you have access via personal or institutional login Log in Register
• Export citation
• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp vii-viii

These notes arose from a course of lectures given to final year and postgraduate students at the University of Nottingham, and comprise a substantially revised and extended version of my earlier contribution to this series. As before, the emphasis is on concrete examples of groups exhibited in their natural settings and thus to demonstrate at a modest level some of the pervasive connections between group theory and other branches of mathematics. Such is the current rate of progress (both upwards and outwards) in combinatorial group theory that no attempt at completeness is feasible, though it is hoped to bring the reader to within hailing distance of the frontiers of research in one ot two places.

My thanks are due to a host of colleagues, students and friends whose names, too numerous to mention here, may be found scattered through the ensuing pages. It is a pleasure to acknowledge a special debt of gratitude to Professor Sandy Green for introducing me to research mathematics, to Dr E.F. Robertson for his encouragement and for help in correcting the proofs, and to Dr H.R. Morton for much valuable advice on the final chapter. My thanks also go to Professor I.M. James for keeping a paternal eye on things, to Mrs Anne Towndrow for typing half the manuscript, and to the staff of Cambridge University Press for their speed and skill in setting the text (especially the other half).

Chapter VII - Small cancellation groups

• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp 212-244

The Moving Finger writes; and, having writ, Moves on: nor all thy Piety nor Wit Shall lure it back to cancel half a Line, Nor all thy Tears wash out a Word of it.

Given a group G = <X|R>, suppose that the relators in R are all cyclically reduced and that R is symmetrized, that is, if r belongs to R, then so do all cyclic conjugates of r and r -1 . Then G satisfies a small cancellation hypothesis if the amount of cancelling in forming any product rs (r,s ∈ R, r ≠ s -1 in F(X)) is limited in one of various senses to be made precise in §24. The formulation of these hypotheses is inspired by the properties of the planar diagrams studied in §23. The latter boast a degree of intrinsic usefulness, and may be thought of as portions of the Cayley diagram of G adapted to fit inside R 2 The power of the hypotheses derives from Euler's formula for planar graphs, which explains the innocent but pervasive topological overtones encountered in this branch of combinatorial group theory.

The conclusions that may be inferred from small cancellation hypotheses form an interrelated hierarchy of properties such as:

G is infinite,

the torsion elements in G can be classified,

G is SQ-universal,’ that is, any countable group can be embedded in some factor group of G,

G contains a non-cyclic free subgroup, and

G has soluble word problem, that is, there is an algorithm for deciding whether or not any given word in F(X) belongs to R.

Chapter V - The triangle groups

• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp 130-146

Chapter III - Groups with few relations

• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp 62-84

Frontmatter

• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp i-iv

Chapter VIII - Groups from topology

• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp 245-290

Nothing puzzles me more than time and space;

and nothing troubles me less, as I never think

about them.

As will already be plain to the erudite reader, the connections between the theory of group presentations and algebraic topology are both substantial and pervasive. Thus, for example, the triangle groups of Chapter V are essentially geometrical objects, homological methods play a crucial role in the theory of group extensions (Chapter VI), and Chapter VII illustrates the dependence of small cancellation methods on properties of planar graphs. The former subject relies on the latter, both for methods and for examples and this interrelationship has been increasingly in evidence since the inception of both.

A vital bond, in one direction at least, is forged by the fundamental group of a space and we begin with a study of this, carrying with us the idea of a surface for a paradigm. Since the theory of compact connected n-manifolds is in a sense algebraically complete when n = 2, we go on to study some examples in the case n = 3. We make no apology for our emphasis on algebraic structure and bias towards computational techniques, nor for the fact that we are merely splashing about on the surface of what are really very deep waters indeed.

• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp v-vi

Index of notation

• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp 301-306

Chapter VI - Extensions of groups

• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp 147-211

… Though with patience He stands waiting, with exactness grinds He all.

The main purpose of this chapter is to give a proof of the celebrated theorem of Golod and Šafarevič, which gives an accurate lower bound for the minimal number r'(G) of relations needed to define a finite p-group G minimally generated by d(G) elements. The naive bound r'(G) ≥ d(G) of Theorem 6.7 is relegated to the humble role of a lemma, to be invoked almost unconsciously in the penultimate line of the proof. The proof we give is due to P. Roquette and is extremely elegant, modulo the rather technical machinery needed to begin it. We shall need the notions of a Gmodule A, and of the cohomology groups H n (G,A), n ∈ N o . If the field k of p-elements is made into a G-module in a trivial way, it turns out that H 1 (G,k) is a vector space over k of dimension d(G), while the dimension r(G) of H 2 (G,k) is at most r'(G). The last fact is proved in Theorem 20.3 using an argument based on the presentation theory of group extensions. Thus we begin with an account of the classical theory of group extensions, and then proceed to establish the connection with group cohomology. The only remaining preliminaries are a localization process and some basic facts about finite p-groups. We conclude by shedding a little light on the unsolved problem of classifying those finite p-groups for which r(G) and r'(G) are equal.

Chapter I - Free groups and free presentations

• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp 1-41

The words are all there ready; now we've got to get them in the right order.

A group G is generated by a subset X if each of its elements can be expressed as a product of members of X ±1 . Such a product is called a word, and a relation is an equation between two words. A set R of relations that hold in G defines the group if every relation that holds in G is a consequence of R. When this happens, we say that G is presented by X and R. This definition is made rigorous using the concept of a free group (essentially, a group having a set of generators between which there are no non-trivial relations), which is defined using a universal property. Having developed some elementary but important properties of free groups (such as their existence), we proceed to the fundamental theorem of §2, where Schreier's proof is given in detail and Nielsen's original method in outline. In §3, the definition of group presentation is made rigorous, and this is used to clarify the proof of the Nielsen-Schreier theorem by means of an anotated example. §4 explains how to pass from a group multiplication table to a presentation and from one presentation to another, as well as describing a presentation for a direct product of two groups.

Elementary properties of free groups

The fundamental notion used in defining presentations of groups is that of a free group. As the definition suggests, the idea of freeness is applicable in algebraic situations other than group theory.

Chapter II - Examples of presentations

• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp 42-61
• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp 307-311

Chapter IV - Presentations of subgroups

• Book: Topics in the Theory of Group Presentations Published online: 28 January 2010 Print publication: 31 July 1980 , pp 85-129

Write the vision, and make it plain upon tables, that he may run that readeth it.

Suppose we are given a presentation <X|R> for a group G. As might be expected, the derivation of a presentation for a specified factor group of G is easy enough (Theorem 3.3). By contrast, the corresponding problem for a subgroup H of G is no simple matter, and is in general very undecidable. As usual we dodge the pathology by confining ourselves to propitious cases, and describe the general method in §12. The whole thing hinges on the derivation of a certain Schreier transversal U, in terms of which we obtain free generators for H (as in Lemma 2.3). A simple trick gives relators for H in terms of the generators X of G and these must be rewritten as words in the free generators of H. If necessary, we can then perform Tietze transformations (Theorem 4.3) on the resulting presentation to reduce it to a more suitable form.

The method of calculating U varies according to what H is and how it is specified. For example, the method of §6 (see Example 6.2) contains an algorithm for computing U in the case where G is finitely generated and H ⊇ G'. The best general method, however, is that invented by J.A. Todd and H.S.M. Coxeter in 1936 and known as coset enumeration. It works in any specific situation when H is the subgroup generated by a set Y of words in X, provided only that |X|, |R|, |Y| and |G:H| are all finite. We describe it in §§10, 11.

Email your librarian or administrator to recommend adding this to your organisation's collection.

nLab group presentation

Group theory.

group theory

• group , ∞-group
• group object , group object in an (∞,1)-category
• abelian group , spectrum
• super abelian group
• group action , ∞-action
• representation , ∞-representation
• homogeneous space

Classical groups

general linear group

unitary group

• special unitary group . projective unitary group

orthogonal group

• special orthogonal group

symplectic group

Finite groups

finite group

symmetric group , cyclic group , braid group

classification of finite simple groups

sporadic finite simple groups

• Monster group , Mathieu group

Group schemes

algebraic group

abelian variety

Topological groups

topological group

compact topological group , locally compact topological group

maximal compact subgroup

string group

compact Lie group

Kac-Moody group

Super-Lie groups

super Lie group

super Euclidean group

Higher groups

• crossed module , strict 2-group

simplicial group

crossed complex

k-tuply groupal n-groupoid

circle n-group , string 2-group , fivebrane Lie 6-group

Cohomology and Extensions

group cohomology

group extension ,

∞-group extension , Ext-group

Related concepts

• quantum group

Presentations of groups

Examples of presentations, the standard presentation, cyclic groups, the symmetric group of order 6, knot groups, coxeter groups, transformations of a group presentation, combinatorial group theory, presentations of monoids and other algebraic and categorical structures..

In trying to study a group G G , one way to proceed is to

look for a set of generating elements;

look for ‘relations’ between those elements.

The problem is partially how one is to interpret this second part. To do this we need to look at words in the generators and hence at the free group on the set of generators.

For example, if we have the symmetric group S 3 S_3 , or, isomorphically, the dihedral group (of symmetries of a triangle) which we will call D 3 D_3 (following the geometric convention (see the Wikipedia article on dihedral groups), then we have 6 elements, and they are all able to be got as products of a transposition and a three cycle (or alternatively as a reflection and a rotation). If we call the three cycle a a and the transposition b b , we have

What about the other words: ba ba for instance. If one calculates b a b a in S 3 S_3 and then looks up what you get you have ba = a 2 b ba = a^2b , so that there is a relation between these two words. This however is not all. What about b a b a a b a a a b b a a b a b a a b a a a b b a a ? That is a word in the a a s and b b s so should represent something in S 3 S_3 . in fact if you think in the geometric interpretation of S 3 S_3 as being the dihedral group, D 3 D_3 , you can pick up a triangle and interpret that word as a list of instructions for moving the triangle. You then find out what this word is out of the 6 possible given forms.

For a presentation, you give a set of generators X X , so there will be an epimorphism from F ( X ) F(X) to G G , and then you try to find a description for the kernel of that epimorphism, which we will denote by N N . The description of this normal subgroup N N is as the normal closure of a set R R of relations, i.e. words in the generators or, equally validly, elements in the free group on X X .

A presentation of a group, G G , is a coequalizer diagram F R ⇉ F X ↠ G F R \rightrightarrows F X \twoheadrightarrow G , where F X F X is the free group on a set of generators , and F R F R one on a set of relations (or relators , depending on how the relations are specified).

This is not quite the usual `classical' form of the definition, so we will take it apart to show the relationship.

A presentation is thus given by a pair of sets, X X and R R , written ⟨ X : R ⟩ \langle X: R\rangle such that setting F = F ( X ) = ⟨ X ⟩ = ⟨ X : ∅ ⟩ F=F(X)= \langle X\rangle =\langle X:\emptyset\rangle to be the free group on the set X X and N N the normal closure of the set of relators R R , there is a specified isomorphism from F / N F/N to G G .

The specified isomorphism is often omitted, as often the set X X of generators is chosen as a subset of the set of elements of G G . In this case, the universal properties of free groups and quotients, there is a unique map F → G F\to G which restricts to the inclusion of X X , and thereby at most one map F / N → G F/N \to G which does so; this map is then the one asserted to be an isomorphism.

In general it is necessary to proceed otherwise, however, and to give a specific function from a set X X to the set of elements of G G . This function then induces a group homomorphism from F = ⟨ X ⟩ F=\langle X\rangle to G G , and if this is a surjection, then we can find some N N (generators for its kernel) to produce a presentation of G G . Without this extra data, certain of the manipulations of a group presntation look decidedly suspect, for instance a substitution which results in two copies of a generator being given. It is also much easier to work with morphisms of presentations if the full data is recorded.

A standard if somewhat trivial example of a presentation is given by the standard presentation of a group, G G . We take X = { x g ∣ g ∈ G , g ≠ 1 } X= \{x_g\mid g\in G,g\neq 1\} , to be a set in bijective correspondence with the underlying set of G G . (You can take X X equal to that set if you like, but sometimes it is better to have a distinct set, for instance, it make for an easier notation for the description of certain morphisms.) The set of relations will be

so as a set is just a copy of G × G G\times G as the relations are indexed by pairs of elements of G G .

Cyclic group, C n C_n , of order n n has presentation ⟨ a : a n ⟩ \langle a : a^n\rangle . There are many different functions from the (singleton) set of generators to C n C_n that will give a suitable presentation in the fuller sense.

The group of permutations of three letters, S 3 S_3 , has a presentation

Here a a corresponds to the 3-cycle, ( 123 ) (123) , whilst b b corresponds to any transposition.

The trefoil knot group has two useful presentations:

⟨ a , b : a 3 = b 2 ⟩ \langle a,b : a^3= b^2\rangle , which displays the fact that the trefoil is a (2,3)- torus knot ; and

⟨ x , y : x y x = y x y ⟩ \langle x,y : x y x = y x y\rangle , which shows the link between this group and the Artin braid group , Br 3 Br3 .

At the entry on Coxeter groups one finds the following:

Definition A Coxeter matrix over an index set I I is a symmetric matrix

such that M ( i , i ) = 1 M(i, i) = 1 for all i ∈ I i \in I , else M ( i , j ) > 1 M(i, j) \gt 1 . Writing m i , j = M ( i , j ) m_{i,j} = M(i, j) , the associated Coxeter group W M W_M is the group presented as having generators s i s_i , i ∈ I i \in I , and relations

for all i , j ∈ I i, j \in I , whenever m i , j ≠ ∞ m_{i, j} \neq \infty . In other words, m i , j m_{i, j} is the order of s i s j s_i s_j (as is easily shown), and these orders determine the group.

We thus have an infinite family of group presentations.

‘Relations’ and ‘relators’ : In the discussion of S 3 S_3 above we had a relation b a = a 2 b b a = a^2b . so we are relating two words of F ( X ) F(X) . It is often the case that instead of relations we use relators , in other words a relation of form r = 1 r = 1 , where r r is a word in the generators. In the example b a = a 2 b b a = a^2b can be easily shown to imply and be implied by a b a b = 1 a b a b = 1 .

Given a group presentation as above, we have a short exact sequence,

where F = F ( X ) F = F(X) , the free group on the set X X , R R is a subset of F F and N = N ( R ) N = N(R) is the normal closure in F F of the set R R . The group F F acts on N N by conjugation: u c = ucu − 1 , for c ∈ N , u ∈ F {}^u c = ucu^{-1}, for c\in N, u \in F and the elements of N N are words in the conjugates of the elements of R R :

where each ε i \varepsilon_i is + 1 + 1 or − 1 - 1 . One also says such elements are consequences of R R . Heuristically an identity among the relations of 𝒫 \mathcal{P} is such an element c c which equals 1.

Given a group presentation, it is natural to perform transformations using substitutions, say adding in one new symbol for a string of generators, and adjusting the presentation accordingly. The valid transformations that do not change the group being presented are formalised as the Tietze transformation s.

The study of group presentations, their transformations etc. forms part of combinatorial group theory .

The theory of group presentations generalises to that of presentations of monoids and then to general rewriting systems.

finitely presentable group

combinatorial group theory

Andrews-Curtis conjecture

Textbook accounts:

Wilhelm Magnus , A. Karras, D. Solitar, Combinatorial group theory: Presentation of groups in terms of generators and relations , Courier Corporation (1966, 2004) [ ISBN:0-486-43830-9 , GoogleBooks ]

David Lawrence Johnson , Topics in Theory of Group Presentations , London Mathematical Society Lecture notes series 42 , Cambridge Univ. Press (1980) [ doi:10.1017/CBO9780511629303 ]

David Lawrence Johnson , Presentations of Groups , London Mathematical Society Student Texts 15 , Cambridge Univ. Press (1990) [ doi:10.1017/CBO9781139168410 ]

N. D. Gilbert and T. Porter , Knots and Surfaces, Oxford U.P., 1994.

In the context of combinatorial group theory :

• Roger C. Lyndon , Paul E. Schupp , Combinatorial group theory , Springer, 1977; toc .

Lecture notes:

• Derek Holt (notes by Florian Bouyer), Presentation of Groups (2013) [ pdf ]

On (finitely) presented groups as fundamental groups of ( finite ) simplicial complexes / CW-complexes :

Joseph J. Rotman , around Thm. 7.34 in: An Introduction to Algebraic Topology , Graduate Texts in Mathematics 119 (1988) [ [ doi:10.1007/978-1-4612-4576-6 ] ]

Behrooz Mashayekhy, Hanieh Mirebrahimi, Some Properties of Finitely Presented Groups with Topological Viewpoints , International Journal of Mathematics, Game Theory and Algebra 18 6 (2010) 511-515 [ arXiv:1012.1744 ]

On rewriting in group presentations:

• Nick Gilbert , Emma Antonia McDougall, Groupoids and the algebra of rewriting in group presentations , Beiträge zur Algebra und Geometrie 62 3 (2021) 1-17 [ doi:10.1007/s13366-020-00531-6 , arXiv:1901.04348 ]

Last revised on April 19, 2023 at 17:47:22. See the history of this page for a list of all contributions to it.

2. Basic Group Theory

May 03, 2013

3.74k likes | 8.91k Views

2. Basic Group Theory. 2.1 Basic Definitions and Simple Examples 2.2 Further Examples, Subgroups 2.3 The Rearrangement Lemma &amp; the Symmetric Group 2.4 Classes and Invariant Subgroups 2.5 Cosets and Factor (Quotient) Groups 2.6 Homomorphisms 2.7 Direct Products.

Share Presentation

• equivalence relation partitions
• invariant subgroup h
• continuous parameters e g
• same length

Presentation Transcript

2. Basic Group Theory 2.1 Basic Definitions and Simple Examples 2.2 Further Examples, Subgroups 2.3 The Rearrangement Lemma & the Symmetric Group 2.4 Classes and Invariant Subgroups 2.5 Cosets and Factor (Quotient) Groups 2.6 Homomorphisms 2.7 Direct Products

2.1 Basic Definitions and Simple Examples Definition 2.1: Group { G, • } is a group if  a , b , c Î G 1. a • b ÎG ( closure ) 2. ( a • b ) • c = a • ( b • c ) ( associativity ) 3. $ e Î G ' e • a = a • e = a ( identity ) 4. $ a–1Î G ' a–1 • a = a • a–1 = e ( inverse ) Definition in terms of multiplication table (abstract group):

Realizations: • {e} = { 1 } Example 1: C1 • Realizations: • {e,a} = { 1, –1} • Reflection group: C = { E, σ } • Rotation group: C2 = { E, C2 } Example 2: C2 Cn = Rotation of angle 2π/n • Realizations: • Rotation group: C3 = { E, C3 , C3–1 } • Cyclic group: C3 = { e, a, a2 ; a3=e } • { 1, e i 2π/3, e i 4π/3 } • Cyclic permutation of 3 objects • { (123), (231), (312) } Example 3: C3 Cyclic group : Cn = { e, a, a2, a3, … an-1 ; an = e }

Definition 2.2: Abelian (commutative) Group G is Abelian if a b = b a  a,b  G Common notations: • → + e → 0 Definition 2.3: Order Order g of group G = Number of elements in G Example 4: Dihedral group D2 Simplest non-cyclic group is D2 = { e, a = a–1, b = b–1, c = a b } ( Abelian, order = 4 ) Realizations: D2 = { symmetries of a rectangle } = { E , C2, σx, σy } = { E, C2 , C2', C2" }

2.2 Further Examples, Subgroups The simplest non-Abelian group is of order 6. { e, a, b = a–1, c = c–1, d = d–1, f = f–1 } Aliases: Dihedral group D3, C3v, or permutation group S3. Symmetries of an equilateral triangle: C3v = { E, C3, C32, σ1, σ2, σ3 } D3 = { E, C3, C32, C2', C2'', C2''' }

S3 = { e, (123), (132), (23), (13), (12) } (…) = cyclic permutations Tung's notation

Definition 2.4: Subgroup { H  G, • } is a subgroup of { G , • } . Example 1: D2 = { e, a, b, c } 3 subgroups: { e, a }, { e, b } , { e, c } Example 2: D3S3  { e, a, b = a–1, c = c–1, d = d–1, f = f–1 } 4 subgroups: { e, a, b } , { e, c }, { e, d }, { e, f } Infinite Group : Group order =  E.g. Td = { T(n) | nZ } Some subgroups: Continuous Group: Elements specified by continuous parameters E.g. Continuous translations T Continuous rotations R(2), R(3) Continuous translations & rotations E(2), E(3)

Crystallographic Point Groups: Cn, Cnv, Cnh, Dn, Dnv, Dnh, Dnd, Sn, T, Td, Th, ( Tetrahedral ) O, Oh, ( Cubic ) I ( icosahedral ) n = 2,3,4,6 v: vertical  h: horizontal  Dn: Cn with C2  Cn d: vert  between 2 C2 's Sn: Cn with i

Matrix / Classical groups: • General linear group GL(n) • Unitary group U(n) • Special Unitary group SU(n) • Orthogonal group O(n) • Special Orthogonal group SO(n)

2.3. The Rearrangement Lemma & the Symmetric Group Lemma: Rearrangement p b = p c → b = c where p, b, c  G Proof: p–1 both sides Corollary: p G = G rearranged; likewise G p Permutation: pi i ( Active point of view ) Product: p q = ( pk k) ( qi i ) (Rearranged)

Identity: Inverse: i  pi Symmetric (Permutation) groupSn { n! permutations of n objects } n-Cycle = ( p1, p2, p3,…, pn ) Every permutation can be written as a product of cycles

Definition 2.5: Isomorphism 2 groups G & G ' are isomorphic ( G G ' ) , if  a 1-1 onto mapping : G → G ' gi  gi'  gi gj = gk  gi gj' = gk' • Examples: • Rotational group Cn cyclic group Cn • D3  C3v S3 Theorem 2.1: Cayley Every group of finite order n is isomorphic to a subgroup of Sn Proof: Let G = { g1, g2, …, gn } . The required mapping is where : G → Sn 

Example 1: C3= { e, a, b = a2 ; a3=e } = { g1, g2, g3 } C3 { e, (123), (321) }, subgroup of S3 Example 2: D2= { e, a = a–1, b = b–1, c = a b } D2 { e, (12)(34), (13)(24), (14)(23) }, subgroup of S4

Example 3: C4= { e = a4, a, a2, a3 } D2 { e, (1234), (13)(24), (1432) }, subgroup of S4 • Let S be a subgroup of Sn that is isomorphic to a group G of order n. Then • The only element in S that contains 1-cycles is e ( else, rearrangement therem is violated ) • All cycles in a given element are of the same length ( else, some power of it will contain 1-cycles ) • E.g., [ (12)(345) ]2 = (1) (2) (345)2 • If order of G is prime, then S can contain only full n-cycles, ie, S is cyclic Theorem 2.2: A group of prime order is isomorphic to Cn Only 1 group for each prime order

2.4. Classes and Invariant Subgroups Definition 2.6: Conjugate Elements Let a , b  G. b is conjugate to a, or b~a, if  pG  b = p a p–1 • Example: S3 • (12) ~ (31) since (23) (31) (23)–1 = (23) (132) = (12)(3) = (12) • (123) ~ (321) since (12) (321) (12) = (12) (1)(23) = (123) Exercise: Show that for p, q  Sn , Hint:

Def: ~ is an equivalence relationif • a ~ a (reflexive) • a~b  b~a  (symmetric) • a~b, b~c  a~c (transitive) Conjugacy is an equivalence relation Proof : (reflexive) (symmetric)   (transitive)

An equivalence relation partitions (classifies members of) a set. Definition 2.7: Conjugate Class Let a  G, the conjugate class of a is the set ξ = { p a p–1 | p  G } • Comments: • Members of a class are equivalent & mutually conjugate • Every group element belongs to 1 & only 1 class • e is always a class by itself • For matrix groups, conjugacy = similarity transform

Example 1: S3 (3 classes): • ξ1 = { e } identity • ξ2 = { (12), (23), (31) } 2-cycles • ξ3 = { (123), (321) } 3-cycles  Permutations with the same cycle structure belong to the same class. Example 2: R(3) (Infinitely many classes): Let Ru(ψ) be a rotation about u by angle ψ. u = unit vector • Class: ξ(ψ) = { Ru(ψ) ; all u } = { All rotations of angle ψ } Example 3: E3(Infinitely many classes): Let Tu(b) be a translation along u by distance b. • Class: ξ(b) = { Tu(b) ; all u } = { All translations of distance b }

Def: Conjugate Subgroup Let H be a subgroup of G & a  G. H' = { a h a–1 | h  H } = Subgroupconjugate to H • Exercise: • Show that H' is a subgroup of G • Show that either H  H' or H  H' = e Definition 2.8: Invariant Subgroup H is an invariant subgroup of G if it is identical to all its conjugate subgroups. i.e., H = { a h a–1 | h  H }  a  G • Examples: • { e, a2 } is an invariant subgroup of C4 = { e = a4, a, a2, a3 } • { e, (123), (321) } is an invariant subgroup of S3 but { e, (12) } isn't • Tdm is an invariant subgroup of Td

Comments: • An invariant subgroup must consist of entire classes • Every group G has 2 trivial invariant subgroups {e} & G • Existence of non-trivial invariant subgroup  G can be factorized Definition 2.9: Simple & Semi-Simple Groups A group is simple if it has no non-trivial invariant subgroup. A group is semi-simple if it has no Abelian invariant subgroup. • Examples: • Cn with n prime are simple. • Cn with n non-prime are neither simple nor semi-simple. • n = p q  { e, Cp, C2p, …, C(q–1) p } is an Abelian invariant subgroup • S3 is neither simple nor semi-simple. { e, (123), (321) } is spoiler. • SO(3) is simple but SO(2) is not. Spoilers: Cn

2.5 Cosets and Factor (Quotient) Groups Definition 2.10: Cosets Let H = { h1, h2, … } be a subgroup of G & p G –H. Then p H = { p h1, p h2, … } is a left coset of H, & H p = { h1 p, h2 p, … } is a right coset of H. • Neither p H, nor H p, is a subgroup of G (no e) • All cosets of H have the same order as H ( rearrangement theorem) Lemma: Either p H = q H or p H  q H =  • Proof: • If  hi & hj p hi = q hj  p = q hj hi–1 = q hk  qH • p H = q hk H= q H Negation of above gives 2nd part of lemma. Corollary: G is partitioned by cosets of H.  Lagrange theorem

Theorem 2.3: Lagrange ( for finite groups ) H is a subgroup of G  Order(G) / Order(H) = nG / nH N • Examples: S3 • H1 = { e, (123), (321) }. One coset: • M = (12) H1 = (23) H1 = (31) H1 • = { (12), (23), (31) } • H2 = { e, (12) } . Two cosets: • M1 = (23) H2 = (321) H2 = { (23), (321) } • M2 = (31) H2 = (123) H2 = { (31), (123) }

Thm: H is an invariant subgroup  pH = Hp Proof: H invariant  pHp–1 = H Theorem 2.4: Factor / Quotient Group G/H Let H be an invariant subgroup of G. Then G/H  { { pH | p G }, • } with pH • qH  (pq) H is a (factor) group of G. Its order is nG / nH. Example1: C4 = { e = a4, a, a2, a3 } H = { e, a2 } is an invariant subgroup. Coset M = a H = a2 H = { a, a3 }. Factor group C4/H = { H, M }  C2

Example2: S3 = { e, (123), (132), (23), (13), (12) } H = { e, (123), (132) } is invariant Coset M = { (23), (13), (12) } Factor group S3 /H = { H, M }  C2 C3v / C3 C2 Example3: Td  = { T(n), n Z } m = { T(mn), n Z } is an invariant subgroup. Cosets: T(k) m k = 1, …, m –1 & T(m) m = m Products: T(k) m • T(j) m = T(k+j) m Factor group: / m = { { T(k) m | k = 1, …, m –1 }, • }  Cm Caution: m   Example 4: E3 H = T(3) is invariant. E3 / T(3)  R(3)

2.6 Homomorphisms Definition 2.11: Homomorphism G is homomorphic to G' ( G ~ G' ) if  a group structure preserving mapping from G to G', i.e.  : G  G' g  g' = (g)  a b = c  a' b' = c' Isomomorphism:  is invertible ( 1-1 onto ). Example: : S3 C2 with (e) = [(123)] = [(321)] = e [(23)] = [(31)] = [(12)] = a is a homorphism S3~ C2.

Theorem 2.5: Let : G  G' be a homomorphism and Kernel = K = { g | (g) = e' } Then K is an invariant subgroup of G and G/K  G' Proof1 ( K is a subgroup of G ):  is a homomorphism:  a, b  K  (ab) = (a) (b) = e' e' = e'  ab  K (closure) (ae) = (a) (e) = e' (e) = (e) = (a) = e'  (e) = e'  e  K (identity) (a–1a) = (a–1 ) ( a) = (a–1 ) e' = (a–1 ) = (e) = e'  a–1  K (inverse) Associativity is automatic. QED

Proof 2 ( K is a invariant ): Let a  K & g  G. ( g a g–1 ) = (g) (a) ( g–1) = (g) ( g–1) = (g g–1) = (e) = e'  g a g–1  K Proof3 ( G/K  G' ): G/K = { pK | p G}  ( pa ) = ( p ) ( a ) = ( p ) e' = ( p )  a  K i.e.,   maps the entire coset pK to one element ( p ) in G'. Hence,  : G/K  G' with ( pK ) = ( p ) = ( q pK ) is 1-1 onto. ( pK qK ) = [ (pq)K ] = ( pq ) = ( p) ( q) = ( pK) (qK )   is a homomorphism. QED

Kernel G/K  G'

2.7 Direct Products • Definition 2.12: Direct Product Group A  B • Let A & B be subgroups of group G such that • a b = b a  a  A & b  B •  g  G,  a  A & b  B g = a b = b a • Then G is the direct product of A & B, i.e, G = A  B = B  A • Example 1: C6 = { e = a6, a, a2, a3, a4, a5 } • Let A = { e, a3 } & B = { e, a2, a4 } • a b = b a trivial since C6 is Abelian • e = e e, a = a3 a4, a2 = e a2, a3 = a3 e, a4 = e a4, a5 = a3 a2 •  C6 = A  B  C2  C3

Example 2: O(3) = R(3)  { e, IS } • Thm: • G = A  B  • A & B are invariant subgroups of G • G/A  B, G/B  A • Proof: • g = a b  g a' g–1 = a b a' b–1 a–1 = a a' b b–1 a–1 = a a' a–1  A • A is invariant ; dido B. G = { a B | a  A }  G/B  A & similarly for B Caution: G/B  A  does not imply G = A  B Example: S3 H = { e, {123}, {321} } is invariant. Let Hi = { e, (j k) } ( i,j,k cyclic ) Then S3/H  Hi but S3 H  Hi

• More by User

Lecture 2 Outline of basic theory

Lecture 2 Outline of basic theory. defecation. feeding. food. faeces. assimilation. reserve. somatic maintenance. maturity maintenance. . 1- . maturation reproduction. growth. maturity offspring. structure. Standard DEB model. Topological alternatives 11.1c.

589 views • 41 slides

Basic Electron Theory

Basic Electron Theory. Basic Electron Theory. This presentation will Review the basic structure of the atom. Define conductor, insulator, and semiconductor. Structure of an Atom. Example – Carbon Atom. Nucleus 6 Protons 6 Neutrons. Electrons. +. +. +. +. +. +. -. -. -. -. -.

1.74k views • 10 slides

Lecture 2: Basic Information Theory

TSBK01 Image Coding and Data Compression. Lecture 2: Basic Information Theory. Jörgen Ahlberg Div. of Sensor Technology Swedish Defence Research Agency (FOI). Today. What is information theory about? Stochastic (information) sources. Information and entropy. Entropy for stochastic sources.

901 views • 31 slides

Group THeory

Group THeory. Bingo. You must write the slide number on the clue to get credit. Rules and Rewards. The following slides have clues Each clue may refer to a theorem or term on your bingo card If you believe it does, write the slide number in the corresponding box

549 views • 32 slides

Basic Optimization Theory

Basic Optimization Theory. LP (Linear Programming) NLP (Non-Linear Programming) IP (Integer Programming) MIP (Mixed Integer Programming) MINLP (Mixed Integer Non-Linear Programming). Types Of Optimization. Parameter Optimization Configuration Optimization

907 views • 26 slides

Lecture 2 Basic Number Theory and Algebra

Lecture 2 Basic Number Theory and Algebra.

640 views • 51 slides

Group theory

Group theory. 1st postulate - combination of any 2 elements, including an element w/ itself, is a member of the group. 2nd postulate - the set of elements of the group contains the identity element (IA = A)

729 views • 28 slides

Group Theory

Group Theory. T.Inui, Y.Tanabe, Y.Onodera Group Theory &amp; Its Applications in Physics, Springer Verlag (90). Symmetry &amp; Role of Group Theory Groups Vector Spaces Group Representation I Group Representation II Group Representation in Quantum Mehanics Rotation Group

974 views • 3 slides

Theme Group 2- Theory

Theme Group 2- Theory. Elementary Particle Physics, Gravitation Theory and Theoretical Quarks, Hadrons and Nuclei. Theme Group 2 -Theory. Elementary Particles (7 faculty, 2 post docs, 10 students, NSF,DOE ) Supersymmetry, Supergravity and Grand Unification

579 views • 35 slides

Basic Computer Theory

Basic Computer Theory. BTA3OI (To be used with handout). Computer Theory. In order to make good decisions about what computer equipment will best suit your needs for your business, you will need to know about hardware and software.

1.44k views • 13 slides

Basic Theory

Basic Theory. Matter was created Stars were an error. Protoplanet Hypothesis. 5 billion years ago a clod of dust and gas 10 billion km in diameter rotated. As time passed the cloud shrank under its own gravity, or collapsed from an explosion.

384 views • 10 slides

Basic Control Theory

Basic Control Theory. State of the system:. Plant equation:. Motor error.

146 views • 4 slides

Basic Group Accounts – F2 Part 2

Basic Group Accounts – F2 Part 2. Management Level – Paper F2 Advanced Financial Reporting. Lecture - 023. Vidya Rajawasam ACMA CGMA MBA. Basic Group Accounts – F2. We have discussed the subject area related Basic Group Accounts – F2 , Fair Values and Good will

462 views • 45 slides

477 views • 31 slides

386 views • 35 slides

Group theory. C 2 1 C 2 m 1 m 1 1 C 2 1 1 m C 2 C 2 1 m m 1. Isomorphism: Two groups isomorphic if they have same type of multiplication table.

245 views • 17 slides

Group theory. Group Definition. A group is a set G = {E,  } where E is a set of elements and  is a binary operation on E. For a group we have the following axioms:. Closed under binary operation Asso c iative binary operation Identity element Inverse element. A_001 A_002 A_003

372 views • 16 slides

Basic circuit theory

Sensors Technology – MED4. Basic circuit theory. Lecturer: Smilen Dimitrov. Introduction. The model that we introduced for ST. Introduction. We have discussed The units of voltage, current and resistance, in terms of electric circuits The definition of an elementary electric circuit

391 views • 26 slides

669 views • 28 slides

485 views • 42 slides

Stack Exchange Network

Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

Q&A for work

Connect and share knowledge within a single location that is structured and easy to search.

Presentation of subgroup

Let $G$ be the group with presentation $$G = \langle \sigma_1 ,\sigma _2 , \sigma _3\, |\, \sigma _1^2=\sigma _2^2=\sigma _3^2=(\sigma _1\sigma _2)^p =(\sigma _2\sigma _3)^q =(\sigma _3\sigma _1)^r =1\rangle .$$ I want to have a presentation for the subgroup $H$ generated by the elements $\tau _1=\sigma _1\sigma _2,\, \tau _2=\sigma _2\sigma _3,\ \tau _3=\sigma _3\sigma _1$ .

Is it enough to conjecture the presentation $$ H=\langle \tau _1,\tau _2 ,\tau _3\, |\, \tau _1^p=\tau _2^q=\tau _3^r=\tau _1\tau _2\tau _3 =1 \rangle$$ and argue that the relations in the presentation of $G$ clearly imply the ones conjectured for $H$ and that the relations of $H$ imply the relations in the presentation of $G$ .

• group-theory
• solution-verification
• group-presentation
• combinatorial-group-theory

• $\begingroup$ The group is a triangle group . I don't know whether this helps or not though. $\endgroup$ –  Shaun Commented Oct 27, 2020 at 18:50
• 3 $\begingroup$ No, this is not sufficient, as there may be "hidden" relations. Either you need to do more work (expand on your word "clearly"), or you can use Reidemeister-Schreier (Google it, or search this site), which gives a process to find a presentation of a given subgroup of a group. It works nicely here because $H$ has finite index in $G$. $\endgroup$ –  user1729 Commented Oct 27, 2020 at 19:02
• 2 $\begingroup$ But in fact the conjectured presentation of $H$ is correct - you just need to prove it. $\endgroup$ –  Derek Holt Commented Oct 27, 2020 at 19:46
• 1 $\begingroup$ Thanks a lot. I looked up the Reidemeister-Schreier method and got the presentation. $\endgroup$ –  user744043 Commented Oct 27, 2020 at 22:50

No, this is not sufficient, as there may be "hidden" relations. In your example, $H$ does indeed have the given presentation, and it is presumably possible to show this "by hand" using properties of the group $G$ , but it is not "clearly" true.

Alternatively, you can use the Reidemeister-Schreier method. This is a process to find a presentation of a given subgroup of a group, and it works nicely here because $H$ has finite index in $G$ . There are two approaches to the method: the classical combinatorial/algebraic version as covered in Section 2.3 of the book Combinatorial group theory by Magnus, Karrass and Solitar, or in Section II.4 of Lyndon and Schupp's book of the same name, and the topological version using coverings of presentation complexes (see here ). Personally, I favour the topological version, as I view it as a "visualisation" of the algebraic version.

The process can also be done on a computer (see here ), although the computer will want $p,q,r$ to be fixed.

You must log in to answer this question.

Not the answer you're looking for browse other questions tagged group-theory solution-verification group-presentation combinatorial-group-theory ..

• Featured on Meta
• We spent a sprint addressing your requests — here’s how it went
• Upcoming initiatives on Stack Overflow and across the Stack Exchange network...

Hot Network Questions

• Accommodating whiteboard glare for low-vision student
• Whom did Rashi call "oker harim"
• What enforcement exists for medical informed consent?
• Could a Black Market exist in a cashless society (digital currency)?
• French Election 2024 - seat share based on first round only
• Power pedals on a fully MTB (riding flat roads), later on road/gravel bike
• Which Präposition should I use with Erwartungen?
• Can I exit România on a different passport than the one used for entering the country?
• Part name of this IC - Analog Devices, 8-pin, "S 6B" A 06" "C 42"
• Help understanding the implications of Security Breach section of an NDA
• Can IBM Quantum hardware handle any CSWAP at all?
• Pattern on a PCB
• Algebraic and continuous duals of an inverse limit of finite dimensional vector spaces
• Mechanism behind a pink human skeleton
• Are there countries where only voters affected by a given policy get to vote on it?
• Switching Tenure-Track Positions Within Same University
• Weak copyleft LGPL-like license for static linking
• Does physical reality exist without an observer?
• Irrigation system vs weed prevention
• What does "master o' the Tiger" mean?
• Does the damage from Thunderwave occur before or after the target is moved
• To be considered airworthy, are commercial aircraft fuselages required to support some amount of external overpressure without buckling?
• Unable to use split. tryed doing with align got more error in that also due to this im unable to fit the equation the page
• Is it an option for the ls utility specified in POSIX.1-2017?

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

How to Make a “Good” Presentation “Great”

• Guy Kawasaki

Remember: Less is more.

A strong presentation is so much more than information pasted onto a series of slides with fancy backgrounds. Whether you’re pitching an idea, reporting market research, or sharing something else, a great presentation can give you a competitive advantage, and be a powerful tool when aiming to persuade, educate, or inspire others. Here are some unique elements that make a presentation stand out.

• Fonts: Sans Serif fonts such as Helvetica or Arial are preferred for their clean lines, which make them easy to digest at various sizes and distances. Limit the number of font styles to two: one for headings and another for body text, to avoid visual confusion or distractions.
• Colors: Colors can evoke emotions and highlight critical points, but their overuse can lead to a cluttered and confusing presentation. A limited palette of two to three main colors, complemented by a simple background, can help you draw attention to key elements without overwhelming the audience.
• Pictures: Pictures can communicate complex ideas quickly and memorably but choosing the right images is key. Images or pictures should be big (perhaps 20-25% of the page), bold, and have a clear purpose that complements the slide’s text.
• Layout: Don’t overcrowd your slides with too much information. When in doubt, adhere to the principle of simplicity, and aim for a clean and uncluttered layout with plenty of white space around text and images. Think phrases and bullets, not sentences.

As an intern or early career professional, chances are that you’ll be tasked with making or giving a presentation in the near future. Whether you’re pitching an idea, reporting market research, or sharing something else, a great presentation can give you a competitive advantage, and be a powerful tool when aiming to persuade, educate, or inspire others.

• Guy Kawasaki is the chief evangelist at Canva and was the former chief evangelist at Apple. Guy is the author of 16 books including Think Remarkable : 9 Paths to Transform Your Life and Make a Difference.

Partner Center