null hypothesis ks test

• It only applies to continuous distributions.
• It tends to be more sensitive near the center of the distribution than at the tails.
• Perhaps the most serious limitation is that the distribution must be fully specified. That is, if location, scale, and shape parameters are estimated from the data, the critical region of the K-S test is no longer valid. It typically must be determined by simulation.

Dataaspirant

• Beginners Guide
• Data science courses

Kolmogorov-Smirnov Test [KS Test]: When and Where to Use

The Kolmogorov-Smirnov test is a statistical method used to assess the similarity between two probability distributions. It is a non-parametric test, meaning that it makes no assumptions about the underlying distribution of the data.

The Kolmogorov-Smirnov test is based on the maximum difference between the cumulative distribution functions (CDFs) of the two distributions being compared. The test statistic, known as the D statistic , measures this difference and is used to determine whether the two distributions are significantly different from each other.

The Kolmogorov-Smirnov test has a wide range of applications, from comparing the performance of two different machine learning models to testing for normality in a dataset. It is also commonly used in goodness-of-fit tests, where it is used to compare the distribution of a sample to a theoretical distribution .

Kolmogorov-Smirnov Test [KS Test]: What, When and Where to Use

In this article, we will provide a comprehensive introduction to the Kolmogorov-Smirnov test, including its mathematical basis, how it works, and its strengths and weaknesses. We will also discuss practical applications of the test, including how it can be used in machine learning and statistical analysis.

Whether you are a data scientist looking to expand your statistical toolkit or a beginner seeking an introduction to hypothesis testing, this guide will provide you with the knowledge and skills to effectively use the Kolmogorov-Smirnov test in your work.

What is Kolmogorov-Smirnov Test ?

The Kolmogorov-Smirnov test, also known as the KS test, is a powerful statistical method used to compare two probability distributions. It was first introduced in the early 1930s by Andrey Kolmogorov and Nikolai Smirnov , two prominent Russian mathematicians. 

Since then, it has become a widely used technique in statistical analysis and data science .

Overview of the Kolmogorov-Smirnov test

The KS test measures the maximum distance between the cumulative distribution functions (CDFs) of two samples being compared, and is sensitive to differences in both location and shape. 

It is a non-parametric method, meaning that it makes no assumptions about the underlying distribution of the data being compared. This makes it particularly useful in situations where the distribution is unknown or cannot be easily modeled, such as in machine learning applications .

The KS test has numerous uses in both academic and industrial research. In academic settings, it is frequently employed in hypothesis testing to ascertain whether two samples are drawn from the same distribution. In tests to determine how well a sample fits a theoretical distribution, it is also utilized. 

The KS test is especially helpful in data science applications in the workplace because it can be used to compare the effectiveness of various machine learning models .

Data scientists can identify the best model for a given task by comparing the distribution of predicted values from various models.

Mathematical Basis Of Kolmogorov-Smirnov Test

The Kolmogorov-Smirnov test is a statistical method used to compare two probability distributions. It is based on the maximum difference between the cumulative distribution functions (CDFs) of two samples being compared. 

The test statistic measures the largest vertical distance between the two CDFs. The larger the test statistic, the greater the difference between the two distributions being compared.

Definition of the KS Test Statistic

The test statistic used in the KS test is denoted by D and is defined as the maximum difference between the empirical distribution function (EDF) of the two samples being compared. 

The EDF is a step function that assigns a probability of 1/n to each observation in the sample, where n is the sample size. The EDF is constructed by ordering the observations in each sample and plotting the cumulative probability of each observation.

Calculation of the KS Test Statistic

The test statistic is calculated by finding the largest vertical distance between the EDFs of the two samples being compared. This can be done by subtracting the values of the two EDFs at each observation point and taking the absolute value of the difference. 

The test statistic D is then the maximum absolute difference between the two EDFs.

The KS test statistic is given by:

Dn = max|Fn1(x) - Fn2(x)|

where Fn1 and Fn2 are the empirical CDFs of the two samples, and x is a point in the support of the data. The test statistic Dn is a measure of the maximum difference between the two CDFs.

Interpretation of the test statistic

To ascertain whether two samples originate from the same underlying distribution, the KS test is frequently used in hypothesis testing. The alternative hypothesis is that the two samples were taken from different populations, while the null hypothesis states that they were taken from the same population. 

When comparing a calculated value with a critical value taken from a table or computed using the significance level and sample size, the KS test statistic is used.

The null hypothesis is rejected and it can be inferred that the two samples come from different populations if the calculated value is greater than the critical value. 

If not, the null hypothesis is not disproven. The probability of rejecting the null hypothesis when it is true depends on the significance level.

Hypothesis Testing

Hypothesis testing is a statistical method used to determine whether an observed effect is statistically significant. In the context of the Kolmogorov-Smirnov test.

The null hypothesis is that the two samples being compared are drawn from the same underlying probability distribution , while the alternative hypothesis is that they are drawn from different distributions. 

The goal of hypothesis testing is to determine whether there is enough evidence to reject the null hypothesis and support the alternative hypothesis.

Null and alternative hypotheses

The underlying premise of the null hypothesis is that there is no discernible difference between the two samples under comparison. The opposite of the null hypothesis, the alternative hypothesis postulates that the two samples were taken from various underlying distributions. 

In the KS test, the alternative hypothesis is that the two samples come from different distributions, while the null hypothesis is that they both come from the same underlying distribution.

Significance level and p-values

The significance level is the probability of rejecting the null hypothesis when it is true. It is typically denoted by alpha and is set by the experimenter before the test is conducted. The p-value is a measure of the evidence against the null hypothesis provided by the data. 

It is the probability of observing a test statistic as extreme or more extreme than the one calculated from the data, assuming that the null hypothesis is true.

If the p-value is less than the significance level, then the null hypothesis is rejected in favor of the alternative hypothesis.

Rejection and acceptance of the null hypothesis

The decision to reject or accept the null hypothesis is based on the calculated test statistic and the p-value. If the test statistic exceeds the critical value from the table or the p-value is less than the significance level, then the null hypothesis is rejected in favor of the alternative hypothesis. 

If the test statistic does not exceed the critical value or the p-value is greater than the significance level, then the null hypothesis is not rejected.

The decision to reject or accept the null hypothesis depends on the experimenter's chosen significance level, the size of the samples being compared, and the test statistic calculated from the data.

Types of Kolmogorov-Smirnov Tests

The Kolmogorov-Smirnov test has several variants, each with a different purpose. 

One-sample test

Two-sample test.

• Goodness-of-fit test 

The one-sample test is used to test whether a sample comes from a specific distribution, while the two-sample test is used to test whether two samples come from the same distribution. 

The goodness-of-fit test is used to test whether a sample comes from a specified distribution or a theoretical distribution.

The one-sample KS test is used to test whether a sample comes from a specific probability distribution. The null hypothesis is that the sample comes from the specified distribution.

The test statistic is the maximum absolute difference between the empirical distribution function of the sample and the cumulative distribution function of the specified distribution. 

The critical value of the test statistic is obtained from a table or calculated using a formula based on the sample size and the chosen significance level.

• Test statistic: 0.12150323555369263
• P-value: 0.09594399636962193

The two-sample KS test is used to test whether two samples come from the same probability distribution. The null hypothesis is that the two samples come from the same distribution.

The test statistic is the maximum absolute difference between the empirical distribution functions of the two samples. 

The critical value of the test statistic is obtained from a table or calculated using a formula based on the sample sizes and the chosen significance level.

• Test statistic: 0.26
• P-value: 0.002219935934558366

Goodness-of-fit test

The goodness-of-fit KS test is used to test whether a sample comes from a specified distribution or a theoretical distribution. The null hypothesis is that the sample comes from the specified distribution. 

The test statistic is the maximum absolute difference between the empirical distribution function of the sample and the cumulative distribution function of the specified distribution.

• Test statistic: 0.07211687480182327
• P-value: 0.6489328604867581

Advantages and Limitations Of Kolmogorov-Smirnov Test

The Kolmogorov-Smirnov (KS) test is a widely used statistical test that can be applied to a variety of problems in science, engineering, and other fields.

The KS test is known for its ability to compare two sets of data and determine if they are drawn from the same distribution or not. As with any statistical method, the KS test has its advantages and limitations. 

The Kolmogorov-Smirnov test has several advantages that make it a useful tool in statistical analysis:

• Non-parametric: The Kolmogorov-Smirnov test is a non-parametric test, which means that it does not assume any specific distribution for the data. This makes it a versatile test that can be used in a wide range of applications.
• Easy to implement: The Kolmogorov-Smirnov test is easy to implement and can be done using simple statistical software. It does not require any specialized knowledge or expertise.
• Suitable for small sample sizes: The Kolmogorov-Smirnov test can be used with small sample sizes, making it useful in situations where data is limited .

Despite its advantages, the Kolmogorov-Smirnov test also has some limitations:

• Sensitive to sample size: The power of the test is affected by the sample size. As the sample size increases, the test becomes more powerful.
• Sensitive to outliers: The test is sensitive to outliers in the data, which can result in incorrect rejection of the null hypothesis.
• Limited to continuous distributions: The Kolmogorov-Smirnov test is limited to continuous distributions and cannot be used for discrete or categorical data.

Applications of the Kolmogorov-Smirnov Test

The Kolmogorov-Smirnov (K-S) test is a versatile statistical method that has found its place in a variety of fields, lending its power to assess the compatibility between different data distributions . Its nonparametric nature and adaptability have contributed to its widespread use in diverse sectors.

Here's a deeper dive into the realms where the K-S test has been making significant contributions:

1. Machine Learning:

The K-S test assists in assessing the performance of machine learning models by measuring the deviation between the predicted output and the actual results. This quantification can provide critical insights into the model's behavior.

By understanding how closely the predicted results align with actual outcomes, data scientists and machine learning engineers can make the necessary tweaks to enhance the accuracy and reliability of their models.

2. Statistical Analysis:

The K-S test comes to the rescue by allowing analysts to make this determination. Especially when faced with data that doesn't follow the conventional bell-curve or the normal distribution, the K-S test's nonparametric approach provides a reliable tool to make such comparisons, helping in deducing meaningful conclusions from the data.

3. Goodness-of-Fit Tests:

The K-S test serves as an excellent goodness-of-fit test. Researchers and analysts use it to ascertain if their sample data adheres to a hypothesized distribution.

Such determinations are crucial in various sectors, ranging from finance—where understanding distribution is key for risk management—to biology, where patterns of data can provide insights into phenomena, and engineering, where data consistency can be critical for process optimizations.

In all these applications, the Kolmogorov-Smirnov test stands out due to its simplicity and robustness, providing reliable results without the need for stringent assumptions about the nature of the data.

How to Conduct a Kolmogorov-Smirnov Test

The Kolmogorov-Smirnov test is a statistical test used to determine if a sample follows a specific distribution or if two samples come from the same population.

Conducting the test involves several steps, and it is important to follow them carefully to ensure accurate results.

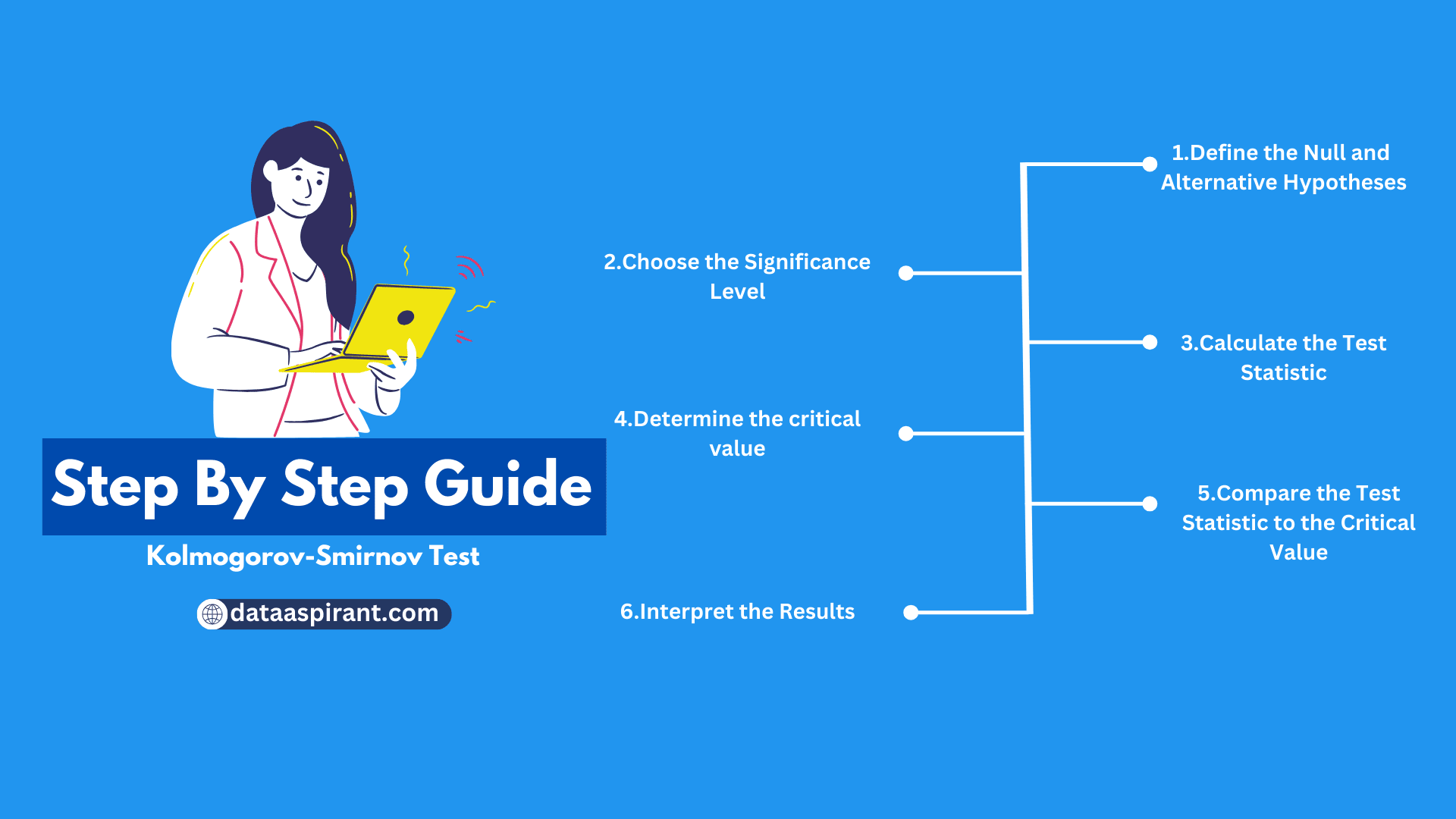
Kolmogorov-Smirnov Test Step-by-step Guide

1. define the null and alternative hypotheses:.

• The null hypothesis states that the sample follows a specific distribution or that two samples come from the same population.
• The alternative hypothesis states that the sample does not follow the specific distribution or that two samples do not come from the same population.

2. Choose the significance level:

• The significance level (alpha) is the probability of rejecting the null hypothesis when it is actually true.
• A common significance level is 0.05, which means there is a 5% chance of rejecting the null hypothesis when it is true.

3. Calculate the test statistic:

• The test statistic is calculated based on the difference between the empirical distribution function (EDF) of the sample(s) and the theoretical distribution function.
• The formula for the test statistic varies depending on the type of Kolmogorov-Smirnov test being conducted.

4. Determine the critical value:

• The critical value is the value at which the null hypothesis can be rejected.
• The critical value is determined based on the significance level and the sample size.

5. Compare the test statistic to the critical value:

• If the test statistic is greater than the critical value, the null hypothesis can be rejected.
• If the test statistic is less than or equal to the critical value, the null hypothesis cannot be rejected.

6. Interpret the results:

• If the null hypothesis is rejected, it means that the sample does not follow the specific distribution or that the two samples do not come from the same population.
• If the null hypothesis is not rejected, it means that there is not enough evidence to conclude that the sample does not follow the specific distribution or that the two samples do not come from the same population.

Kolmogorov-Smirnov Test Implementation In Python

Here is a example of using the  Kolmogorov-Smirnov Test

Kolmogorov-Smirnov test results:

• Statistic: 0.430
• P-value: 0.000

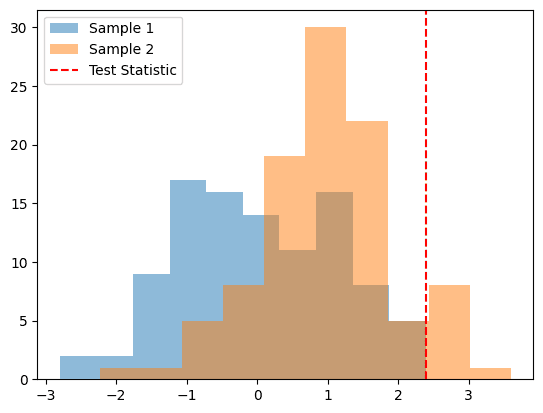
In this example, we generate two random samples using NumPy's normal function, with means of 0 and 1 and standard deviations of 1. We then compute the test statistic and p-value using ks_2samp from the SciPy library, and print the results.

Finally, we visualize the two samples using a histogram, with the test statistic represented as a vertical dashed line. The alpha parameter controls the transparency of the bars, and the label parameter adds a legend to the plot. The axvline function adds a vertical line to the plot at the location of the test statistic.

The Kolmogorov-Smirnov test is a powerful statistical tool that is widely used in many fields, including machine learning , statistical analysis, and goodness-of-fit tests. It allows researchers to determine whether a set of data follows a specific distribution, which is essential in many scientific and business applications.

In this comprehensive guide, we have covered the mathematical basis of the Kolmogorov-Smirnov test, its different types, advantages, and limitations. We have also provided a step-by-step guide on how to conduct the test and included code examples to help you get started.

Despite its wide use, the Kolmogorov-Smirnov test has some limitations, such as its sensitivity to sample size and its inability to handle censored data . Therefore, future research could focus on developing new and more robust statistical tests that overcome these limitations.

Additionally, the application of the Kolmogorov-Smirnov test in machine learning and big data analytics is an area of active research. Researchers are exploring ways to integrate the test into more advanced algorithms to improve model performance and reduce the need for labeled data.

Frequently Asked Questions (FAQs) On Kolmogorov-Smirnov (K-S) Test

1. what is the kolmogorov-smirnov (k-s) test.

The Kolmogorov-Smirnov Test is a nonparametric test used to compare the sample distribution with a reference probability distribution or to compare two sample distributions.

2. Is the K-S Test Parametric or Nonparametric?

The K-S test is nonparametric, meaning it doesn't assume a specific distribution for the data.

3. When Should I Use the K-S Test?

You can use the K-S test when you want to check if your data follows a specific distribution (e.g., normal, exponential) or when comparing two sets of data to see if they come from the same distribution.

4. How Does the K-S Test Work?

The test computes the maximum difference (D) between the cumulative distribution functions (CDF) of the sample data and the reference distribution or between the CDFs of two sample datasets.

5. What are the Key Assumptions of the K-S Test?

The main assumptions include that the data is continuous and that there are no ties if comparing two datasets.

6. How Do I Interpret the Results of a K-S Test?

If the p-value is below a significance level (e.g., 0.05), you reject the null hypothesis. This means the sample data doesn't follow the reference distribution or that the two samples have different distributions.

7. Can the K-S Test be Used for Categorical Data?

No, the K-S test is designed for continuous data. For categorical data, you might consider the Chi-squared test or other suitable tests.

8. Where is the K-S Test Commonly Used?

The test is widely used in fields like finance (e.g., to check model assumptions), ecology (e.g., comparing biodiversity between sites), and many scientific disciplines for distribution comparison.

9. Is the K-S Test Sensitive to the Sample Size?

Yes, with smaller sample sizes, the test might not be very powerful in detecting differences, while with larger samples, even minor deviations can be detected.

10. Are There Alternatives to the K-S Test?

Yes, other tests like the Anderson-Darling test, Shapiro-Wilk test, or Lilliefors test can also be used to check data normality or compare distributions.

11. What Limitations Should I be Aware of with the K-S Test?

The K-S test is sensitive to sample size, it's not suitable for categorical data, and it focuses on the largest deviation between CDFs which might not always capture the overall pattern.

Recommended Courses

Machine Learning Course

Rating: 4.5/5

Deep Learning Course

Rating: 4/5

FACEBOOK |  QUORA  | TWITTER |  GOOGLE+  |  LINKEDIN |  REDDIT   |  FLIPBOARD  |  MEDIUM  |  GITHUB

I hope you like this post. If you have any questions ? or want me to write an article on a specific topic? then feel free to comment below.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Awarded top 75 data science blog

Dataaspirant awarded top 75 data science blog

Unlimited access to 3k+ courses

Data Science Dojo

Recent Posts

• What to Do If Your Company Is Hit with Ransomware
• When Is the Right Time to Outsource a Dot Net Project?
• Predictive Analytics in Healthcare: How Data Science is Revolutionizing Early Detection and Legal Standards
• How to Leverage Data Science and AI Consulting Services for Your Business Success
• Optimizing Law Firm Profitability through Advanced Data Analysis Techniques

Build Your Career In AI With Andrew ng Deep learning courses

Andrew ng Deep learning courses

• Computer Vision
• Data Science
• Data Science Events
• Deep Learning
• Machine Learning
• Natural Language Processing
• Recommendation Engine
• Time Series

Quick Links

• Current Challenges in Computer Science: Addressing the Cybersecurity Skills Gap
• 10 Ways Technology Can Help You Attract and Retain Customers
• Challenges In Project Management: Common Issues Faced by Consulting Firms
• MATLAB Operators and Symbols: Types and Uses
• Boosting Your Networking: Data Science & Podcasting to the Rescue

© Copyright 2023 by dataaspirant.com . All rights reserved.

Session expired

Please log in again. The login page will open in a new tab. After logging in you can close it and return to this page.

• Statistics Tutorial
• Adjusted R-Squared
• Analysis of Variance
• Arithmetic Mean
• Arithmetic Median
• Arithmetic Mode
• Arithmetic Range
• Best Point Estimation
• Beta Distribution
• Binomial Distribution
• Black-Scholes model
• Central limit theorem
• Chebyshev's Theorem
• Chi-squared Distribution
• Chi Squared table
• Circular Permutation
• Cluster sampling
• Cohen's kappa coefficient
• Combination
• Combination with replacement
• Comparing plots
• Continuous Uniform Distribution
• Continuous Series Arithmetic Mean
• Continuous Series Arithmetic Median
• Continuous Series Arithmetic Mode
• Cumulative Frequency
• Co-efficient of Variation
• Correlation Co-efficient
• Cumulative plots
• Cumulative Poisson Distribution
• Data collection
• Data collection - Questionaire Designing
• Data collection - Observation
• Data collection - Case Study Method
• Data Patterns
• Deciles Statistics
• Discrete Series Arithmetic Mean
• Discrete Series Arithmetic Median
• Discrete Series Arithmetic Mode
• Exponential distribution
• F distribution
• F Test Table
• Frequency Distribution
• Gamma Distribution
• Geometric Mean
• Geometric Probability Distribution
• Goodness of Fit
• Gumbel Distribution
• Harmonic Mean
• Harmonic Number
• Harmonic Resonance Frequency
• Hypergeometric Distribution
• Hypothesis testing
• Individual Series Arithmetic Mean
• Individual Series Arithmetic Median
• Individual Series Arithmetic Mode
• Interval Estimation
• Inverse Gamma Distribution
• Kolmogorov Smirnov Test
• Laplace Distribution
• Linear regression
• Log Gamma Distribution
• Logistic Regression
• Mcnemar Test
• Mean Deviation
• Means Difference
• Multinomial Distribution
• Negative Binomial Distribution
• Normal Distribution
• Odd and Even Permutation
• One Proportion Z Test
• Outlier Function
• Permutation
• Permutation with Replacement
• Poisson Distribution
• Pooled Variance (r)
• Power Calculator
• Probability
• Probability Additive Theorem
• Probability Multiplecative Theorem
• Probability Bayes Theorem
• Probability Density Function
• Process Sigma
• Quadratic Regression Equation
• Qualitative Data Vs Quantitative Data
• Quartile Deviation
• Range Rule of Thumb
• Rayleigh Distribution
• Regression Intercept Confidence Interval
• Relative Standard Deviation
• Reliability Coefficient
• Required Sample Size
• Residual analysis
• Residual sum of squares
• Root Mean Square
• Sample planning
• Sampling methods
• Scatterplots
• Shannon Wiener Diversity Index
• Signal to Noise Ratio
• Simple random sampling
• Standard Deviation
• Standard Error ( SE )
• Standard normal table
• Statistical Significance
• Statistics Formulas
• Statistics Notation
• Stem and Leaf Plot
• Stratified sampling
• Student T Test
• Sum of Square
• T-Distribution Table
• Ti 83 Exponential Regression
• Transformations
• Trimmed Mean
• Type I & II Error
• Venn Diagram
• Weak Law of Large Numbers
• Statistics Useful Resources
• Statistics - Discussion
• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Statistics - Kolmogorov Smirnov Test

This test is used in situations where a comparison has to be made between an observed sample distribution and theoretical distribution.

K-S One Sample Test

This test is used as a test of goodness of fit and is ideal when the size of the sample is small. It compares the cumulative distribution function for a variable with a specified distribution. The null hypothesis assumes no difference between the observed and theoretical distribution and the value of test statistic 'D' is calculated as:

$D = Maximum |F_o(X)-F_r(X)|$

Where −

${F_o(X)}$ = Observed cumulative frequency distribution of a random sample of n observations.

and ${F_o(X) = \frac{k}{n}}$ = (No.of observations ≤ X)/(Total no.of observations).

${F_r(X)}$ = The theoretical frequency distribution.

The critical value of ${D}$ is found from the K-S table values for one sample test.

Acceptance Criteria: If calculated value is less than critical value accept null hypothesis.

Rejection Criteria: If calculated value is greater than table value reject null hypothesis.

Problem Statement:

In a study done from various streams of a college 60 students, with equal number of students drawn from each stream, are we interviewed and their intention to join the Drama Club of college was noted.

It was expected that 12 students from each class would join the Drama Club. Using the K-S test to find if there is any difference among student classes with regard to their intention of joining the Drama Club.

${H_o}$: There is no difference among students of different streams with respect to their intention of joining the drama club.

We develop the cumulative frequencies for observed and theoretical distributions.

Test statistic ${|D|}$ is calculated as:

The table value of D at 5% significance level is given by

Since the calculated value is greater than the critical value, hence we reject the null hypothesis and conclude that there is a difference among students of different streams in their intention of joining the Club.

K-S Two Sample Test

When instead of one, there are two independent samples then K-S two sample test can be used to test the agreement between two cumulative distributions. The null hypothesis states that there is no difference between the two distributions. The D-statistic is calculated in the same manner as the K-S One Sample Test.

${D = Maximum |{F_n}_1(X)-{F_n}_2(X)|}$

${n_1}$ = Observations from first sample.

${n_2}$ = Observations from second sample.

It has been seen that when the cumulative distributions show large maximum deviation ${|D|}$ it is indicating towards a difference between the two sample distributions.

The critical value of D for samples where ${n_1 = n_2}$ and is ≤ 40, the K-S table for two sample case is used. When ${n_1}$ and/or ${n_2}$ > 40 then the K-S table for large samples of two sample test should be used. The null hypothesis is accepted if the calculated value is less than the table value and vice-versa.

Thus use of any of these nonparametric tests helps a researcher to test the significance of his results when the characteristics of the target population are unknown or no assumptions had been made about them.

To Continue Learning Please Login

The Kolmogorov-Smirnov Test ¶

A visit to a data and statistical technique useful to software engineers. We learn about some Rust too along the way.

The code and examples here are available on Github . The Rust library is on crates.io .

Kolmogorov-Smirnov Hypothesis Testing ¶

The Kolmogorov-Smirnov test is a hypothesis test procedure for determining if two samples of data are from the same distribution. The test is non-parametric and entirely agnostic to what this distribution actually is. The fact that we never have to know the distribution the samples come from is incredibly useful, especially in software and operations where the distributions are hard to express and difficult to calculate with.

It is really surprising that such a useful test exists. This is an unkind Universe, we should be completely on our own.

The test description may look a bit hard in the outline below but skip ahead to the implementation because the Kolmogorov-Smirnov test is incredibly easy in practice.

The Kolmogorov-Smirnov test is covered in Numerical Recipes . There is a pdf available from the third edition of Numerical Recipes in C.

The Wikipedia article is a useful overview but light about proof details. If you are interested in why the test statistic has a distribution that is independent and useful for constructing the test then these MIT lecture notes give a sketch overview.

See this introductory talk by Toufic Boubez at Monitorama for an application of the Kolmogorov-Smirnov test to metrics and monitoring in software operations. The slides are available on slideshare .

The Test Statistic ¶

To do this we devise a single number calculated from the samples, i.e. a statistic. The trick is to find a statistic which has a range of values that do not depend on things we do not know. Like the actual underlying distributions in this case.

The test statistic in the Kolmogorov-Smirnov test is very easy, it is just the maximum vertical distance between the empirical cumulative distribution functions of the two samples. The empirical cumulative distribution of a sample is the proportion of the sample values that are less than or equal to a given value.

As an aside, these examples demonstrate an important note about the application of the Kolmogorov-Smirnov test. It is much better at detecting distributional differences when the sample medians are far apart than it is at detecting when the tails are different but the main mass of the distributions is around the same values.

The empirical cumulative distribution function is an unbiased estimator for the underlying cumulative distribution function, incidentally.

Two Sample Test ¶

Tables of critical values are available, for instance the SOEST tables describe a test implementation for samples of more than twelve where we reject the null hypothesis, i.e. decide that the samples are from different distributions, if:

Alternatively, Numerical Recipes describes a direct calculation that works well for:

Numerical Recipes continues by claiming the probability that the test statistic is greater than the value observed is approximately:

This can be computed by summing terms until a convergence criterion is achieved. The implementation in Numerical Recipes gives this a hundred terms to converge before failing.

The difference between the two approximations is marginal. The Numerical Recipes approach produces slightly smaller critical values for rejecting the null hypothesis as can be seen in the following plot of critical values for the 95% confidence level where one of the samples has size 256. The x axis varies over the other sample size, the y axis being the critical value.

The SOEST tables are an excellent simplifying approximation.

Discussion ¶

A straightforward implementation of this test can be found in the Github repository . Calculating the test statistic using the empirical cumulative distribution functions is probably as complicated as it gets for this. There are two versions of the test statistic calculation in the code, the simpler version being used to probabilistically verify the more efficient implementation.

Non-parametricity and generality are the great advantages of the Kolmogorov-Smirnov test but these are balanced by drawbacks in ability to establish sufficient evidence to reject the null hypothesis.

The Chi-squared test is also used for testing whether samples are from the same distribution but this is done with a binning discretization of the data. The Kolmogorov-Smirnov test does not require this.

A Field Manual for Rust ¶

Rust is a Mozilla sponsored project to create a safe, fast systems language. There is an entire free O’Reilly book on why create this new language but the reasons include:

• Robust memory management. It is impossible to deference null or dangling pointers in Rust.
• Improved security, reducing the incidence of flaws like buffer overflow exploits.
• A light runtime with no garbage collection and overhead means Rust is ideal to embed in other languages and platforms like Ruby, Python, and Node.
• Rust has many modern language features unavailable in other systems languages.

Rust is a serious language, capable of very serious projects. The current flagship Rust project, for instance, is Servo , a browser engine under open source development with contributions from Mozilla and Samsung.

The best introduction to Rust is the Rust Book . Newcomers should also read Steve Klabnik’s alternative introduction to Rust for the upfront no-nonsense dive into memory ownership, the crux concept for Rust beginners.

Those in a hurry can quickstart with these slide decks by:

• Dimiter Petrov and Romain Ruetschi
• Danilo Bargen

Two must-read learning resources are 24 Days of Rust , a charming tour around the libraries and world of Rust, and ArcadeRS , a tutorial in Rust about writing video games.

And finally, if Servo has you interested in writing a browser engine in Rust, then Let’s build a browser engine! is the series for you. It walks through creating a simple HTML rendering engine in Rust.

Moral Support for Learning the Memory Rules ¶

The Road to Rust is not royal, there is no pretending otherwise. The Rust memory rules about lifetime, ownership, and borrowing are especially hard to learn.

It probably doesn’t much feel like it but Rust is really trying to help us with these rules. And to be fair to Rust, it hasn’t segfaulted me so far.

But that is no comfort when the compiler won’t build your code and you can’t figure out why. The best advice is probably to read as much about the Rust memory rules as you can and to keep reading about them over and over until they start to make some sense. Don’t worry, everybody finds it difficult at first.

Although adherence to the rules provides the compiler with invariant guarantees that can be used to construct proofs of memory safety, the rationale for these rules is largely unimportant. What is necessary is to find a way to work with them so your programs compile.

Remember too that learning to manage memory safely in C/C++ is much harder than learning Rust and there is no compiler checking up on you in C/C++ to make sure your memory management is correct.

Keep at it. It takes a long time but it does become clearer!

Niche Observations ¶

This section is a scattering of Rust arcana that caught my attention. Nothing here that doesn’t interest you is worth troubling too much with and you should skip on past.

Travis CI has excellent support for building Rust projects, including with the beta and nightly versions. It is simple to set up by configuring a travis.yml according to the Travis Rust documentation . See the Travis CI build for this project for an example.

Rust has a formatter in rustfmt and a lint in rust-clippy . The formatter is a simple install using cargo install and provides a binary command. The lint requires more integration into your project, and currently also needs the nightly version of Rust for plugin support. Both projects are great for helping Rust newcomers.

Foreign Function Interface is an area where Rust excels. The absence of a large runtime means Rust is great for embedding in other languages and it has a wide range as a C replacement in writing modules for Python, Ruby, Node, etc. The Rust Book introduction demonstrates how easy it is call Rust from other languages. Day 23 of Rust and the Rust FFI Omnibus are additional resources for Rust FFI.

Rust is being used experimentally for embedded development. Zinc is work on building a realtime ARM operating system using Rust primarily, and the following are posts about building software for embedded devices directly using Rust.

• Rust bare metal on ARM microcontroller .
• Embedded Rust Right Now!

Relatedly, Rust on Raspberry Pi is a guide to cross-compiling Rust code for the Raspberry Pi.

Rust treats the code snippets in your project documentation as tests and makes a point of compiling them. This helps keep documentation in sync with code but it is a shock the first time you get a compiler error for a documentation code snippet and it takes you ages to realise what is happening.

Kolmogorov-Smirnov Library ¶

The Kolmogorov-Smirnov test implementation is available as a Cargo crate , so it is simple to incorporate into your programs. Add the dependency to your Cargo.toml file.

Then to use the test, call the kolmogorov_smirnov::test function with the two samples to compare and the desired confidence level.

The Kolmogorov-Smirnov test as implemented works for any data with a Clone and an Ord trait implementation in Rust. So it is possible, but pretty useless, to test samples of characters, strings and lists. In truth, the Kolmogorov-Smirnov test requires the samples to be taken from a continuous distribution, so discrete data like characters and strings are cute to consider but invalid test data.

Still being strict, this test condition also does not hold for integer data unless some hands are waved about the integer data being embedded into real numbers and a distribution cooked up from the probability weights. We make some compromises and allowances.

If you have floating point or integer data to test, you can use the included test runner binaries, ks_f64 and ks_i32 . These operate on single-column headerless data files and test two commandline argument filenames against each other at 95% confidence.

Testing floating point numbers is a headache because Rust floating point types (correctly) do not implement the Ord trait, only the PartialOrd trait. This is because things like NaN are not comparable and the order cannot be total over all values in the datatype.

The test runner for floating point types is implemented using a wrapper type that implements a total order, crashing on unorderable elements. This suffices in practice since the unorderable elements will break the test anyway.

The implementation uses the Numerical Recipes approximation for rejection probabilities rather than the almost as accurate SOEST table approximation for critical values. This allows the additional reporting of the reject probability which isn’t available using the SOEST approach.

Statistical tests are more fun if you have datasets to run them over.

Because it is traditional and because it is easy and flexible, start with some normally distributed data.

Rust can generate normal data using the rand::distributions module. If mean and variance are f64 values representing the mean and variance of the desired normal deviate, then the following code generates the deviate. Note that the Normal::new call requires the mean and standard deviation as parameters, so it is necessary to take the square root of the variance to provide the standard deviation value.

The kolmogorov_smirnov library includes a binary for generating sequences of independently distributed Normal deviates. It has the following usage.

The -q option is useful too for suppressing cargo build messages in the output.

The following is a plot of all three datasets to illustrate the relative widths, heights and supports.

Save yourself the trouble in reproduction by running this instead:

This failure is a demonstration of how the Kolmogorov-Smirnov test is sensitive to location because here the mean of the dat/normal_0_2.1.tsv is shifted quite far from the origin.

This is the density.

And superimposed with the density from dat/normal_0_2.tsv .

The data for dat/normal_0_2.1.tsv is the taller density in this graph. Notice, in particular, that the mean is shifted left a lot in comparison with dat/normal_0_2.tsv . See also the chunks of non-overlapping weight on the left and right hand slopes.

Looking at the empirical cumulative density functions of the false negative comparison, we see a significant gap between the curves starting near 0.

One false negative in thirty unique test pairs at 95% confidence is on the successful side of expectations.

Turning instead to tests that should be expected to fail, the following block runs comparisons between datasets from different distributions.

dat/normal_0_1.2.tsv is reported incorrectly as being from the same distribution as the following datasets.

Similarly, dat/normal_0_1.3.tsv is a false positive against:

And dat/normal_0_1.4.tsv is a false positive against:

Note that many of these false positives have rejection probabilities that are high but fall short of the 95% confidence level required. The null hypothesis is that the distributions are the same and it is this that must be challenged at the 95% level.

Let’s examine the test where the rejection probability is lowest, that between dat/normal_0_1.2.tsv and dat/normal_0_2.2.tsv .

The overlaid density and empirical cumulative density functions show strong difference.

There is insufficient evidence to reject the null hypothesis.

Let’s also examine the false positive test where the rejection probability is tied highest, between dat/normal_0_1.4.tsv and dat/normal_0_2.1.tsv .

This is just incredibly borderline. There is a very strong difference on the left side but it falls fractionally short of the required confidence level. Note how this also illustrates the bias in favour of the null hypothesis that the two samples are from the same distribution.

Notice that of the false positives, only the one between dat/normal_0_1.2.tsv and dat/normal_0_2.tsv happens with a dataset containing more than 256 samples. In this test with 8192 samples against 256, the critical value is 0.0855 and the test statistic scrapes by underneath at 0.08288.

In the case for two samples of size 8192, the critical value is a very discriminating 0.02118.

In total there are ten false positives in 75 tests, a poor showing.

The lesson is that false positives are more common and especially with small datasets. When using the Kolmogorov-Smirnov test in production systems, tend to use higher confidence levels when larger datasets cannot be available.

http://twitter.com Response Times ¶

Less artificially, and more representative of metrics in software operations and monitoring, are datasets of HTTP server response times. Metrics which behave like response time are very typical and not easy to analyse with usual statistical technology.

Apache Bench is a commandline URL loadtesting tool that can be used to collect sample datasets of HTTP request times. A dataset of service times for http://twitter.com was collected using:

The test actually ships 3.36MB of redirect headers since http://twitter.com is a 301 Moved Permanently redirect to https://twitter.com but the dataset is still useful as it exhibits the behaviour of HTTP endpoint responses anyway.

The options in the call specify:

• -c 1 : Use test concurrency of one outstanding request to throttle the testing.
• -v 3 : Log at high verbosity level to show individual request data.
• -g http.tsv : Output a TSV summary to http.tsv . The -g stands for Gnuplot which the output file is organised to support particularly.

A timeout or significant failure can trash the test completely, so it is more robust to collect data in blocks of 256 requests and combine the results. This was done in collect some supplementary data for comparison purposes and is available as dat/http.1.tsv through dat/http.4.tsv in the Github repository . The primary dataset is dat/http.tsv .

Aside: The trailing / in the target URL is required in the ab command or it fails with an invalid URL error.

The result data file from Apache Bench has the following schema :

• starttime : A human friendly time representation of the request start.
• seconds : The Unix epoch seconds timestamp of starttime . This is the number of regular, but not leap, seconds since 1 January 1970. Trivia Fact: this is why Unix timestamps line up, against sane expectations, on minute boundaries when divided by 60.
• ctime : Connection time to the server in milliseconds.
• dtime : Processing time on the server in milliseconds. The d may stand for “duration” or it may not.
• ttime : Total time in milliseconds, ctime + dtime .
• wait : Waiting time in milliseconds. This is not included in ttime , it appears from the data.

If you want to use the generated data file as it was intended for processing with Gnuplot, then see this article .

The output data is sorted by Apache Bench according to ttime , meaning shorter requests come first in the output. The purposes here better appreciate data sorted by the seconds timestamp, particularly to plot the timeseries data in the order the requests were issued.

And because nobody is much interested in when exactly this dataset was made, the starttime and seconds fields are dropped from the final data. The following crafty piece of Awk does the header-retaining sort and column projection.

All the response time datasets in the Github repository have been processed like this.

To transform the headered multi-column data files into a format suitable for input to ks_i64 use the following example as a guide:

Then to run the test:

The timeseries plot shows a common Internet story of outliers, failure cases and disgrace.

The density is highly peaked but includes fast failure weight and a long light tail. This is not straightforward to parametrise with the common statistical distributions that are fruitful to work with and demonstrates the significant utility of the Kolmogorov-Smirnov test.

Note there is a much larger horizontal axis range in this graph. This has the effect of compressing the visual area under the graph relative to the earlier dataset density plots.

Don’t let this trick you. The y axis values are smaller than in the other graphs but there is far more horizontal axis support to compensate. The definition of a probability density means the area under the graph in all the density plots must sum to the same.

Restricting attention to just the total time value, there are ten test dataset combinations all of which are false negatives save for the comparison between dat/http_ttime.1.tsv dat/http_ttime.4.tsv

The only accepted test returned the following test information:

Here is the timeseries and density plot for ttime in the dat/http_ttime.1.tsv dataset for comparison to the dat/http_ttime.tsv plots above.

There is some similarity to the observations in dat/http_ttime.tsv but there is a far shorter tail here.

In fact, the datasets are all very different from each other. Here are the other density plots.

dat/http_ttime.2.tsv exhibits a spike of failures which are of short duration and contribute large weight on the left of the graph.

By contrast dat/http_ttime.3.tsv has no fast failures or slow outliners and the weight is packed around .9s to 1s.

dat/http_ttime.4.tsv has a long tail for an outlier, likely to be request timeouts.

By inspection of the empirical cumulative density functions, the only test with a possible chance of accepting the null hypothesis was that between dat/http_ttime.tsv and dat/http_ttime.4.tsv . This is the comparison with the smallest test statistic from the rejected cases.

Even still, this is not a close match. The empirical cumulative density function plots show very different profiles on the error request times to the left of the diagram.

As for the passing match, it turns out that dat/http_ttime.1.tsv and dat/http_ttime.4.tsv are indeed quite similar. This would be more apparent but for the outlier in dat/http_ttime.4.tsv . Given that the Kolmogorov-Smirnov test is not sensitive at the tails, this does not contribute evidence to reject the null hypothesis.

In conclusion, the captured HTTP response time datasets exhibit features which make them likely to actually be from different distributions, some with and without long outliers, fast errors.

Twitter, Inc. Stock Price ¶

The final dataset is a historical stock market sample. Collect a fortnight of minute granularity stock price data from Google Finance using:

The HTTP parameters in the call specify:

• i=60 : This is the sample interval in seconds, i.e. get per-minute data. The minimum sample interval available is sixty seconds.
• p=14d : Return data for the previous fourteen days.
• f=d,c,h,l,o,v : Include columns in the result for sample interval start date, closing price, high price value, low price value, opening price, and trade count, i.e. volume.
• q=TWTR : Query data for the TWTR stock symbol.

The response includes a header block before listing the sample data which looks like the following:

Lines starting with an a character include an absolute timestamp value. Otherwise, the timestamp field value is an offset and has to be added to the timestamp value in the last previous absolute timestamp line to get the absolute timestamp for the given line.

This Awk script truncates the header block and folds the timestamp offsets into absolute timestamp values.

The output TSV file is provided as dat/twtr.tsv in the Github repository .

A supplementary dataset consisting of a single day was collected for comparison purposes and is available as dat/twtr.1.tsv . It was processed in the same manner as dat/twtr.tsv . The collection command was:

Trading hours on the New York Stock Exchange are weekdays 9.30am to 4pm. This results in long horizontal line segments for missing values in the timeseries plot for interval opening prices, corresponding to the overnight and weekend market close periods.

The following is the minutely opening price density plot.

The missing value graph artifact is more pronounced in the minutely trading volume timeseries. The lines joining the trading day regions should be disregarded.

Finally, the trading volume density plot is very structured, congregating near the 17,000 trades/minute rate.

The reader is invited to analyse the share price as an exercise. Let me know from your expensive yacht if you figure it out and make a fortune.

A Diversion In QuickCheck ¶

QuickCheck is crazy amounts of fun writing tests and a great way to become comfortable in a new language.

The idea in QuickCheck is to write tests as properties of inputs rather than specific test cases. So, for instance, rather than checking whether a given pair of samples have a determined maximum empirical cumulative distribution function distance, instead a generic property is verified. This property can be as simple as the distance is between zero and one for any pair of input samples or as constrictive as the programmer is able to create.

This form of test construction means QuickCheck can probabilistically check the property over a huge number of test case instances and establish a much greater confidence of correctness than a single individual test instance could.

It can be harder too, yes. Writing properties that tightly specify the desired behaviour is difficult but starting with properties that very loosely constrain the software behaviour is often helpful, facilitating an evolution into more sharply binding criteria.

For a tutorial introduction to QuickCheck, John Hughes has a great introduction talk .

There is an implementation of QuickCheck for Rust and the tests for the Kolmogorov-Smirnov Rust library have been implemented using it. See the Github repository for examples of how to QuickCheck in Rust.

Here is a toy example of a QuickCheck property to test an integer doubling function.

This test is broken and QuickCheck makes short(I almost wrote ‘quick’!) work of letting us know that we have been silly.

The last log line includes the u32 value that failed the test, i.e. zero. Correct practice is to now create a non-probabilistic test case that tests this specific value. This protects the codebase from regressions in the future.

The problem in the example is that the property is not actually valid for the double function because double zero is not actually greater than zero. So let’s fix the test.

Note also how QuickCheck produced a minimal test violation, there are no smaller values of u32 that violated the test. This is not an accident, QuickCheck libraries often include features for shrinking test failures to minimal examples. When a test fails, QuickCheck will often rerun it searching successively on smaller instances of the test arguments to determine the smallest violating test case.

The function is still broken, by the way, because it overflows for large input values. The Rust QuickCheck doesn’t catch this problem because the QuickCheck::quickcheck convenience runner configures the tester to produce random data between zero and one hundred, not in the range where the overflow will be evident. For this reason, you should not use the convenience runner in testing. Instead, configure the QuickCheck manually with as large a random range as you can.

This will break the test with an overflow panic. This is correct and the double function should be reimplemented to do something about handling overflow properly.

A warning, though, if you are testing vec or string types. The number of elements in the randomly generated vec or equivalently, the length of the generated string will be between zero and the size in the StdGen configured. There is the potential in this to create unnecessarily huge vec and string values. See the example of NonEmptyVec below for a technique to limit the size of a randomly generated vec or string while still using StdGen with a large range.

Unfortunately, you are out of luck on a 32-bit machine where the usize::MAX will only get you to sampling correctly in u32 . You will need to upgrade to a new machine before you can test u64 , sorry.

By way of example, it is actually more convenient to include known failure cases like u32::max_value() in the QuickCheck test function rather than in a separate traditional test case function. So, when the QuickCheck fails for the overflow bug, add the test case like follows instead of as a new function:

Sometimes the property to test is not valid on some test arguments, i.e. the property is useful to verify but there are certain combinations of probabilistically generated inputs that should be excluded.

The Rust QuickCheck library supports this with TestResult . Suppose that instead of writing the double test property correctly, we wanted to just exclude the failing cases instead. This might be a practical thing to do in a real scenario and we can rewrite the test as follows:

Here, the cases where the property legitimately doesn’t hold are excluded by returning``TestResult::discard()``. This causes QuickCheck to retry the test with the next randomly generated value instead.

Note also that the function return type is now TestResult and that TestResult::from_bool is needed for the test condition.

An alternative approach is to create a wrapper type in the test code which only permits valid input and to rewrite the tests to take this type as the probabilistically generated input instead.

For example, suppose you want to ensure that QuickCheck only generates positive integers for use in your property verification. You add a wrapper type PositiveInteger and now in order for QuickCheck to work, you have to implement the Arbitrary trait for this new type.

The minimum requirement for an Arbitrary implementation is a function called arbitrary taking a Gen random generator and producing a random PositiveInteger . New implementations should always leverage existing Arbitrary implementations, and so PositiveInteger generates a random u64 using u64::arbitrary() and constrains it to be greater than zero.

Note also the implementation of shrink() here, again in terms of an existing u64::shrink() . This method is optional and unless implemented QuickCheck will not minimise property violations for the new wrapper type.

Use PositiveInteger like follows:

There is no need now for TestResult::discard() to ignore the failure case for zero.

Finally, wrappers can be added for more complicated types too. A commonly useful container type generator is NonEmptyVec which produces a random vec of the parameterised type but excludes the empty vec case. The generic type must itself implement Arbitrary for this to work.

Thank you to Timur Abishev, James Harlow, and Pascal Hartig for kind suggestions and errata.

Table Of Contents

• The Test Statistic
• Two Sample Test
• Moral Support for Learning the Memory Rules
• Niche Observations
• Kolmogorov-Smirnov Library
• A Diversion In QuickCheck

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

7.5 - tests for error normality.

To complement the graphical methods just considered for assessing residual normality, we can perform a hypothesis test in which the null hypothesis is that the errors have a normal distribution. A large p -value and hence failure to reject this null hypothesis is a good result. It means that it is reasonable to assume that the errors have a normal distribution. Typically, assessment of the appropriate residual plots is sufficient to diagnose deviations from normality. However, a more rigorous and formal quantification of normality may be requested. So this section provides a discussion of some common testing procedures (of which there are many) for normality. For each test discussed below, the formal hypothesis test is written as:

\(\begin{align*} \nonumber H_{0}&\colon \textrm{the errors follow a normal distribution} \\ \nonumber H_{A}&\colon \textrm{the errors do not follow a normal distribution}. \end{align*}\)

While hypothesis tests are usually constructed to reject the null hypothesis, this is a case where we actually hope we fail to reject the null hypothesis as this would mean that the errors follow a normal distribution.

Anderson-Darling Test Section  

The Anderson-Darling Test measures the area between a fitted line (based on the chosen distribution) and a nonparametric step function (based on the plot points). The statistic is a squared distance that is weighted more heavily in the tails of the distribution. Smaller Anderson-Darling values indicate that the distribution fits the data better. The test statistic is given by:

\(\begin{equation*} A^{2}=-n-\sum_{i=1}^{n}\frac{2i-1}{n}(\log \textrm{F}(e_{i})+\log (1-\textrm{F}(e_{n+1-i}))), \end{equation*}\)

where \(\textrm{F}(\cdot)\) is the cumulative distribution of the normal distribution. The test statistic is compared against the critical values from a normal distribution in order to determine the p -value.

The Anderson-Darling test is available in some statistical software. To illustrate here's statistical software output for the example on IQ and physical characteristics from Lesson 5 ( IQ Size data ), where we've fit a model with PIQ as the response and Brain and Height as the predictors:

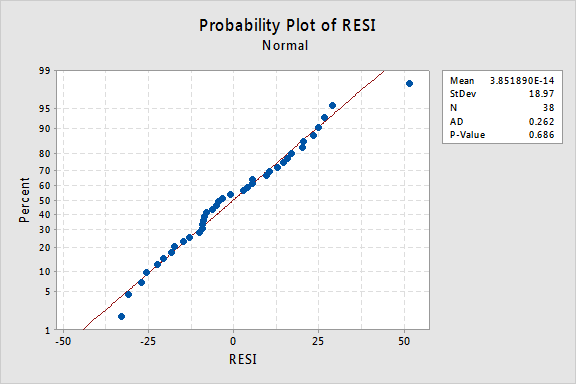
Since the Anderson-Darling test statistic is 0.262 with an associated p -value of 0.686, we fail to reject the null hypothesis and conclude that it is reasonable to assume that the errors have a normal distribution

Shapiro-Wilk Test Section  

The Shapiro-Wilk Test uses the test statistic

\(\begin{equation*} W=\dfrac{\biggl(\sum_{i=1}^{n}a_{i}e_{(i)}\biggr)^{2}}{\sum_{i=1}^{n}(e_{i}-\bar{e})^{2}}, \end{equation*} \)

where \(e_{i}\) pertains to the \(i^{th}\) largest value of the error terms and the \(a_i\) values are calculated using the means, variances, and covariances of the \(e_{i}\). W is compared against tabulated values of this statistic's distribution. Small values of W will lead to the rejection of the null hypothesis.

The Shapiro-Wilk test is available in some statistical software. For the IQ and physical characteristics model with PIQ as the response and Brain and Height as the predictors, the value of the test statistic is 0.976 with an associated p-value of 0.576, which leads to the same conclusion as for the Anderson-Darling test.

Ryan-Joiner Test Section  

The Ryan-Joiner Test is a simpler alternative to the Shapiro-Wilk test. The test statistic is actually a correlation coefficient calculated by

\(\begin{equation*} R_{p}=\dfrac{\sum_{i=1}^{n}e_{(i)}z_{(i)}}{\sqrt{s^{2}(n-1)\sum_{i=1}^{n}z_{(i)}^2}}, \end{equation*}\)

where the \(z_{(i)}\) values are the z -score values (i.e., normal values) of the corresponding \(e_{(i)}\) value and \(s^{2}\) is the sample variance. Values of \(R_{p}\) closer to 1 indicate that the errors are normally distributed.

The Ryan-Joiner test is available in some statistical software. For the IQ and physical characteristics model with PIQ as the response and Brain and Height as the predictors, the value of the test statistic is 0.988 with an associated p-value > 0.1, which leads to the same conclusion as for the Anderson-Darling test.

Kolmogorov-Smirnov Test Section  

The Kolmogorov-Smirnov Test (also known as the Lilliefors Test ) compares the empirical cumulative distribution function of sample data with the distribution expected if the data were normal. If this observed difference is sufficiently large, the test will reject the null hypothesis of population normality. The test statistic is given by:

\(\begin{equation*} D=\max(D^{+},D^{-}), \end{equation*}\)

\(\begin{align*} D^{+}&=\max_{i}(i/n-\textrm{F}(e_{(i)}))\\ D^{-}&=\max_{i}(\textrm{F}(e_{(i)})-(i-1)/n), \end{align*}\)

The test statistic is compared against the critical values from a normal distribution in order to determine the p -value.

The Kolmogorov-Smirnov test is available in some statistical software. For the IQ and physical characteristics model with PIQ as the response and Brain and Height as the predictors, the value of the test statistic is 0.097 with an associated p -value of 0.490, which leads to the same conclusion as for the Anderson-Darling test.

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes

Kolmogorov-Smirnov Test (KS Test)

• ML | Kolmogorov-Smirnov Test
• Kolmogorov-Smirnov Test in R Programming
• Shapiro–Wilk Test in R Programming
• Python - Test if common values are greater than K
• How to Perform a Shapiro-Wilk Test in Python
• Python - Kolmogorov-Smirnov Distribution in Statistics
• Tukey-Kramer Test for Post Hoc Analysis
• How to Perform Runs Test in R
• Primality Test | Set 3 (Miller–Rabin)
• Code Coverage Testing in Software Testing
• Random Testing in Software Testing
• Kruskal-Wallis test in R Programming
• AKS Primality Test
• KPMG Recruitment Process
• Fligner-Killeen Test in R Programming
• Sign Test in R
• Bartlett’s Test in R Programming
• Principles of software testing - Software Testing
• JavaScript Program for Kruskal-Wallis Test Calculator

The Kolmogorov-Smirnov (KS) test is a non-parametric method for comparing distributions, essential for various applications in diverse fields.

In this article, we will look at the non-parametric test which can be used to determine whether the shape of the two distributions is the same or not.

What is Kolmogorov-Smirnov Test?

Kolmogorov–Smirnov Test is a completely efficient manner to determine if two samples are significantly one of a kind from each other. It is normally used to check the uniformity of random numbers. Uniformity is one of the maximum important properties of any random number generator and the Kolmogorov–Smirnov check can be used to check it.

The Kolmogorov–Smirnov test is versatile and can be employed to evaluate whether two underlying one-dimensional probability distributions vary. It serves as an effective tool to determine the statistical significance of differences between two sets of data. This test is particularly valuable in various fields, including statistics, data analysis, and quality control, where the uniformity of random numbers or the distributional differences between datasets need to be rigorously examined.

Kolmogorov Distribution

The Kolmogorov distribution, often denoted as D, represents the cumulative distribution function (CDF) of the maximum difference between the empirical distribution function of the sample and the cumulative distribution function of the reference distribution.

The probability distribution function (PDF) of the Kolmogorov distribution itself is not expressed in a simple analytical form. Instead, tables or statistical software are commonly used to obtain critical values for the test. The distribution is influenced by sample size, and the critical values depend on the significance level chosen for the test.

• n is the sample size.
• x is the normalized Kolmogorov-Smirnov statistic.
• k is the index of summation in the series

How does Kolmogorov-Smirnov Test work?

Below are the steps for how the Kolmogorov-Smirnov test works:

• Null Hypothesis : The sample follows a specified distribution.
• Alternative Hypothesis: The sample does not follow the specified distribution.
• A theoretical distribution (e.g., normal, exponential) is decided against which you want to test the sample distribution. This distribution is usually based on theoretical expectations or prior knowledge.
• For a one-sample Kolmogorov-Smirnov test, the test statistic (D) represents the maximum vertical deviation between the empirical distribution function (EDF) of the sample and the cumulative distribution function (CDF) of the reference distribution.
• For a two-sample Kolmogorov-Smirnov test, the test statistic compares the EDFs of two independent samples.
• The test statistic (D) is compared to a critical value from the Kolmogorov-Smirnov distribution table or, more commonly, a p-value is calculated.
• If the p-value is less than the significance level (commonly 0.05), the null hypothesis is rejected, suggesting that the sample distribution does not match the specified distribution.
• If the null hypothesis is rejected, it indicates that there is evidence to suggest that the sample does not follow the specified distribution. The alternative hypothesis, suggesting a difference, is accepted.

When use Kolmogorov-Smirnov Test?

The main idea behind using this Kolmogorov-Smirnov Test is to check whether the two samples that we are dealing with follow the same type of distribution or if the shape of the distribution is the same or not.

Let’s a breakdown the scenarios where this test can be applicable:

• Comparison of Probability Distributions : The test is used to evaluate whether two samples exhibit the same probability distribution.
• Compare the shape of the distributions : If we assume that the shapes or probability distributions of the two samples are similar, the test assesses the maximum absolute difference between the cumulative probability distributions of the two functions.
• Check Distributional Differences: The test quantifies the maximum difference between the cumulative probability distributions, and a higher value indicates greater dissimilarity in the shape of the distributions.
• Parametric Test
• Non-Parametric Test

One Sample Kolmogorov-Smirnov Test

The one-sample Kolmogorov-Smirnov (KS) test is used to determine whether a sample comes from a specific distribution. It is particularly useful when the assumption of normality is in question or when dealing with small sample sizes .

Empirical Distribution Function

The empirical distribution function at the value x represents the proportion of data points that are less than or equal to x in the sample. The function can be defined as:

• n is the number of observations in the sample

Kolmogorov–Smirnov Statistic

• sup stands for supremum, which means the largest value over all possible values of x.

• Compute the Empirical Distribution Function

• Calculate the Kolmogorov–Smirnov Statistic
• Compare KS static with Critical Value or P-value

Kolmogorov-Smirnov Test Python One-Sample

• The statistic is relatively small (0.103), suggesting that the EDF and CDF are close.
• Since the p-value (0.218) is greater than the chosen significance level (commonly 0.05), we fail to reject the null hypothesis.

Therefore, we cannot conclude that the sample does not come from the specified distribution (normal distribution with mean and standard deviation).

Two-Sample Kolmogorov–Smirnov Test

The two-sample Kolmogorov-Smirnov (KS) test is used to compare two independent samples to assess whether they come from the same distribution. It’s a distribution-free test that evaluates the maximum vertical difference between the empirical distribution functions (EDFs) of the two samples.

Empirical Distribution Function (EDF):

The empirical distribution function at the value ( x ) in each sample represents the proportion of observations less than or equal to ( x ). Mathematically, the EDFs for the two samples are given by:

For Group 1:

For Group 2:

• sup denotes supremum, representing the largest value over all possible xx values,

• Each ECDF represents the proportion of observations in the corresponding sample that are less than or equal to a particular value of  x .

Let’s perform the Two-Sample Kolmogorov–Smirnov Test using the scipy.stats.ks_2samp function. The function calculates the Kolmogorov–Smirnov statistic for two samples to find out if two samples come from different distributions or not.

Kolmogorov-Smirnov Test Python Two-Sample

• The null hypothesis assumes that the two samples come from the same distribution.
• The decision is based on comparing the p-value with a chosen significance level (e.g., 0.05). If the p-value is less than the significance level, reject the null hypothesis, indicating that the two samples come from different distributions.
• The statistic is, indicating a relatively large discrepancy between the two sample distributions.
• The small p-value suggests strong evidence against the null hypothesis that the two samples come from the same distribution.

Therefore, two samples come from different distributions.

One-Sample KS Test vs Two-Sample KS Test

Multidimensional kolmogorov-smirnov testing.

The Kolmogorov-Smirnov (KS) test, in its traditional form, is designed for one-dimensional data, where it assesses the similarity between the empirical distribution function (EDF) and a theoretical or another empirical distribution along a single axis. However, when dealing with data in more than one dimension, the extension of the KS test becomes more complex.

In the context of multidimensional data, the concept of the Kolmogorov-Smirnov statistic can be adapted to evaluate differences across multiple dimensions. This adaptation often involves considering the maximum distance or discrepancy in the cumulative distribution functions along each dimension. A generalization of the KS test to higher dimensions is known as the Kolmogorov-Smirnov n-dimensional test.

The Kolmogorov-Smirnov n-dimensional test aims to evaluate whether two samples in multiple dimensions follow the same distribution. The test statistic becomes a function of the maximum differences in cumulative distribution functions along each dimension.

Applications of the Kolmogorov-Smirnov Test

The essential features of the use of the Kolmogorov-Smirnov test are:

Goodness-of-in shape attempting out

The KS check can be used to evaluate how nicely a pattern data set fits a hypothesized distribution. This may be beneficial in determining whether or now not a sample of facts is probable to have been drawn from a particular distribution, together with a ordinary distribution or an exponential distribution. This is frequently used in fields together with finance, engineering, and herbal sciences to verify whether a records set conforms to an predicted distribution, which could have implications for preference-making, version fitting, and prediction.

Two-sample comparison

The KS test is used to evaluate two facts units to decide whether or not they’re drawn from the same                     underlying distribution. This may be beneficial in assessing whether there are statistically giant differences among  statistics units, together  with comparing the overall performance of  tremendous companies in an test or evaluating the distributions of two precise variables.

It is normally utilized in fields together with social sciences, remedy, and agency to evaluate whether or not there are full-size variations among groups or populations.

Hypothesis sorting Out

Check unique hypotheses about the distributional residences of a records set. For instance, it is able to be used to check whether a facts set is normally distributed or whether or not it follows a specific theoretical distribution. This may be beneficial in verifying assumptions made in statistical analyses or validating version assumptions.

Non-parametric alternative

The K-S test is a non-parametric test, because of this it does no longer require assumptions about the form or         parameters of the underlying distributions being in contrast. This makes it a beneficial opportunity to parametric checks, in conjunction with the t-test or ANOVA, at the same time as facts do no longer meet the assumptions of these assessments, along with at the same time as statistics are not generally disbursed, have unknown or unequal variances, or have small pattern sizes.

Limitations of the Kolmogorov-Smirnov Test

• Sensitivity to sample length: K-S check may additionally moreover have confined energy with small sample sizes and may yield statistically sizeable results with large sample sizes even for small versions.
• Assumes independence: K-S test assumes that the records gadgets being compared are unbiased, and might not be appropriate for based facts.
• Limited to non-stop records: K-S take a look at is designed for non-stop statistics and won’t be suitable for discrete or specific information without modifications.
• Lack of sensitivity to precise distributional properties: K-S test assesses fashionable differences among distributions and might not be touchy to variations specially distributional houses.
• Vulnerability to type I error with multiple comparisons: Multiple K-S exams or use of K-S test in a larger hypothesis checking out framework might also boom the threat of type I mistakes.

While versatile, the KS test demands caution in sample size considerations, assumptions, and interpretations to ensure robust and accurate analyses.

Kolmogorov-Smirnov test- FAQs

Q. what is kolmogorov-smirnov test used for.

Used to assess whether a sample follows a specified distribution or to compare two samples’ distributions.

Q. What is the difference between T test and Kolmogorov-Smirnov test?

T-test compares means of two groups; KS test compares entire distributions for similarity or goodness-of-fit.

Q. How do you interpret Kolmogorov-Smirnov test for normality?

If p-value is high (e.g., > 0.05), data may follow normal distribution; low p-value suggests departure.

Q. How do you interpret KS test p value?

If the p-value is below the chosen significance level (commonly 0.05), we would reject the null hypothesis. It indicates significant difference; large p-value (i.e.below the chosen significance level ) suggests no significant difference.

Q. Which normality test is best?

No one-size-fits-all. Anderson-Darling, Shapiro-Wilk, and KS test are commonly used; choice depends on data size and characteristics.

Please Login to comment...

Similar reads.

• Machine Learning
• Python Programs

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

scipy.stats.kstest #

Performs the (one-sample or two-sample) Kolmogorov-Smirnov test for goodness of fit.

The one-sample test compares the underlying distribution F(x) of a sample against a given distribution G(x). The two-sample test compares the underlying distributions of two independent samples. Both tests are valid only for continuous distributions.

If an array, it should be a 1-D array of observations of random variables. If a callable, it should be a function to generate random variables; it is required to have a keyword argument size . If a string, it should be the name of a distribution in scipy.stats , which will be used to generate random variables.

If array_like, it should be a 1-D array of observations of random variables, and the two-sample test is performed (and rvs must be array_like). If a callable, that callable is used to calculate the cdf. If a string, it should be the name of a distribution in scipy.stats , which will be used as the cdf function.

Distribution parameters, used if rvs or cdf are strings or callables.

Sample size if rvs is string or callable. Default is 20.

Defines the null and alternative hypotheses. Default is ‘two-sided’. Please see explanations in the Notes below.

Defines the distribution used for calculating the p-value. The following options are available (default is ‘auto’):

‘auto’ : selects one of the other options. ‘exact’ : uses the exact distribution of test statistic. ‘approx’ : approximates the two-sided probability with twice the one-sided probability ‘asymp’: uses asymptotic distribution of test statistic

If an int, the axis of the input along which to compute the statistic. The statistic of each axis-slice (e.g. row) of the input will appear in a corresponding element of the output. If None , the input will be raveled before computing the statistic.

Defines how to handle input NaNs.

propagate : if a NaN is present in the axis slice (e.g. row) along which the statistic is computed, the corresponding entry of the output will be NaN.

omit : NaNs will be omitted when performing the calculation. If insufficient data remains in the axis slice along which the statistic is computed, the corresponding entry of the output will be NaN.

raise : if a NaN is present, a ValueError will be raised.

If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the input array.

An object containing attributes:

KS test statistic, either D+, D-, or D (the maximum of the two)

One-tailed or two-tailed p-value.

In a one-sample test, this is the value of rvs corresponding with the KS statistic; i.e., the distance between the empirical distribution function and the hypothesized cumulative distribution function is measured at this observation.

In a two-sample test, this is the value from rvs or cdf corresponding with the KS statistic; i.e., the distance between the empirical distribution functions is measured at this observation.

In a one-sample test, this is +1 if the KS statistic is the maximum positive difference between the empirical distribution function and the hypothesized cumulative distribution function (D+); it is -1 if the KS statistic is the maximum negative difference (D-).

In a two-sample test, this is +1 if the empirical distribution function of rvs exceeds the empirical distribution function of cdf at statistic_location , otherwise -1.

There are three options for the null and corresponding alternative hypothesis that can be selected using the alternative parameter.

two-sided : The null hypothesis is that the two distributions are identical, F(x)=G(x) for all x; the alternative is that they are not identical.

less : The null hypothesis is that F(x) >= G(x) for all x; the alternative is that F(x) < G(x) for at least one x.

greater : The null hypothesis is that F(x) <= G(x) for all x; the alternative is that F(x) > G(x) for at least one x.

Note that the alternative hypotheses describe the CDFs of the underlying distributions, not the observed values. For example, suppose x1 ~ F and x2 ~ G. If F(x) > G(x) for all x, the values in x1 tend to be less than those in x2.

Beginning in SciPy 1.9, np.matrix inputs (not recommended for new code) are converted to np.ndarray before the calculation is performed. In this case, the output will be a scalar or np.ndarray of appropriate shape rather than a 2D np.matrix . Similarly, while masked elements of masked arrays are ignored, the output will be a scalar or np.ndarray rather than a masked array with mask=False .

Suppose we wish to test the null hypothesis that a sample is distributed according to the standard normal. We choose a confidence level of 95%; that is, we will reject the null hypothesis in favor of the alternative if the p-value is less than 0.05.

When testing uniformly distributed data, we would expect the null hypothesis to be rejected.

Indeed, the p-value is lower than our threshold of 0.05, so we reject the null hypothesis in favor of the default “two-sided” alternative: the data are not distributed according to the standard normal.

When testing random variates from the standard normal distribution, we expect the data to be consistent with the null hypothesis most of the time.

As expected, the p-value of 0.92 is not below our threshold of 0.05, so we cannot reject the null hypothesis.

Suppose, however, that the random variates are distributed according to a normal distribution that is shifted toward greater values. In this case, the cumulative density function (CDF) of the underlying distribution tends to be less than the CDF of the standard normal. Therefore, we would expect the null hypothesis to be rejected with alternative='less' :

and indeed, with p-value smaller than our threshold, we reject the null hypothesis in favor of the alternative.

For convenience, the previous test can be performed using the name of the distribution as the second argument.

The examples above have all been one-sample tests identical to those performed by ks_1samp . Note that kstest can also perform two-sample tests identical to those performed by ks_2samp . For example, when two samples are drawn from the same distribution, we expect the data to be consistent with the null hypothesis most of the time.

As expected, the p-value of 0.45 is not below our threshold of 0.05, so we cannot reject the null hypothesis.

Help Center Help Center

• Help Center
• Trial Software
• Product Updates
• Documentation

Two-sample Kolmogorov-Smirnov test

Description

h = kstest2( x1 , x2 ) returns a test decision for the null hypothesis that the data in vectors x1 and x2 are from the same continuous distribution, using the two-sample Kolmogorov-Smirnov test . The alternative hypothesis is that x1 and x2 are from different continuous distributions. The result h is 1 if the test rejects the null hypothesis at the 5% significance level, and 0 otherwise.

h = kstest2( x1 , x2 , Name,Value ) returns a test decision for a two-sample Kolmogorov-Smirnov test with additional options specified by one or more name-value pair arguments. For example, you can change the significance level or conduct a one-sided test.

[ h , p ] = kstest2( ___ ) also returns the asymptotic p -value p , using any of the input arguments from the previous syntaxes.

[ h , p , ks2stat ] = kstest2( ___ ) also returns the test statistic ks2stat .

collapse all

Test Two Samples for the Same Distribution

Generate sample data from two different Weibull distributions.

Test the null hypothesis that data in vectors x1 and x2 comes from populations with the same distribution.

The returned value of h = 1 indicates that kstest rejects the null hypothesis at the default 5% significance level.

Test the Hypothesis at Different Significance Levels

Test the null hypothesis that data vectors x1 and x2 are from populations with the same distribution at the 1% significance level.

The returned value of h = 0 indicates that kstest does not reject the null hypothesis at the 1% significance level.

One-Sided Hypothesis Test

Test the null hypothesis that data in vectors x1 and x2 comes from populations with the same distribution, against the alternative hypothesis that the cdf of the distribution of x1 is larger than the cdf of the distribution of x2 .

The returned value of h = 1 indicates that kstest rejects the null hypothesis, in favor of the alternative hypothesis that the cdf of the distribution of x1 is larger than the cdf of the distribution of x2 , at the default 5% significance level. The returned value of k is the test statistic for the two-sample Kolmogorov-Smirnov test.

Input Arguments

X1 — sample data vector.

Sample data from the first sample, specified as a vector. Data vectors x1 and x2 do not need to be the same size.

Data Types: single | double

x2 — Sample data vector

Sample data from the second sample, specified as a vector. Data vectors x1 and x2 do not need to be the same size.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN , where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Tail','larger','Alpha',0.01 specifies a test using the alternative hypothesis that the empirical cdf of x1 is larger than the empirical cdf of x2 , conducted at the 1% significance level.

Alpha — Significance level 0.05 (default) | scalar value in the range (0,1)

Significance level of the hypothesis test, specified as the comma-separated pair consisting of 'Alpha' and a scalar value in the range (0,1).

Example: 'Alpha',0.01

Tail — Type of alternative hypothesis 'unequal' (default) | 'larger' | 'smaller'

Type of alternative hypothesis to evaluate, specified as the comma-separated pair consisting of 'Tail' and one of the following.

If the data values in x1 tend to be larger than those in x2 , the empirical distribution function of x1 tends to be smaller than that of x2 , and vice versa.

Example: 'Tail','larger'

Output Arguments

H — hypothesis test result 1 | 0.

Hypothesis test result, returned as a logical value.

If h = 1 , this indicates the rejection of the null hypothesis at the Alpha significance level.

If h = 0 , this indicates a failure to reject the null hypothesis at the Alpha significance level.

p — Asymptotic p -value scalar value in the range (0,1)

Asymptotic p -value of the test, returned as a scalar value in the range (0,1). p is the probability of observing a test statistic as extreme as, or more extreme than, the observed value under the null hypothesis. The asymptotic p -value becomes very accurate for large sample sizes, and is believed to be reasonably accurate for sample sizes n1 and n2 , such that (n1*n2)/(n1 + n2) ≥ 4 .

ks2stat — Test statistic nonnegative scalar value

Test statistic, returned as a nonnegative scalar value.

Two-Sample Kolmogorov-Smirnov Test

The two-sample Kolmogorov-Smirnov test is a nonparametric hypothesis test that evaluates the difference between the cdfs of the distributions of the two sample data vectors over the range of x in each data set.

The two-sided test uses the maximum absolute difference between the cdfs of the distributions of the two data vectors. The test statistic is

D * = max x ( | F ^ 1 ( x ) − F ^ 2 ( x ) | ) ,

where F ^ 1 ( x ) is the proportion of x1 values less than or equal to x and F ^ 2 ( x ) is the proportion of x2 values less than or equal to x .

The one-sided test uses the actual value of the difference between the cdfs of the distributions of the two data vectors rather than the absolute value. The test statistic is

D * = max x ( F ^ 1 ( x ) − F ^ 2 ( x ) ) .

In kstest2 , the decision to reject the null hypothesis is based on comparing the p -value p with the significance level Alpha , not by comparing the test statistic ks2stat with a critical value.

[1] Massey, F. J. “The Kolmogorov-Smirnov Test for Goodness of Fit.” Journal of the American Statistical Association . Vol. 46, No. 253, 1951, pp. 68–78.

[2] Miller, L. H. “Table of Percentage Points of Kolmogorov Statistics.” Journal of the American Statistical Association . Vol. 51, No. 273, 1956, pp. 111–121.

[3] Marsaglia, G., W. Tsang, and J. Wang. “Evaluating Kolmogorov’s Distribution.” Journal of Statistical Software . Vol. 8, Issue 18, 2003.

Version History

Introduced before R2006a

kstest | lillietest | adtest

MATLAB Command

You clicked a link that corresponds to this MATLAB command:

Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

• Switzerland (English)
• Switzerland (Deutsch)
• Switzerland (Français)
• 中国 (English)

You can also select a web site from the following list:

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)

Contact your local office

How Does the Null Hypothesis Work?

Last updated: June 2, 2024

• Math and Logic
• Probability and Statistics

1. Introduction

In this tutorial, we’ll explain the role of null hypotheses in standard statistical tests.

2. Statistical Tests

Let’s say we want to check how a new, recently proposed teaching method using generative AI affects students’ quiz results. To do this, we teach one class using the new AI-powered method and another using the good old presentation slides. To ensure a fair comparison, we choose the classes with equally talented students and instruct them to use the same textbook.

After scoring the quiz, we can be tempted to compute the mean scores in both classes to see which one is better. However, if we want to generalize the conclusions, we need to use statistics . The two classes we scored in this experiment are just two samples of the entire student population. So, the results might differ if the same experiment was conducted with different students. Statistical tests help us quantify this uncertainty and draw general conclusions with high confidence (if we conduct them correctly).

Usually, statistical tests have two hypotheses: the null and the alternative.

The null hypothesis is the hypothesis of “no effect,” i.e., the hypothesis opposite to the effect we want to test for. In contrast, the alternative hypothesis is the one positing the existence of the effect of interest.

3. Effects and Null Hypothesis

The effect depends on our research question. In our example, we want to check the efficacy of a new method, so we’re interested in the score difference. We must formulate the effect using quantifiable and measurable parameters to test it statistically.

3.1. The Special Role of the Null Hypothesis

3.2. the nature of scientific proofs.

The asymmetry between the null and alternative is evident in how we act depending on the test results. We’re usually interested in proving an effect. However, we behave as if that’s true only if the results are highly incompatible with the null hypothesis, as it isn’t sufficient that they are compatible with the alternative.

This means that the null acts as our default reality model , which is the one already in place or of lower risk . For instance, if we have a well-tested and very efficient teaching method, we don’t have much incentive to change it unless the new one is substantially better. Similarly, there’s more risk in erroneously recommending the use of an inefficient or harmful drug than not detecting the efficacy of an efficient one, so having a no-effect hypothesis as a default makes sense.

Therefore, we don’t need convincing to behave as if the null is true. It’s the job of the alternative hypothesis to convince us to act otherwise.

3.3. Effect Formulation

There’s more than one way to formulate the effect of interest. The choice of formulation implicitly defines assumptions about the populations. For instance, we defined the effect as a non-zero difference of means. However, the score distributions need to have the same shape for the difference in means to indicate the distributions are different:

In this case, most values likely under the new method will be unlikely under the old one, and vice versa, because the distributions have the same shape. If they don’t, different means may have little to no practical significance. So, we always have to consider our implicit assumptions and formulate the effects so that they make sense.

4. Simple vs. Composite Null

4.1. the p-value.

assuming that higher values of the test statistic are less compatible with the null.

5. Conclusion

In this article, we explained the null hypothesis in statistics. It corresponds to the no-effect state of the world. We reject it in favor of the alternative hypothesis if the observed effect is unlikely under the null.