null hypothesis equal means

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Statistics Made Easy

Two Sample t-test: Definition, Formula, and Example

A two sample t-test is used to determine whether or not two population means are equal.

This tutorial explains the following:

• The motivation for performing a two sample t-test.
• The formula to perform a two sample t-test.
• The assumptions that should be met to perform a two sample t-test.
• An example of how to perform a two sample t-test.

Two Sample t-test: Motivation

Suppose we want to know whether or not the mean weight between two different species of turtles is equal. Since there are thousands of turtles in each population, it would be too time-consuming and costly to go around and weigh each individual turtle.

Instead, we might take a simple random sample of 15 turtles from each population and use the mean weight in each sample to determine if the mean weight is equal between the two populations:

However, it’s virtually guaranteed that the mean weight between the two samples will be at least a little different. The question is whether or not this difference is statistically significant . Fortunately, a two sample t-test allows us to answer this question.

Two Sample t-test: Formula

A two-sample t-test always uses the following null hypothesis:

• H 0 : μ 1  = μ 2 (the two population means are equal)

The alternative hypothesis can be either two-tailed, left-tailed, or right-tailed:

• H 1 (two-tailed): μ 1  ≠ μ 2 (the two population means are not equal)
• H 1 (left-tailed): μ 1  < μ 2  (population 1 mean is less than population 2 mean)
• H 1 (right-tailed):  μ 1 > μ 2  (population 1 mean is greater than population 2 mean)

We use the following formula to calculate the test statistic t:

Test statistic:  ( x 1  –  x 2 )  /  s p (√ 1/n 1  + 1/n 2 )

where  x 1  and  x 2 are the sample means, n 1 and n 2  are the sample sizes, and where s p is calculated as:

s p = √  (n 1 -1)s 1 2  +  (n 2 -1)s 2 2  /  (n 1 +n 2 -2)

where s 1 2  and s 2 2  are the sample variances.

If the p-value that corresponds to the test statistic t with (n 1 +n 2 -1) degrees of freedom is less than your chosen significance level (common choices are 0.10, 0.05, and 0.01) then you can reject the null hypothesis.

Two Sample t-test: Assumptions

For the results of a two sample t-test to be valid, the following assumptions should be met:

• The observations in one sample should be independent of the observations in the other sample.
• The data should be approximately normally distributed.
• The two samples should have approximately the same variance. If this assumption is not met, you should instead perform Welch’s t-test .
• The data in both samples was obtained using a random sampling method .

Two Sample t-test : Example

Suppose we want to know whether or not the mean weight between two different species of turtles is equal. To test this, will perform a two sample t-test at significance level α = 0.05 using the following steps:

Step 1: Gather the sample data.

Suppose we collect a random sample of turtles from each population with the following information:

• Sample size n 1 = 40
• Sample mean weight  x 1  = 300
• Sample standard deviation s 1 = 18.5
• Sample size n 2 = 38
• Sample mean weight  x 2  = 305
• Sample standard deviation s 2 = 16.7

Step 2: Define the hypotheses.

We will perform the two sample t-test with the following hypotheses:

• H 0 :  μ 1  = μ 2 (the two population means are equal)
• H 1 :  μ 1  ≠ μ 2 (the two population means are not equal)

Step 3: Calculate the test statistic  t .

First, we will calculate the pooled standard deviation s p :

s p = √  (n 1 -1)s 1 2  +  (n 2 -1)s 2 2  /  (n 1 +n 2 -2)  = √  (40-1)18.5 2  +  (38-1)16.7 2  /  (40+38-2)  = 17.647

Next, we will calculate the test statistic  t :

t = ( x 1  –  x 2 )  /  s p (√ 1/n 1  + 1/n 2 ) =  (300-305) / 17.647(√ 1/40 + 1/38 ) =  -1.2508

Step 4: Calculate the p-value of the test statistic  t .

According to the T Score to P Value Calculator , the p-value associated with t = -1.2508 and degrees of freedom = n 1 +n 2 -2 = 40+38-2 = 76 is  0.21484 .

Step 5: Draw a conclusion.

Since this p-value is not less than our significance level α = 0.05, we fail to reject the null hypothesis. We do not have sufficient evidence to say that the mean weight of turtles between these two populations is different.

Note:  You can also perform this entire two sample t-test by simply using the Two Sample t-test Calculator .

Additional Resources

The following tutorials explain how to perform a two-sample t-test using different statistical programs:

How to Perform a Two Sample t-test in Excel How to Perform a Two Sample t-test in SPSS How to Perform a Two Sample t-test in Stata How to Perform a Two Sample t-test in R How to Perform a Two Sample t-test in Python How to Perform a Two Sample t-test on a TI-84 Calculator

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

2 Replies to “Two Sample t-test: Definition, Formula, and Example”

I like the detailed information and simplified in the way I can understand and relate easily. Thank you

It seems a couple of parenthesis is missed at the pooled standard deviation formula. Under square root you have (n1-1)s12 + (n2-1)s22 / (n1+n2-2) but it should be [(n1-1)s12 + (n2-1)s22] / (n1+n2-2) I used square bracket

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Hypothesis Testing with One Sample

Null and Alternative Hypotheses

OpenStaxCollege

[latexpage]

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p = 0.40
• H a : p > 0.40

<!– ??? –>

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

Chapter Review

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:

Formula Review

H 0 and H a are contradictory.

If α ≤ p -value, then do not reject H 0 .

If α > p -value, then reject H 0 .

α is preconceived. Its value is set before the hypothesis test starts. The p -value is calculated from the data.

You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. What is the random variable? Describe in words.

The random variable is the mean Internet speed in Megabits per second.

You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. State the null and alternative hypotheses.

The American family has an average of two children. What is the random variable? Describe in words.

The random variable is the mean number of children an American family has.

The mean entry level salary of an employee at a company is 💲58,000. You believe it is higher for IT professionals in the company. State the null and alternative hypotheses.

A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the proportion is actually less. What is the random variable? Describe in words.

The random variable is the proportion of people picked at random in Times Square visiting the city.

A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the claim is correct. State the null and alternative hypotheses.

In a population of fish, approximately 42% are female. A test is conducted to see if, in fact, the proportion is less. State the null and alternative hypotheses.

Suppose that a recent article stated that the mean time spent in jail by a first–time convicted burglar is 2.5 years. A study was then done to see if the mean time has increased in the new century. A random sample of 26 first-time convicted burglars in a recent year was picked. The mean length of time in jail from the survey was 3 years with a standard deviation of 1.8 years. Suppose that it is somehow known that the population standard deviation is 1.5. If you were conducting a hypothesis test to determine if the mean length of jail time has increased, what would the null and alternative hypotheses be? The distribution of the population is normal.

A random survey of 75 death row inmates revealed that the mean length of time on death row is 17.4 years with a standard deviation of 6.3 years. If you were conducting a hypothesis test to determine if the population mean time on death row could likely be 15 years, what would the null and alternative hypotheses be?

• H 0 : __________
• H a : __________
• H 0 : μ = 15
• H a : μ ≠ 15

The National Institute of Mental Health published an article stating that in any one-year period, approximately 9.5 percent of American adults suffer from depression or a depressive illness. Suppose that in a survey of 100 people in a certain town, seven of them suffered from depression or a depressive illness. If you were conducting a hypothesis test to determine if the true proportion of people in that town suffering from depression or a depressive illness is lower than the percent in the general adult American population, what would the null and alternative hypotheses be?

Some of the following statements refer to the null hypothesis, some to the alternate hypothesis.

State the null hypothesis, H 0 , and the alternative hypothesis. H a , in terms of the appropriate parameter ( μ or p ).

• The mean number of years Americans work before retiring is 34.
• At most 60% of Americans vote in presidential elections.
• The mean starting salary for San Jose State University graduates is at least 💲100,000 per year.
• Twenty-nine percent of high school seniors get drunk each month.
• Fewer than 5% of adults ride the bus to work in Los Angeles.
• The mean number of cars a person owns in her lifetime is not more than ten.
• About half of Americans prefer to live away from cities, given the choice.
• Europeans have a mean paid vacation each year of six weeks.
• The chance of developing breast cancer is under 11% for women.
• Private universities’ mean tuition cost is more than 💲20,000 per year.
• H 0 : μ = 34; H a : μ ≠ 34
• H 0 : p ≤ 0.60; H a : p > 0.60
• H 0 : μ ≥ 100,000; H a : μ < 100,000
• H 0 : p = 0.29; H a : p ≠ 0.29
• H 0 : p = 0.05; H a : p < 0.05
• H 0 : μ ≤ 10; H a : μ > 10
• H 0 : p = 0.50; H a : p ≠ 0.50
• H 0 : μ = 6; H a : μ ≠ 6
• H 0 : p ≥ 0.11; H a : p < 0.11
• H 0 : μ ≤ 20,000; H a : μ > 20,000

Over the past few decades, public health officials have examined the link between weight concerns and teen girls’ smoking. Researchers surveyed a group of 273 randomly selected teen girls living in Massachusetts (between 12 and 15 years old). After four years the girls were surveyed again. Sixty-three said they smoked to stay thin. Is there good evidence that more than thirty percent of the teen girls smoke to stay thin? The alternative hypothesis is:

• p < 0.30
• p > 0.30

A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening night midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 attended the midnight showing. An appropriate alternative hypothesis is:

• p > 0.20
• p < 0.20

Previously, an organization reported that teenagers spent 4.5 hours per week, on average, on the phone. The organization thinks that, currently, the mean is higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test. The null and alternative hypotheses are:

• H o : \(\overline{x}\) = 4.5, H a : \(\overline{x}\) > 4.5
• H o : μ ≥ 4.5, H a : μ < 4.5
• H o : μ = 4.75, H a : μ > 4.75
• H o : μ = 4.5, H a : μ > 4.5

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm.

Null and Alternative Hypotheses Copyright © 2013 by OpenStaxCollege is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 10.

• Idea behind hypothesis testing

Examples of null and alternative hypotheses

• Writing null and alternative hypotheses
• P-values and significance tests
• Comparing P-values to different significance levels
• Estimating a P-value from a simulation
• Estimating P-values from simulations
• Using P-values to make conclusions

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

16.3: The Process of Null Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 8804

• Russell A. Poldrack
• Stanford University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

We can break the process of null hypothesis testing down into a number of steps:

• Formulate a hypothesis that embodies our prediction ( before seeing the data )
• Collect some data relevant to the hypothesis
• Specify null and alternative hypotheses
• Fit a model to the data that represents the alternative hypothesis and compute a test statistic
• Compute the probability of the observed value of that statistic assuming that the null hypothesis is true
• Assess the “statistical significance” of the result

For a hands-on example, let’s use the NHANES data to ask the following question: Is physical activity related to body mass index? In the NHANES dataset, participants were asked whether they engage regularly in moderate or vigorous-intensity sports, fitness or recreational activities (stored in the variable P h y s A c t i v e PhysActive ). The researchers also measured height and weight and used them to compute the Body Mass Index (BMI):

B M I = w e i g h t ( k g ) h e i g h t ( m ) 2 BMI = \frac{weight(kg)}{height(m)^2}

16.3.1 Step 1: Formulate a hypothesis of interest

For step 1, we hypothesize that BMI is greater for people who do not engage in physical activity, compared to those who do.

16.3.2 Step 2: Collect some data

For step 2, we collect some data. In this case, we will sample 250 individuals from the NHANES dataset. Figure 16.1 shows an example of such a sample, with BMI shown separately for active and inactive individuals.

16.3.3 Step 3: Specify the null and alternative hypotheses

For step 3, we need to specify our null hypothesis (which we call H 0 H _0 ) and our alternative hypothesis (which we call H A H_A ). H 0 H _0 is the baseline against which we test our hypothesis of interest: that is, what would we expect the data to look like if there was no effect? The null hypothesis always involves some kind of equality (=, ≤ \le , or ≥ \ge ). H A H_A describes what we expect if there actually is an effect. The alternative hypothesis always involves some kind of inequality ( ≠ \ne , >, or <). Importantly, null hypothesis testing operates under the assumption that the null hypothesis is true unless the evidence shows otherwise.

We also have to decide whether to use directional or non-directional hypotheses. A non-directional hypothesis simply predicts that there will be a difference, without predicting which direction it will go. For the BMI/activity example, a non-directional null hypothesis would be:

H 0 : B M I a c t i v e = B M I i n a c t i v e H0 : BMI_{active} = BMI_{inactive}

and the corresponding non-directional alternative hypothesis would be:

H A : B M I a c t i v e ≠ B M I i n a c t i v e HA: BMI_{active} \neq BMI_{inactive}

A directional hypothesis, on the other hand, predicts which direction the difference would go. For example, we have strong prior knowledge to predict that people who engage in physical activity should weigh less than those who do not, so we would propose the following directional null hypothesis:

H 0 : B M I a c t i v e ≥ B M I i n a c t i v e H0: BMI_{active} \ge BMI_{inactive}

and directional alternative:

H A : B M I a c t i v e < B M I i n a c t i v e HA : BMI_{active} < BMI_{inactive}

As we will see later, testing a non-directional hypothesis is more conservative, so this is generally to be preferred unless there is a strong a priori reason to hypothesize an effect in a particular direction. Any direction hypotheses should be specified prior to looking at the data!

16.3.4 Step 4: Fit a model to the data and compute a test statistic

For step 4, we want to use the data to compute a statistic that will ultimately let us decide whether the null hypothesis is rejected or not. To do this, the model needs to quantify the amount of evidence in favor of the alternative hypothesis, relative to the variability in the data. Thus we can think of the test statistic as providing a measure of the size of the effect compared to the variability in the data. In general, this test statistic will have a probability distribution associated with it, because that allows us to determine how likely our observed value of the statistic is under the null hypothesis.

For the BMI example, we need a test statistic that allows us to test for a difference between two means, since the hypotheses are stated in terms of mean BMI for each group. One statistic that is often used to compare two means is the t-statistic , first developed by the statistician William Sealy Gossett, who worked for the Guiness Brewery in Dublin and wrote under the pen name “Student” - hence, it is often called “Student’s t-statistic”. The t-statistic is appropriate for comparing the means of two groups when the sample sizes are relatively small and the population standard deviation is unknown. The t-statistic for comparison of two independent groups is computed as:

t = X 1 ‾ − X 2 ‾ S 1 2 n 1 + S 2 2 n 2 t = \frac{\bar{X_1} - \bar{X_2}}{\sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}}

where X ‾ 1 \bar{X}_1 and X ‾ 2 \bar{X}_2 are the means of the two groups, S 1 2 S ^2_1 and S 2 2 S ^2_2 are the estimated variances of the groups, and n 1 n _1 and n 2 n _2 are the sizes of the two groups. Note that the denominator is basically an average of the standard error of the mean for the two samples. Thus, one can view the the t-statistic as a way of quantifying how large the difference between groups is in relation to the sampling variability of the means that are being compared.

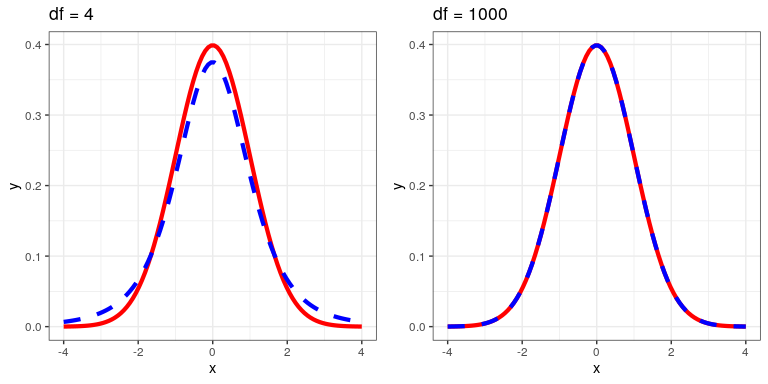
The t-statistic is distributed according to a probability distribution known as a t distribution. The t distribution looks quite similar to a normal distribution, but it differs depending on the number of degrees of freedom, which for this example is the number of observations minus 2, since we have computed two means and thus given up two degrees of freedom. When the degrees of freedom are large (say 1000), then the t distribution looks essentialy like the normal distribution, but when they are small then the t distribution has longer tails than the normal (see Figure 16.2).

16.3.5 Step 5: Determine the probability of the data under the null hypothesis

This is the step where NHST starts to violate our intuition – rather than determining the likelihood that the null hypothesis is true given the data, we instead determine the likelihood of the data under the null hypothesis - because we started out by assuming that the null hypothesis is true! To do this, we need to know the probability distribution for the statistic under the null hypothesis, so that we can ask how likely the data are under that distribution. Before we move to our BMI data, let’s start with some simpler examples.

16.3.5.1 Randomization: A very simple example

Let’s say that we wish to determine whether a coin is fair. To collect data, we flip the coin 100 times, and we count 70 heads. In this example, H 0 : P ( h e a d s ) = 0.5 H_0: P(heads)=0.5 and H A : P ( h e a d s ) ≠ 0.5 H_A: P(heads) \neq 0.5 , and our test statistic is simply the number of heads that we counted. The question that we then want to ask is: How likely is it that we would observe 70 heads if the true probability of heads is 0.5. We can imagine that this might happen very occasionally just by chance, but doesn’t seem very likely. To quantify this probability, we can use the binomial distribution :

P ( X < k ) = ∑ i = 0 k ( N k ) p i ( 1 − p ) ( n − i ) P(X < k) = \sum_{i=0}^k \binom{N}{k} p^i (1-p)^{(n-i)} This equation will tell us the likelihood of a certain number of heads or fewer, given a particular probability of heads. However, what we really want to know is the probability of a certain number or more, which we can obtain by subtracting from one, based on the rules of probability:

P ( X ≥ k ) = 1 − P ( X < k ) P(X \ge k) = 1 - P(X < k)

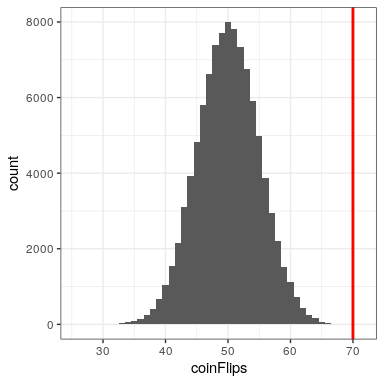
We can compute the probability for our example using the pbinom() function. The probability of 69 or fewer heads given P(heads)=0.5 is 0.999961, so the probability of 70 or more heads is simply one minus that value (0.000039) This computation shows us that the likelihood of getting 70 heads if the coin is indeed fair is very small.

Now, what if we didn’t have the pbinom() function to tell us the probability of that number of heads? We could instead determine it by simulation – we repeatedly flip a coin 100 times using a true probability of 0.5, and then compute the distribution of the number of heads across those simulation runs. Figure 16.3 shows the result from this simulation. Here we can see that the probability computed via simulation (0.000030) is very close to the theoretical probability (.00004).

Let’s do the analogous computation for our BMI example. First we compute the t statistic using the values from our sample that we calculated above, where we find that (t = 3.86). The question that we then want to ask is: What is the likelihood that we would find a t statistic of this size, if the true difference between groups is zero or less (i.e. the directional null hypothesis)?

We can use the t distribution to determine this probability. Our sample size is 250, so the appropriate t distribution has 248 degrees of freedom because lose one for each of the two means that we computed. We can use the pt() function in R to determine the probability of finding a value of the t-statistic greater than or equal to our observed value. Note that we want to know the probability of a value greater than our observed value, but by default pt() gives us the probability of a value less than the one that we provide it, so we have to tell it explicitly to provide us with the “upper tail” probability (by setting lower.tail = FALSE ). We find that (p(t > 3.86, df = 248) = 0.000), which tells us that our observed t-statistic value of 3.86 is relatively unlikely if the null hypothesis really is true.

In this case, we used a directional hypothesis, so we only had to look at one end of the null distribution. If we wanted to test a non-directional hypothesis, then we would need to be able to identify how unexpected the size of the effect is, regardless of its direction. In the context of the t-test, this means that we need to know how likely it is that the statistic would be as extreme in either the positive or negative direction. To do this, we multiply the observed t value by -1, since the t distribution is centered around zero, and then add together the two tail probabilities to get a two-tailed p-value: (p(t > 3.86 or t< -3.86, df = 248) = 0.000). Here we see that the p value for the two-tailed test is twice as large as that for the one-tailed test, which reflects the fact that an extreme value is less surprising since it could have occurred in either direction.

How do you choose whether to use a one-tailed versus a two-tailed test? The two-tailed test is always going to be more conservative, so it’s always a good bet to use that one, unless you had a very strong prior reason for using a one-tailed test. In that case, you should have written down the hypothesis before you ever looked at the data. In Chapter 32 we will discuss the idea of pre-registration of hypotheses, which formalizes the idea of writing down your hypotheses before you ever see the actual data. You should never make a decision about how to perform a hypothesis test once you have looked at the data, as this can introduce serious bias into the results.

16.3.5.2 Computing p-values using randomization

So far we have seen how we can use the t-distribution to compute the probability of the data under the null hypothesis, but we can also do this using simulation. The basic idea is that we generate simulated data like those that we would expect under the null hypothesis, and then ask how extreme the observed data are in comparison to those simulated data. The key question is: How can we generate data for which the null hypothesis is true? The general answer is that we can randomly rearrange the data in a particular way that makes the data look like they would if the null was really true. This is similar to the idea of bootstrapping, in the sense that it uses our own data to come up with an answer, but it does it in a different way.

16.3.5.3 Randomization: a simple example

Let’s start with a simple example. Let’s say that we want to compare the mean squatting ability of football players with cross-country runners, with H 0 : μ F B ≤ μ X C H_0: \mu_{FB} \le \mu_{XC} and H A : μ F B > μ X C H _A: \mu_{FB} > \mu_{XC} . We measure the maximum squatting ability of 5 football players and 5 cross-country runners (which we will generate randomly, assuming that μ F B = 300 \mu_{FB} = 300 , μ X C = 140 \mu_{XC} = 140 , and σ = 30 \sigma = 30 ).

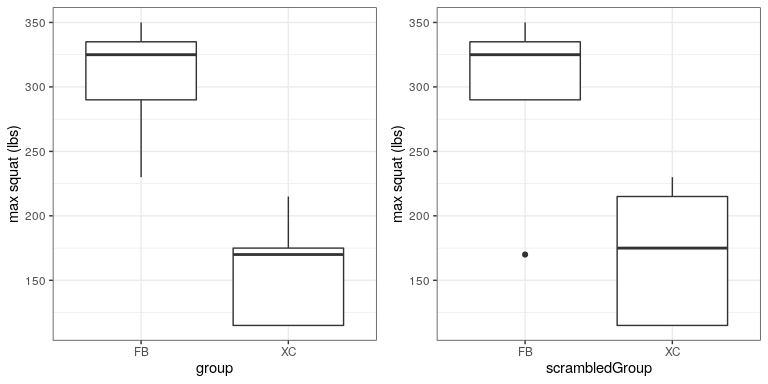
From the plot in Figure 16.4 it’s clear that there is a large difference between the two groups. We can do a standard t-test to test our hypothesis, using the t.test() command in R, which gives the following result:

If we look at the p-value reported here, we see that the likelihood of such a difference under the null hypothesis is very small, using the t distribution to define the null.

Now let’s see how we could answer the same question using randomization. The basic idea is that if the null hypothesis of no difference between groups is true, then it shouldn’t matter which group one comes from (football players versus cross-country runners) – thus, to create data that are like our actual data but also conform to the null hypothesis, we can randomly reorder the group labels for the individuals in the dataset, and then recompute the difference between the groups. The results of such a shuffle are shown in Figure ?? .

After scrambling the labels, we see that the two groups are now much more similar, and in fact the cross-country group now has a slightly higher mean. Now let’s do that 10000 times and store the t statistic for each iteration; this may take a moment to complete. Figure 16.5 shows the histogram of the t-values across all of the random shuffles. As expected under the null hypothesis, this distribution is centered at zero (the mean of the distribution is -0.016. From the figure we can also see that the distribution of t values after shuffling roughly follows the theoretical t distribution under the null hypothesis (with mean=0), showing that randomization worked to generate null data. We can compute the p-value from the randomized data by measuring how many of the shuffled values are at least as extreme as the observed value: p(t > 5.14, df = 8) using randomization = 0.00380. This p-value is very similar to the p-value that we obtained using the t distribution, and both are quite extreme, suggesting that the observed data are very unlikely to have arisen if the null hypothesis is true - and in this case we know that it’s not true, because we generated the data.

16.3.5.3.1 Randomization: BMI/activity example

Now let’s use randomization to compute the p-value for the BMI/activity example. In this case, we will randomly shuffle the PhysActive variable and compute the difference between groups after each shuffle, and then compare our observed t statistic to the distribution of t statistics from the shuffled datasets. Figure 16.6 shows the distribution of t values from the shuffled samples, and we can also compute the probability of finding a value as large or larger than the observed value. The p-value obtained from randomization (0.0000) is very similar to the one obtained using the t distribution (0.0001). The advantage of the randomization test is that it doesn’t require that we assume that the data from each of the groups are normally distributed, though the t-test is generally quite robust to violations of that assumption. In addition, the randomization test can allow us to compute p-values for statistics when we don’t have a theoretical distribution like we do for the t-test.

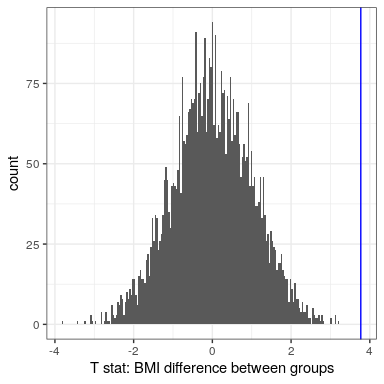
We do have to make one main assumption when we use the randomization test, which we refer to as exchangeability . This means that all of the observations are distributed in the same way, such that we can interchange them without changing the overall distribution. The main place where this can break down is when there are related observations in the data; for example, if we had data from individuals in 4 different families, then we couldn’t assume that individuals were exchangeable, because siblings would be closer to each other than they are to individuals from other families. In general, if the data were obtained by random sampling, then the assumption of exchangeability should hold.

16.3.6 Step 6: Assess the “statistical significance” of the result

The next step is to determine whether the p-value that results from the previous step is small enough that we are willing to reject the null hypothesis and conclude instead that the alternative is true. How much evidence do we require? This is one of the most controversial questions in statistics, in part because it requires a subjective judgment – there is no “correct” answer.

Historically, the most common answer to this question has been that we should reject the null hypothesis if the p-value is less than 0.05. This comes from the writings of Ronald Fisher, who has been referred to as “the single most important figure in 20th century statistics” (Efron 1998) :

“If P is between .1 and .9 there is certainly no reason to suspect the hypothesis tested. If it is below .02 it is strongly indicated that the hypothesis fails to account for the whole of the facts. We shall not often be astray if we draw a conventional line at .05 … it is convenient to draw the line at about the level at which we can say: Either there is something in the treatment, or a coincidence has occurred such as does not occur more than once in twenty trials” (Fisher 1925)

However, Fisher never intended p < 0.05 p < 0.05 to be a fixed rule:

“no scientific worker has a fixed level of significance at which from year to year, and in all circumstances, he rejects hypotheses; he rather gives his mind to each particular case in the light of his evidence and his ideas” [fish:1956]

Instead, it is likely that it became a ritual due to the reliance upon tables of p-values that were used before computing made it easy to compute p values for arbitrary values of a statistic. All of the tables had an entry for 0.05, making it easy to determine whether one’s statistic exceeded the value needed to reach that level of significance.

The choice of statistical thresholds remains deeply controversial, and recently (Benjamin et al., 2018) it has been proposed that the standard threshold be changed from .05 to .005, making it substantially more stringent and thus more difficult to reject the null hypothesis. In large part this move is due to growing concerns that the evidence obtained from a significant result at p < . 05 32.

16.3.6.1 Hypothesis testing as decision-making: The Neyman-Pearson approach

Whereas Fisher thought that the p-value could provide evidence regarding a specific hypothesis, the statisticians Jerzy Neyman and Egon Pearson disagreed vehemently. Instead, they proposed that we think of hypothesis testing in terms of its error rate in the long run:

“no test based upon a theory of probability can by itself provide any valuable evidence of the truth or falsehood of a hypothesis. But we may look at the purpose of tests from another viewpoint. Without hoping to know whether each separate hypothesis is true or false, we may search for rules to govern our behaviour with regard to them, in following which we insure that, in the long run of experience, we shall not often be wrong” (Neyman and Pearson 1933)

That is: We can’t know which specific decisions are right or wrong, but if we follow the rules, we can at least know how often our decisions will be wrong on average.

To understand the decision making framework that Neyman and Pearson developed, we first need to discuss statistical decision making in terms of the kinds of outcomes that can occur. There are two possible states of reality ( H 0 H _0 is true, or H 0 H _0 is false), and two possible decisions (reject H 0 H _0 , or fail to reject H 0 H _0 ). There are two ways in which we can make a correct decision:

• We can decide to reject H 0 H _0 when it is false (in the language of decision theory, we call this a hit )
• We can fail to reject H 0 H _0 when it is true (we call this a correct rejection )

There are also two kinds of errors we can make:

• We can decide to reject H 0 H _0 when it is actually true (we call this a false alarm , or Type I error )
• We can fail to reject H 0 H _0 when it is actually false (we call this a miss , or Type II error )

Neyman and Pearson coined two terms to describe the probability of these two types of errors in the long run:

• P(Type I error) = α \alpha
• P(Type II error) = β \beta

That is, if we set α 18.3, which is the complement of Type II error.

16.3.7 What does a significant result mean?

There is a great deal of confusion about what p-values actually mean (Gigerenzer, 2004). Let’s say that we do an experiment comparing the means between conditions, and we find a difference with a p-value of .01. There are a number of possible interpretations.

16.3.7.1 Does it mean that the probability of the null hypothesis being true is .01?

No. Remember that in null hypothesis testing, the p-value is the probability of the data given the null hypothesis ( P ( d a t a | H 0 ) P(data|H_0) ). It does not warrant conclusions about the probability of the null hypothesis given the data ( P ( H 0 | d a t a ) P(H_0|data) ). We will return to this question when we discuss Bayesian inference in a later chapter, as Bayes theorem lets us invert the conditional probability in a way that allows us to determine the latter probability.

16.3.7.2 Does it mean that the probability that you are making the wrong decision is .01?

No. This would be P ( H 0 | d a t a ) P(H_0|data) , but remember as above that p-values are probabilities of data under H 0 H _0 , not probabilities of hypotheses.

16.3.7.3 Does it mean that if you ran the study again, you would obtain the same result 99% of the time?

No. The p-value is a statement about the likelihood of a particular dataset under the null; it does not allow us to make inferences about the likelihood of future events such as replication.

16.3.7.4 Does it mean that you have found a meaningful effect?

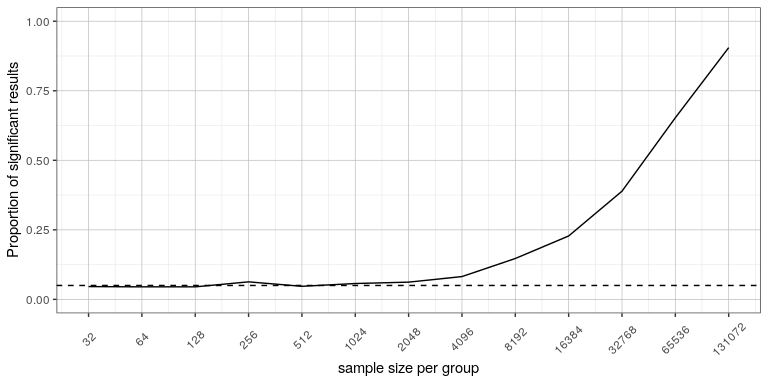
No. There is an important distinction between statistical significance and practical significance . As an example, let’s say that we performed a randomized controlled trial to examine the effect of a particular diet on body weight, and we find a statistically significant effect at p<.05. What this doesn’t tell us is how much weight was actually lost, which we refer to as the effect size (to be discussed in more detail in Chapter 18). If we think about a study of weight loss, then we probably don’t think that the loss of ten ounces (i.e. the weight of a bag of potato chips) is practically significant. Let’s look at our ability to detect a significant difference of 1 ounce as the sample size increases.

Figure 16.7 shows how the proportion of significant results increases as the sample size increases, such that with a very large sample size (about 262,000 total subjects), we will find a significant result in more than 90% of studies when there is a 1 ounce weight loss. While these are statistically significant, most physicians would not consider a weight loss of one ounce to be practically or clinically significant. We will explore this relationship in more detail when we return to the concept of statistical power in Section 18.3, but it should already be clear from this example that statistical significance is not necessarily indicative of practical significance.