Save 10% on All AnalystPrep 2024 Study Packages with Coupon Code BLOG10 .
- Payment Plans
- Product List
- Partnerships

- Try Free Trial
- Study Packages
- Levels I, II & III Lifetime Package
- Video Lessons
- Study Notes
- Practice Questions
- Levels II & III Lifetime Package
- About the Exam
- About your Instructor
- Part I Study Packages
- Part I & Part II Lifetime Package
- Part II Study Packages
- Exams P & FM Lifetime Package
- Quantitative Questions
- Verbal Questions
- Data Insight Questions
- Live Tutoring
- About your Instructors
- EA Practice Questions
- Data Sufficiency Questions
- Integrated Reasoning Questions


Hypothesis Testing in Regression Analysis
Hypothesis testing is used to confirm if the estimated regression coefficients bear any statistical significance. Either the confidence interval approach or the t-test approach can be used in hypothesis testing. In this section, we will explore the t-test approach.
The t-test Approach
The following are the steps followed in the performance of the t-test:
- Set the significance level for the test.
- Formulate the null and the alternative hypotheses.
$$t=\frac{\widehat{b_1}-b_1}{s_{\widehat{b_1}}}$$
\(b_1\) = True slope coefficient.
\(\widehat{b_1}\) = Point estimate for \(b_1\)
\(b_1 s_{\widehat{b_1\ }}\) = Standard error of the regression coefficient.
- Compare the absolute value of the t-statistic to the critical t-value (t_c). Reject the null hypothesis if the absolute value of the t-statistic is greater than the critical t-value i.e., \(t\ >\ +\ t_{critical}\ or\ t\ <\ –t_{\text{critical}}\).
Example: Hypothesis Testing of the Significance of Regression Coefficients
An analyst generates the following output from the regression analysis of inflation on unemployment:
$$\small{\begin{array}{llll}\hline{}& \textbf{Regression Statistics} &{}&{}\\ \hline{}& \text{Multiple R} & 0.8766 &{} \\ {}& \text{R Square} & 0.7684 &{} \\ {}& \text{Adjusted R Square} & 0.7394 & {}\\ {}& \text{Standard Error} & 0.0063 &{}\\ {}& \text{Observations} & 10 &{}\\ \hline {}& & & \\ \hline{} & \textbf{Coefficients} & \textbf{Standard Error} & \textbf{t-Stat}\\ \hline \text{Intercept} & 0.0710 & 0.0094 & 7.5160 \\\text{Forecast (Slope)} & -0.9041 & 0.1755 & -5.1516\\ \hline\end{array}}$$
At the 5% significant level, test the null hypothesis that the slope coefficient is significantly different from one, that is,
$$ H_{0}: b_{1} = 1\ vs. \ H_{a}: b_{1}≠1 $$
The calculated t-statistic, \(\text{t}=\frac{\widehat{b_{1}}-b_1}{\widehat{S_{b_{1}}}}\) is equal to:
$$\begin{align*}\text{t}& = \frac{-0.9041-1}{0.1755}\\& = -10.85\end{align*}$$
The critical two-tail t-values from the table with \(n-2=8\) degrees of freedom are:
$$\text{t}_{c}=±2.306$$
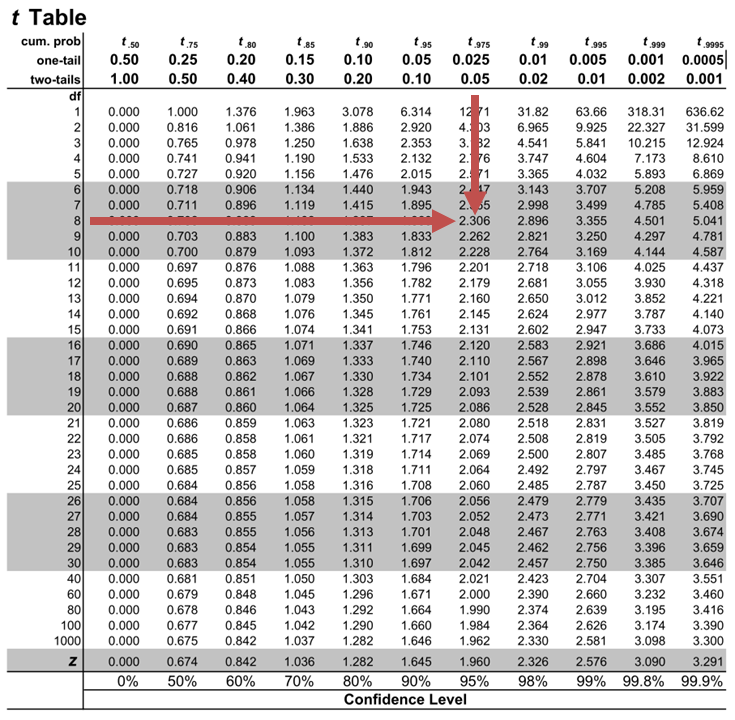
Notice that \(|t|>t_{c}\) i.e., (\(10.85>2.306\))
Therefore, we reject the null hypothesis and conclude that the estimated slope coefficient is statistically different from one.
Note that we used the confidence interval approach and arrived at the same conclusion.
Question Neeth Shinu, CFA, is forecasting price elasticity of supply for a certain product. Shinu uses the quantity of the product supplied for the past 5months as the dependent variable and the price per unit of the product as the independent variable. The regression results are shown below. $$\small{\begin{array}{lccccc}\hline \textbf{Regression Statistics} & & & & & \\ \hline \text{Multiple R} & 0.9971 & {}& {}&{}\\ \text{R Square} & 0.9941 & & & \\ \text{Adjusted R Square} & 0.9922 & & & & \\ \text{Standard Error} & 3.6515 & & & \\ \text{Observations} & 5 & & & \\ \hline {}& \textbf{Coefficients} & \textbf{Standard Error} & \textbf{t Stat} & \textbf{P-value}\\ \hline\text{Intercept} & -159 & 10.520 & (15.114) & 0.001\\ \text{Slope} & 0.26 & 0.012 & 22.517 & 0.000\\ \hline\end{array}}$$ Which of the following most likely reports the correct value of the t-statistic for the slope and most accurately evaluates its statistical significance with 95% confidence? A. \(t=21.67\); slope is significantly different from zero. B. \(t= 3.18\); slope is significantly different from zero. C. \(t=22.57\); slope is not significantly different from zero. Solution The correct answer is A . The t-statistic is calculated using the formula: $$\text{t}=\frac{\widehat{b_{1}}-b_1}{\widehat{S_{b_{1}}}}$$ Where: \(b_{1}\) = True slope coefficient \(\widehat{b_{1}}\) = Point estimator for \(b_{1}\) \(\widehat{S_{b_{1}}}\) = Standard error of the regression coefficient $$\begin{align*}\text{t}&=\frac{0.26-0}{0.012}\\&=21.67\end{align*}$$ The critical two-tail t-values from the t-table with \(n-2 = 3\) degrees of freedom are: $$t_{c}=±3.18$$ Notice that \(|t|>t_{c}\) (i.e \(21.67>3.18\)). Therefore, the null hypothesis can be rejected. Further, we can conclude that the estimated slope coefficient is statistically different from zero.
Offered by AnalystPrep


Analysis of Variance (ANOVA)
Predicted value of a dependent variable, application of probability rules.
Probability rules are the concepts and facts that must be taken into account... Read More
Yield Conversions
Yield conversion is basically the process of changing from one type of yield... Read More
Continuous Compounding
Continuous compounding applies either when the frequency with which we calculate interest is... Read More
Point Estimate vs. Confidence Interval ...
Point Estimate A point estimate gives statisticians a single value as the estimate... Read More

IMAGES
VIDEO