hypothesis for sample means

Module 10: Inference for Means

Hypothesis test for a population mean (1 of 5), learning outcomes.

• Recognize when to use a hypothesis test or a confidence interval to draw a conclusion about a population mean.
• Under appropriate conditions, conduct a hypothesis test about a population mean. State a conclusion in context.

Introduction

In Inference for Means , our focus is on inference when the variable is quantitative, so the parameters and statistics are means. In “Estimating a Population Mean,” we learned how to use a sample mean to calculate a confidence interval. The confidence interval estimates a population mean. In “Hypothesis Test for a Population Mean,” we learn to use a sample mean to test a hypothesis about a population mean.

We did hypothesis tests in earlier modules. In Inference for One Proportion , each claim involved a single population proportion. In Inference for Two Proportions , the claim was a statement about a treatment effect or a difference in population proportions. In “Hypothesis Test for a Population Mean,” the claims are statements about a population mean. But we will see that the steps and the logic of the hypothesis test are the same. Before we get into the details, let’s practice identifying research questions and studies that involve a population mean.

Cell Phone Data

Cell phones and cell phone plans can be very expensive, so consumers must think carefully when choosing a cell phone and service. This decision is as much about choosing the right cellular company as it is about choosing the right phone. Many people use the data/Internet capabilities of a phone as much as, if not more than, they use voice capability. The data service of a cell company is therefore an important factor in this decision. In the following example, a student named Melanie from Los Angeles applies what she learned in her statistics class to help her make a decision about buying a data plan for her smartphone.

Melanie read an advertisement from the Cell Phone Giants (CPG, for short, and yes, we’re using a fictitious company name) that she thinks is too good to be true. The CPG ad states that customers in Los Angeles get average data download speeds of 4 Mbps. With this speed, the ad claims, it takes, on average, only 12 seconds to download a typical 3-minute song from iTunes.

Only 12 seconds on average to download a 3-minute song from iTunes! Melanie has her doubts about this claim, so she gathers data to test it. She asks a friend who uses the CPG plan to download a song, and it takes 13 seconds to download a 3-minute song using the CPG network. Melanie decides to gather more evidence. She uses her friend’s phone and times the download of the same 3-minute song from various locations in Los Angeles. She gets a mean download time of 13.5 seconds for her sample of downloads.

What can Melanie conclude? Her sample has a mean download time that is greater than 12 seconds. Isn’t this evidence that the CPG claim is wrong? Why is a hypothesis test necessary? Isn’t the conclusion clear?

Let’s review the reason Melanie needs to do a hypothesis test before she can reach a conclusion.

Why should Melanie do a hypothesis test?

Melanie’s data (with a mean of 13.5 seconds) suggest that the average download time overall is greater than the 12 seconds claimed by the manufacturer. But wait. We know that samples will vary. If the CPG claim is correct, we don’t expect all samples to have a mean download time exactly equal to 12 seconds. There will be variability in the sample means. But if the overall average download time is 12 seconds, how much variability in sample means do we expect to see? We need to determine if the difference Melanie observed can be explained by chance.

We have to judge Melanie’s data against random samples that come from a population with a mean of 12. For this reason, we must do a simulation or use a mathematical model to examine the sampling distribution of sample means. Based on the sampling distribution, we ask, Is it likely that the samples will have mean download times that are greater than 13.5 seconds if the overall mean is 12 seconds? This probability (the P-value) determines whether Melanie’s data provides convincing evidence against the CPG claim.

Now let’s do the hypothesis test.

Step 1: Determine the hypotheses.

As always, hypotheses come from the research question. The null hypothesis is a hypothesis that the population mean equals a specific value. The alternative hypothesis reflects our claim. The alternative hypothesis says the population mean is “greater than” or “less than” or “not equal to” the value we assume is true in the null hypothesis.

Melanie’s hypotheses:

• H 0 : It takes 12 seconds on average to download Melanie’s song from iTunes with the CPG network in Los Angeles.
• H a : It takes more than 12 seconds on average to download Melanie’s song from iTunes using the CPG network in Los Angeles.

We can write the hypotheses in terms of µ. When we do so, we should always define µ. Here μ = the average number of seconds it takes to download Melanie’s song on the CPG network in Los Angeles.

• H 0 : μ = 12
• H a : μ > 12

Step 2: Collect the data.

To conduct a hypothesis test, Melanie knows she has to use a t-model of the sampling distribution. She thinks ahead to the conditions required, which helps her collect a useful sample.

Recall the conditions for use of a t-model.

• There is no reason to think the download times are normally distributed (they might be, but this isn’t something Melanie could know for sure). So the sample has to be large (more than 30).
• The sample has to be random. Melanie decides to use one phone but randomly selects days, times, and locations in Los Angeles.

Melanie collects a random sample of 45 downloads by using her friend’s phone to download her song from iTunes according to the randomly selected days, times, and locations.

Melanie’s sample of size 45 downloads has an average download time of 13.5 seconds. The standard deviation for the sample is 3.2 seconds. Now Melanie needs to determine how unlikely this data is if CPG’s claim is actually true.

Step 3: Assess the evidence.

Assuming the average download time for Melanie’s song is really 12 seconds, what is the probability that 45 random downloads of this song will have a mean of 13.5 seconds or more?

This is a question about sampling variability. Melanie must determine the standard error. She knows the standard error of random sample means is [latex]\sigma \text{}/\sqrt{n}[/latex]. Since she has no way of knowing the population standard deviation, σ, Melanie uses the sample standard deviation, s = 3.2, as an approximation. Therefore, Melanie approximates the standard error of all sample means ( n = 45) to be

[latex]s\text{}/\sqrt{n}\text{}=\text{}3.2\text{}/\sqrt{45}\text{}=\text{}0.48[/latex]

Now she can assess how far away her sample is from the claimed mean in terms of standard errors. That is, she can compute the t-score of her sample mean.

[latex]T\text{}=\text{}\frac{\mathrm{statistic}-\mathrm{parameter}}{\mathrm{standard}\text{}\mathrm{error}}\text{}=\text{}\frac{\stackrel{¯}{x}-μ}{s\text{}/\sqrt{n}}\text{}=\text{}\frac{13.5-12}{0.48}\text{}=\text{}3.14[/latex]

The sample mean for Melanie’s random sample is approximately 3.14 standard errors above the overall mean of 12. We know from previous experience that a sample mean this far above µ is very unlikely. With a t-score this large, the P-value is very small. We use a simulation of the t-model for 44 degrees of freedom to verify this.

We want the probability that the sample mean is greater than 13.5. This corresponds to the probability that T is greater than 3.14. The P-value is 0.0015.

Step 4: State a conclusion.

Here the logic is the same as for other hypothesis tests. We use the P-value to make a decision. The P-value helps us determine if the difference we see between the data and the hypothesized value of µ is statistically significant or due to chance. One of two outcomes can occur:

• One possibility is that results similar to the actual sample are extremely unlikely. This means the data does not fit with results from random samples selected from the population described by the null hypothesis. In this case, it is unlikely that the data came from this population. The probability as measured by the P-value is small, so we view this as strong evidence against the null hypothesis. We reject the null hypothesis in favor of the alternative hypothesis.
• The other possibility is that results similar to the actual sample are fairly likely (not unusual). This means the data fits with typical results from random samples selected from the population described by the null hypothesis. The probability as measured by the P-value is large. In this case, we do not have evidence against the null hypothesis, so we cannot reject it in favor of the alternative hypothesis.

Melanie’s data is very unlikely if µ = 12. The probability is essentially zero (P-value = 0.0015). This means we will rarely see sample means greater than 13.5 if µ = 12. So we reject the null and accept the alternative hypothesis. In other words, this sample provides strong evidence that CPG has overstated the speed of its data download capability.

The following activities give you an opportunity to practice parts of the hypothesis testing process for a population mean. Later you will have the opportunity to practice the hypothesis test from start to finish.

For the following scenarios, give the null and alternative hypotheses and state in words what µ represents in your hypotheses. A good definition of µ describes both the variable and the population.

In the previous example, Melanie did not state a significance level for her test. If she had, the logic is the same as we used for hypothesis tests in Modules 8 and 9. To come to a conclusion about H 0 , we compare the P-value to the significance level α.

• If P ≤ α, we reject H 0 . We conclude there is significant evidence in favor of H a .
• If P > α, we fail to reject H 0 . We conclude the sample does not provide significant evidence in favor of H a .

Use this simulation when needed to answer questions below.

Contribute!

Improve this page Learn More

• Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

• FOR INSTRUCTOR
• FOR INSTRUCTORS

8.4.3 Hypothesis Testing for the Mean

$\quad$ $H_0$: $\mu=\mu_0$, $\quad$ $H_1$: $\mu \neq \mu_0$.

$\quad$ $H_0$: $\mu \leq \mu_0$, $\quad$ $H_1$: $\mu > \mu_0$.

$\quad$ $H_0$: $\mu \geq \mu_0$, $\quad$ $H_1$: $\mu \lt \mu_0$.

Two-sided Tests for the Mean:

Therefore, we can suggest the following test. Choose a threshold, and call it $c$. If $|W| \leq c$, accept $H_0$, and if $|W|>c$, accept $H_1$. How do we choose $c$? If $\alpha$ is the required significance level, we must have

• As discussed above, we let \begin{align}%\label{} W(X_1,X_2, \cdots,X_n)=\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}. \end{align} Note that, assuming $H_0$, $W \sim N(0,1)$. We will choose a threshold, $c$. If $|W| \leq c$, we accept $H_0$, and if $|W|>c$, accept $H_1$. To choose $c$, we let \begin{align} P(|W| > c \; | \; H_0) =\alpha. \end{align} Since the standard normal PDF is symmetric around $0$, we have \begin{align} P(|W| > c \; | \; H_0) = 2 P(W>c | \; H_0). \end{align} Thus, we conclude $P(W>c | \; H_0)=\frac{\alpha}{2}$. Therefore, \begin{align} c=z_{\frac{\alpha}{2}}. \end{align} Therefore, we accept $H_0$ if \begin{align} \left|\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \right| \leq z_{\frac{\alpha}{2}}, \end{align} and reject it otherwise.
• We have \begin{align} \beta (\mu) &=P(\textrm{type II error}) = P(\textrm{accept }H_0 \; | \; \mu) \\ &= P\left(\left|\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \right| \lt z_{\frac{\alpha}{2}}\; | \; \mu \right). \end{align} If $X_i \sim N(\mu,\sigma^2)$, then $\overline{X} \sim N(\mu, \frac{\sigma^2}{n})$. Thus, \begin{align} \beta (\mu)&=P\left(\left|\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \right| \lt z_{\frac{\alpha}{2}}\; | \; \mu \right)\\ &=P\left(\mu_0- z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}} \leq \overline{X} \leq \mu_0+ z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\right)\\ &=\Phi\left(z_{\frac{\alpha}{2}}+\frac{\mu_0-\mu}{\sigma / \sqrt{n}}\right)-\Phi\left(-z_{\frac{\alpha}{2}}+\frac{\mu_0-\mu}{\sigma / \sqrt{n}}\right). \end{align}
• Let $S^2$ be the sample variance for this random sample. Then, the random variable $W$ defined as \begin{equation} W(X_1,X_2, \cdots, X_n)=\frac{\overline{X}-\mu_0}{S / \sqrt{n}} \end{equation} has a $t$-distribution with $n-1$ degrees of freedom, i.e., $W \sim T(n-1)$. Thus, we can repeat the analysis of Example 8.24 here. The only difference is that we need to replace $\sigma$ by $S$ and $z_{\frac{\alpha}{2}}$ by $t_{\frac{\alpha}{2},n-1}$. Therefore, we accept $H_0$ if \begin{align} |W| \leq t_{\frac{\alpha}{2},n-1}, \end{align} and reject it otherwise. Let us look at a numerical example of this case.

$\quad$ $H_0$: $\mu=170$, $\quad$ $H_1$: $\mu \neq 170$.

• Let's first compute the sample mean and the sample standard deviation. The sample mean is \begin{align}%\label{} \overline{X}&=\frac{X_1+X_2+X_3+X_4+X_5+X_6+X_7+X_8+X_9}{9}\\ &=165.8 \end{align} The sample variance is given by \begin{align}%\label{} {S}^2=\frac{1}{9-1} \sum_{k=1}^9 (X_k-\overline{X})^2&=68.01 \end{align} The sample standard deviation is given by \begin{align}%\label{} S&= \sqrt{S^2}=8.25 \end{align} The following MATLAB code can be used to obtain these values: x=[176.2,157.9,160.1,180.9,165.1,167.2,162.9,155.7,166.2]; m=mean(x); v=var(x); s=std(x); Now, our test statistic is \begin{align} W(X_1,X_2, \cdots, X_9)&=\frac{\overline{X}-\mu_0}{S / \sqrt{n}}\\ &=\frac{165.8-170}{8.25 / 3}=-1.52 \end{align} Thus, $|W|=1.52$. Also, we have \begin{align} t_{\frac{\alpha}{2},n-1} = t_{0.025,8} \approx 2.31 \end{align} The above value can be obtained in MATLAB using the command $\mathtt{tinv(0.975,8)}$. Thus, we conclude \begin{align} |W| \leq t_{\frac{\alpha}{2},n-1}. \end{align} Therefore, we accept $H_0$. In other words, we do not have enough evidence to conclude that the average height in the city is different from the average height in the country.

Let us summarize what we have obtained for the two-sided test for the mean.

One-sided Tests for the Mean:

• As before, we define the test statistic as \begin{align}%\label{} W(X_1,X_2, \cdots,X_n)=\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}. \end{align} If $H_0$ is true (i.e., $\mu \leq \mu_0$), we expect $\overline{X}$ (and thus $W$) to be relatively small, while if $H_1$ is true, we expect $\overline{X}$ (and thus $W$) to be larger. This suggests the following test: Choose a threshold, and call it $c$. If $W \leq c$, accept $H_0$, and if $W>c$, accept $H_1$. How do we choose $c$? If $\alpha$ is the required significance level, we must have \begin{align} P(\textrm{type I error}) &= P(\textrm{Reject }H_0 \; | \; H_0) \\ &= P(W > c \; | \; \mu \leq \mu_0) \leq \alpha. \end{align} Here, the probability of type I error depends on $\mu$. More specifically, for any $\mu \leq \mu_0$, we can write \begin{align} P(\textrm{type I error} \; | \; \mu) &= P(\textrm{Reject }H_0 \; | \; \mu) \\ &= P(W > c \; | \; \mu)\\ &=P \left(\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}> c \; | \; \mu\right)\\ &=P \left(\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}+\frac{\mu-\mu_0}{\sigma / \sqrt{n}}> c \; | \; \mu\right)\\ &=P \left(\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}> c+\frac{\mu_0-\mu}{\sigma / \sqrt{n}} \; | \; \mu\right)\\ &\leq P \left(\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}> c \; | \; \mu\right) \quad (\textrm{ since }\mu \leq \mu_0)\\ &=1-\Phi(c) \quad \big(\textrm{ since given }\mu, \frac{\overline{X}-\mu}{\sigma / \sqrt{n}} \sim N(0,1) \big). \end{align} Thus, we can choose $\alpha=1-\Phi(c)$, which results in \begin{align} c=z_{\alpha}. \end{align} Therefore, we accept $H_0$ if \begin{align} \frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \leq z_{\alpha}, \end{align} and reject it otherwise.

$\quad$ $H_0$: $\mu \geq \mu_0$, $\quad$ $H_1$: $\mu \lt \mu_0$,

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

8.2.3.1 - one sample mean t test, formulas, five step hypothesis testing procedure.

Data must be quantitative. In order to use the t distribution to approximate the sampling distribution either the sample size must be large (\(\ge\ 30\)) or the population must be known to be normally distributed. The possible combinations of null and alternative hypotheses are:

where \( \mu_{0} \) is the hypothesized population mean.

For the test of one group mean we will be using a \(t\) test statistic:

\(t=\dfrac{\overline{x}-\mu_0}{\frac{s}{\sqrt{n}}}\)

\(\overline{x}\) = sample mean \(\mu_{0}\) = hypothesized population mean \(s\) = sample standard deviation \(n\) = sample size

Note that structure of this formula is similar to the general formula for a test statistic:

\(\dfrac{sample\;statistic-null\;value}{standard\;error}\)

When testing hypotheses about a mean or mean difference, a \(t\) distribution is used to find the \(p\)-value. These \(t\) distributions are indexed by a quantity called degrees of freedom, calculated as \(df = n – 1\) for the situation involving a test of one mean or test of mean difference. The \(p\)-value can be found using Minitab.

If \(p \leq \alpha\) reject the null hypothesis.

If \(p>\alpha\) fail to reject the null hypothesis.

Based on your decision in Step 4, write a conclusion in terms of the original research question.

The new few pages will walk you through examples before giving you the opportunity to do two on your own.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

8.6 Hypothesis Tests for a Population Mean with Known Population Standard Deviation

Learning objectives.

• Conduct and interpret hypothesis tests for a population mean with known population standard deviation.

Some notes about conducting a hypothesis test:

• The null hypothesis [latex]H_0[/latex] is always an “equal to.”  The null hypothesis is the original claim about the population parameter.
• The alternative hypothesis [latex]H_a[/latex] is a “less than,” “greater than,” or “not equal to.”  The form of the alternative hypothesis depends on the context of the question.
• If the alternative hypothesis is a “less than”, then the test is left-tail.  The p -value is the area in the left-tail of the distribution.
• If the alternative hypothesis is a “greater than”, then the test is right-tail.  The p -value is the area in the right-tail of the distribution.
• If the alternative hypothesis is a “not equal to”, then the test is two-tail.  The p -value is the sum of the area in the two-tails of the distribution.  Each tail represents exactly half of the p -value.
• Think about the meaning of the p -value.  A data analyst (and anyone else) should have more confidence that they made the correct decision to reject the null hypothesis with a smaller p -value (for example, 0.001 as opposed to 0.04) even if using a significance level of 0.05.  Similarly, for a large p -value such as 0.4, as opposed to a p -value of 0.056 (a significance level of 0.05 is less than either number), a data analyst should have more confidence that they made the correct decision in not rejecting the null hypothesis.  This makes the data analyst use judgment rather than mindlessly applying rules.
• The significance level must be identified before collecting the sample data and conducting the test.  Generally, the significance level will be included in the question.  If no significance level is given, a common standard is to use a significance level of 5%.
• An alternative approach for hypothesis testing is to use what is called the critical value approach .  In this book, we will only use the p -value approach.  Some of the videos below may mention the critical value approach, but this approach will not be used in this book.

Suppose the hypotheses for a hypothesis test are:

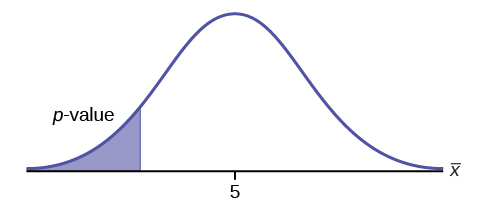
[latex]\begin{eqnarray*} H_0: & & \mu=5 \\ H_a: & & \mu \lt 5 \end{eqnarray*}[/latex]

Because the alternative hypothesis is a [latex]\lt[/latex], this is a left-tailed test.  The p -value is the area in the left-tail of the distribution.

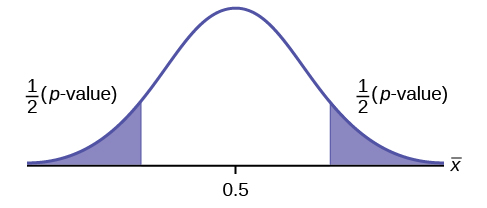
[latex]\begin{eqnarray*} H_0: & & \mu=0.5 \\ H_a: & & \mu \neq 0.5  \end{eqnarray*}[/latex]

Because the alternative hypothesis is a [latex]\neq[/latex], this is a two-tailed test.  The p -value is the sum of the areas in the two tails of the distribution.  Each tail contains exactly half of the p -value.

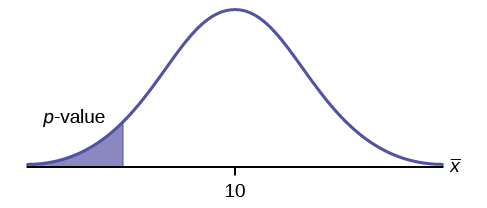
[latex]\begin{eqnarray*} H_0: & & \mu=10 \\ H_a: & & \mu \lt 10  \end{eqnarray*}[/latex]

Steps to Conduct a Hypothesis Test for a Population Mean with Known Population Standard Deviation

• Write down the null and alternative hypotheses in terms of the population mean [latex]\mu[/latex].  Include appropriate units with the values of the mean.
• Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
• Collect the sample information for the test and identify the significance level [latex]\alpha[/latex].
• When the population standard deviation is known , we use a normal distribution with [latex]\displaystyle{z=\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}}[/latex] to find the p -value.  The p -value is the area in the corresponding tail of the normal distribution.
• The results of the sample data are significant.  There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
• The results of the sample data are not significant.  There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
• Write down a concluding sentence specific to the context of the question.

USING EXCEL TO CALCULE THE P -VALUE FOR A HYPOTHESIS TEST ON A POPULATION MEAN WITH KNOWN POPULATION STANDARD DEVIATION

The p -value for a hypothesis test on a population mean is the area in the tail(s) of the distribution of the sample mean.  When the population standard deviation is known, use the normal distribution to find the p -value.

The p -value is the area in the tail(s) of a normal distribution, so the norm.dist(x,[latex]\mu[/latex],[latex]\sigma[/latex],logic operator) function can be used to calculate the p -value.

• For x , enter the value for [latex]\overline{x}[/latex].
• For [latex]\mu[/latex] , enter the mean of the sample means [latex]\mu[/latex].  Note:  Because the test is run assuming the null hypothesis is true, the value for [latex]\mu[/latex] is the claim from the null hypothesis.
• For [latex]\sigma[/latex] , enter the standard error of the mean [latex]\displaystyle{\frac{\sigma}{\sqrt{n}}}[/latex].
• For the logic operator , enter true .  Note:  Because we are calculating the area under the curve, we always enter true for the logic operator.

Use the appropriate technique with the norm.dist function to find the area in the left-tail or the area in the right-tail.

Jeffrey, as an eight-year old, established a mean time of 16.43 seconds with a standard deviation of 0.8 seconds for swimming the 25-meter freestyle.  His dad, Frank, thought that Jeffrey could swim the 25-meter freestyle faster using goggles.  Frank bought Jeffrey a new pair of goggles and timed Jeffrey swimming the 25-meter freestyle 15 different times.  In the sample of 15 swims, Jeffrey’s mean time was 16 seconds.  Frank thought that the goggles helped Jeffrey swim faster than 16.43 seconds.  At the 5% significance level, did Jeffrey swim faster wearing the goggles?  Assume that the swim times for the 25-meter freestyle are normally distributed.

Hypotheses:

[latex]\begin{eqnarray*} H_0: & & \mu=16.43 \mbox{ seconds} \\ H_a: & & \mu \lt 16.43 \mbox{ seconds} \end{eqnarray*}[/latex]

From the question, we have [latex]n=15[/latex], [latex]\overline{x}=16[/latex], [latex]\sigma=0.8[/latex] and [latex]\alpha=0.05[/latex].

This is a test on a population mean where the population standard deviation is known ([latex]\sigma=0.8[/latex]).  So we use a normal distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\lt[/latex], the p -value is the area in the left-tail of the distribution.

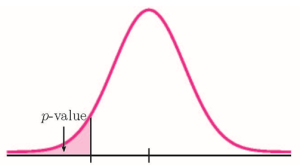
So the p -value[latex]=0.0187[/latex].

Conclusion:

Because p -value[latex]=0.0187 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis.  At the 5% significance level there is enough evidence to suggest that Jeffrey’s mean swim time with the goggles is less than 16.43 seconds.

• The null hypothesis [latex]\mu=16.43[/latex] is the claim that Jeffrey’s mean swim time with the goggles is 16.43 seconds (the same as it is without the googles).
• The alternative hypothesis [latex]\mu \lt 16.43[/latex] is the claim that Jeffrey’s swim time with the goggles is less than 16.43 seconds.
• The function is norm.dist because we are finding the area in the left tail of a normal distribution.
• Field 1 is the value of [latex]\overline{x}[/latex]
• Field 2 is the value of [latex]\mu[/latex] from the null hypothesis.  Remember, we run the test assuming the null hypothesis is true, so that means we assume [latex]\mu=16.43[/latex].
• Field 3 is the standard deviation for the sample means [latex]\displaystyle{\frac{\sigma}{\sqrt{n}}}[/latex].  Note that we are not using the standard deviation from the population ([latex]\sigma=0.8[/latex]).  This is because the p -value is the area under the curve of the distribution of the sample means, not the distribution of the population.
• The p -value of 0.0187 tells us that under the assumption that Jeffrey’s mean swim time with goggles is 16.43 seconds (the null hypothesis), there is only a 1.87% chance that the mean time for the 15 sample swims is 16 seconds or less.  This is a small probability, and so is unlikely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis.
• The Type I error for this problem is to conclude that Jeffrey swims the 25-meter freestyle, on average, in less than 16.43 seconds (the alternative hypothesis) when, in fact, he actually swims the 25-meter freestyle, on average, in 16.43 seconds (the null hypothesis).  That is, reject the null hypothesis when the null hypothesis is actually true.
• The Type II error for this problem is to conclude that Jeffrey swims the 25-meter freestyle, on average, in 16.43 seconds (the null hypothesis) when, in fact, he actually swims the 25-meter freestyle, on average, in less than 16.43 seconds (the alternative hypothesis).  That is, do not reject the null hypothesis when the null hypothesis is actually false.

The mean throwing distance of a football for Marco, a high school freshman quarterback, is 40 yards with a standard deviation of 2 yards.  The team coach tells Marco to adjust his grip to get more distance.  The coach records the distances for 20 throws with the new grip.  For the 20 throws, Marco’s mean distance was 41.5 yards.  The coach thought the different grip helped Marco throw farther than 40 yards.  At the 5% significance level, is Marco’s mean throwing distance higher with the new grip?  Assume the throw distances for footballs are normally distributed.

[latex]\begin{eqnarray*} H_0: & & \mu=40 \mbox{ yards} \\ H_a: & & \mu \gt 40 \mbox{ yards} \end{eqnarray*}[/latex]

From the question, we have [latex]n=20[/latex], [latex]\overline{x}=41.5[/latex], [latex]\sigma=2[/latex] and [latex]\alpha=0.05[/latex].

This is a test on a population mean where the population standard deviation is known ([latex]\sigma=2[/latex]).  So we use a normal distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the area in the right-tail of the distribution.

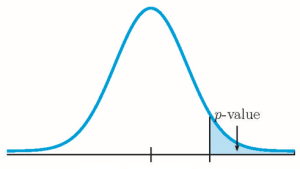
So the p -value[latex]=0.0004[/latex].

Because p -value[latex]=0.0004 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis.  At the 5% significance level there is enough evidence to suggest that Marco’s mean throwing distance is greater than 40 yards with the new grip.

• The null hypothesis [latex]\mu=40[/latex] is the claim that Marco’s mean throwing distance with the new grip is 40 yards (the same as it is without the new grip).
• The alternative hypothesis [latex]\mu \gt 40[/latex] is the claim that Marco’s mean throwing distance with the new grip is greater than 40 yards.
• Field 2 is the value of [latex]\mu[/latex] from the null hypothesis.
• Field 3 is the standard deviation for the sample means [latex]\displaystyle{\frac{\sigma}{\sqrt{n}}}[/latex].
• The p -value of 0.0004 tells us that under the assumption that Marco’s mean throwing distance with the new grip is 40 yards, there is only a 0.047% chance that the mean throwing distance for the 20 sample throws is more than 40 yards.  This is a small probability, and so is unlikely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis.

A local college states in its marketing materials that the average age of its first-year students is 18.3 years with a standard deviation of 3.4 years.  But this information is based on old data and does not take into account that more older adults are returning to college.  A researcher at the college believes that the average age of its first-year students has changed.  The researcher takes a sample of 50 first-year students and finds the average age is 19.5 years.  At the 1% significance level, has the average age of the college’s first-year students changed?

[latex]\begin{eqnarray*} H_0: & & \mu=18.3 \mbox{ years} \\ H_a: & & \mu \neq 18.3 \mbox{ years} \end{eqnarray*}[/latex]

From the question, we have [latex]n=50[/latex], [latex]\overline{x}=19.5[/latex], [latex]\sigma=3.4[/latex] and [latex]\alpha=0.01[/latex].

This is a test on a population mean where the population standard deviation is known ([latex]\sigma=3.4[/latex]).  In this case, the sample size is greater than 30.  So we use a normal distribution to calculate the p -value.  Because the alternative hypothesis is a [latex]\neq[/latex], the p -value is the sum of area in the tails of the distribution.

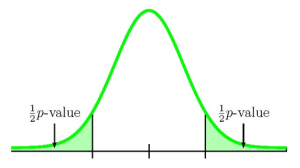
Because there is only one sample, we only have information relating to one of the two tails, either the left tail or the right tail.  We need to know if the sample relates to the left tail or right tail because that will determine how we calculate out the area of that tail using the normal distribution.  In this case, the sample mean [latex]\overline{x}=19.5[/latex] is greater than the value of the population mean in the null hypothesis [latex]\mu=18.3[/latex] ([latex]\overline{x}=19.5>18.3=\mu[/latex]), so the sample information relates to the right-tail of the normal distribution.  This means that we will calculate out the area in the right tail using 1-norm.dist .  However, this is a two-tailed test where the p -value is the sum of the area in the two tails and the area in the right-tail is only one half of the p -value.  The area in the left tail equals the area in the right tail and the p -value is the sum of these two areas.

So the area in the right tail is 0.0063 and [latex]\frac{1}{2}[/latex]( p -value)[latex]=0.0063[/latex].  This is also the area in the left tail, so

p -value[latex]=0.0063+0.0063=0.0126[/latex]

Because p -value[latex]=0.0126 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis.  At the 1% significance level there is not enough evidence to suggest that the average age of the college’s first-year students has changed.

• The null hypothesis [latex]\mu=18.3[/latex] is the claim that the average age of the first-year students is still 18.3 years.
• The alternative hypothesis [latex]\mu \neq 18.3[/latex] is the claim that the average age of the first-year students has changed from 18.3 years.
• We use norm.dist([latex]\overline{x}[/latex],[latex]\mu[/latex],[latex]\sigma/\mbox{sqrt}(n)[/latex],true) to find the area in the left tail.  The area in the right tail equals the area in the left tail, so we can find the p -value by adding the output from this function to itself.
• We use 1-norm.dist([latex]\overline{x}[/latex],[latex]\mu[/latex],[latex]\sigma/\mbox{sqrt}(n)[/latex],true) to find the area in the right tail.  The area in the left tail equals the area in the right tail, so we can find the p -value by adding the output from this function to itself.
• The p -value of 0.0126  is a large probability compared to the 1% significance level, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the claim that the average age of first-year students is 18.3 years is most likely correct.

Watch this video: Hypothesis Testing: z -test, right tail by ExcelIsFun [33:47]

Watch this video: Hypothesis Testing: z -test, left tail by ExcelIsFun [10:57]

Watch this video: Hypothesis Testing: z -test, two tail by ExcelIsFun [9:56]

Concept Review

The hypothesis test for a population mean is a well established process:

• Collect the sample information for the test and identify the significance level.
• When the population standard deviation is known, find the p -value (the area in the corresponding tail) for the test using the normal distribution.
• Compare the p -value to the significance level and state the outcome of the test.

Attribution

“ 9.6   Hypothesis Testing of a Single Mean and Single Proportion “ in Introductory Statistics by OpenStax  is licensed under a  Creative Commons Attribution 4.0 International License.

Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Teach yourself statistics

Hypothesis Test: Difference Between Means

This lesson explains how to conduct a hypothesis test for the difference between two means. The test procedure, called the two-sample t-test , is appropriate when the following conditions are met:

• The sampling method for each sample is simple random sampling .
• The samples are independent .
• Each population is at least 20 times larger than its respective sample .
• The population distribution is normal.
• The population data are symmetric , unimodal , without outliers , and the sample size is 15 or less.
• The population data are slightly skewed , unimodal, without outliers, and the sample size is 16 to 40.
• The sample size is greater than 40, without outliers.

This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.

The table below shows three sets of null and alternative hypotheses. Each makes a statement about the difference d between the mean of one population μ 1 and the mean of another population μ 2 . (In the table, the symbol ≠ means " not equal to ".)

The first set of hypotheses (Set 1) is an example of a two-tailed test , since an extreme value on either side of the sampling distribution would cause a researcher to reject the null hypothesis. The other two sets of hypotheses (Sets 2 and 3) are one-tailed tests , since an extreme value on only one side of the sampling distribution would cause a researcher to reject the null hypothesis.

When the null hypothesis states that there is no difference between the two population means (i.e., d = 0), the null and alternative hypothesis are often stated in the following form.

H o : μ 1 = μ 2

H a : μ 1 ≠ μ 2

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. It should specify the following elements.

• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Use the two-sample t-test to determine whether the difference between means found in the sample is significantly different from the hypothesized difference between means.

Analyze Sample Data

Using sample data, find the standard error, degrees of freedom, test statistic, and the P-value associated with the test statistic.

SE = sqrt[ (s 1 2 /n 1 ) + (s 2 2 /n 2 ) ]

DF = (s 1 2 /n 1 + s 2 2 /n 2 ) 2 / { [ (s 1 2 / n 1 ) 2 / (n 1 - 1) ] + [ (s 2 2 / n 2 ) 2 / (n 2 - 1) ] }

t = [ ( x 1 - x 2 ) - d ] / SE

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the t statistic, having the degrees of freedom computed above. (See sample problems at the end of this lesson for examples of how this is done.)

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

In this section, two sample problems illustrate how to conduct a hypothesis test of a difference between mean scores. The first problem involves a two-tailed test; the second problem, a one-tailed test.

Problem 1: Two-Tailed Test

Within a school district, students were randomly assigned to one of two Math teachers - Mrs. Smith and Mrs. Jones. After the assignment, Mrs. Smith had 30 students, and Mrs. Jones had 25 students.

At the end of the year, each class took the same standardized test. Mrs. Smith's students had an average test score of 78, with a standard deviation of 10; and Mrs. Jones' students had an average test score of 85, with a standard deviation of 15.

Test the hypothesis that Mrs. Smith and Mrs. Jones are equally effective teachers. Use a 0.10 level of significance. (Assume that student performance is approximately normal.)

Solution: The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

State the hypotheses. The first step is to state the null hypothesis and an alternative hypothesis.

Null hypothesis: μ 1 - μ 2 = 0

Alternative hypothesis: μ 1 - μ 2 ≠ 0

• Formulate an analysis plan . For this analysis, the significance level is 0.10. Using sample data, we will conduct a two-sample t-test of the null hypothesis.

SE = sqrt[(s 1 2 /n 1 ) + (s 2 2 /n 2 )]

SE = sqrt[(10 2 /30) + (15 2 /25] = sqrt(3.33 + 9)

SE = sqrt(12.33) = 3.51

DF = (10 2 /30 + 15 2 /25) 2 / { [ (10 2 / 30) 2 / (29) ] + [ (15 2 / 25) 2 / (24) ] }

DF = (3.33 + 9) 2 / { [ (3.33) 2 / (29) ] + [ (9) 2 / (24) ] } = 152.03 / (0.382 + 3.375) = 152.03/3.757 = 40.47

t = [ ( x 1 - x 2 ) - d ] / SE = [ (78 - 85) - 0 ] / 3.51 = -7/3.51 = -1.99

where s 1 is the standard deviation of sample 1, s 2 is the standard deviation of sample 2, n 1 is the size of sample 1, n 2 is the size of sample 2, x 1 is the mean of sample 1, x 2 is the mean of sample 2, d is the hypothesized difference between the population means, and SE is the standard error.

Since we have a two-tailed test , the P-value is the probability that a t statistic having 40 degrees of freedom is more extreme than -1.99; that is, less than -1.99 or greater than 1.99.

We use the t Distribution Calculator to find P(t < -1.99) is about 0.027.

• If you enter 1.99 as the sample mean in the t Distribution Calculator, you will find the that the P(t ≤ 1.99) is about 0.973. Therefore, P(t > 1.99) is 1 minus 0.973 or 0.027. Thus, the P-value = 0.027 + 0.027 = 0.054.
• Interpret results . Since the P-value (0.054) is less than the significance level (0.10), we cannot accept the null hypothesis.

Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the samples were independent, the sample size was much smaller than the population size, and the samples were drawn from a normal population.

Problem 2: One-Tailed Test

The Acme Company has developed a new battery. The engineer in charge claims that the new battery will operate continuously for at least 7 minutes longer than the old battery.

To test the claim, the company selects a simple random sample of 100 new batteries and 100 old batteries. The old batteries run continuously for 190 minutes with a standard deviation of 20 minutes; the new batteries, 200 minutes with a standard deviation of 40 minutes.

Test the engineer's claim that the new batteries run at least 7 minutes longer than the old. Use a 0.05 level of significance. (Assume that there are no outliers in either sample.)

Null hypothesis: μ 1 - μ 2 <= 7

Alternative hypothesis: μ 1 - μ 2 > 7

where μ 1 is battery life for the new battery, and μ 2 is battery life for the old battery.

• Formulate an analysis plan . For this analysis, the significance level is 0.05. Using sample data, we will conduct a two-sample t-test of the null hypothesis.

SE = sqrt[(40 2 /100) + (20 2 /100]

SE = sqrt(16 + 4) = 4.472

DF = (40 2 /100 + 20 2 /100) 2 / { [ (40 2 / 100) 2 / (99) ] + [ (20 2 / 100) 2 / (99) ] }

DF = (20) 2 / { [ (16) 2 / (99) ] + [ (2) 2 / (99) ] } = 400 / (2.586 + 0.162) = 145.56

t = [ ( x 1 - x 2 ) - d ] / SE = [(200 - 190) - 7] / 4.472 = 3/4.472 = 0.67

where s 1 is the standard deviation of sample 1, s 2 is the standard deviation of sample 2, n 1 is the size of sample 1, n 2 is the size of sample 2, x 1 is the mean of sample 1, x 2 is the mean of sample 2, d is the hypothesized difference between population means, and SE is the standard error.

Here is the logic of the analysis: Given the alternative hypothesis (μ 1 - μ 2 > 7), we want to know whether the observed difference in sample means is big enough (i.e., sufficiently greater than 7) to cause us to reject the null hypothesis.

Interpret results . Suppose we replicated this study many times with different samples. If the true difference in population means were actually 7, we would expect the observed difference in sample means to be 10 or less in 75% of our samples. And we would expect to find an observed difference to be more than 10 in 25% of our samples Therefore, the P-value in this analysis is 0.25.

Statistics Tutorial

Descriptive statistics, inferential statistics, stat reference, statistics - hypothesis testing a mean.

A population mean is an average of value a population.

Hypothesis tests are used to check a claim about the size of that population mean.

Hypothesis Testing a Mean

The following steps are used for a hypothesis test:

• Check the conditions
• Define the claims
• Decide the significance level
• Calculate the test statistic

For example:

• Population : Nobel Prize winners
• Category : Age when they received the prize.

And we want to check the claim:

"The average age of Nobel Prize winners when they received the prize is more than 55"

By taking a sample of 30 randomly selected Nobel Prize winners we could find that:

The mean age in the sample (\(\bar{x}\)) is 62.1

The standard deviation of age in the sample (\(s\)) is 13.46

From this sample data we check the claim with the steps below.

1. Checking the Conditions

The conditions for calculating a confidence interval for a proportion are:

• The sample is randomly selected
• The population data is normally distributed
• Sample size is large enough

A moderately large sample size, like 30, is typically large enough.

In the example, the sample size was 30 and it was randomly selected, so the conditions are fulfilled.

Note: Checking if the data is normally distributed can be done with specialized statistical tests.

2. Defining the Claims

We need to define a null hypothesis (\(H_{0}\)) and an alternative hypothesis (\(H_{1}\)) based on the claim we are checking.

The claim was:

In this case, the parameter is the mean age of Nobel Prize winners when they received the prize (\(\mu\)).

The null and alternative hypothesis are then:

Null hypothesis : The average age was 55.

Alternative hypothesis : The average age was more than 55.

Which can be expressed with symbols as:

\(H_{0}\): \(\mu = 55 \)

\(H_{1}\): \(\mu > 55 \)

This is a ' right tailed' test, because the alternative hypothesis claims that the proportion is more than in the null hypothesis.

If the data supports the alternative hypothesis, we reject the null hypothesis and accept the alternative hypothesis.

Advertisement

3. Deciding the Significance Level

The significance level (\(\alpha\)) is the uncertainty we accept when rejecting the null hypothesis in a hypothesis test.

The significance level is a percentage probability of accidentally making the wrong conclusion.

Typical significance levels are:

• \(\alpha = 0.1\) (10%)
• \(\alpha = 0.05\) (5%)
• \(\alpha = 0.01\) (1%)

A lower significance level means that the evidence in the data needs to be stronger to reject the null hypothesis.

There is no "correct" significance level - it only states the uncertainty of the conclusion.

Note: A 5% significance level means that when we reject a null hypothesis:

We expect to reject a true null hypothesis 5 out of 100 times.

4. Calculating the Test Statistic

The test statistic is used to decide the outcome of the hypothesis test.

The test statistic is a standardized value calculated from the sample.

The formula for the test statistic (TS) of a population mean is:

\(\displaystyle \frac{\bar{x} - \mu}{s} \cdot \sqrt{n} \)

\(\bar{x}-\mu\) is the difference between the sample mean (\(\bar{x}\)) and the claimed population mean (\(\mu\)).

\(s\) is the sample standard deviation .

\(n\) is the sample size.

In our example:

The claimed (\(H_{0}\)) population mean (\(\mu\)) was \( 55 \)

The sample mean (\(\bar{x}\)) was \(62.1\)

The sample standard deviation (\(s\)) was \(13.46\)

The sample size (\(n\)) was \(30\)

So the test statistic (TS) is then:

\(\displaystyle \frac{62.1-55}{13.46} \cdot \sqrt{30} = \frac{7.1}{13.46} \cdot \sqrt{30} \approx 0.528 \cdot 5.477 = \underline{2.889}\)

You can also calculate the test statistic using programming language functions:

With Python use the scipy and math libraries to calculate the test statistic.

With R use built-in math and statistics functions to calculate the test statistic.

5. Concluding

There are two main approaches for making the conclusion of a hypothesis test:

• The critical value approach compares the test statistic with the critical value of the significance level.
• The P-value approach compares the P-value of the test statistic and with the significance level.

Note: The two approaches are only different in how they present the conclusion.

The Critical Value Approach

For the critical value approach we need to find the critical value (CV) of the significance level (\(\alpha\)).

For a population mean test, the critical value (CV) is a T-value from a student's t-distribution .

This critical T-value (CV) defines the rejection region for the test.

The rejection region is an area of probability in the tails of the standard normal distribution.

Because the claim is that the population mean is more than 55, the rejection region is in the right tail:

The student's t-distribution is adjusted for the uncertainty from smaller samples.

This adjustment is called degrees of freedom (df), which is the sample size \((n) - 1\)

In this case the degrees of freedom (df) is: \(30 - 1 = \underline{29} \)

Choosing a significance level (\(\alpha\)) of 0.01, or 1%, we can find the critical T-value from a T-table , or with a programming language function:

With Python use the Scipy Stats library t.ppf() function find the T-Value for an \(\alpha\) = 0.01 at 29 degrees of freedom (df).

With R use the built-in qt() function to find the t-value for an \(\alpha\) = 0.01 at 29 degrees of freedom (df).

Using either method we can find that the critical T-Value is \(\approx \underline{2.462}\)

For a right tailed test we need to check if the test statistic (TS) is bigger than the critical value (CV).

If the test statistic is bigger than the critical value, the test statistic is in the rejection region .

When the test statistic is in the rejection region, we reject the null hypothesis (\(H_{0}\)).

Here, the test statistic (TS) was \(\approx \underline{2.889}\) and the critical value was \(\approx \underline{2.462}\)

Here is an illustration of this test in a graph:

Since the test statistic was bigger than the critical value we reject the null hypothesis.

This means that the sample data supports the alternative hypothesis.

And we can summarize the conclusion stating:

The sample data supports the claim that "The average age of Nobel Prize winners when they received the prize is more than 55" at a 1% significance level .

The P-Value Approach

For the P-value approach we need to find the P-value of the test statistic (TS).

If the P-value is smaller than the significance level (\(\alpha\)), we reject the null hypothesis (\(H_{0}\)).

The test statistic was found to be \( \approx \underline{2.889} \)

For a population proportion test, the test statistic is a T-Value from a student's t-distribution .

Because this is a right tailed test, we need to find the P-value of a t-value bigger than 2.889.

The student's t-distribution is adjusted according to degrees of freedom (df), which is the sample size \((30) - 1 = \underline{29}\)

We can find the P-value using a T-table , or with a programming language function:

With Python use the Scipy Stats library t.cdf() function find the P-value of a T-value bigger than 2.889 at 29 degrees of freedom (df):

With R use the built-in pt() function find the P-value of a T-Value bigger than 2.889 at 29 degrees of freedom (df):

Using either method we can find that the P-value is \(\approx \underline{0.0036}\)

This tells us that the significance level (\(\alpha\)) would need to be bigger than 0.0036, or 0.36%, to reject the null hypothesis.

This P-value is smaller than any of the common significance levels (10%, 5%, 1%).

So the null hypothesis is rejected at all of these significance levels.

The sample data supports the claim that "The average age of Nobel Prize winners when they received the prize is more than 55" at a 10%, 5%, or 1% significance level .

Note: An outcome of an hypothesis test that rejects the null hypothesis with a p-value of 0.36% means:

For this p-value, we only expect to reject a true null hypothesis 36 out of 10000 times.

Calculating a P-Value for a Hypothesis Test with Programming

Many programming languages can calculate the P-value to decide outcome of a hypothesis test.

Using software and programming to calculate statistics is more common for bigger sets of data, as calculating manually becomes difficult.

The P-value calculated here will tell us the lowest possible significance level where the null-hypothesis can be rejected.

With Python use the scipy and math libraries to calculate the P-value for a right tailed hypothesis test for a mean.

Here, the sample size is 30, the sample mean is 62.1, the sample standard deviation is 13.46, and the test is for a mean bigger than 55.

With R use built-in math and statistics functions find the P-value for a right tailed hypothesis test for a mean.

Left-Tailed and Two-Tailed Tests

This was an example of a right tailed test, where the alternative hypothesis claimed that parameter is bigger than the null hypothesis claim.

You can check out an equivalent step-by-step guide for other types here:

• Left-Tailed Test
• Two-Tailed Test

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

Top Tutorials

Top references, top examples, get certified.

Help | Advanced Search

Mathematics > Statistics Theory

Title: general linear hypothesis testing of high-dimensional mean vectors with unequal covariance matrices based on random integration.

Abstract: This paper is devoted to the study of the general linear hypothesis testing (GLHT) problem of multi-sample high-dimensional mean vectors. For the GLHT problem, we introduce a test statistic based on $L^2$-norm and random integration method, and deduce the asymptotic distribution of the statistic under given conditions. Finally, the potential advantages of our test statistics are verified by numerical simulation studies and examples.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .