ANOVA Test: Definition, Types, Examples, SPSS
Statistics Definitions > ANOVA Contents :

The ANOVA Test
- How to Run a One Way ANOVA in SPSS
Two Way ANOVA
What is manova, what is factorial anova, how to run an anova, anova vs. t test.
- Repeated Measures ANOVA in SPSS: Steps
Related Articles
An ANOVA test is a way to find out if survey or experiment results are significant . In other words, they help you to figure out if you need to reject the null hypothesis or accept the alternate hypothesis .
Basically, you’re testing groups to see if there’s a difference between them. Examples of when you might want to test different groups:
- A group of psychiatric patients are trying three different therapies: counseling, medication and biofeedback. You want to see if one therapy is better than the others.
- A manufacturer has two different processes to make light bulbs. They want to know if one process is better than the other.
- Students from different colleges take the same exam. You want to see if one college outperforms the other.
What Does “One-Way” or “Two-Way Mean?
One-way or two-way refers to the number of independent variables (IVs) in your Analysis of Variance test.
- One-way has one independent variable (with 2 levels ). For example: brand of cereal ,
- Two-way has two independent variables (it can have multiple levels). For example: brand of cereal, calories .
What are “Groups” or “Levels”?
Groups or levels are different groups within the same independent variable . In the above example, your levels for “brand of cereal” might be Lucky Charms, Raisin Bran, Cornflakes — a total of three levels. Your levels for “Calories” might be: sweetened, unsweetened — a total of two levels.
Let’s say you are studying if an alcoholic support group and individual counseling combined is the most effective treatment for lowering alcohol consumption. You might split the study participants into three groups or levels:
- Medication only,
- Medication and counseling,
- Counseling only.
Your dependent variable would be the number of alcoholic beverages consumed per day.
If your groups or levels have a hierarchical structure (each level has unique subgroups), then use a nested ANOVA for the analysis.
What Does “Replication” Mean?
It’s whether you are replicating (i.e. duplicating) your test(s) with multiple groups. With a two way ANOVA with replication , you have two groups and individuals within that group are doing more than one thing (i.e. two groups of students from two colleges taking two tests). If you only have one group taking two tests, you would use without replication.
Types of Tests.
There are two main types: one-way and two-way. Two-way tests can be with or without replication.
- One-way ANOVA between groups: used when you want to test two groups to see if there’s a difference between them.
- Two way ANOVA without replication: used when you have one group and you’re double-testing that same group. For example, you’re testing one set of individuals before and after they take a medication to see if it works or not.
- Two way ANOVA with replication: Two groups , and the members of those groups are doing more than one thing . For example, two groups of patients from different hospitals trying two different therapies.
Back to Top
One Way ANOVA
A one way ANOVA is used to compare two means from two independent (unrelated) groups using the F-distribution . The null hypothesis for the test is that the two means are equal. Therefore, a significant result means that the two means are unequal.
Examples of when to use a one way ANOVA
Situation 1: You have a group of individuals randomly split into smaller groups and completing different tasks. For example, you might be studying the effects of tea on weight loss and form three groups: green tea, black tea, and no tea. Situation 2: Similar to situation 1, but in this case the individuals are split into groups based on an attribute they possess. For example, you might be studying leg strength of people according to weight. You could split participants into weight categories (obese, overweight and normal) and measure their leg strength on a weight machine.
Limitations of the One Way ANOVA
A one way ANOVA will tell you that at least two groups were different from each other. But it won’t tell you which groups were different. If your test returns a significant f-statistic, you may need to run an ad hoc test (like the Least Significant Difference test) to tell you exactly which groups had a difference in means . Back to Top
How to run a One Way ANOVA in SPSS
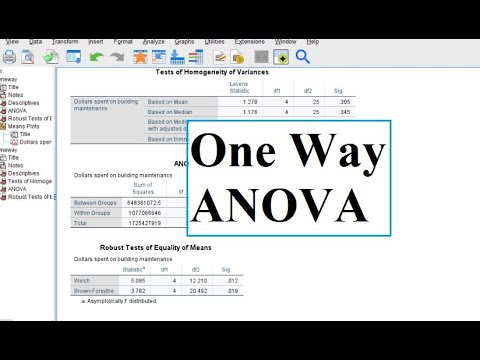
A Two Way ANOVA is an extension of the One Way ANOVA. With a One Way, you have one independent variable affecting a dependent variable . With a Two Way ANOVA, there are two independents. Use a two way ANOVA when you have one measurement variable (i.e. a quantitative variable ) and two nominal variables . In other words, if your experiment has a quantitative outcome and you have two categorical explanatory variables , a two way ANOVA is appropriate.
For example, you might want to find out if there is an interaction between income and gender for anxiety level at job interviews. The anxiety level is the outcome, or the variable that can be measured. Gender and Income are the two categorical variables . These categorical variables are also the independent variables, which are called factors in a Two Way ANOVA.
The factors can be split into levels . In the above example, income level could be split into three levels: low, middle and high income. Gender could be split into three levels: male, female, and transgender. Treatment groups are all possible combinations of the factors. In this example there would be 3 x 3 = 9 treatment groups.
Main Effect and Interaction Effect
The results from a Two Way ANOVA will calculate a main effect and an interaction effect . The main effect is similar to a One Way ANOVA: each factor’s effect is considered separately. With the interaction effect, all factors are considered at the same time. Interaction effects between factors are easier to test if there is more than one observation in each cell. For the above example, multiple stress scores could be entered into cells. If you do enter multiple observations into cells, the number in each cell must be equal.
Two null hypotheses are tested if you are placing one observation in each cell. For this example, those hypotheses would be: H 01 : All the income groups have equal mean stress. H 02 : All the gender groups have equal mean stress.
For multiple observations in cells, you would also be testing a third hypothesis: H 03 : The factors are independent or the interaction effect does not exist.
An F-statistic is computed for each hypothesis you are testing.
Assumptions for Two Way ANOVA
- The population must be close to a normal distribution .
- Samples must be independent.
- Population variances must be equal (i.e. homoscedastic ).
- Groups must have equal sample sizes .
MANOVA is just an ANOVA with several dependent variables. It’s similar to many other tests and experiments in that it’s purpose is to find out if the response variable (i.e. your dependent variable) is changed by manipulating the independent variable. The test helps to answer many research questions, including:
- Do changes to the independent variables have statistically significant effects on dependent variables?
- What are the interactions among dependent variables?
- What are the interactions among independent variables?
MANOVA Example
Suppose you wanted to find out if a difference in textbooks affected students’ scores in math and science. Improvements in math and science means that there are two dependent variables, so a MANOVA is appropriate.
An ANOVA will give you a single ( univariate ) f-value while a MANOVA will give you a multivariate F value. MANOVA tests the multiple dependent variables by creating new, artificial, dependent variables that maximize group differences. These new dependent variables are linear combinations of the measured dependent variables.
Interpreting the MANOVA results
If the multivariate F value indicates the test is statistically significant , this means that something is significant. In the above example, you would not know if math scores have improved, science scores have improved (or both). Once you have a significant result, you would then have to look at each individual component (the univariate F tests) to see which dependent variable(s) contributed to the statistically significant result.
Advantages and Disadvantages of MANOVA vs. ANOVA
- MANOVA enables you to test multiple dependent variables.
- MANOVA can protect against Type I errors.
Disadvantages
- MANOVA is many times more complicated than ANOVA, making it a challenge to see which independent variables are affecting dependent variables.
- One degree of freedom is lost with the addition of each new variable .
- The dependent variables should be uncorrelated as much as possible. If they are correlated, the loss in degrees of freedom means that there isn’t much advantages in including more than one dependent variable on the test.
Reference : SFSU. Retrieved April 18, 2022 from: http://online.sfsu.edu/efc/classes/biol710/manova/MANOVAnewest.pdf
A factorial ANOVA is an Analysis of Variance test with more than one independent variable , or “ factor “. It can also refer to more than one Level of Independent Variable . For example, an experiment with a treatment group and a control group has one factor (the treatment) but two levels (the treatment and the control). The terms “two-way” and “three-way” refer to the number of factors or the number of levels in your test. Four-way ANOVA and above are rarely used because the results of the test are complex and difficult to interpret.
- A two-way ANOVA has two factors ( independent variables ) and one dependent variable . For example, time spent studying and prior knowledge are factors that affect how well you do on a test.
- A three-way ANOVA has three factors (independent variables) and one dependent variable. For example, time spent studying, prior knowledge, and hours of sleep are factors that affect how well you do on a test
Factorial ANOVA is an efficient way of conducting a test. Instead of performing a series of experiments where you test one independent variable against one dependent variable, you can test all independent variables at the same time.
Variability
In a one-way ANOVA, variability is due to the differences between groups and the differences within groups. In factorial ANOVA, each level and factor are paired up with each other (“crossed”). This helps you to see what interactions are going on between the levels and factors. If there is an interaction then the differences in one factor depend on the differences in another.
Let’s say you were running a two-way ANOVA to test male/female performance on a final exam. The subjects had either had 4, 6, or 8 hours of sleep.
- IV1: SEX (Male/Female)
- IV2: SLEEP (4/6/8)
- DV: Final Exam Score
A two-way factorial ANOVA would help you answer the following questions:
- Is sex a main effect? In other words, do men and women differ significantly on their exam performance?
- Is sleep a main effect? In other words, do people who have had 4,6, or 8 hours of sleep differ significantly in their performance?
- Is there a significant interaction between factors? In other words, how do hours of sleep and sex interact with regards to exam performance?
- Can any differences in sex and exam performance be found in the different levels of sleep?
Assumptions of Factorial ANOVA
- Normality: the dependent variable is normally distributed.
- Independence: Observations and groups are independent from each other.
- Equality of Variance: the population variances are equal across factors/levels.
These tests are very time-consuming by hand. In nearly every case you’ll want to use software. For example, several options are available in Excel :
- Two way ANOVA in Excel with replication and without replication.
- One way ANOVA in Excel 2013 .
ANOVA tests in statistics packages are run on parametric data. If you have rank or ordered data, you’ll want to run a non-parametric ANOVA (usually found under a different heading in the software, like “ nonparametric tests “).
It is unlikely you’ll want to do this test by hand, but if you must, these are the steps you’ll want to take:
- Find the mean for each of the groups.
- Find the overall mean (the mean of the groups combined).
- Find the Within Group Variation ; the total deviation of each member’s score from the Group Mean.
- Find the Between Group Variation : the deviation of each Group Mean from the Overall Mean.
- Find the F statistic: the ratio of Between Group Variation to Within Group Variation.
A Student’s t-test will tell you if there is a significant variation between groups. A t-test compares means, while the ANOVA compares variances between populations. You could technically perform a series of t-tests on your data. However, as the groups grow in number, you may end up with a lot of pair comparisons that you need to run. ANOVA will give you a single number (the f-statistic ) and one p-value to help you support or reject the null hypothesis . Back to Top
Repeated Measures (Within Subjects) ANOVA
A repeated measures ANOVA is almost the same as one-way ANOVA, with one main difference: you test related groups, not independent ones.
It’s called Repeated Measures because the same group of participants is being measured over and over again. For example, you could be studying the cholesterol levels of the same group of patients at 1, 3, and 6 months after changing their diet. For this example, the independent variable is “time” and the dependent variable is “cholesterol.” The independent variable is usually called the within-subjects factor .
Repeated measures ANOVA is similar to a simple multivariate design. In both tests, the same participants are measured over and over. However, with repeated measures the same characteristic is measured with a different condition. For example, blood pressure is measured over the condition “time”. For simple multivariate design it is the characteristic that changes. For example, you could measure blood pressure, heart rate and respiration rate over time.
Reasons to use Repeated Measures ANOVA
- When you collect data from the same participants over a period of time, individual differences (a source of between group differences) are reduced or eliminated.
- Testing is more powerful because the sample size isn’t divided between groups.
- The test can be economical, as you’re using the same participants.
Assumptions for Repeated Measures ANOVA
The results from your repeated measures ANOVA will be valid only if the following assumptions haven’t been violated:
- There must be one independent variable and one dependent variable.
- The dependent variable must be a continuous variable , on an interval scale or a ratio scale .
- The independent variable must be categorical , either on the nominal scale or ordinal scale.
- Ideally, levels of dependence between pairs of groups is equal (“sphericity”). Corrections are possible if this assumption is violated.
One Way Repeated Measures ANOVA in SPSS: Steps
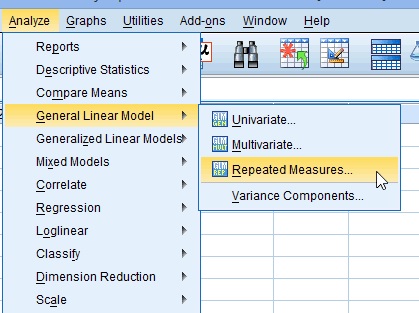
Step 2: Replace the “factor1” name with something that represents your independent variable. For example, you could put “age” or “time.”
Step 3: Enter the “Number of Levels.” This is how many times the dependent variable has been measured. For example, if you took measurements every week for a total of 4 weeks, this number would be 4.
Step 4: Click the “Add” button and then give your dependent variable a name.
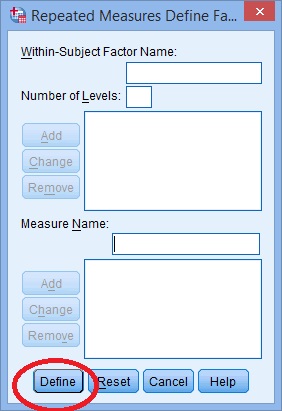
Step 7: Click “Plots” and use the arrow keys to transfer the factor from the left box onto the Horizontal Axis box.
Step 9: Click “Options”, then transfer your factors from the left box to the Display Means for box on the right.
Step 10: Click the following check boxes:
- Compare main effects.
- Descriptive Statistics.
- Estimates of Effect Size .
Step 11: Select “Bonferroni” from the drop down menu under Confidence Interval Adjustment . Step 12: Click “Continue” and then click “OK” to run the test. Back to Top
In statistics, sphericity (ε) refers to Mauchly’s sphericity test , which was developed in 1940 by John W. Mauchly , who co-developed the first general-purpose electronic computer.
Sphericity is used as an assumption in repeated measures ANOVA. The assumption states that the variances of the differences between all possible group pairs are equal. If your data violates this assumption, it can result in an increase in a Type I error (the incorrect rejection of the null hypothesis) .
It’s very common for repeated measures ANOVA to result in a violation of the assumption. If the assumption has been violated, corrections have been developed that can avoid increases in the type I error rate. The correction is applied to the degrees of freedom in the F-distribution .
Mauchly’s Sphericity Test
Mauchly’s test for sphericity can be run in the majority of statistical software, where it tends to be the default test for sphericity. Mauchly’s test is ideal for mid-size samples. It may fail to detect sphericity in small samples and it may over-detect in large samples. If the test returns a small p-value (p ≤.05), this is an indication that your data has violated the assumption. The following picture of SPSS output for ANOVA shows that the significance “sig” attached to Mauchly’s is .274. This means that the assumption has not been violated for this set of data.
You would report the above result as “Mauchly’s Test indicated that the assumption of sphericity had not been violated, χ 2 (2) = 2.588, p = .274.”
If your test returned a small p-value , you should apply a correction, usually either the:
- Greehouse-Geisser correction.
- Huynh-Feldt correction .
When ε ≤ 0.75 (or you don’t know what the value for the statistic is), use the Greenhouse-Geisser correction. When ε > .75, use the Huynh-Feldt correction .
Grand mean ANOVA vs Regression
Blokdyk, B. (2018). Ad Hoc Testing . 5STARCooks Miller, R. G. Beyond ANOVA: Basics of Applied Statistics . Boca Raton, FL: Chapman & Hall, 1997 Image: UVM. Retrieved December 4, 2020 from: https://www.uvm.edu/~dhowell/gradstat/psych341/lectures/RepeatedMeasures/repeated1.html
- Privacy Policy

Home » ANOVA (Analysis of variance) – Formulas, Types, and Examples
ANOVA (Analysis of variance) – Formulas, Types, and Examples
Table of Contents

Analysis of Variance (ANOVA)
Analysis of Variance (ANOVA) is a statistical method used to test differences between two or more means. It is similar to the t-test, but the t-test is generally used for comparing two means, while ANOVA is used when you have more than two means to compare.
ANOVA is based on comparing the variance (or variation) between the data samples to the variation within each particular sample. If the between-group variance is high and the within-group variance is low, this provides evidence that the means of the groups are significantly different.
ANOVA Terminology
When discussing ANOVA, there are several key terms to understand:
- Factor : This is another term for the independent variable in your analysis. In a one-way ANOVA, there is one factor, while in a two-way ANOVA, there are two factors.
- Levels : These are the different groups or categories within a factor. For example, if the factor is ‘diet’ the levels might be ‘low fat’, ‘medium fat’, and ‘high fat’.
- Response Variable : This is the dependent variable or the outcome that you are measuring.
- Within-group Variance : This is the variance or spread of scores within each level of your factor.
- Between-group Variance : This is the variance or spread of scores between the different levels of your factor.
- Grand Mean : This is the overall mean when you consider all the data together, regardless of the factor level.
- Treatment Sums of Squares (SS) : This represents the between-group variability. It is the sum of the squared differences between the group means and the grand mean.
- Error Sums of Squares (SS) : This represents the within-group variability. It’s the sum of the squared differences between each observation and its group mean.
- Total Sums of Squares (SS) : This is the sum of the Treatment SS and the Error SS. It represents the total variability in the data.
- Degrees of Freedom (df) : The degrees of freedom are the number of values that have the freedom to vary when computing a statistic. For example, if you have ‘n’ observations in one group, then the degrees of freedom for that group is ‘n-1’.
- Mean Square (MS) : Mean Square is the average squared deviation and is calculated by dividing the sum of squares by the corresponding degrees of freedom.
- F-Ratio : This is the test statistic for ANOVAs, and it’s the ratio of the between-group variance to the within-group variance. If the between-group variance is significantly larger than the within-group variance, the F-ratio will be large and likely significant.
- Null Hypothesis (H0) : This is the hypothesis that there is no difference between the group means.
- Alternative Hypothesis (H1) : This is the hypothesis that there is a difference between at least two of the group means.
- p-value : This is the probability of obtaining a test statistic as extreme as the one that was actually observed, assuming that the null hypothesis is true. If the p-value is less than the significance level (usually 0.05), then the null hypothesis is rejected in favor of the alternative hypothesis.
- Post-hoc tests : These are follow-up tests conducted after an ANOVA when the null hypothesis is rejected, to determine which specific groups’ means (levels) are different from each other. Examples include Tukey’s HSD, Scheffe, Bonferroni, among others.
Types of ANOVA
Types of ANOVA are as follows:
One-way (or one-factor) ANOVA
This is the simplest type of ANOVA, which involves one independent variable . For example, comparing the effect of different types of diet (vegetarian, pescatarian, omnivore) on cholesterol level.
Two-way (or two-factor) ANOVA
This involves two independent variables. This allows for testing the effect of each independent variable on the dependent variable , as well as testing if there’s an interaction effect between the independent variables on the dependent variable.
Repeated Measures ANOVA
This is used when the same subjects are measured multiple times under different conditions, or at different points in time. This type of ANOVA is often used in longitudinal studies.
Mixed Design ANOVA
This combines features of both between-subjects (independent groups) and within-subjects (repeated measures) designs. In this model, one factor is a between-subjects variable and the other is a within-subjects variable.
Multivariate Analysis of Variance (MANOVA)
This is used when there are two or more dependent variables. It tests whether changes in the independent variable(s) correspond to changes in the dependent variables.
Analysis of Covariance (ANCOVA)
This combines ANOVA and regression. ANCOVA tests whether certain factors have an effect on the outcome variable after removing the variance for which quantitative covariates (interval variables) account. This allows the comparison of one variable outcome between groups, while statistically controlling for the effect of other continuous variables that are not of primary interest.
Nested ANOVA
This model is used when the groups can be clustered into categories. For example, if you were comparing students’ performance from different classrooms and different schools, “classroom” could be nested within “school.”
ANOVA Formulas
ANOVA Formulas are as follows:
Sum of Squares Total (SST)
This represents the total variability in the data. It is the sum of the squared differences between each observation and the overall mean.
- yi represents each individual data point
- y_mean represents the grand mean (mean of all observations)
Sum of Squares Within (SSW)
This represents the variability within each group or factor level. It is the sum of the squared differences between each observation and its group mean.
- yij represents each individual data point within a group
- y_meani represents the mean of the ith group
Sum of Squares Between (SSB)
This represents the variability between the groups. It is the sum of the squared differences between the group means and the grand mean, multiplied by the number of observations in each group.
- ni represents the number of observations in each group
- y_mean represents the grand mean
Degrees of Freedom
The degrees of freedom are the number of values that have the freedom to vary when calculating a statistic.
For within groups (dfW):
For between groups (dfB):
For total (dfT):
- N represents the total number of observations
- k represents the number of groups
Mean Squares
Mean squares are the sum of squares divided by the respective degrees of freedom.
Mean Squares Between (MSB):
Mean Squares Within (MSW):
F-Statistic
The F-statistic is used to test whether the variability between the groups is significantly greater than the variability within the groups.
If the F-statistic is significantly higher than what would be expected by chance, we reject the null hypothesis that all group means are equal.
Examples of ANOVA
Examples 1:
Suppose a psychologist wants to test the effect of three different types of exercise (yoga, aerobic exercise, and weight training) on stress reduction. The dependent variable is the stress level, which can be measured using a stress rating scale.
Here are hypothetical stress ratings for a group of participants after they followed each of the exercise regimes for a period:
- Yoga: [3, 2, 2, 1, 2, 2, 3, 2, 1, 2]
- Aerobic Exercise: [2, 3, 3, 2, 3, 2, 3, 3, 2, 2]
- Weight Training: [4, 4, 5, 5, 4, 5, 4, 5, 4, 5]
The psychologist wants to determine if there is a statistically significant difference in stress levels between these different types of exercise.
To conduct the ANOVA:
1. State the hypotheses:
- Null Hypothesis (H0): There is no difference in mean stress levels between the three types of exercise.
- Alternative Hypothesis (H1): There is a difference in mean stress levels between at least two of the types of exercise.
2. Calculate the ANOVA statistics:
- Compute the Sum of Squares Between (SSB), Sum of Squares Within (SSW), and Sum of Squares Total (SST).
- Calculate the Degrees of Freedom (dfB, dfW, dfT).
- Calculate the Mean Squares Between (MSB) and Mean Squares Within (MSW).
- Compute the F-statistic (F = MSB / MSW).
3. Check the p-value associated with the calculated F-statistic.
- If the p-value is less than the chosen significance level (often 0.05), then we reject the null hypothesis in favor of the alternative hypothesis. This suggests there is a statistically significant difference in mean stress levels between the three exercise types.
4. Post-hoc tests
- If we reject the null hypothesis, we conduct a post-hoc test to determine which specific groups’ means (exercise types) are different from each other.
Examples 2:
Suppose an agricultural scientist wants to compare the yield of three varieties of wheat. The scientist randomly selects four fields for each variety and plants them. After harvest, the yield from each field is measured in bushels. Here are the hypothetical yields:
The scientist wants to know if the differences in yields are due to the different varieties or just random variation.
Here’s how to apply the one-way ANOVA to this situation:
- Null Hypothesis (H0): The means of the three populations are equal.
- Alternative Hypothesis (H1): At least one population mean is different.
- Calculate the Degrees of Freedom (dfB for between groups, dfW for within groups, dfT for total).
- If the p-value is less than the chosen significance level (often 0.05), then we reject the null hypothesis in favor of the alternative hypothesis. This would suggest there is a statistically significant difference in mean yields among the three varieties.
- If we reject the null hypothesis, we conduct a post-hoc test to determine which specific groups’ means (wheat varieties) are different from each other.
How to Conduct ANOVA
Conducting an Analysis of Variance (ANOVA) involves several steps. Here’s a general guideline on how to perform it:
- Null Hypothesis (H0): The means of all groups are equal.
- Alternative Hypothesis (H1): At least one group mean is different from the others.
- The significance level (often denoted as α) is usually set at 0.05. This implies that you are willing to accept a 5% chance that you are wrong in rejecting the null hypothesis.
- Data should be collected for each group under study. Make sure that the data meet the assumptions of an ANOVA: normality, independence, and homogeneity of variances.
- Calculate the Degrees of Freedom (df) for each sum of squares (dfB, dfW, dfT).
- Compute the Mean Squares Between (MSB) and Mean Squares Within (MSW) by dividing the sum of squares by the corresponding degrees of freedom.
- Compute the F-statistic as the ratio of MSB to MSW.
- Determine the critical F-value from the F-distribution table using dfB and dfW.
- If the calculated F-statistic is greater than the critical F-value, reject the null hypothesis.
- If the p-value associated with the calculated F-statistic is smaller than the significance level (0.05 typically), you reject the null hypothesis.
- If you rejected the null hypothesis, you can conduct post-hoc tests (like Tukey’s HSD) to determine which specific groups’ means (if you have more than two groups) are different from each other.
- Regardless of the result, report your findings in a clear, understandable manner. This typically includes reporting the test statistic, p-value, and whether the null hypothesis was rejected.
When to use ANOVA
ANOVA (Analysis of Variance) is used when you have three or more groups and you want to compare their means to see if they are significantly different from each other. It is a statistical method that is used in a variety of research scenarios. Here are some examples of when you might use ANOVA:
- Comparing Groups : If you want to compare the performance of more than two groups, for example, testing the effectiveness of different teaching methods on student performance.
- Evaluating Interactions : In a two-way or factorial ANOVA, you can test for an interaction effect. This means you are not only interested in the effect of each individual factor, but also whether the effect of one factor depends on the level of another factor.
- Repeated Measures : If you have measured the same subjects under different conditions or at different time points, you can use repeated measures ANOVA to compare the means of these repeated measures while accounting for the correlation between measures from the same subject.
- Experimental Designs : ANOVA is often used in experimental research designs when subjects are randomly assigned to different conditions and the goal is to compare the means of the conditions.
Here are the assumptions that must be met to use ANOVA:
- Normality : The data should be approximately normally distributed.
- Homogeneity of Variances : The variances of the groups you are comparing should be roughly equal. This assumption can be tested using Levene’s test or Bartlett’s test.
- Independence : The observations should be independent of each other. This assumption is met if the data is collected appropriately with no related groups (e.g., twins, matched pairs, repeated measures).
Applications of ANOVA
The Analysis of Variance (ANOVA) is a powerful statistical technique that is used widely across various fields and industries. Here are some of its key applications:
Agriculture
ANOVA is commonly used in agricultural research to compare the effectiveness of different types of fertilizers, crop varieties, or farming methods. For example, an agricultural researcher could use ANOVA to determine if there are significant differences in the yields of several varieties of wheat under the same conditions.
Manufacturing and Quality Control
ANOVA is used to determine if different manufacturing processes or machines produce different levels of product quality. For instance, an engineer might use it to test whether there are differences in the strength of a product based on the machine that produced it.
Marketing Research
Marketers often use ANOVA to test the effectiveness of different advertising strategies. For example, a marketer could use ANOVA to determine whether different marketing messages have a significant impact on consumer purchase intentions.
Healthcare and Medicine
In medical research, ANOVA can be used to compare the effectiveness of different treatments or drugs. For example, a medical researcher could use ANOVA to test whether there are significant differences in recovery times for patients who receive different types of therapy.
ANOVA is used in educational research to compare the effectiveness of different teaching methods or educational interventions. For example, an educator could use it to test whether students perform significantly differently when taught with different teaching methods.
Psychology and Social Sciences
Psychologists and social scientists use ANOVA to compare group means on various psychological and social variables. For example, a psychologist could use it to determine if there are significant differences in stress levels among individuals in different occupations.
Biology and Environmental Sciences
Biologists and environmental scientists use ANOVA to compare different biological and environmental conditions. For example, an environmental scientist could use it to determine if there are significant differences in the levels of a pollutant in different bodies of water.
Advantages of ANOVA
Here are some advantages of using ANOVA:
Comparing Multiple Groups: One of the key advantages of ANOVA is the ability to compare the means of three or more groups. This makes it more powerful and flexible than the t-test, which is limited to comparing only two groups.
Control of Type I Error: When comparing multiple groups, the chances of making a Type I error (false positive) increases. One of the strengths of ANOVA is that it controls the Type I error rate across all comparisons. This is in contrast to performing multiple pairwise t-tests which can inflate the Type I error rate.
Testing Interactions: In factorial ANOVA, you can test not only the main effect of each factor, but also the interaction effect between factors. This can provide valuable insights into how different factors or variables interact with each other.
Handling Continuous and Categorical Variables: ANOVA can handle both continuous and categorical variables . The dependent variable is continuous and the independent variables are categorical.
Robustness: ANOVA is considered robust to violations of normality assumption when group sizes are equal. This means that even if your data do not perfectly meet the normality assumption, you might still get valid results.
Provides Detailed Analysis: ANOVA provides a detailed breakdown of variances and interactions between variables which can be useful in understanding the underlying factors affecting the outcome.
Capability to Handle Complex Experimental Designs: Advanced types of ANOVA (like repeated measures ANOVA, MANOVA, etc.) can handle more complex experimental designs, including those where measurements are taken on the same subjects over time, or when you want to analyze multiple dependent variables at once.
Disadvantages of ANOVA
Some limitations or disadvantages that are important to consider:
Assumptions: ANOVA relies on several assumptions including normality (the data follows a normal distribution), independence (the observations are independent of each other), and homogeneity of variances (the variances of the groups are roughly equal). If these assumptions are violated, the results of the ANOVA may not be valid.
Sensitivity to Outliers: ANOVA can be sensitive to outliers. A single extreme value in one group can affect the sum of squares and consequently influence the F-statistic and the overall result of the test.
Dichotomous Variables: ANOVA is not suitable for dichotomous variables (variables that can take only two values, like yes/no or male/female). It is used to compare the means of groups for a continuous dependent variable.
Lack of Specificity: Although ANOVA can tell you that there is a significant difference between groups, it doesn’t tell you which specific groups are significantly different from each other. You need to carry out further post-hoc tests (like Tukey’s HSD or Bonferroni) for these pairwise comparisons.
Complexity with Multiple Factors: When dealing with multiple factors and interactions in factorial ANOVA, interpretation can become complex. The presence of interaction effects can make main effects difficult to interpret.
Requires Larger Sample Sizes: To detect an effect of a certain size, ANOVA generally requires larger sample sizes than a t-test.
Equal Group Sizes: While not always a strict requirement, ANOVA is most powerful and its assumptions are most likely to be met when groups are of equal or similar sizes.
About the author
Muhammad Hassan
Researcher, Academic Writer, Web developer
You may also like

Documentary Analysis – Methods, Applications and...

Textual Analysis – Types, Examples and Guide

Phenomenology – Methods, Examples and Guide

Methodological Framework – Types, Examples and...

Multidimensional Scaling – Types, Formulas and...

Uniform Histogram – Purpose, Examples and Guide
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
One Way ANOVA Overview & Example
By Jim Frost Leave a Comment
What is One Way ANOVA?
Use one way ANOVA to compare the means of three or more groups. This analysis is an inferential hypothesis test that uses samples to draw conclusions about populations. Specifically, it tells you whether your sample provides sufficient evidence to conclude that the groups’ population means are different. ANOVA stands for analysis of variance.
To perform one-way ANOVA, you’ll need a continuous dependent (outcome) variable and a categorical independent variable to form the groups.
For example, one-way ANOVA can determine whether parts made from four materials have different mean strengths.
In this post, learn about the hypotheses, assumptions, and interpreting the results for one-way ANOVA.
Related post : Descriptive vs. Inferential Statistics and Independent and Dependent Variables .
One Way ANOVA Hypotheses
One-way ANOVA has the following hypotheses:
- Null hypothesis: All population group means are equal.
- Alternative hypothesis : Not all population group means are equal.
Reject the null when your p-value is less than your significance level (e.g., 0.05). The differences between the means are statistically significant. Your sample provides sufficiently strong evidence to conclude that the population means are not all equal.
Note that one-way ANOVA is an omnibus test, providing overall results for your data. It tells you whether any group means are different—Yes or No. However, it doesn’t specify which pairs of means are different. To make that determination, follow up a statistically significant one-way ANOVA with a post hoc test that can identify specific group differences that are significant.
Related posts : Interpreting P Values and Null Hypothesis Definition .
One Way ANOVA Assumptions
For reliable one-way ANOVA results, your data should satisfy the following assumptions:
Use valid sampling methods
Use random sampling to help ensure your sample represents your target population. If your data do not reflect the population, your one-way ANOVA results will not be valid.
Additionally, the method assumes your sampling method obtains independent observations. Selecting one subject does not affect the chances of choosing any others.
Finally, the procedure uses independent samples. Each group contains a unique set of items.
Related posts : Representative Samples: Definition, Uses & Examples and Independent and Dependent Samples
Continuous data
One-way ANOVA requires continuous data . Typically, you quantity continuous variables using a scale that can be meaningfully divided into smaller fractions. For example, temperature, mass, length, and duration are continuous data.
Learn more about Hypothesis Tests for Continuous, Binary, and Count Data .
Data follows a normal distribution or each group has at least 15-20 observations
One-way ANOVA assumes your group data follow the normal distribution . However, your groups can be skewed if your sample size is large enough because of the central limit theorem.
Here are the sample size guidelines:
- 2 – 9 groups: At least 15 in each group.
- 10 – 12 groups: At least 20 per group.
For one-way ANOVA, unimodal data can be mildly skewed and the results will still be valid when all groups exceed the guidelines. Read here for more information about the simulation studies that support these sample size guidelines.
However, if your sample size is smaller, graph your data and determine whether the groups are skewed. If they are, you might need to use a nonparametric test . The Kruskal-Wallis test is the nonparametric test corresponding to one-way ANOVA.
Be sure to look for outliers because they can produce misleading results.
Related posts : Central Limit Theorem & Skewed Distributions
Groups can have equal or unequal variances but use the correct form of the test
One-way ANOVA has two methods for handling group variances. The traditional F-test ANOVA assumes that all groups have equal variances. On the other hand, Welch’s ANOVA does not assume they are equal. If in doubt, just use Welch’s ANOVA because it works well for either case.
Related posts : Variances and Standard Deviations
One Way ANOVA Example
Suppose we are a manufacturer testing four materials to make a part. We collect a random sample of parts made using the four materials and measure their strengths. Download the CSV dataset for this example: PostHocTests .
First, I’ll graph the data to see what we’re working with.

The bar chart shows differences between the group means. However, a graph doesn’t indicate whether those differences are due to chance during random sampling or reflect underlying population differences. One-way ANOVA can help us out with that!
Let’s use one-way ANOVA to determine whether the mean differences between these groups are statistically significant. Below are the statistical results.

The p-value of 0.004 is less than our significance level of 0.05. We reject the null and conclude that all four population means are not all equal. While the Means table shows the group means at the bottom, we don’t know which differences between pairs of groups are statistically significant.
To perform pairwise comparisons between these four groups, we need to use a post hoc test, also known as multiple comparisons. To continue with this example and find the significant group differences, read my post Using Post Hoc Tests with ANOVA .
Related posts : How to do One-Way ANOVA in Excel
Share this:

Reader Interactions
Comments and questions cancel reply.
What Is An ANOVA Test In Statistics: Analysis Of Variance
Julia Simkus
Editor at Simply Psychology
BA (Hons) Psychology, Princeton University
Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.
Learn about our Editorial Process
Saul Mcleod, PhD
Editor-in-Chief for Simply Psychology
BSc (Hons) Psychology, MRes, PhD, University of Manchester
Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.
On This Page:
An ANOVA test is a statistical test used to determine if there is a statistically significant difference between two or more categorical groups by testing for differences of means using a variance.
Another key part of ANOVA is that it splits the independent variable into two or more groups.
For example, one or more groups might be expected to influence the dependent variable, while the other group is used as a control group and is not expected to influence the dependent variable.

Assumptions of ANOVA
The assumptions of the ANOVA test are the same as the general assumptions for any parametric test:
- An ANOVA can only be conducted if there is no relationship between the subjects in each sample. This means that subjects in the first group cannot also be in the second group (e.g., independent samples/between groups).
- The different groups/levels must have equal sample sizes .
- An ANOVA can only be conducted if the dependent variable is normally distributed so that the middle scores are the most frequent and the extreme scores are the least frequent.
- Population variances must be equal (i.e., homoscedastic). Homogeneity of variance means that the deviation of scores (measured by the range or standard deviation, for example) is similar between populations.
Types of ANOVA Tests
There are different types of ANOVA tests. The two most common are a “One-Way” and a “Two-Way.”
The difference between these two types depends on the number of independent variables in your test.
One-way ANOVA
A one-way ANOVA (analysis of variance) has one categorical independent variable (also known as a factor) and a normally distributed continuous (i.e., interval or ratio level) dependent variable.
The independent variable divides cases into two or more mutually exclusive levels, categories, or groups.
The one-way ANOVA test for differences in the means of the dependent variable is broken down by the levels of the independent variable.
An example of a one-way ANOVA includes testing a therapeutic intervention (CBT, medication, placebo) on the incidence of depression in a clinical sample.
Note : Both the One-Way ANOVA and the Independent Samples t-Test can compare the means for two groups. However, only the One-Way ANOVA can compare the means across three or more groups.
P Value Calculator From F Ratio (ANOVA)
Two-way (factorial) ANOVA
A two-way ANOVA (analysis of variance) has two or more categorical independent variables (also known as a factor) and a normally distributed continuous (i.e., interval or ratio level) dependent variable.
The independent variables divide cases into two or more mutually exclusive levels, categories, or groups. A two-way ANOVA is also called a factorial ANOVA.
An example of factorial ANOVAs include testing the effects of social contact (high, medium, low), job status (employed, self-employed, unemployed, retired), and family history (no family history, some family history) on the incidence of depression in a population.
What are “Groups” or “Levels”?
In ANOVA, “groups” or “levels” refer to the different categories of the independent variable being compared.
For example, if the independent variable is “eggs,” the levels might be Non-Organic, Organic, and Free Range Organic. The dependent variable could then be the price per dozen eggs.
ANOVA F -value
The test statistic for an ANOVA is denoted as F . The formula for ANOVA is F = variance caused by treatment/variance due to random chance.
The ANOVA F value can tell you if there is a significant difference between the levels of the independent variable, when p < .05. So, a higher F value indicates that the treatment variables are significant.
Note that the ANOVA alone does not tell us specifically which means were different from one another. To determine that, we would need to follow up with multiple comparisons (or post-hoc) tests.
When the initial F test indicates that significant differences exist between group means, post hoc tests are useful for determining which specific means are significantly different when you do not have specific hypotheses that you wish to test.
Post hoc tests compare each pair of means (like t-tests), but unlike t-tests, they correct the significance estimate to account for the multiple comparisons.
What Does “Replication” Mean?
Replication requires a study to be repeated with different subjects and experimenters. This would enable a statistical analyzer to confirm a prior study by testing the same hypothesis with a new sample.
How to run an ANOVA?
For large datasets, it is best to run an ANOVA in statistical software such as R or Stata. Let’s refer to our Egg example above.
Non-Organic, Organic, and Free-Range Organic Eggs would be assigned quantitative values (1,2,3). They would serve as our independent treatment variable, while the price per dozen eggs would serve as the dependent variable. Other erroneous variables may include “Brand Name” or “Laid Egg Date.”
Using data and the aov() command in R, we could then determine the impact Egg Type has on the price per dozen eggs.
ANOVA vs. t-test?
T-tests and ANOVA tests are both statistical techniques used to compare differences in means and spreads of the distributions across populations.
The t-test determines whether two populations are statistically different from each other, whereas ANOVA tests are used when an individual wants to test more than two levels within an independent variable.
Referring back to our egg example, testing Non-Organic vs. Organic would require a t-test while adding in Free Range as a third option demands ANOVA.
Rather than generate a t-statistic, ANOVA results in an f-statistic to determine statistical significance.
What does anova stand for?
ANOVA stands for Analysis of Variance. It’s a statistical method to analyze differences among group means in a sample. ANOVA tests the hypothesis that the means of two or more populations are equal, generalizing the t-test to more than two groups.
It’s commonly used in experiments where various factors’ effects are compared. It can also handle complex experiments with factors that have different numbers of levels.
When to use anova?
ANOVA should be used when one independent variable has three or more levels (categories or groups). It’s designed to compare the means of these multiple groups.
What does an anova test tell you?
An ANOVA test tells you if there are significant differences between the means of three or more groups. If the test result is significant, it suggests that at least one group’s mean differs from the others. It does not, however, specify which groups are different from each other.
Why do you use chi-square instead of ANOVA?
You use the chi-square test instead of ANOVA when dealing with categorical data to test associations or independence between two categorical variables. In contrast, ANOVA is used for continuous data to compare the means of three or more groups.
ANOVA (Analysis of Variance)
ANOVA, short for Analysis of Variance, is a statistical method used to see if there are significant differences between the averages of three or more unrelated groups. This technique is especially useful when comparing more than two groups, which is a limitation of other tests like the t-test and z-test. For example, ANOVA can compare average IQ scores across several countries—like the US, Canada, Italy, and Spain—to see if nationality influences IQ scores. Ronald Fisher developed ANOVA in 1918, expanding the capabilities of previous tests by allowing for the comparison of multiple groups at once. This method is also referred to as Fisher’s analysis of variance, highlighting its ability to analyze how a categorical variable with multiple levels affects a continuous variable.
The use of ANOVA depends on the research design. Commonly, ANOVAs are used in three ways: one-way ANOVA , two-way ANOVA , and N-way ANOVA.
One-Way ANOVA
One-Way ANOVA is a statistical method used when we’re looking at the impact of one single factor on a particular outcome. For instance, if we want to explore how IQ scores vary by country, that’s where One-Way ANOVA comes into play. The “one way” part means we’re only considering one independent variable, which in this case is the country, but remember, this country variable can include any number of categories, from just two countries to twenty or more.
Two-Way ANOVA
Moving a step further, Two-Way ANOVA, also known as factorial ANOVA, allows us to examine the effect of two different factors on an outcome simultaneously. Building on our previous example, we could look at how both country and gender influence IQ scores. This method doesn’t just tell us about the individual effects of each factor but also lets us explore interactions between them. An interaction effect means the impact of one factor might change depending on the level of the other factor. For example, the difference in IQ scores between genders might vary from one country to another, suggesting that the effect of gender on IQ is not consistent across all countries.
N-Way ANOVA
When researchers have more than two factors to consider, they turn to N-Way ANOVA, where “n” represents the number of independent variables in the analysis. This could mean examining how IQ scores are influenced by a combination of factors like country, gender, age group, and ethnicity all at once. N-Way ANOVA allows for a comprehensive analysis of how these multiple factors interact with each other and their combined effect on the dependent variable, providing a deeper understanding of the dynamics at play.
In summary, ANOVA is a versatile statistical tool that scales from analyzing the effect of one factor (One-Way ANOVA) to multiple factors (Two-Way or N-Way ANOVA) on an outcome. By using ANOVA, researchers can uncover not just the direct effects of independent variables on a dependent variable but also how these variables interact with each other, offering rich insights into complex phenomena.
Looking for assistance with your research?
Schedule a time to speak with an expert using the calendar below.
User-friendly Software
Transform raw data to written interpreted results in seconds.
General Purpose and Procedure
Omnibus ANOVA test:
The null hypothesis for an ANOVA is that there is no significant difference among the groups. The alternative hypothesis assumes that there is at least one significant difference among the groups. After cleaning the data, the researcher must test the assumptions of ANOVA. They must then calculate the F -ratio and the associated probability value ( p -value). In general, if the p -value associated with the F is smaller than .05, then the null hypothesis is rejected and the alternative hypothesis is supported. If the null hypothesis is rejected, one concludes that the means of all the groups are not equal. Post-hoc tests tell the researcher which groups are different from each other.
So what if you find statistical significance? Multiple comparison tests
When you conduct an ANOVA, you are attempting to determine if there is a statistically significant difference among the groups. If you find that there is a difference, you will then need to examine where the group differences lay.
At this point you could run post-hoc tests which are t tests examining mean differences between the groups. There are several multiple comparison tests that can be conducted that will control for Type I error rate, including the Bonferroni , Scheffe, Dunnet, and Tukey tests.
Research Questions the ANOVA Examines
One-way ANOVA: Are there differences in GPA by grade level (freshmen vs. sophomores vs. juniors)?
Two-way ANOVA: Are there differences in GPA by grade level (freshmen vs. sophomores vs. juniors) and gender (male vs. female)?
Data Level and Assumptions
The level of measurement of the variables and assumptions of the test play an important role in ANOVA. In ANOVA, the dependent variable must be a continuous (interval or ratio) level of measurement. The independent variables in ANOVA must be categorical (nominal or ordinal) variables. Like the t -test, ANOVA is also a parametric test and has some assumptions. ANOVA assumes that the data is normally distributed. The ANOVA also assumes homogeneity of variance, which means that the variance among the groups should be approximately equal. ANOVA also assumes that the observations are independent of each other. Researchers should keep in mind when planning any study to look out for extraneous or confounding variables. ANOVA has methods (i.e., ANCOVA) to control for confounding variables.
Testing of the Assumptions
- The population from which samples are drawn should be normally distributed.
- Independence of cases: the sample cases should be independent of each other.
- Homogeneity of variance: Homogeneity means that the variance among the groups should be approximately equal.
These assumptions can be tested using statistical software (like Intellectus Statistics!). The assumption of homogeneity of variance can be tested using tests such as Levene’s test or the Brown-Forsythe Test. Normality of the distribution of the scores can be tested using histograms, the values of skewness and kurtosis, or using tests such as Shapiro-Wilk or Kolmogorov-Smirnov. The assumption of independence can be determined from the design of the study.
It is important to note that ANOVA is not robust to violations to the assumption of independence. This is to say, that even if you violate the assumptions of homogeneity or normality, you can conduct the test and basically trust the findings. However, the results of the ANOVA are invalid if the independence assumption is violated. In general, with violations of homogeneity the analysis is considered robust if you have equal sized groups. With violations of normality, continuing with the ANOVA is generally ok if you have a large sample size .
Related Analyses: MANOVA and ANCOVA
Researchers have extended ANOVA in MANOVA and ANCOVA. MANOVA stands for the multivariate analysis of variance. MANOVA is used when there are two or more dependent variables. ANCOVA is the term for analysis of covariance. The ANCOVA is used when the researcher includes one or more covariate variables in the analysis.
Need more help?
Check out our online course for conducting an ANOVA here .
Algina, J., & Olejnik, S. (2003). Conducting power analyses for ANOVA and ANCOVA in between-subjects designs. Evaluation & the Health Professions, 26 (3), 288-314.
Cardinal, R. N., & Aitken, M. R. F. (2006). ANOVA for the behavioural sciences researcher . Mahwah, NJ: Lawrence Erlbaum Associates.
Davison, M. L., & Sharma, A. R. (1994). ANOVA and ANCOVA of pre- and post-test, ordinal data. Psychometrika, 59 (4), 593-600.
Levy, M. S., & Neill, J. W. (1990). Testing for lack of fit in linear multiresponse models based on exact or near replicates. Communications in Statistics – Theory and Methods, 19 (6), 1987-2002.
Tsangari, H., & Akritas, M. G. (2004). Nonparametric ANCOVA with two and three covariates. Journal of Multivariate Analysis, 88 (2), 298-319.
Turner, J. R., & Thayer, J. F. (2001). Introduction to analysis of variance: Design, analysis, & interpretation . Thousand Oaks, CA: Sage Publications.
Wilcox, R. R. (2005). An approach to ANCOVA that allows multiple covariates, nonlinearity, and heteroscedasticity. Educational and Psychological Measurement, 65 (3), 442-450.
Wright, D. B. (2006). Comparing groups in a before-after design: When t test and ANCOVA produce different results. British Journal of Educational Psychology, 76 , 663-675.
To Reference this Page : Statistics Solutions. (2013). ANOVA . Retrieved from https://www.statisticssolutions.com/free-resources/directory-of-statistical-analyses/anova/
Related Pages:
- Conduct and Interpret a One-Way ANOVA
- Conduct and Interpret a Factorial ANOVA
- Conduct and Interpret a Repeated Measures ANOVA
Statistics Solutions can assist with your quantitative analysis by assisting you to develop your methodology and results chapters. The services that we offer include:
Data Analysis Plan
- Edit your research questions and null/alternative hypotheses
- Write your data analysis plan; specify specific statistics to address the research questions, the assumptions of the statistics, and justify why they are the appropriate statistics; provide references
- Justify your sample size/power analysis, provide references
- Explain your data analysis plan to you so you are comfortable and confident
- Two hours of additional support with your statistician
Quantitative Results Section (Descriptive Statistics, Bivariate and Multivariate Analyses, Structural Equation Modeling , Path analysis, HLM, Cluster Analysis )
- Clean and code dataset
- Conduct descriptive statistics (i.e., mean, standard deviation, frequency and percent, as appropriate)
- Conduct analyses to examine each of your research questions
- Write-up results
- Provide APA 7 th edition tables and figures
- Explain Chapter 4 findings
- Ongoing support for entire results chapter statistics
Please call 727-442-4290 to request a quote based on the specifics of your research, schedule using the calendar on this page, or email [email protected]
Module 13: F-Distribution and One-Way ANOVA
One-way anova, learning outcomes.
- Conduct and interpret one-way ANOVA
The purpose of a one-way ANOVA test is to determine the existence of a statistically significant difference among several group means. The test actually uses variances to help determine if the means are equal or not. In order to perform a one-way ANOVA test, there are five basic assumptions to be fulfilled:
- Each population from which a sample is taken is assumed to be normal.
- All samples are randomly selected and independent.
- The populations are assumed to have equal standard deviations (or variances) .
- The factor is a categorical variable.
- The response is a numerical variable.
The Null and Alternative Hypotheses
The null hypothesis is simply that all the group population means are the same. The alternative hypothesis is that at least one pair of means is different. For example, if there are k groups:
H 0 : μ 1 = μ 2 = μ 3 = … = μ k
H a : At least two of the group means μ 1 , μ 2 , μ 3 , …, μ k are not equal.
The graphs, a set of box plots representing the distribution of values with the group means indicated by a horizontal line through the box, help in the understanding of the hypothesis test. In the first graph (red box plots), H 0 : μ 1 = μ 2 = μ 3 and the three populations have the same distribution if the null hypothesis is true. The variance of the combined data is approximately the same as the variance of each of the populations.
If the null hypothesis is false, then the variance of the combined data is larger which is caused by the different means as shown in the second graph (green box plots).

(b) H 0 is not true. All means are not the same; the differences are too large to be due to random variation.
Concept Review
Analysis of variance extends the comparison of two groups to several, each a level of a categorical variable (factor). Samples from each group are independent, and must be randomly selected from normal populations with equal variances. We test the null hypothesis of equal means of the response in every group versus the alternative hypothesis of one or more group means being different from the others. A one-way ANOVA hypothesis test determines if several population means are equal. The distribution for the test is the F distribution with two different degrees of freedom.
Assumptions:
- The populations are assumed to have equal standard deviations (or variances).
- OpenStax, Statistics, One-Way ANOVA. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution
- Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
- Completing a simple ANOVA table. Authored by : masterskills. Located at : https://youtu.be/OXA-bw9tGfo . License : All Rights Reserved . License Terms : Standard YouTube License

Hypothesis Testing - Analysis of Variance (ANOVA)
- 1
- | 2
- | 3
- | 4
- | 5

The ANOVA Approach
Test statistic for anova.

All Modules

Table of F-Statistic Values
Consider an example with four independent groups and a continuous outcome measure. The independent groups might be defined by a particular characteristic of the participants such as BMI (e.g., underweight, normal weight, overweight, obese) or by the investigator (e.g., randomizing participants to one of four competing treatments, call them A, B, C and D). Suppose that the outcome is systolic blood pressure, and we wish to test whether there is a statistically significant difference in mean systolic blood pressures among the four groups. The sample data are organized as follows:
|
|
|
|
|
|
|---|---|---|---|---|
|
| n | n | n | n |
|
|
|
|
|
|
|
| s | s | s | s |
The hypotheses of interest in an ANOVA are as follows:
- H 0 : μ 1 = μ 2 = μ 3 ... = μ k
- H 1 : Means are not all equal.
where k = the number of independent comparison groups.
In this example, the hypotheses are:
- H 0 : μ 1 = μ 2 = μ 3 = μ 4
- H 1 : The means are not all equal.
The null hypothesis in ANOVA is always that there is no difference in means. The research or alternative hypothesis is always that the means are not all equal and is usually written in words rather than in mathematical symbols. The research hypothesis captures any difference in means and includes, for example, the situation where all four means are unequal, where one is different from the other three, where two are different, and so on. The alternative hypothesis, as shown above, capture all possible situations other than equality of all means specified in the null hypothesis.
The test statistic for testing H 0 : μ 1 = μ 2 = ... = μ k is:
and the critical value is found in a table of probability values for the F distribution with (degrees of freedom) df 1 = k-1, df 2 =N-k. The table can be found in "Other Resources" on the left side of the pages.
NOTE: The test statistic F assumes equal variability in the k populations (i.e., the population variances are equal, or s 1 2 = s 2 2 = ... = s k 2 ). This means that the outcome is equally variable in each of the comparison populations. This assumption is the same as that assumed for appropriate use of the test statistic to test equality of two independent means. It is possible to assess the likelihood that the assumption of equal variances is true and the test can be conducted in most statistical computing packages. If the variability in the k comparison groups is not similar, then alternative techniques must be used.
The F statistic is computed by taking the ratio of what is called the "between treatment" variability to the "residual or error" variability. This is where the name of the procedure originates. In analysis of variance we are testing for a difference in means (H 0 : means are all equal versus H 1 : means are not all equal) by evaluating variability in the data. The numerator captures between treatment variability (i.e., differences among the sample means) and the denominator contains an estimate of the variability in the outcome. The test statistic is a measure that allows us to assess whether the differences among the sample means (numerator) are more than would be expected by chance if the null hypothesis is true. Recall in the two independent sample test, the test statistic was computed by taking the ratio of the difference in sample means (numerator) to the variability in the outcome (estimated by Sp).
The decision rule for the F test in ANOVA is set up in a similar way to decision rules we established for t tests. The decision rule again depends on the level of significance and the degrees of freedom. The F statistic has two degrees of freedom. These are denoted df 1 and df 2 , and called the numerator and denominator degrees of freedom, respectively. The degrees of freedom are defined as follows:
df 1 = k-1 and df 2 =N-k,
where k is the number of comparison groups and N is the total number of observations in the analysis. If the null hypothesis is true, the between treatment variation (numerator) will not exceed the residual or error variation (denominator) and the F statistic will small. If the null hypothesis is false, then the F statistic will be large. The rejection region for the F test is always in the upper (right-hand) tail of the distribution as shown below.
Rejection Region for F Test with a =0.05, df 1 =3 and df 2 =36 (k=4, N=40)

For the scenario depicted here, the decision rule is: Reject H 0 if F > 2.87.
return to top | previous page | next page
Content ©2019. All Rights Reserved. Date last modified: January 23, 2019. Wayne W. LaMorte, MD, PhD, MPH

Understanding the Null Hypothesis for ANOVA Models
A one-way ANOVA is used to determine if there is a statistically significant difference between the mean of three or more independent groups.
A one-way ANOVA uses the following null and alternative hypotheses:
- H 0 : μ 1 = μ 2 = μ 3 = … = μ k (all of the group means are equal)
- H A : At least one group mean is different from the rest
To decide if we should reject or fail to reject the null hypothesis, we must refer to the p-value in the output of the ANOVA table.
If the p-value is less than some significance level (e.g. 0.05) then we can reject the null hypothesis and conclude that not all group means are equal.
A two-way ANOVA is used to determine whether or not there is a statistically significant difference between the means of three or more independent groups that have been split on two variables (sometimes called “factors”).
A two-way ANOVA tests three null hypotheses at the same time:
- All group means are equal at each level of the first variable
- All group means are equal at each level of the second variable
- There is no interaction effect between the two variables
To decide if we should reject or fail to reject each null hypothesis, we must refer to the p-values in the output of the two-way ANOVA table.
The following examples show how to decide to reject or fail to reject the null hypothesis in both a one-way ANOVA and two-way ANOVA.
Example 1: One-Way ANOVA
Suppose we want to know whether or not three different exam prep programs lead to different mean scores on a certain exam. To test this, we recruit 30 students to participate in a study and split them into three groups.
The students in each group are randomly assigned to use one of the three exam prep programs for the next three weeks to prepare for an exam. At the end of the three weeks, all of the students take the same exam.
The exam scores for each group are shown below:

When we enter these values into the One-Way ANOVA Calculator , we receive the following ANOVA table as the output:

Notice that the p-value is 0.11385 .
For this particular example, we would use the following null and alternative hypotheses:
- H 0 : μ 1 = μ 2 = μ 3 (the mean exam score for each group is equal)
Since the p-value from the ANOVA table is not less than 0.05, we fail to reject the null hypothesis.
This means we don’t have sufficient evidence to say that there is a statistically significant difference between the mean exam scores of the three groups.
Example 2: Two-Way ANOVA
Suppose a botanist wants to know whether or not plant growth is influenced by sunlight exposure and watering frequency.
She plants 40 seeds and lets them grow for two months under different conditions for sunlight exposure and watering frequency. After two months, she records the height of each plant. The results are shown below:

In the table above, we see that there were five plants grown under each combination of conditions.
For example, there were five plants grown with daily watering and no sunlight and their heights after two months were 4.8 inches, 4.4 inches, 3.2 inches, 3.9 inches, and 4.4 inches:

She performs a two-way ANOVA in Excel and ends up with the following output:

We can see the following p-values in the output of the two-way ANOVA table:
- The p-value for watering frequency is 0.975975 . This is not statistically significant at a significance level of 0.05.
- The p-value for sunlight exposure is 3.9E-8 (0.000000039) . This is statistically significant at a significance level of 0.05.
- The p-value for the interaction between watering frequency and sunlight exposure is 0.310898 . This is not statistically significant at a significance level of 0.05.
These results indicate that sunlight exposure is the only factor that has a statistically significant effect on plant height.
And because there is no interaction effect, the effect of sunlight exposure is consistent across each level of watering frequency.
That is, whether a plant is watered daily or weekly has no impact on how sunlight exposure affects a plant.
Additional Resources
The following tutorials provide additional information about ANOVA models:
How to Interpret the F-Value and P-Value in ANOVA How to Calculate Sum of Squares in ANOVA What Does a High F Value Mean in ANOVA?
Featured Posts
Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.
2 Replies to “Understanding the Null Hypothesis for ANOVA Models”
Hi, I’m a student at Stellenbosch University majoring in Conservation Ecology and Entomology and we are currently busy doing stats. I am still at a very entry level of stats understanding, so pages like these are of huge help. I wanted to ask, why is the sum of squares (treatment) for the one way ANOVA so high? I calculated it by hand and got a much lower number, could you please help point out if and where I went wrong?
As I understand it, SSB (treatment) is calculated by finding the mean of each group and the grand mean, and then calculating the sum of squares like this: GM = 85.5 x1 = 83.4 x2 = 89.3 x3 = 84.7
SSB = (85.5 – 83.4)^2 + (85.5 – 89.3)^2 + (85.5 – 84.7)^2 = 18.65 DF = 2
I would appreciate any help, thank you so much!
Hi Theo…Certainly! Here are the equations rewritten as they would be typed in Python:
### Sum of Squares Between Groups (SSB)
In a one-way ANOVA, the sum of squares between groups (SSB) measures the variation due to the interaction between the groups. It is calculated as follows:
1. **Calculate the group means**: “`python mean_group1 = 83.4 mean_group2 = 89.3 mean_group3 = 84.7 “`
2. **Calculate the grand mean**: “`python grand_mean = 85.5 “`
3. **Calculate the sum of squares between groups (SSB)**: Assuming each group has `n` observations: “`python n = 10 # Number of observations in each group
ssb = n * ((mean_group1 – grand_mean)**2 + (mean_group2 – grand_mean)**2 + (mean_group3 – grand_mean)**2) “`
### Example Calculation
For simplicity, let’s assume each group has 10 observations: “`python n = 10
ssb = n * ((83.4 – 85.5)**2 + (89.3 – 85.5)**2 + (84.7 – 85.5)**2) “`
Now calculate each term: “`python term1 = (83.4 – 85.5)**2 # term1 = (-2.1)**2 = 4.41 term2 = (89.3 – 85.5)**2 # term2 = (3.8)**2 = 14.44 term3 = (84.7 – 85.5)**2 # term3 = (-0.8)**2 = 0.64 “`
Sum these squared differences: “`python sum_of_squared_diffs = term1 + term2 + term3 # sum_of_squared_diffs = 4.41 + 14.44 + 0.64 = 19.49 ssb = n * sum_of_squared_diffs # ssb = 10 * 19.49 = 194.9 “`
So, the sum of squares between groups (SSB) is 194.9, assuming each group has 10 observations.
### Degrees of Freedom (DF)
The degrees of freedom for SSB is calculated as: “`python df_between = k – 1 “` where `k` is the number of groups.
For three groups: “`python k = 3 df_between = k – 1 # df_between = 3 – 1 = 2 “`
### Summary
– **SSB** should consider the number of observations in each group. – **DF** is the number of groups minus one.
By ensuring you include the number of observations per group in your SSB calculation, you can get the correct SSB value.
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Join the Statology Community
Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!
By subscribing you accept Statology's Privacy Policy.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
11.4 One-Way ANOVA and Hypothesis Tests for Three or More Population Means
Learning objectives.
- Conduct and interpret hypothesis tests for three or more population means using one-way ANOVA.
The purpose of a one-way ANOVA (analysis of variance) test is to determine the existence of a statistically significant difference among the means of three or more populations. The test actually uses variances to help determine if the population means are equal or not.
Throughout this section, we will use subscripts to identify the values for the means, sample sizes, and standard deviations for the populations:
| [latex]\mu_k[/latex] | |
| [latex]\sigma_k[/latex] | |
| [latex]n_k[/latex] | |
| [latex]\overline{x}_k[/latex] | |
| [latex]s_k[/latex] |
[latex]k[/latex] is the number of populations under study, [latex]n[/latex] is the total number of observations in all of the samples combined, and [latex]\overline{\overline{x}}[/latex] is the mean of the sample means.
[latex]\begin{eqnarray*} n & = & n_1+n_2+\cdots+n_k \\ \\ \overline{\overline{x}} & = & \frac{n_1 \times \overline{x}_1 +n_2 \times \overline{x}_2 +\cdots+n_k \times \overline{x}_k}{n} \end{eqnarray*}[/latex]
One-Way ANOVA
A predictor variable is called a factor or independent variable . For example age, temperature, and gender are factors. The groups or samples are often referred to as treatments . This terminology comes from the use of ANOVA procedures in medical and psychological research to determine if there is a difference in the effects of different treatments.
A local college wants to compare the mean GPA for players on four of its sports teams: basketball, baseball, hockey, and lacrosse. A random sample of players was taken from each team and their GPA recorded in the table below.
| 3.6 | 2.1 | 4.0 | 2.0 |
| 2.9 | 2.6 | 2.0 | 3.6 |
| 2.5 | 3.9 | 2.6 | 3.9 |
| 3.3 | 3.1 | 3.2 | 2.7 |
| 3.8 | 3.4 | 3.2 | 2.5 |
In this example, the factor is the sports team.
| 5 | 5 | 5 | 5 | |
| 3.22 | 3.02 | 3 | 2.94 |
[latex]\begin{eqnarray*} k & = & 4 \\ \\ n & = & n_1+n_2+n_3+n_4 \\ & = & 5+5+5+5 \\ & = & 20 \\ \\ \overline{\overline{x}} & = & \frac{n_1 \times \overline{x}_1+n_2 \times \overline{x}_2+n_3 \times \overline{x}_3+n_4 \times \overline{x}_4}{n} \\ & = & \frac{5 \times 3.22+5 \times 3.02+5 \times 3+5 \times 2.94}{20} \\& = & 3.045 \end{eqnarray*}[/latex]
The following assumptions are required to use a one-way ANOVA test:
- Each population from which a sample is taken is normally distributed.
- All samples are randomly selected and independently taken from the populations.
- The populations are assumed to have equal variances.
- The population data is numerical (interval or ratio level).
The logic behind one-way ANOVA is to compare population means based on two independent estimates of the (assumed) equal variance [latex]\sigma^2[/latex] between the populations:
- One estimate of the equal variance [latex]\sigma^2[/latex] is based on the variability among the sample means themselves (called the between-groups estimate of population variance).
- One estimate of the equal variance [latex]\sigma^2[/latex] is based on the variability of the data within each sample (called the within-groups estimate of population variance).
The one-way ANOVA procedure compares these two estimates of the population variance [latex]\sigma^2[/latex] to determine if the population means are equal or if there is a difference in the population means. Because ANOVA involves the comparison of two estimates of variance, an [latex]F[/latex]-distribution is used to conduct the ANOVA test. The test statistic is an [latex]F[/latex]-score that is the ratio of the two estimates of population variance:
[latex]\displaystyle{F=\frac{\mbox{variance between groups}}{\mbox{variance within groups}}}[/latex]
The degrees of freedom for the [latex]F[/latex]-distribution are [latex]df_1=k-1[/latex] and [latex]df_2=n-k[/latex] where [latex]k[/latex] is the number of populations and [latex]n[/latex] is the total number of observations in all of the samples combined.
The variance between groups estimate of the population variance is called the mean square due to treatment , [latex]MST[/latex]. The [latex]MST[/latex] is the estimate of the population variance determined by the variance of the sample means from the overall sample mean [latex]\overline{\overline{x}}[/latex]. When the population means are equal, [latex]MST[/latex] provides an unbiased estimate of the population variance. When the population means are not equal, [latex]MST[/latex] provides an overestimate of the population variance.
[latex]\begin{eqnarray*} SST & = & n_1 \times (\overline{x}_1-\overline{\overline{x}})^2+n_2\times (\overline{x}_2-\overline{\overline{x}})^2+ \cdots +n_k \times (\overline{x}_k-\overline{\overline{x}})^2 \\ \\ MST & =& \frac{SST}{k-1} \end{eqnarray*}[/latex]
The variance within groups estimate of the population variance is called the mean square due to error , [latex]MSE[/latex]. The [latex]MSE[/latex] is the pooled estimate of the population variance using the sample variances as estimates for the population variance. The [latex]MSE[/latex] always provides an unbiased estimate of the population variance because it is not affected by whether or not the population means are equal.
[latex]\begin{eqnarray*} SSE & = & (n_1-1) \times s_1^2+ (n_2-1) \times s_2^2+ \cdots + (n_k-1) \times s_k^2\\ \\ MSE & =& \frac{SSE}{n -k} \end{eqnarray*}[/latex]
The one-way ANOVA test depends on the fact that the variance between groups [latex]MST[/latex] is influenced by differences between the population means, which results in [latex]MST[/latex] being either an unbiased or overestimate of the population variance. Because the variance within groups [latex]MSE[/latex] compares values of each group to its own group mean, [latex]MSE[/latex] is not affected by differences between the population means and is always an unbiased estimate of the population variance.
The null hypothesis in a one-way ANOVA test is that the population means are all equal and the alternative hypothesis is that there is a difference in the population means. The [latex]F[/latex]-score for the one-way ANOVA test is [latex]\displaystyle{F=\frac{MST}{MSE}}[/latex] with [latex]df_1=k-1[/latex] and [latex]df_2=n-k[/latex]. The p -value for the test is the area in the right tail of the [latex]F[/latex]-distribution, to the right of the [latex]F[/latex]-score.
- When the variance between groups [latex]MST[/latex] and variance within groups [latex]MSE[/latex] are close in value, the [latex]F[/latex]-score is close to 1 and results in a large p -value. In this case, the conclusion is that the population means are equal.
- When the variance between groups [latex]MST[/latex] is significantly larger than the variability within groups [latex]MSE[/latex], the [latex]F[/latex]-score is large and results in a small p -value. In this case, the conclusion is that there is a difference in the population means.
Steps to Conduct a Hypothesis Test for Three or More Population Means
- Verify that the one-way ANOVA assumptions are met.
[latex]\begin{eqnarray*} \\ H_0: & & \mu_1=\mu_2=\cdots=\mu_k\end{eqnarray*}[/latex].
[latex]\begin{eqnarray*} \\ H_a: & & \mbox{at least one population mean is different from the others} \\ \\ \end{eqnarray*}[/latex]
- Collect the sample information for the test and identify the significance level [latex]\alpha[/latex].
[latex]\begin{eqnarray*}F & = & \frac{MST}{MSE} \\ \\ df_1 & = & k-1 \\ \\ df_2 & = & n-k \\ \\ \end{eqnarray*}[/latex]
- The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
- The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
- Write down a concluding sentence specific to the context of the question.
Assume the populations are normally distributed and have equal variances. At the 5% significance level, is there a difference in the average GPA between the sports team.
Let basketball be population 1, let baseball be population 2, let hockey be population 3, and let lacrosse be population 4. From the question we have the following information:
| [latex]n_1=5[/latex] | [latex]n_2=5[/latex] | [latex]n_3=5[/latex] | [latex]n_4=5[/latex] |
| [latex]\overline{x}_1=3.22[/latex] | [latex]\overline{x}_2=3.02[/latex] | [latex]\overline{x}_3=3[/latex] | [latex]\overline{x}_4=2.94[/latex] |
| [latex]s_1^2=0.277[/latex] | [latex]s_2^2=0.487[/latex] | [latex]s_3^2=0.56[/latex] | [latex]s_4^2=0.613[/latex] |
Previously, we found [latex]k=4[/latex], [latex]n=20[/latex], and [latex]\overline{\overline{x}}=3.045[/latex].
Hypotheses:
[latex]\begin{eqnarray*} H_0: & & \mu_1=\mu_2=\mu_3=\mu_4 \\ H_a: & & \mbox{at least one population mean is different from the others} \end{eqnarray*}[/latex]
To calculate out the [latex]F[/latex]-score, we need to find [latex]MST[/latex] and [latex]MSE[/latex].
[latex]\begin{eqnarray*} SST & = & n_1 \times (\overline{x}_1-\overline{\overline{x}})^2+n_2\times (\overline{x}_2-\overline{\overline{x}})^2+n_3 \times (\overline{x}_3-\overline{\overline{x}})^2 +n_4 \times (\overline{x}_4-\overline{\overline{x}})^2\\ & = & 5 \times (3.22-3.045)^2+5 \times (3.02-3.045)^2+5 \times (3-3.045)^2 \\ & & +5 \times (2.94 -3.045)^2 \\ & = & 0.2215 \\ \\ MST & = & \frac{SST}{k-1} \\ & = & \frac{0.2215 }{4-1} \\ & = & 0.0738...\\ \\ SSE & = & (n_1-1) \times s_1^2+ (n_2-1) \times s_2^2+ (n_3-1) \times s_3^2+ (n_4-1) \times s_4^2\\ & = &( 5-1) \times 0.277+(5-1) \times 0.487+(5-1) \times 0.56 +(5-1)\times 0.623 \\ & = & 7.788 \\ \\ MSE & = & \frac{SSE}{n-k} \\ & = & \frac{7.788 }{20-4} \\ & = & 0.48675\end{eqnarray*}[/latex]
The p -value is the area in the right tail of the [latex]F[/latex]-distribution. To use the f.dist.rt function, we need to calculate out the [latex]F[/latex]-score and the degrees of freedom:
[latex]\begin{eqnarray*} F & = &\frac{MST}{MSE} \\ & = & \frac{0.0738...}{0.48675} \\ & = & 0.15168... \\ \\ df_1 & = & k-1 \\ & = & 4-1 \\ & = & 3 \\ \\df_2 & = & n-k \\ & = & 20-4 \\ & = & 16\end{eqnarray*}[/latex]
| f.dist.rt | ||
| 0.15168… | 0.9271 | |
| 3 | ||
| 16 |
So the p -value[latex]=0.9271[/latex].
Conclusion:
Because p -value[latex]=0.9271 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is enough evidence to suggest that the mean GPA for the sports teams are the same.
- The null hypothesis [latex]\mu_1=\mu_2=\mu_3=\mu_4[/latex] is the claim that the mean GPA for the sports teams are all equal.
- The alternative hypothesis is the claim that at least one of the population means is not equal to the others. The alternative hypothesis does not say that all of the population means are not equal, only that at least one of them is not equal to the others.
- The function is f.dist.rt because we are finding the area in the right tail of an [latex]F[/latex]-distribution.
- Field 1 is the value of [latex]F[/latex].
- Field 2 is the value of [latex]df_1[/latex].
- Field 3 is the value of [latex]df_2[/latex].
- The p -value of 0.9271 is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the population means are all equal.
ANOVA Summary Tables
The calculation of the [latex]MST[/latex], [latex]MSE[/latex], and the [latex]F[/latex]-score for a one-way ANOVA test can be time consuming, even with the help of software like Excel. However, Excel has a built-in one-way ANOVA summary table that not only generates the averages, variances, [latex]MST[/latex] and [latex]MSE[/latex], but also calculates the required [latex]F[/latex]-score and p -value for the test.
USING EXCEL TO CREATE A ONE-WAY ANOVA SUMMARY TABLE
In order to create a one-way ANOVA summary table, we need to use the Analysis ToolPak. Follow these instructions to add the Analysis ToolPak.
- Enter the data into an Excel worksheet.
- Go to the Data tab and click on Data Analysis . If you do not see Data Analysis in the Data tab, you will need to install the Analysis ToolPak.
- In the Data Analysis window, select Anova: Single Factor . Click OK .
- In the Inpu t range, enter the cell range for the data.
- In the Grouped By box, select rows if your data is entered as rows (the default is columns).
- Click on Labels in first row if the you included the column headings in the input range.
- In the Alpha box, enter the significance level for the test.
- From the Output Options , select the location where you want the output to appear.
This website provides additional information on using Excel to create a one-way ANOVA summary table.
Because we are using the p -value approach to hypothesis testing, it is not crucial that we enter the actual significance level we are using for the test. The p -value (the area in the right tail of the [latex]F[/latex]-distribution) is not affected by significance level. For the critical-value approach to hypothesis testing, we must enter the correct significance level for the test because the critical value does depend on the significance level.
Let basketball be population 1, let baseball be population 2, let hockey be population 3, and let lacrosse be population 4.
The ANOVA summary table generated by Excel is shown below:
| Basketball | 5 | 16.1 | 3.22 | 0.277 | ||
| Baseball | 5 | 15.1 | 3.02 | 0.487 | ||
| Hockey | 5 | 15 | 3 | 0.56 | ||
| Lacrosse | 5 | 14.7 | 2.94 | 0.623 | ||
| Between Groups | 0.2215 | 3 | 0.073833 | 0.151686 | 0.927083 | 3.238872 |
| Within Groups | 7.788 | 16 | 0.48675 | |||
| Total | 8.0095 | 19 |
The p -value for the test is in the P -value column of the between groups row . So the p -value[latex]=0.9271[/latex].
- In the top part of the ANOVA summary table (under the Summary heading), we have the averages and variances for each of the groups (basketball, baseball, hockey, and lacrosse).
- The value of [latex]SST[/latex] (in the SS column of the between groups row).
- The value of [latex]MST[/latex] (in the MS column of the between group s row).
- The value of [latex]SSE[/latex] (in the SS column of the within groups row).
- The value of [latex]MSE[/latex] (in the MS column of the within groups row).
- The value of the [latex]F[/latex]-score (in the F column of the between groups row).
- The p -value (in the p -value column of the between groups row).
A fourth grade class is studying the environment. One of the assignments is to grow bean plants in different soils. Tommy chose to grow his bean plants in soil found outside his classroom mixed with dryer lint. Tara chose to grow her bean plants in potting soil bought at the local nursery. Nick chose to grow his bean plants in soil from his mother’s garden. No chemicals were used on the plants, only water. They were grown inside the classroom next to a large window. Each child grew five plants. At the end of the growing period, each plant was measured, producing the data (in inches) in the table below.
| 24 | 25 | 23 |
| 21 | 31 | 27 |
| 23 | 23 | 22 |
| 30 | 20 | 30 |
| 23 | 28 | 20 |
Assume the heights of the plants are normally distribution and have equal variance. At the 5% significance level, does it appear that the three media in which the bean plants were grown produced the same mean height?
Let Tommy’s plants be population 1, let Tara’s plants be population 2, and let Nick’s plants be population 3.
[latex]\begin{eqnarray*} H_0: & & \mu_1=\mu_2=\mu_3 \\ H_a: & & \mbox{at least one population mean is different from the others} \end{eqnarray*}[/latex]
| Tommy’s Plants | 5 | 121 | 24.2 | 11.7 | ||
| Tara’s Plants | 5 | 127 | 25.4 | 18.3 | ||
| Nick’s Plants | 5 | 122 | 24.4 | 16.3 | ||
| Between Groups | 4.133333 | 2 | 2.066667 | 0.133909 | 0.875958 | 3.885294 |
| Within Groups | 185.2 | 12 | 15.43333 | |||
| Total | 189.3333 | 14 |
So the p -value[latex]=0.8760[/latex].
Because p -value[latex]=0.8760 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is enough evidence to suggest that the mean heights of the plants grown in three media are the same.
- The null hypothesis [latex]\mu_1=\mu_2=\mu_3[/latex] is the claim that the mean heights of the plants grown in the three different media are all equal.
- The p -value of 0.8760 is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the population means are all equal.
A statistics professor wants to study the average GPA of students in four different programs: marketing, management, accounting, and human resources. The professor took a random sample of GPAs of students in those programs at the end of the past semester. The data is recorded in the table below.
| 2.17 | 2.63 | 3.21 | 3.27 |
| 1.85 | 1.77 | 3.78 | 3.45 |
| 2.83 | 3.25 | 4.00 | 2.85 |
| 1.69 | 1.86 | 2.95 | 2.26 |
| 3.33 | 2.21 | 2.65 | 3.18 |
Assume the GPAs of the students are normally distributed and have equal variance. At the 5% significance level, is there a difference in the average GPA of the students in the different programs?
Let marketing be population 1, let management be population 2, let accounting be population 3, and let human resources be population 4.
[latex]\begin{eqnarray*} H_0: & & \mu_1=\mu_2=\mu_3=\mu_4\\ H_a: & & \mbox{at least one population mean is different from the others} \end{eqnarray*}[/latex]
| Marketing | 5 | 11.87 | 2.374 | 0.47648 | ||
| Management | 5 | 11.72 | 2.344 | 0.37108 | ||
| Accounting | 5 | 16.59 | 3.318 | 0.31797 | ||
| Human Resources | 5 | 15.01 | 3.002 | 0.21947 | ||
| Between Groups | 3.459895 | 3 | 1.153298 | 3.330826 | 0.046214 | 3.238872 |
| Within Groups | 5.54 | 16 | 0.34625 | |||
| Total | 8.999895 | 19 |
So the p -value[latex]=0.0462[/latex].
Because p -value[latex]=0.0462 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that there is a difference in the average GPA of the students in the different programs.
A manufacturing company runs three different production lines to produce one of its products. The company wants to know if the average production rate is the same for the three lines. For each production line, a sample of eight hour shifts was taken and the number of items produced during each shift was recorded in the table below.
| 35 | 21 | 31 |
| 35 | 36 | 34 |
| 36 | 22 | 24 |
| 39 | 38 | 21 |
| 37 | 28 | 27 |
| 36 | 34 | 29 |
| 31 | 35 | 33 |
| 38 | 39 | 20 |
| 33 | 40 | 24 |
Assume the numbers of items produced on each line during an eight hour shift are normally distributed and have equal variance. At the 1% significance level, is there a difference in the average production rate for the three lines?
Let Line 1 be population 1, let Line 2 be population 2, and let Line 3 be population 3.
| Line 1 | 9 | 320 | 35.55556 | 6.027778 | ||
| Line 2 | 9 | 293 | 32.55556 | 51.52778 | ||
| Line 3 | 9 | 243 | 27 | 26 | ||
| Between Groups | 339.1852 | 2 | 169.5926 | 6.089096 | 0.007264 | 5.613591 |
| Within Groups | 668.4444 | 24 | 27.85185 | |||
| Total | 1007.63 | 26 |
So the p -value[latex]=0.0073[/latex].
Because p -value[latex]=0.0073 \lt 0.01=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 1% significance level there is enough evidence to suggest that there is a difference in the average production rate of the three lines.
Concept Review
A one-way ANOVA hypothesis test determines if several population means are equal. In order to conduct a one-way ANOVA test, the following assumptions must be met:
- Each population from which a sample is taken is assumed to be normal.
- All samples are randomly selected and independent.
The analysis of variance procedure compares the variation between groups [latex]MST[/latex] to the variation within groups [latex]MSE[/latex]. The ratio of these two estimates of variance is the [latex]F[/latex]-score from an [latex]F[/latex]-distribution with [latex]df_1=k-1[/latex] and [latex]df_2=n-k[/latex]. The p -value for the test is the area in the right tail of the [latex]F[/latex]-distribution. The statistics used in an ANOVA test are summarized in the ANOVA summary table generated by Excel.
The one-way ANOVA hypothesis test for three or more population means is a well established process:
- Write down the null and alternative hypotheses in terms of the population means. The null hypothesis is the claim that the population means are all equal and the alternative hypothesis is the claim that at least one of the population means is different from the others.
- Collect the sample information for the test and identify the significance level.
- The p -value is the area in the right tail of the [latex]F[/latex]-distribution. Use the ANOVA summary table generated by Excel to find the p -value.
- Compare the p -value to the significance level and state the outcome of the test.
Attribution
“ 13.1 One-Way ANOVA “ and “ 13.2 The F Distribution and the F-Ratio “ in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License .
Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Two-Way ANOVA | Examples & When To Use It
Two-Way ANOVA | Examples & When To Use It
Published on March 20, 2020 by Rebecca Bevans . Revised on June 22, 2023.
ANOVA (Analysis of Variance) is a statistical test used to analyze the difference between the means of more than two groups.
A two-way ANOVA is used to estimate how the mean of a quantitative variable changes according to the levels of two categorical variables. Use a two-way ANOVA when you want to know how two independent variables, in combination, affect a dependent variable.
Table of contents
When to use a two-way anova, how does the anova test work, assumptions of the two-way anova, how to perform a two-way anova, interpreting the results of a two-way anova, how to present the results of a a two-way anova, other interesting articles, frequently asked questions about two-way anova.
You can use a two-way ANOVA when you have collected data on a quantitative dependent variable at multiple levels of two categorical independent variables.
A quantitative variable represents amounts or counts of things. It can be divided to find a group mean.
A categorical variable represents types or categories of things. A level is an individual category within the categorical variable.
You should have enough observations in your data set to be able to find the mean of the quantitative dependent variable at each combination of levels of the independent variables.
Both of your independent variables should be categorical. If one of your independent variables is categorical and one is quantitative, use an ANCOVA instead.
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

ANOVA tests for significance using the F test for statistical significance . The F test is a groupwise comparison test, which means it compares the variance in each group mean to the overall variance in the dependent variable.
If the variance within groups is smaller than the variance between groups, the F test will find a higher F value, and therefore a higher likelihood that the difference observed is real and not due to chance.
A two-way ANOVA with interaction tests three null hypotheses at the same time:
- There is no difference in group means at any level of the first independent variable.
- There is no difference in group means at any level of the second independent variable.
- The effect of one independent variable does not depend on the effect of the other independent variable (a.k.a. no interaction effect).
A two-way ANOVA without interaction (a.k.a. an additive two-way ANOVA) only tests the first two of these hypotheses.
| Null hypothesis (H ) | Alternate hypothesis (H ) |
|---|---|
| There is no difference in average yield for any fertilizer type. | There is a difference in average yield by fertilizer type. |
| There is no difference in average yield at either planting density. | There is a difference in average yield by planting density. |
| The effect of one independent variable on average yield does not depend on the effect of the other independent variable (a.k.a. no interaction effect). | There is an interaction effect between planting density and fertilizer type on average yield. |
To use a two-way ANOVA your data should meet certain assumptions.Two-way ANOVA makes all of the normal assumptions of a parametric test of difference:
- Homogeneity of variance (a.k.a. homoscedasticity )
The variation around the mean for each group being compared should be similar among all groups. If your data don’t meet this assumption, you may be able to use a non-parametric alternative , like the Kruskal-Wallis test.
- Independence of observations
Your independent variables should not be dependent on one another (i.e. one should not cause the other). This is impossible to test with categorical variables – it can only be ensured by good experimental design .
In addition, your dependent variable should represent unique observations – that is, your observations should not be grouped within locations or individuals.
If your data don’t meet this assumption (i.e. if you set up experimental treatments within blocks), you can include a blocking variable and/or use a repeated-measures ANOVA.
- Normally-distributed dependent variable
The values of the dependent variable should follow a bell curve (they should be normally distributed ). If your data don’t meet this assumption, you can try a data transformation.
The dataset from our imaginary crop yield experiment includes observations of:
- Final crop yield (bushels per acre)
- Type of fertilizer used (fertilizer type 1, 2, or 3)
- Planting density (1=low density, 2=high density)
- Block in the field (1, 2, 3, 4).
The two-way ANOVA will test whether the independent variables (fertilizer type and planting density) have an effect on the dependent variable (average crop yield). But there are some other possible sources of variation in the data that we want to take into account.
We applied our experimental treatment in blocks, so we want to know if planting block makes a difference to average crop yield. We also want to check if there is an interaction effect between two independent variables – for example, it’s possible that planting density affects the plants’ ability to take up fertilizer.
Because we have a few different possible relationships between our variables, we will compare three models:
- A two-way ANOVA without any interaction or blocking variable (a.k.a an additive two-way ANOVA).
- A two-way ANOVA with interaction but with no blocking variable.
- A two-way ANOVA with interaction and with the blocking variable.
Model 1 assumes there is no interaction between the two independent variables. Model 2 assumes that there is an interaction between the two independent variables. Model 3 assumes there is an interaction between the variables, and that the blocking variable is an important source of variation in the data.
By running all three versions of the two-way ANOVA with our data and then comparing the models, we can efficiently test which variables, and in which combinations, are important for describing the data, and see whether the planting block matters for average crop yield.
This is not the only way to do your analysis, but it is a good method for efficiently comparing models based on what you think are reasonable combinations of variables.
Running a two-way ANOVA in R
We will run our analysis in R. To try it yourself, download the sample dataset.
Sample dataset for a two-way ANOVA
After loading the data into the R environment, we will create each of the three models using the aov() command, and then compare them using the aictab() command. For a full walkthrough, see our guide to ANOVA in R .
This first model does not predict any interaction between the independent variables, so we put them together with a ‘+’.
In the second model, to test whether the interaction of fertilizer type and planting density influences the final yield, use a ‘ * ‘ to specify that you also want to know the interaction effect.
Because our crop treatments were randomized within blocks, we add this variable as a blocking factor in the third model. We can then compare our two-way ANOVAs with and without the blocking variable to see whether the planting location matters.
Model comparison
Now we can find out which model is the best fit for our data using AIC ( Akaike information criterion ) model selection.
AIC calculates the best-fit model by finding the model that explains the largest amount of variation in the response variable while using the fewest parameters. We can perform a model comparison in R using the aictab() function.
The output looks like this:
The AIC model with the best fit will be listed first, with the second-best listed next, and so on. This comparison reveals that the two-way ANOVA without any interaction or blocking effects is the best fit for the data.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
You can view the summary of the two-way model in R using the summary() command. We will take a look at the results of the first model, which we found was the best fit for our data.
The model summary first lists the independent variables being tested (‘fertilizer’ and ‘density’). Next is the residual variance (‘Residuals’), which is the variation in the dependent variable that isn’t explained by the independent variables.
The following columns provide all of the information needed to interpret the model:
- Df shows the degrees of freedom for each variable (number of levels in the variable minus 1).
- Sum sq is the sum of squares (a.k.a. the variation between the group means created by the levels of the independent variable and the overall mean).
- Mean sq shows the mean sum of squares (the sum of squares divided by the degrees of freedom).
- F value is the test statistic from the F test (the mean square of the variable divided by the mean square of each parameter).
- Pr(>F) is the p value of the F statistic, and shows how likely it is that the F value calculated from the F test would have occurred if the null hypothesis of no difference was true.
From this output we can see that both fertilizer type and planting density explain a significant amount of variation in average crop yield ( p values < 0.001).
Post-hoc testing
ANOVA will tell you which parameters are significant, but not which levels are actually different from one another. To test this we can use a post-hoc test. The Tukey’s Honestly-Significant-Difference (TukeyHSD) test lets us see which groups are different from one another.

This output shows the pairwise differences between the three types of fertilizer ($fertilizer) and between the two levels of planting density ($density), with the average difference (‘diff’), the lower and upper bounds of the 95% confidence interval (‘lwr’ and ‘upr’) and the p value of the difference (‘p-adj’).
From the post-hoc test results, we see that there are significant differences ( p < 0.05) between:
- fertilizer groups 3 and 1,
- fertilizer types 3 and 2,
- the two levels of planting density,
but no difference between fertilizer groups 2 and 1.
Once you have your model output, you can report the results in the results section of your thesis , dissertation or research paper .
When reporting the results you should include the F statistic, degrees of freedom, and p value from your model output.
You can discuss what these findings mean in the discussion section of your paper.
You may also want to make a graph of your results to illustrate your findings.
Your graph should include the groupwise comparisons tested in the ANOVA, with the raw data points, summary statistics (represented here as means and standard error bars), and letters or significance values above the groups to show which groups are significantly different from the others.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Chi square test of independence
- Statistical power
- Descriptive statistics
- Degrees of freedom
- Pearson correlation
- Null hypothesis
Methodology
- Double-blind study
- Case-control study
- Research ethics
- Data collection
- Hypothesis testing
- Structured interviews
Research bias
- Hawthorne effect
- Unconscious bias
- Recall bias
- Halo effect
- Self-serving bias
- Information bias
The only difference between one-way and two-way ANOVA is the number of independent variables . A one-way ANOVA has one independent variable, while a two-way ANOVA has two.
- One-way ANOVA : Testing the relationship between shoe brand (Nike, Adidas, Saucony, Hoka) and race finish times in a marathon.
- Two-way ANOVA : Testing the relationship between shoe brand (Nike, Adidas, Saucony, Hoka), runner age group (junior, senior, master’s), and race finishing times in a marathon.
All ANOVAs are designed to test for differences among three or more groups. If you are only testing for a difference between two groups, use a t-test instead.
In ANOVA, the null hypothesis is that there is no difference among group means. If any group differs significantly from the overall group mean, then the ANOVA will report a statistically significant result.
Significant differences among group means are calculated using the F statistic, which is the ratio of the mean sum of squares (the variance explained by the independent variable) to the mean square error (the variance left over).
If the F statistic is higher than the critical value (the value of F that corresponds with your alpha value, usually 0.05), then the difference among groups is deemed statistically significant.
A factorial ANOVA is any ANOVA that uses more than one categorical independent variable . A two-way ANOVA is a type of factorial ANOVA.
Some examples of factorial ANOVAs include:
- Testing the combined effects of vaccination (vaccinated or not vaccinated) and health status (healthy or pre-existing condition) on the rate of flu infection in a population.
- Testing the effects of marital status (married, single, divorced, widowed), job status (employed, self-employed, unemployed, retired), and family history (no family history, some family history) on the incidence of depression in a population.
- Testing the effects of feed type (type A, B, or C) and barn crowding (not crowded, somewhat crowded, very crowded) on the final weight of chickens in a commercial farming operation.
Quantitative variables are any variables where the data represent amounts (e.g. height, weight, or age).
Categorical variables are any variables where the data represent groups. This includes rankings (e.g. finishing places in a race), classifications (e.g. brands of cereal), and binary outcomes (e.g. coin flips).
You need to know what type of variables you are working with to choose the right statistical test for your data and interpret your results .
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Two-Way ANOVA | Examples & When To Use It. Scribbr. Retrieved July 8, 2024, from https://www.scribbr.com/statistics/two-way-anova/
Is this article helpful?
Rebecca Bevans
Other students also liked, anova in r | a complete step-by-step guide with examples, one-way anova | when and how to use it (with examples), what is your plagiarism score.
- Search Search Please fill out this field.
Using ANOVA
What anova reveals, one-way vs. two-way anova, anova example, the bottom line.
- Fundamental Analysis
What Is Analysis of Variance (ANOVA)?
How To Use This Statistical Analysis Tool
:max_bytes(150000):strip_icc():format(webp)/wk_headshot_aug_2018_02__william_kenton-5bfc261446e0fb005118afc9.jpg)
Erika Rasure is globally-recognized as a leading consumer economics subject matter expert, researcher, and educator. She is a financial therapist and transformational coach, with a special interest in helping women learn how to invest.
:max_bytes(150000):strip_icc():format(webp)/CSP_ER9-ErikaR.-dce5c7e19ef04426804e6b611fb1b1b4.jpg)
Analysis of variance (ANOVA) is a statistical test used to assess the difference between the means of more than two groups. At its core, ANOVA allows you to simultaneously compare arithmetic means across groups. You can determine whether the differences observed are due to random chance or if they reflect genuine, meaningful differences.
A one-way ANOVA uses one independent variable. A two-way ANOVA uses two independent variables. Analysts use the ANOVA test to determine the influence of independent variables on the dependent variable in a regression study. While this can sound arcane to those new to statistics, the applications of ANOVA are as diverse as they are profound. From medical researchers investigating the efficacy of new treatments to marketers analyzing consumer preferences, ANOVA has become an indispensable tool for understanding complex systems and making data-driven decisions.
Key Takeaways
- ANOVA is a statistical method that simultaneously compares means across several groups to determine if observed differences are due to chance or reflect genuine distinctions.
- A one-way ANOVA uses one independent variable. A two-way ANOVA uses two independent variables.
- By partitioning total variance into components, ANOVA unravels relationships between variables and identifies true sources of variation.
- ANOVA can handle multiple factors and their interactions, providing a robust way to better understand intricate relationships.
Xiaojie Liu / Investopedia
An ANOVA test can be applied when data needs to be experimental. Analysis of variance is employed if there is no access to statistical software, and ANOVA must be calculated by hand. It's simple to use and best suited for small samples involving subjects, test groups, and between and among groups.
ANOVA is like several two-sample t-tests . However, it results in fewer type I errors . ANOVA groups differences by comparing each group's means and includes spreading the variance into diverse sources. Analysts use a one-way ANOVA with collected data about one independent variable and one dependent variable. A two-way ANOVA uses two independent variables. The independent variable should have at least three different groups or categories. ANOVA determines if the dependent variable changes according to the level of the independent variable.
Researchers might test students from several colleges to see if students from one of them consistently outperforms students from the other schools. In a business application, a research and development researcher might test two ways of creating a product to see if one is better than the other in cost efficiency.
ANOVA's versatility and ability to handle multiple variables make it a valuable tool for researchers and analysts across various fields. By comparing means and partitioning variance, ANOVA provides a robust way to understand the relationships between variables and identify significant differences among groups.
ANOVA Formula
F = MST MSE where: F = ANOVA coefficient MST = Mean sum of squares due to treatment MSE = Mean sum of squares due to error \begin{aligned} &\text{F} = \frac{ \text{MST} }{ \text{MSE} } \\ &\textbf{where:} \\ &\text{F} = \text{ANOVA coefficient} \\ &\text{MST} = \text{Mean sum of squares due to treatment} \\ &\text{MSE} = \text{Mean sum of squares due to error} \\ \end{aligned} F = MSE MST where: F = ANOVA coefficient MST = Mean sum of squares due to treatment MSE = Mean sum of squares due to error
History of ANOVA
The t- and z-test methods developed in the 20th century were used for statistical analysis. In 1918, when Ronald Fisher created the analysis of variance method. For this reason, ANOVA is also called the Fisher analysis of variance, and it's an extension of the t- and z-tests. The term became well-known in 1925 after appearing in Fisher's book, "Statistical Methods for Research Workers." It was first employed in experimental psychology and later expanded to other subjects.
The ANOVA test is the first step in analyzing factors that affect a given data set. Once the test is finished, an analyst performs further testing on the factors that measurably might be contributing to the data's inconsistency. The analyst utilizes the ANOVA test results in an F-test to generate further data that aligns with the proposed regression models.
If you need reminders on these terms, here's a cheat sheet for many of the major statistical tests found in finance studies:
| Cheat Sheet on Common Statistical Tests in Finance and Investing | |||
|---|---|---|---|
| Compare the arithmetical means of two or more groups while controlling for the effects of a continuous variable | • Normal distribution • Comparing multiple independent variables with a covariate | • Analyzing investment returns while controlling for market volatility • Evaluating the effectiveness of financial strategies while accounting for economic conditions | |
| Compare the means of three or more groups | • Data is normally distributed | • Comparing financial performance across different sectors or investment strategies | |
| Test for association between two categorical variables (can't be measured on a numerical scale) | • Data is categorical (e.g., investment choices, market segments) | • Analyzing customer demographics and portfolio allocations | |
| Measure the strength and direction of a linear relationship between two variables | • Data is continuous | • Assessing risk and return of assets, portfolio diversification | |
| Checks if errors in a prediction model are related over time | • Time series data | • Detecting serial correlation in stock prices, market trends | |
| Compare variances of two or more groups | • Data is normally distributed | • Testing the equality of variances in stock returns and portfolio performance | |
| Test for a causal relationship between two time series | • Time series data | • Determining if one economic indicator predicts another | |
| Test for normality of data | • Continuous data | • Assessing if financial data follows a normal distribution | |
| Compare medians of two independent samples | • Data is not normally distributed | • Comparing the financial performance of two groups with non-normal distributions | |
| Compare means of two or more groups on multiple dependent variables simultaneously | • Data is normally distributed • Analyzing multiple related outcome variables | • Assessing the impact of different investment portfolios on multiple financial metrics • Evaluating the overall financial health of companies based on various performance indicators | |
| Compare a sample mean to a known population mean | • Data is normally distributed or the sample size is large | • Comparing actual vs. expected returns | |
| Compare means of two related samples (e.g., before and after measurements) | • Data is normally distributed or the sample size is large | • Evaluating if a financial change has been effective | |
| Predict the value of one variable based on the value of another variable | • Data is continuous | • Modeling stock prices • Predicting future returns | |
| Test for differences in medians between two related samples | • Data is not normally distributed | • Non-parametric alternative to paired t-test in financial studies | |
| Compare the means of two groups | • Data is normally distributed or the sample size is large | • Comparing the performance of two investment strategies | |
| Compare medians of two independent samples | • Data is not normally distributed | • Non-parametric alternative to independent t-test in finance | |
| Compare a sample mean to a known population mean | • Data is normally distributed and population standard deviation is known | • Testing hypotheses about market averages | |
ANOVA splits an observed aggregate variability inside a data set into two parts: systematic factors and random factors. The systematic factors influence the given data set, while the random factors do not.
The ANOVA test lets you compare more than two groups simultaneously to determine whether a relationship exists between them. The result of the ANOVA formula, the F statistic or F-ratio, allows you to analyze several data groups to assess the variability between samples and within samples.
If no real difference exists between the tested groups, called the null hypothesis , the result of the ANOVA's F-ratio statistic will be close to one. The distribution of all possible values of the F statistic is the F-distribution. This is a group of distribution functions with two characteristic numbers, called the numerator degrees of freedom and the denominator degrees of freedom.
Uses one independent variable or factor
Assesses the impact of a single categorical variable on a continuous dependent variable, identifying significant differences among group means
Does not account for interactions
Uses two independent variables or factors
Used to not only understand the individual effects of two different factors but also how the combination of these two factors influences the outcome
Can test for interactions between factors
A one-way ANOVA evaluates the impact of a single factor on a sole response variable. It determines whether all the samples are the same. The one-way ANOVA is used to determine whether there are any statistically significant differences between the means of three or more independent groups.
A two-way ANOVA is an extension of the one-way ANOVA. With a one-way, there is one independent variable affecting a dependent variable. With a two-way ANOVA, there are two independent variables. For example, a two-way ANOVA allows a company to compare worker productivity based on two independent variables, such as salary and skill set. It's utilized to see the interaction between the two factors and test the effect of two factors simultaneously.
Suppose you want to assess the performance of different investment portfolios across various market conditions. The goal is to determine which portfolio strategy performs best under what conditions.
You have three portfolio strategies:
- Technology portfolio (tech stocks): High-risk, high return
- Balanced portfolio (stocks and bonds): Moderate-risk, moderate return
- Fixed-income portfolio (bonds and money market instruments): Low-risk, low return
You also want to check against two market conditions:
- A bull market
- A bear market
A one-way ANOVA could give a broad overview of portfolio strategy performance, while a two-way ANOVA adds a deeper understanding by including the varying market conditions.
One-Way ANOVA
A one-way ANOVA could be used to initially analyze the performance differences among the three different portfolios without considering the impact of market conditions. The independent variable would be the type of investment portfolio, and the dependent variable would be the returns generated.
You would group the returns of the technology, balanced, and fixed-income portfolios for a preset period and compare the mean returns of the three portfolios to determine if there are statistically significant differences. This would help determine whether different investment strategies result in different returns, but it would not account for how different market conditions might influence these returns.
Two-Way ANOVA
Meanwhile, a two-way ANOVA would be more appropriate for analyzing both the effects of the investment portfolio and the market conditions, as well as any interaction between these two factors on the returns.
MANOVA (multivariate ANOVA), differs from ANOVA as it tests for several dependent variables simultaneously while the ANOVA assesses only one dependent variable at a time.
You would first need to group each portfolio's returns under both bull and bear market conditions. Next, you would compare the mean returns across both factors to determine the effect of the investment strategy on returns, the effect of market conditions on returns, and whether the effectiveness of a particular investment strategy depends on the market condition.
Suppose the technology portfolio performs significantly better in bull markets but underperforms in bear markets, while the fixed-income portfolio provides stable returns regardless of the market. Looking at these interactions could help you see when it's best to advise using a technology portfolio and when a bear market means it's soundest to turn to a fixed-income portfolio.
How Does ANOVA Differ From a T-Test?
ANOVA differs from t-tests in that ANOVA can compare three or more groups while t-tests are only useful for comparing two groups at one time.
What Is Analysis of Covariance (ANCOVA)?
Analysis of covariance combines ANOVA and regression. It can be useful for understanding within-group variance that ANOVA tests do not explain.
Does ANOVA Rely on Any Assumptions?
Yes, ANOVA tests assume that the data is normally distributed and that variance levels in each group are roughly equal. Finally, it assumes that all observations are made independently. If these assumptions are inaccurate, ANOVA may not be useful for comparing groups.
ANOVA is a robust statistical tool that allows researchers and analysts to simultaneously compare arithmetical means across multiple groups. By dividing variance into different sources, ANOVA helps identify significant differences and uncover meaningful relationships between variables. Its versatility and ability to handle various factors make it an essential tool for many fields that use statistics, including finance and investing.
Understanding ANOVA's principles, forms, and applications is crucial for leveraging this technique effectively. Whether using a one-way or two-way ANOVA, researchers can gain greater clarity about complex systems to make data-driven decisions. As with any statistical method, it's essential to interpret the results carefully and consider the context and limitations of the analysis.
Genetic Epidemiology, Translational Neurogenomics, Psychiatric Genetics and Statistical Genetics-QIMR Berghofer Medical Research Institute. " The Correlation Between Relatives on the Supposition of Mendelian Inheritance ."
Ronald Fisher. " Statistical Methods for Research Workers ." Springer-Verlag New York, 1992.
:max_bytes(150000):strip_icc():format(webp)/investing3-5bfc2b8e46e0fb0026016f32.jpg)
- Terms of Service
- Editorial Policy
- Privacy Policy

IMAGES
VIDEO
COMMENTS
The hypothesis is based on available information and the investigator's belief about the population parameters. The specific test considered here is called analysis of variance (ANOVA) and is a test of hypothesis that is appropriate to compare means of a continuous variable in two or more independent comparison groups.
Learn how to use one-way ANOVA to test the difference between the means of more than two groups with one independent variable. Find out the assumptions, steps, and interpretations of this statistical test with R code and examples.
The ANOVA Test. An ANOVA test is a way to find out if survey or experiment results are significant. In other words, they help you to figure out if you need to reject the null hypothesis or accept the alternate hypothesis. Basically, you're testing groups to see if there's a difference between them.
One-Way ANOVA: The Process. A one-way ANOVA uses the following null and alternative hypotheses: H0 (null hypothesis): μ1 = μ2 = μ3 = … = μk (all the population means are equal) H1 (alternative hypothesis): at least one population mean is different from the rest. You will typically use some statistical software (such as R, Excel, Stata ...
ANOVA 1: Calculating SST (total sum of squares) ANOVA 2: Calculating SSW and SSB (total sum of squares within and between) ANOVA 3: Hypothesis test with F-statistic. Analysis of variance, or ANOVA, is an approach to comparing data with multiple means across different groups, and allows us to see patterns and trends within complex and varied ...
Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures (such as the "variation" among and between groups) used to analyze the differences among means. ANOVA was developed by the statistician Ronald Fisher.ANOVA is based on the law of total variance, where the observed variance in a particular variable is partitioned into components ...
Learn how to use ANOVA (Analysis of Variance) to test differences between two or more means. Find out the key terms, formulas, types, and examples of ANOVA for various research designs.
ANOVA tests the non-specific null hypothesis that all four population means are equal. That is, \[\mu _{false} = \mu _{felt} = \mu _{miserable} = \mu _{neutral}\] This non-specific null hypothesis is sometimes called the omnibus null hypothesis. When the omnibus null hypothesis is rejected, the conclusion is that at least one population mean is ...
Step 7: Based on steps 5 and 6, draw a conclusion about H0. If the F\calculated F \calculated from the data is larger than the Fα F α, then you are in the rejection region and you can reject the null hypothesis with (1 − α) ( 1 − α) level of confidence. Note that modern statistical software condenses steps 6 and 7 by providing a p p -value.
Use one way ANOVA to compare the means of three or more groups. This analysis is an inferential hypothesis test that uses samples to draw conclusions about populations. Specifically, it tells you whether your sample provides sufficient evidence to conclude that the groups' population means are different. ANOVA stands for analysis of variance.
ANOVA stands for Analysis of Variance. It's a statistical method to analyze differences among group means in a sample. ANOVA tests the hypothesis that the means of two or more populations are equal, generalizing the t-test to more than two groups. It's commonly used in experiments where various factors' effects are compared.
ANOVA, short for Analysis of Variance, is a statistical method used to see if there are significant differences between the averages of three or more unrelated groups. This technique is especially useful when comparing more than two groups, which is a limitation of other tests like the t-test and z-test. For example, ANOVA can compare average ...
We test the null hypothesis of equal means of the response in every group versus the alternative hypothesis of one or more group means being different from the others. A one-way ANOVA hypothesis test determines if several population means are equal. The distribution for the test is the F distribution with two different degrees of freedom ...
The ANOVA tests the null hypothesis, which states that samples in all groups are drawn from populations with the same mean values. To do this, two estimates are made of the population variance. These estimates rely on various assumptions . The ANOVA produces an F-statistic, the ratio of the variance calculated among the means to the variance ...
The three-way ANOVA test is also referred to as a three-factor ANOVA test. Calculating ANOVA: For ANOVA tests, we would set up a null and alternative hypothesis like so: Hnull → µ1 = µ2 = µ3 ...
The sample data are organized as follows: The hypotheses of interest in an ANOVA are as follows: H 1: Means are not all equal. where k = the number of independent comparison groups. In this example, the hypotheses are: H 1: The means are not all equal. The null hypothesis in ANOVA is always that there is no difference in means.
Dr C. 8 years ago. ANOVA is inherently a 2-sided test. Say you have two groups, A and B, and you want to run a 2-sample t-test on them, with the alternative hypothesis being: Ha: µ.a ≠ µ.b. You will get some test statistic, call it t, and some p-value, call it p1. If you then run an ANOVA on these two groups, you will get an test statistic ...
The following examples show how to decide to reject or fail to reject the null hypothesis in both a one-way ANOVA and two-way ANOVA. Example 1: One-Way ANOVA. Suppose we want to know whether or not three different exam prep programs lead to different mean scores on a certain exam. To test this, we recruit 30 students to participate in a study ...
These statements are called Hypothesis. A hypothesis is an educated guess about something in the world around us. It should be testable either by experiment or observation. Just like any other kind of hypothesis that you might have studied in statistics, ANOVA also uses a Null hypothesis and an Alternate hypothesis.
A one-way ANOVA hypothesis test determines if several population means are equal. In order to conduct a one-way ANOVA test, the following assumptions must be met: Each population from which a sample is taken is assumed to be normal. All samples are randomly selected and independent. The populations are assumed to have equal variances.
The intent of hypothesis testing is formally examine two opposing conjectures (hypotheses), H0 and HA. These two hypotheses are mutually exclusive and exhaustive so that one is true to the exclusion of the other. We accumulate evidence - collect and analyze sample information - for the purpose of determining which of the two hypotheses is true ...
ANOVA (Analysis of Variance) is a statistical test used to analyze the difference between the means of more than two groups. A two-way ANOVA is used to estimate how the mean of a quantitative variable changes according to the levels of two categorical variables. Use a two-way ANOVA when you want to know how two independent variables, in ...
Analysis Of Variance - ANOVA: Analysis of variance (ANOVA) is an analysis tool used in statistics that splits the aggregate variability found inside a data set into two parts: systematic factors ...