z score null hypothesis calculator

Hypothesis Testing Calculator

Type ii error.

The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.

Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.

To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.

In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.

To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.

When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.

Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.

Z-Test Calculator

This Z-test calculator computes data for both one-sample and two-sample Z-tests. It also provides a diagram to show the position of the Z-score and the acceptance/rejection regions. When making a two-sample Z-test calculation, the population mean difference, d, represents the difference between the population means of sample one and sample two, which is μ 1 -μ 2 . To use this calculator, simply select the type of calculation from the tab, enter the values, and click the 'Calculate' button.

The Z-test is a statistical procedure used to determine whether there is a significant difference between means, either between a sample mean and a known population mean (one-sample Z-test) or between the means of two independent samples (two-sample Z-test). It assumes that the data is normally distributed and is particularly useful when the sample sizes are large (>30) and the population standard deviations are known. When analyzing data to make informed decisions, statistical hypothesis tests are indispensable tools used to determine if evidence exists to reject a prevailing assumption or theory, known as the null hypothesis. The Z-test is one of these tests.

One-Sample Z-Test

The one-sample Z-test is used when you want to compare the mean of a single sample to a known population mean to see if there is a significant difference. This is particularly common in quality control and other scenarios where the standard deviation of the population is known.

• Null Hypothesis (H 0 ): The sample mean is equal to the population mean (x̅=μ).
• Alternative Hypothesis (H 1 ): The sample mean is not equal to the population mean (x̅≠μ). This can also be one-tailed (x̅>μ or x̅<μ) depending on the direction of interest.

The formula for the Z-statistic in a one-sample Z-test is:

• x̅ is the sample mean
• μ is the population mean
• σ is the population standard deviation
• n is the sample size

Example: Suppose a school administrator knows the national average score for a standardized test is 500 with a standard deviation of 50. A sample of 100 students from a new teaching program scores an average of 520. To determine if this program significantly differs from the national average:

This Z-value would then be compared against a critical value from the Z-distribution table typically at a 0.05 significance level. The critical value for a 0.05 significance level is approximately ±1.96. The Z-value of 4 is greater than 1.96. Therefore, the null hypothesis is rejected and the score of this program is considered significantly different from the national average at the 0.05 significance level.

Two-Sample Z-Test

The two-sample Z-test (or independent samples Z-test) compares the means from two independent groups to determine if there is a statistically significant difference between them.

• Null Hypothesis (H 0 ): The two population means have a difference of d (μ 1 -μ 2 =d). If d is 0, the null hypothesis states that the two population means are equal (μ 1 =μ 2 ).
• Alternative Hypothesis (H 1 ): The difference between two population means is not d (μ 1 -μ 2 ≠d), which can also be directional (μ 1 -μ 2 >d or μ 1 -μ 2 <d). If d is 0, the alternative hypothesis becomes μ 1 ≠μ 2 , or μ 1 >μ 2 or μ 1 <μ 2 if it is directional.

The formula for calculating the Z-statistic in a two-sample Z-test is:

• x̅ 1 and x̅ 2 are the sample means of groups 1 and 2, respectively
• μ 1 and μ 2 are the population means, with μ 1 - μ 2 = d. d is often hypothesized to be zero under the null hypothesis.
• σ 1 and σ 2 are the population standard deviations
• n 1 and n 2 are the sample sizes of the two groups

Example: Consider two groups of employees from different branches of a company undergoing training. Group A has 50 employees with an average score of 80 and a standard deviation of 10, and Group B has 50 employees with an average score of 75 and a standard deviation of 12. To test if there's a significant difference:

This Z-value is then compared to the critical Z-values to assess significance. The critical value of a 0.05 significance level is around ±1.95. The Z-value of 2.26 is more than 1.95. Therefore, the two group has significant difference at 0.05 significance level.

Significance Level

The significance level (α) is a critical concept in hypothesis testing. It represents the probability threshold below which the null hypothesis will be rejected. Common levels are 0.05 (5%) or 0.01 (1%). The choice of α affects the Z-critical value, which is used to determine whether to reject the null hypothesis based on the computed Z-score.

• Critical Value: This is a point on the Z-distribution that the test statistic must exceed to reject the null hypothesis. For instance, at a 5% significance level in a two-tailed test, the critical values are approximately ±1.96. The significance level (probability) and critical value (Z-score) can be converted with each other the Z-distribution table or use our Z/P converter .

Using the above examples, if the computed Z-scores exceed the respective critical values, the null hypotheses in each case would be rejected, indicating a statistically significant difference as per the alternative hypotheses. These examples demonstrate how the Z-test is applied in different scenarios to test hypotheses concerning population means.

Z-score Calculator

Use this calculator to compute the z-score of a normal distribution.

Z-score and Probability Converter

Please provide any one value to convert between z-score and probability. This is the equivalent of referencing a z-table.

Probability between Two Z-scores

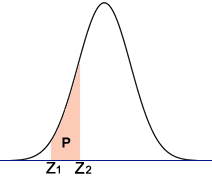
Use this calculator to find the probability (area P in the diagram) between two z-scores.

Related Standard Deviation Calculator

What is z-score?

The z-score, also referred to as standard score, z-value, and normal score, among other things, is a dimensionless quantity that is used to indicate the signed, fractional, number of standard deviations by which an event is above the mean value being measured. Values above the mean have positive z-scores, while values below the mean have negative z-scores.

The z-score can be calculated by subtracting the population mean from the raw score, or data point in question (a test score, height, age, etc.), then dividing the difference by the population standard deviation:

where x is the raw score, μ is the population mean, and σ is the population standard deviation. For a sample, the formula is similar, except that the sample mean and population standard deviation are used instead of the population mean and population standard deviation.

The z-score has numerous applications and can be used to perform a z-test, calculate prediction intervals, process control applications, comparison of scores on different scales, and more.

A z-table, also known as a standard normal table or unit normal table, is a table that consists of standardized values that are used to determine the probability that a given statistic is below, above, or between the standard normal distribution. A z-score of 0 indicates that the given point is identical to the mean. On the graph of the standard normal distribution, z = 0 is therefore the center of the curve. A positive z-value indicates that the point lies to the right of the mean, and a negative z-value indicates that the point lies left of the mean. There are a few different types of z-tables.

The values in the table below represent the area between z = 0 and the given z-score.

How to read the z-table

In the table above,

• the column headings define the z-score to the hundredth's place.
• the row headings define the z-score to the tenth's place.
• each value in the table is the area between z = 0 and the z-score of the given value, which represents the probability that a data point will lie within the referenced region in the standard normal distribution.

For example, referencing the right-tail z-table above, a data point with a z-score of 1.12 corresponds to an area of 0.36864 (row 13, column 4). This means that for a normally distributed population, there is a 36.864% chance, a data point will have a z-score between 0 and 1.12.

Because there are various z-tables, it is important to pay attention to the given z-table to know what area is being referenced.

One Sample Z-Test Calculator

Enter sample data, z test online, assumptions, required sample data.

One sample z test calculator

Welcome to our One Sample Z Test Calculator! This tool helps you perform a one-sample Z test for hypothesis testing quickly and accurately. our calculator simplifies the process of determining p-values, critical value, test statistics, decision and Conclusion.

Table of Contents

Understanding the one sample z test.

• Related Calculators

How to Use the One Sample Z Test Calculator

Applications of the one sample z test, assumption for one sample z test :, frequently asked questions (faqs).

The one-sample Z test is used to assess whether there is a significant difference between the sample mean and the population mean. This test is appropriate when the population standard deviation is known and the sample size is large enough \( \mathrm{( n > 30)}\).

To determine if a population's mean is greater than, less than, or equal to a given value, use the one-sample z-test. This test is frequently referred to as the one-sample z-test since the critical values are determined using the standard normal distribution. The population standard deviation must be known in order to use the z-test.

Related Calculators :

Below are more calculators which use the critical value to perform statistical analysis.

• Select Data Type: Choose whether to input summary statistics directly or provide a data set.
• Input Your Data: Enter the necessary values such as the population mean, sample size, sample mean, and population standard deviation.
• Set Hypotheses: Specify the null and alternative hypotheses.
• Calculate: Click the "Calculate" button to see the test statistic, p-value, and other relevant results.

Example of one sample z test hypothesis

First lets find the given parameters

Sample size, \(n =20\), Sample mean, \(\bar x = 42\), Population standard deviation, \(\sigma = 6\), Population mean, \(\mu = 38\), Significance level, \(\alpha = 0.01\)

The null and alternative hypothesis is

\(H_0: \mu = 38\) and \( H_a: \mu > 38 \)

The null hypothesis contains the equality sign and the alternative hypothesis contains the inequality sign.

Now, lets find the Test statistic which is required for find the p-value

Formula for the test statistic is

\( z = \frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}} \)

Put the given values in above formula, we get

\(\frac{42-38}{\frac{6}{\sqrt{20}}} = 2.98 \)

The test statistic is 2.98

Here we round test statistic to two decimal places because this decimal places is used in p-value table to find the test statistic

Next, find the p-value to find the statistical decision

The p-value with test statistic, z = 2.98 is

P( z > 2.98) = 0.0014

The p-value is 0.0014

The p-value in statistical hypothesis testing is the probability of obtaining results at least as extreme as the observed results of a statistical test, assuming that the null hypothesis is true.

The following Excel formula can be used to find the p-value:

=1-NORM.S.DIST(2.98,TRUE)

In this formula 2.98 is represents the test statistic.

Decision : Since the p-value is less than the chosen significance level, the decision is reject the null hypothesis.

Conclusion : There is sufficient evidence to conclude that population mean is greater than 38.

Since the decision is reject the null hypothesis, there is sufficient evidence to support alternative hypothesis.

Interpreting the Results

The results of the one-sample Z test will indicate whether you should reject the null hypothesis. A p-value smaller than α rejects the null hypothesis, showing a substantial difference between the sample and population means.

This test is widely used in various fields including:

• Education: Assessing whether the average test scores of a class differ from the national average.
• Healthcare: Comparing the mean blood pressure level of a group of patients to a known population mean.
• Business: Evaluating if the average sales of a product differ from the company's historical sales data.

The assumption for one sample z test are as follows

1. Continuous Data: It's true that continuous data is necessary. This indicates that rather than being discrete or categorical, the data points are measured on a continuous scale.

2. Simple Random Sample: According to this premise, there is no bias in the sample selection process and every individual in the population has an equal probability of being chosen. By doing this, the sample's representativeness to the population is increased.

3. Normality of Data: It is assumed that the data for a one-sample z-test have a normal distribution. This presumption is essential since the validity of the z-test depends on the characteristics of the normal distribution.

4. Known Population Standard Deviation: The z-test operates under the assumption that the population standard deviation (σ) is known, in contrast to the t-test, which necessitates the sample standard deviation.

What is a one-sample Z test?

A one-sample Z test is a statistical test used to determine whether there is a significant difference between the mean of a sample and a known population mean.

When should I use a one-sample Z test?

You should use this test when the population standard deviation is known and the sample size is large (typically n > 30).

How do I interpret the p-value in a Z test?

The p-value indicates the probability of observing the test results under the null hypothesis. A low p-value (less than the significance level, α) suggests that you should reject the null hypothesis.

Why use our one-sample Z test calculator?

Our calculator offers several advantages:

• Accuracy: Provides precise calculations for your hypothesis testing needs.
• User-Friendly Interface: Easy to navigate and input your data.
• Educational Value: Offers detailed explanations and step-by-step guides to help you understand the results.
• Time-Saving: Quickly computes results, allowing you to focus on analysis and interpretation.
• Versatility: Suitable for various fields such as education, healthcare, and business, making it a valuable tool for a wide range of users.

Z Score Calculator

Use this Z table calculator to easily calculate the Z-score from a given raw score. Also computes areas under the normal curve ( p -values) cut off by a given score. A table of Z scores and corresponding p-values is included, as well as the z score formula. Also calculates Z from p.

Related calculators

• Using the Z score calculator
• What is a Z Distribution?
• What is a "Z score"?
• Z score formula
• Example calculations

    Using the Z score calculator

The z score calculator can be used to derive a z statistic from a raw score and known or estimated distribution mean and standard deviation . If the variance is known instead, then the standard deviation is simply its square root. The output also contains probabilities calculated for different areas under the standard normal curve which correspond to a one-tailed or two-tailed test of significance. The cumulative probabilities are calculated using the standard normal cumulative distribution function (CDF) .

The z statistic calculator can also be used in inverse - to obtain a Z critical value corresponding to a given probability. Simply select "Z score from P" and enter the p-value threshold in the field to obtain the standard score defining the critical region.

    What is a Z Distribution?

The Z distribution is simply the standard normal distribution of the random variable Z meaning it is a normal distribution with mean 0 and variance and standard deviation equal to 1 [1,2,3] . The Z distribution with key quantiles is shown on the graph below:

The fact that the distribution is standardized means that the quantiles are known, and that area between any two Z scores is also known. For example, 68.27% of values would fall between -1 and 1 standard deviations of a Z distribution. Similarly, just over 95% of its probability density falls between -2 and +2 standard deviations. The entire distribution density sums to 1 and just like other normal distributions it is fully defined by its first two moments. These and other qualities make it a useful tool in statistics and probability calculation of various sorts.

Our z score calculator uses the CDF of the Z distribution to find the area under the standard normal curve above, below, between, or outside regions defined by given scores. It uses the inverse CDF to calculate Z scores from p-values.

    What is a "Z score"?

The z-score, also referred to as standard score and z-value is a signed real valued dimensionless quantity which indicates the number of standard deviations by which a given observed data point is distanced from the mean or expected value of a distribution. Standard refers to the fact that they are computed against the standard normal distribution (a.k.a. Z distribution) which is fully defined by its mean and standard deviation of zero and one, respectively.

Z values have numerous applications in statistical inference and estimation. Most commonly they are used in a Z-test of significance as well as confidence interval calculations [4] . They are also used in process control and quality assurance applications (e.g. six sigma ). Due to Z values being standardized scores they are useful in comparing measurements across different scales which is often needed in both scientific and applied disciplines.

    Z score formula

The formula for calculating a z score from a raw score from is given by the simple equation:

Using the above formula one can easily convert a raw score from a normal distribution with known or estimated mean and standard deviation to a standard score. An online Z calculator can perform the arithmetic for you quickly and easily.

    Z table

A Z table contains tabulated values of the Z distribution and their corresponding quantiles, or percentages. Since a table of Z scores can be used to judge either a point null hypothesis (e.g. the effect is exactly zero), as well as the more commonly needed composite nulls such as μ 1 ≤ 0, a proper Z table should contain both types of cumulative probabilities. In the table below, a one-tailed p-value / percentile refers to the area under the standard normal curve to the right of the Z score ( P(X > z) ), whereas a two-tailed p-value / percentile refers to the cumulative probability contained in the union of the areas to the right of -Z and to the left of Z ( P(X < -|z| ∪ X > |z|) ).

Table of commonly used Z-score cut-offs for defining critical regions for normally distributed random variables:

Note that since the standard normal distribution is symmetrical, a two-tailed p-value is exactly twice that of a one-tailed one for the same value of Z. Obviously, such a table has limited utility nowadays when it is much easier to use a free online z table calculator like ours. Refer to the documentation and graphs in our critical value calculator page for more on critical values and regions.

    Example calculations

It is easy to find the Z score corresponding to a given raw score, given that one knows the mean and standard deviation of the normal distribution to which the raw score belongs. Using the z statistic formula above we can easily compute that a raw score from a standard normal distribution is equivalent to the Z score since z = (x - μ) / σ = x for μ = 0 and σ = 1.

In another example, a raw score of 1600 from a distribution with mean 1000 and variance 90,000 is given. How do we find the Z score? First, convert the variance (σ 2 ) to standard deviation (σ) by taking its square root : σ = √90000 = 300. Then the solution is simply:

z = (1600 - 1000) / 300 = 600 / 300 = 2

This tells us that the raw score of 1600 is 2 standard deviations away from the mean. The normal CDF can then be used to arrive at whatever area under the standard normal curve is of interest. For example, to reject the hypothesis that the true value related to the observation is not lower than or equal to zero, one needs to compute

p = P(X > z) = P(X > 2) = 0.0228

which is the 2.28% percentile. For the last part one can look up the Z table for the row where Z = 2, or use a Z score probability calculator if the value is not tabulated or a greater precision is needed.

    References

1 Gauss, C.F. (1809) "Theoria motvs corporvm coelestivm in sectionibvs conicis Solem ambientivm" [Theory of the Motion of the Heavenly Bodies Moving about the Sun in Conic Sections]

2 Laplace, P-S (1774). "Mémoire sur la probabilité des causes par les événements". Mémoires de l'Académie Royale des Sciences de Paris (Savants étrangers), Tome 6: 621–656. Translated by Stephen M. Stigler in Statistical Science 1(3), 1986.

3 Laplace, P-S (1812). "Théorie analytique des probabilités" [Analytical theory of probabilities]

4 Mayo D.G., Spanos A. (2010) – "Error Statistics", in P. S. Bandyopadhyay & M. R. Forster (Eds.), Philosophy of Statistics, (7, 152–198). Handbook of the Philosophy of Science . The Netherlands: Elsevier.

Cite this calculator & page

If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "Z Score Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/z-score-calculator.php URL [Accessed Date: 25 Oct, 2024].

Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:

The author of this tool

     Statistical calculators

Z-test for One Population Mean

Instructions: This calculator conducts a Z-test for one population mean (\(\mu\)), with known population standard deviation (\(\sigma\)). Please select the null and alternative hypotheses, type the hypothesized mean, the significance level, the sample mean, the population standard deviation, and the sample size, and the results of the z-test will be displayed for you:

How to Conduct a Z-Test for One Population Mean?

More about the z-test for one mean so you can better interpret the results obtained by this solver: A z-test for one mean is a hypothesis test that attempts to make a claim about the population mean (\(\mu\)).

The test has two non-overlapping hypotheses, the null and the alternative hypothesis. The null hypothesis is a statement about the population mean, under the assumption of no effect, and the alternative hypothesis is the complementary hypothesis to the null hypothesis. The main properties of a one sample z-test for one population mean are:

• Depending on our knowledge about the "no effect" situation, the z-test can be two-tailed, left-tailed or right-tailed
• The main principle of hypothesis testing is that the null hypothesis is rejected if the test statistic obtained is sufficiently unlikely under the assumption that the null hypothesis is true
• The p-value is the probability of obtaining sample results as extreme or more extreme than the sample results obtained, under the assumption that the null hypothesis is true
• In a hypothesis tests there are two types of errors. Type I error occurs when we reject a true null hypothesis, and the Type II error occurs when we fail to reject a false null hypothesis

Uses of this z-test calculator

What can you do with this z-test statistic calculator for hypothesis testing? The formula for a z-statistic is

The null hypothesis is rejected when the z-statistic lies on the rejection region, which is determined by the significance level (\(\alpha\)) and the type of tail (two-tailed, left-tailed or right-tailed).

What if the population standard deviation is not known?

It frequently happens that you don't actually know the population standard deviation, in which case you need to use a t-test for one mean calculator instead, which adjusts for that by using the sample standard deviation, by using a slightly different distribution (the t-distribution)

How to calculate p-value in the context of a z-test?

The answer depends on whether you are using a two-tailed, a left-tailed or a right-tailed test. Say you have the calculated z-statistic, \(Z_{obs}\).

• For a two-tailed test, the p-value is computed as: \(p = \Pr( Z > |Z_{obs}|) \)
• For a left-tailed test, the p-value is computed as: \(p = \Pr( Z < Z_{obs}) \)
• For a right-tailed test, the p-value is computed as: \(p = \Pr( Z > Z_{obs}) \)

where \(Z\) has a standard normal distribution.

Other types of Z-calculators

In case that you need to compare two population means, when you know the corresponding population standard deviations, you need to use this z-test for two means with known population standard deviations instead.

Outlier Detection

Don't forget to detect outliers before running a z-test for one mean. It is important that outliers are detected and removed before conducting the test, but the results of the test statistics may be slanted.

Example: Application of the Z-test calculator

Question : Assume that you want to test whether or not the population mean is 12.3. You collect a representative random sample of size n = 16, and you find that the sample mean is 11.3. Also, you know that the population is 2.3. Do the sample data provide enough evidence to reject the claim that the population mean is 12.3? Use a two-tailed test, with a significance level of 0.01.

The following information has been provided:

(1) Null and Alternative Hypotheses

The following null and alternative hypotheses need to be tested:

This corresponds to a two-tailed test, for which a z-test for one mean, with known population standard deviation will be used.

(2) Rejection Region

Based on the information provided, the significance level is \(\alpha = 0.01\), and the critical value for a two-tailed test is \(z_c = 2.58\).

The rejection region for this two-tailed test is \(R = \{z: |z| > 2.576\}\)

(3) Test Statistics

The z-statistic is computed as follows:

(4) Decision about the null hypothesis

Since it is observed that \(|z| = 1.739 \le z_c = 2.576\), it is then concluded that the null hypothesis is not rejected.

Using the P-value approach: The p-value is \(p = 0.082\), and since \(p = 0.082 \ge 0.01\), it is concluded that the null hypothesis is not rejected.

(5) Conclusion

It is concluded that the null hypothesis Ho is not rejected. Therefore, there is not enough evidence to claim that the population mean \(\mu\) is different than 12.3, at the \(\alpha = 0.01\) significance level.

Confidence Interval

The 99% confidence interval is \(9.819 < \mu < 12.781\).

Related Calculators

log in to your account

Reset password.

Best Online Statistics Calculators and Tutorials

Z-test calculator.

This z-test calculator is very similar to the z-test function on the TI 84 calculator for conducting hypothesis tests when the population standard deviation is known. In addition to calculating the p-value and z-score of the test statistic, this calculator will also ask for a level of significance and provide a conclusion and analysis. The analysis will also explain which type of error, type I or type II, is possible and interpret what that error means. To get started, enter the population mean, population standard deviation, sample mean, sample size, direction, and level of significance.

$\mu_{0}$: * Population mean in the null hypothesis

$\sigma$ * Population standard deviation

$\bar{x}$: * Mean of the sample

$n$: * Size of the sample

Direction * Left (less than), right (greater than), or bidirectional (≠) Less than Greater than > Unequal to ≠

$\alpha$: * Level of significance

• Salary & Income Tax Calculators
• Mortgage Calculators
• Retirement Calculators
• Depreciation Calculators
• Statistics and Analysis Calculators
• Date and Time Calculators
• Contractor Calculators
• Budget & Savings Calculators
• Loan Calculators
• Forex Calculators
• Real Function Calculators
• Engineering Calculators
• Tax Calculators
• Volume Calculators
• 2D Shape Calculators
• 3D Shape Calculators
• Logistics Calculators
• HRM Calculators
• Sales & Investments Calculators
• Grade & GPA Calculators
• Conversion Calculators
• Ratio Calculators
• Sports & Health Calculators
• Other Calculators

Z-Score Calculator

You can use this Z-Score Calculator to calculate the standard normal score (z-score) based on the raw score value, the population mean, and the standard deviation of the population.

How to use the calculator

• Enter the raw score value
• Enter the mean, standard deviation, and click the "Calculate" button to see the results.

Raw Score (x) :

Population Mean (μ) :

Population Standard Deviation (σ) :

Use this online tool to calculate the z-score for a given p-value.

P-value Type: One-tailed Two-tailed

Z-Score Formula

The Z-Score Calculator uses the following formula:

z = (x - μ) / σ

z is the standard score or Z-score,

x is the raw score to be standardized,

μ is the mean of the population,

σ is the standard deviation of the population.

Z-Score Calculation Example

The mean of a dataset is 20 and the standard deviation is 7. Find the z-score for a value of 6.

x = 6, μ = 20, σ = 7

z = (6 - 20) / 7

z = -14 / 7 = -2

Reference: Norman, G. R. and Streiner, D. L., Biostatistics: The Bare Essentials. 2nd edition. London: B.C. Decker, 2000.

• Currently 4.57/5

Rating: 4.6 /5 (538 votes)

A Z-test is a type of statistical hypothesis test used to test the mean of a normally distributed test statistic. It tests whether there is a significant difference between an observed population mean and the population mean under the null hypothesis, H 0 .

A Z-test can only be used when the population variance is known (or can be estimated with a high degree of accuracy), or if the sample size of the experiment is large (typically n>30). Also, the test statistic must exhibit a normal distribution; if it exhibits a distribution that is clearly not normal, the Z-test is not applicable. In many cases, population parameters may not be known, or it may not be possible to estimate them accurately. In such cases, or in cases where the sample size is small, a Student's t-test is more appropriate.

How to conduct a Z-test

The procedure for conducting a Z-test is similar to that of other statistical hypothesis tests, and is generally as follows:

• State the null (H 0 ) and alternative hypotheses (H a ).
• Select a significance level, α.
• Calculate the Z-score.
• Determine the critical value(s) of Z or the p-value.
• Compare the Z-score of the observed value to the critical value of Z (or compare the p-value to α) to determine if the null hypothesis should be rejected in favor of the alternative hypothesis, or if the null hypothesis should not be rejected.

H 0 and H a

The null hypothesis is typically a statement of no difference. For example, assume that the average score received on the SAT by high schoolers in a given state was a 1200 with a known standard deviation. If the average score of students in a given high school is a 1230, we may use a Z-test to determine whether this result is better, statistically, than the state average. The null hypothesis in this case would be that the average score of students in the high school is not better than the state average, or H 0 : μ ≤ μ 0 , or μ ≤ 1200.

The alternative hypothesis is a statement of difference from the null hypothesis. It can take one of three forms:

• Given H 0 : μ ≤ μ 0 , H a : μ > μ 0
• Given H 0 : μ ≥ μ 0 , H a : μ 0
• Given H 0 : μ = μ 0 , H a : μ ≠ μ 0

In this example, it is believed that a score of 1230 is statistically significant, and that students in this high school performed better than the state average. Therefore, the alternative hypothesis takes on the first form in the list, H a : μ > μ 0 , or μ > 1200.

Significance level

The significance level, α, is the probability of a study rejecting the null hypothesis when the null hypothesis is true. Commonly used significance levels include 0.01, 0.05, and 0.10. A significance level of 0.05, or 5%, means that there is a 5% chance of concluding that a difference exists (thus rejecting H 0 ) when there is no actual difference. The lower the significance level, the more evidence required before the null hypothesis can be rejected. The significance level is compared to the p-value: if a p-value is less than the significance level, the null hypothesis is rejected in favor of the alternative hypothesis.

Calculating a Z-score is a necessary part of conducting a Z-test. A Z-score indicates the number of standard deviations that an observed value is from the mean in a standard normal distribution. For example, an observed value with a Z-score of 1.2 indicates that the observed value is 1.2 standard deviations from the mean. If the population mean and standard deviation are known, the Z-score is calculated using the following formula:

where μ is the mean of the population, σ is the standard deviation of the population, and x is the observed value. In many cases the population mean and standard deviation are not known. In such cases, these population parameters can be estimated using a sample mean and sample standard deviation, and the Z-score can be computed as follows:

where x is the sample mean, s is the sample standard deviation, and x is the observed value.

Critical value and p-value

Once a Z-score has been calculated, there are two methods for drawing conclusions about the test statistic: using the critical value(s), or using a p-value. To form a conclusion for a hypothesis test using a critical value, the Z-score of the observed value is compared to the critical value(s) of the selected significance level; to use a p-value, the p-value of the observed value is compared to the significance level.

Critical value

A critical value is a value that indicates the critical region(s) (or rejection region) of the standard normal distribution, where a critical region is the area of the distribution in which a value must lie in order to reject the null hypothesis.

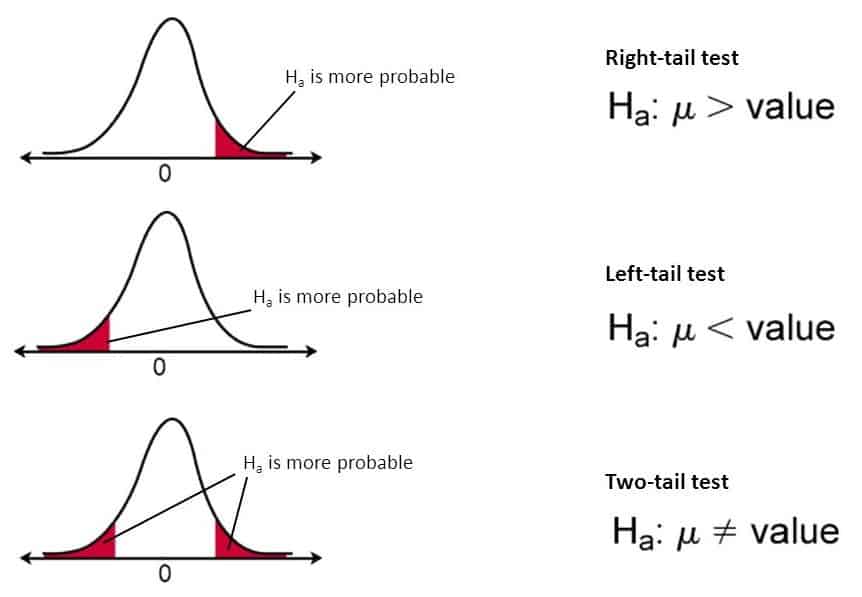
The critical value is dependent on the significance level as well as whether a one-tailed or two-tailed test is being conducted. A one-tailed test is used when we want to know if a value is significantly larger or smaller than the Z-score. There is only one critical region in a one-tailed Z-test. It is either a left-tailed test (or lower-tailed) or right-tailed test (or upper-tailed) based on the position of the critical region, as shown in the figure below.

The critical regions are shown in pink. If a test statistic lies within the pink region, the null hypothesis is rejected in favor of the alternative hypothesis. Otherwise, the null hypothesis is not rejected.

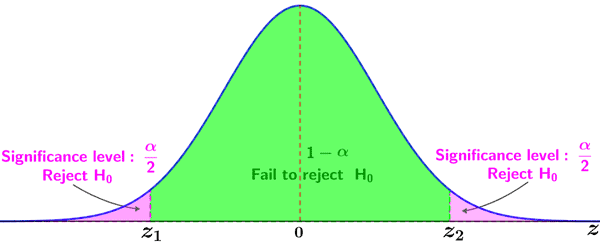
If a test value lies in either of the critical regions shown in pink, the null hypothesis is rejected in favor of the alternative hypothesis; if it lies within the green region, the null hypothesis is not rejected.

After selecting the significance level and type of test, the critical Z value can be determined using a Z table by finding the Z value that corresponds to the selected significance level. For example, for a one-tailed test and a significance level of 0.05, find the probability closest to 0.05 and read the Z value that results in this probability; the Z value for α = 0.05 for a one-tailed Z-test is -1.96 for a left-tailed Z-test and 1.96 for a right-tailed Z-test. For a two-tailed Z-test, divide α by 2, then determine the corresponding Z-value. For α = 0.05, each tail will comprise an area of 0.025 in the standard normal distribution, which corresponds to Z-values of -1.645 and 1.645. Thus, the critical regions are Z 1.645. The critical values for common significance levels are shown in the table below:

The p-value indicates the probability of obtaining test results that are at least as extreme as the observed results, assuming that the null hypothesis is true. It tells us how likely it is for an outcome to occur solely based on chance. For example, a p-value of 0.05 means that there is a 5% chance that an outcome occurred solely by chance. The smaller the p-value, the less likely it is for an outcome to occur solely by chance, and the more evidence there is to reject the null hypothesis.

Like critical values, a p-value can be determined using a Z table. For a left-tailed Z-test, the p-value is the area under the standard normal distribution to the left of the Z-score of the observed value; for a right-tailed Z-test, it is the area to the right of the Z-score; for a two-tailed Z-test, it is the sum of the area to the left and right of the Z-score. If the p-value is less than or equal to the significance level, the null hypothesis is rejected in favor of the alternative hypothesis. Otherwise, the null hypothesis is not rejected.

It is important to note that the p-value is not the probability that the null hypothesis is true. It is the probability that the data could deviate from the null hypothesis as much, or more than it did. The calculation of the p-value assumes that the null hypothesis is true, so it is not a measure of whether or not the null hypothesis is correct. Rather, it is a measure of how well the data fits the null hypothesis. Also, the p-value (or critical value) may provide evidence that the null hypothesis should be rejected in favor of the alternative hypothesis at the chosen level of significance . This does not mean that the alternative hypothesis is being accepted, because it is possible that the null hypothesis would not be rejected at a different significance level. Similarly, if the p-value is greater than the significance level, this does not mean that the null hypothesis is being accepted, just that the null hypothesis is not rejected.

Finally, p-values and critical values only indicate statistical significance, and may not necessarily indicate that the study's findings are significant within their context. For example, if a new medicine and a placebo are tested on different populations, and the medicine is found to have a statistically significant effect, it may not necessarily mean that there is clinical significance. It is possible for a finding to be both statistically and clinically significant, or only one or the other. For large sample sizes, it is possible for results to indicate statistical significance even when the effect is actually small and unimportant. Conversely, a small sample may not exhibit statistical significance even when the effect is large and potentially important. Thus, it is important to fully understand the scope of a study, as well as the statistical methods used, in order to effectively interpret the results and draw accurate, unbiased conclusions.

The average score on a national mathematics exam taken by high school seniors is an 82 with a standard deviation of 8. A sample of 1000 seniors achieved an average score of 68. Perform a Z-test to determine whether there is a statistically significant difference between the national average and that of the sample of seniors at a significance level of 0.05.

We want to determine whether there is any difference, so the null hypothesis is that there is no difference, or

H 0 : μ = 82

and the alternative hypothesis is:

H a : μ ≠ 82

Thus, a two-tailed Z-test should be conducted since differences on either side of the distribution must be accounted for.

The selected significance level is:

α = 0.05

This value must be greater than the p-value in order to conclude that the difference in scores is statistically significant.

Since the population standard deviation and mean are known, the Z-score can be computed as:

Based on the selected significance level and the use of a two-tailed Z-test, the critical values are Z = ± 1.96. Since the Z-score of the observed value lies between both tails (rather than within one of them), we fail to reject the null hypothesis, as depicted in the figure below.

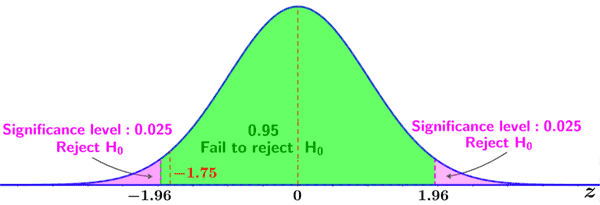
Thus, we conclude that the difference between the observed mean and the population mean is not statistically significant for a significance level of 0.05.

However, had we selected a significance level of 0.10, the critical values would be Z = ±1.645, and Z = -1.75 would lie within the left tail of the distribution. In this case, we would reject the null hypothesis in favor of the alternative hypothesis, and conclude that the observed value is statistically significant for a significance level of 0.10.

The above discussion involved hypothesis testing for one sample, where an observed value was compared to the expected population parameter. In certain cases, scientists may want to compare the means of two samples. In such cases, a two-sample Z-test is used instead.

Two-sample Z-test

A two-sample Z-test is conducted using the same procedures described above for a one-sample Z-test, with the exception that the Z-score is computed using the following formula:

where μ 1 and μ 2 are the means of the two respective populations, x 1 and x 2 are the sample means, and n 1 and n 2 are the sample sizes.

Researchers want to test whether a certain drug has any effect on the scores received by patients who are administered the drug prior to performing a physical stress test. The researchers place patients into 2 groups: 500 are placed into the experimental group and are administered the drug; 300 are placed into the control group and are administered a placebo. Both groups then perform the physical stress test, the results of which are as follows:

Determine whether or not there is a statistically significant difference between the two groups at a significance level of 0.05.

The null hypothesis is that there is no difference, so:

H 0 : μ 1 = μ 2

Also, since it is assumed that the null hypothesis is true, μ 1 - μ 2 = 0.

The alternative hypothesis is that there is a difference, so:

H a : μ 1 ≠ μ 2

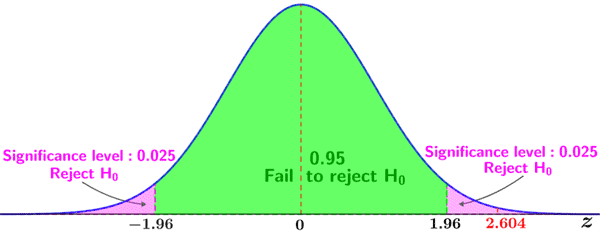
The selected significance level is 0.05, and we conduct a two-tailed test since we are looking for any observable difference.

The Z-score is then calculated as follows:

Using a Z table (or a p-value calculator), the p-value for a two-tailed Z-test for a Z-score of 2.604 is 0.009214. Since the p-value is less than the selected significance level, we reject the null hypothesis in favor of the alternative hypothesis, and conclude that the drug has a statistically significant effect on the performance of the patients. Since the Z-score lies in the right tail, we may conclude that patients who received the drug scored significantly better than those who received the placebo. If the Z-score were to lie in left tail, we would conclude the opposite: that patients who received the drug performed significantly worse.

We could also have used the critical values Z = ±1.96 for a significance level of 0.05 to reach the same conclusion, since 2.604 lies within the critical region denoted by the right tail of the distribution, as shown in the figure below.

Z Table. Z Score Table. Normal Distribution Table. Standard Normal Table.

What is Z-Test?

Z-Test is a statistical test which let’s us approximate the distribution of the test statistic under the null hypothesis using normal distribution .

Z-Test is a test statistic commonly used in hypothesis test when the sample data is large.For carrying out the Z-Test, population parameters such as mean, variance, and standard deviation should be known.

This test is widely used to determine whether the mean of the two samples are different when the variance is known. We make use of the Z score and the Z table for running the Z-Test.

Z-Test as Hypothesis Test

A test statistic is a random variable that we calculate from the sample data to determine whether to reject the null hypothesis. This random variable is used to calculate the P-value, which indicates how strong the evidence is against the null hypothesis. Z-Test is such a test statistic where we make use of the mean value and z score to determine the P-value. Z-Test compares the mean of two large samples taken from a population when the variance is known.

Z-Test is usually used to conduct a hypothesis test when the sample size is greater than 30. This is because of the central limit theorem where when the sample gets larger, the distributed data graph starts resembling a bell curve and is considered to be distributed normally. Since the Z-Test follows normal distribution under the null hypothesis, it is the most suitable test statistic for large sample data.

Why do we use a large sample for conducting a hypothesis test?

In a hypothesis test, we are trying to reject a null hypothesis with the evidence that we should collect from sample data which represents only a portion of the population. When the population has a large size, and the sample data is small, we will not be able to draw an accurate conclusion from the test to prove our null hypothesis is false. As sample data provide us a door to the entire population, it should be large enough for us to arrive at a significant inference. Hence a sufficiently large data should be considered for a hypothesis test especially if the population is huge.

How to Run a Z-Test

Z-Test can be considered as a test statistic for a hypothesis test to calculate the P-value. However, there are certain conditions that should be satisfied by the sample to run the Z-Test.

The conditions are as follows:

• The sample size should be greater than 30.

This is already mentioned above. The size of the sample is an important factor in Z-Testing as the Z-Test follows a normal distribution and so should the data. If the same size is less than 30, it is recommended to use a t-test instead

• All the data point should be independent and doesn’t affect each other.

Each element in the sample, when considered single should be independent and shouldn’t have a relationship with another element.

• The data must be distributed normally.

This is ensured if the sample data is large.

• The sample should be selected randomly from a population.

Each data in the population should have an equal chance to be selected as one of the sample data.

• The sizes of the selected samples should be equal if at all possible.

When considering multiple sample data, ensuring that the size of each sample is the same for an accurate calculation of population parameters.

• The standard deviation of the population is known.

The population parameter, standard deviation must be given to run a Z-Test as we cannot perform the calculation without knowing it. If it is not directly given, then it assumed that the variance of the sample data is equal to the variance of the entire population.

If the conditions are satisfied, the Z-Test can be successfully implemented.

Following are steps to run the Z-Test:

• State the null hypothesis

The null hypothesis is a statement of no effect and it supports the data which is already given. It is generally represented as :

• State the alternate hypothesis

The statement that we are trying to prove is the alternate hypothesis. It is represented as:

This is the representation of a bidirectional alternate hypothesis.

• H 1 :µ > k

This is the representation of a one-directional alternate hypothesis that is represented in the right region of the graph.

• H 1 :µ < k

This is the representation of a one-directional alternate hypothesis that is represented in the left region of the graph.

• Choose an alpha level for the test.

Alpha level or significant level is the probability of rejecting the null hypothesis when it is true. It is represented by ( α ). An alpha level must be chosen wisely so as to avoid the Type I and Type II errors.

If we choose a large alpha value such as 10%, it is likely to reject a null hypothesis when it is true. There is a probability of 10% for us to reject the null hypothesis. This is an error known as the Type I error.

On the other hand, if we choose an alpha level as low as 1%, there is a chance to accept the null hypothesis even if it is false. That is we reject the alternate hypothesis to favor the null hypothesis. This is the Type II error.

Hence the alpha level should be chosen in such a way that the chance of making Type I or Type II error is minimal. For this reason, the alpha level is commonly selected as 5% which is proven best to avoid errors.

• Determining the critical value of Z from the Z table.

The critical value is the point in the normal distribution graph that splits the graph into two regions: the acceptance region and the rejection regions. It can be also described as the extreme value for which a null hypothesis can be accepted. This critical value of Z can be found from the Z table .

• Calculate the test statistic.

The sample data that we choose to test is converted into a single value. This is known as the test statistic. This value is compared to the null value. If the test statistic significantly differs from the null value, the null value is rejected.

• Comparing the test statistic with the critical value.

Now, we have to determine whether the test statistic we have calculated comes under the acceptance region or the rejection region. For this, the test statistic is compared with the critical value to know whether we should accept or reject a null hypothesis.

Types of Z-Test

Z-Test can be used to run a hypothesis test for a single sample or to compare the mean of two samples. There are two common types of Z-Test

One-Sample Z-Test

This is the most basic type of hypothesis test that is widely used. For running an one-sample Z-Test, all we need to know is the mean and standard deviation of the population. We consider only a single sample for a one-sample Z-Test. One-sample Z-Test is used to test whether the population parameter is different from the hypothesized value i.e whether the mean of the population is equal to, less than or greater than the hypothesized value.

The equation for finding the value of Z is:

The following are the assumptions that are generally taken for a one-sampled Z-Test:

• The sample size is equal to or greater than 30.
• One normally distributed sample is considered with the standard deviation known.
• The null hypothesis is that the population mean that is calculated from the sample is equal to the hypothetically determined population mean.

Two-Sample Z-Test

A two-sample Z-Test is used whenever there is a comparison between two independent samples. It is used to check whether the difference between the means is equal to zero or not. Suppose if we want to know whether men or women prefer to drive more in a city, we use a two-sample Z-Test as it is the comparison of two independent samples of men and women.

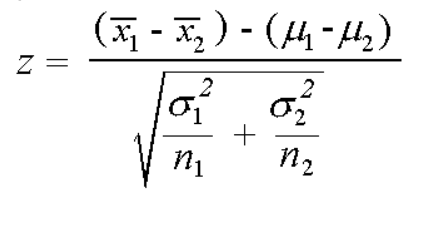
• x 1 and x 2 represent the mean of the two samples.
• µ 1 and µ 2 are the hypothesized mean values.
• σ 1 and σ 2 are the standard deviations.
• n 1 and n 2 are the sizes of the samples.

The following are the assumptions that are generally taken for a two-sample Z-Test:

• Two independent, normally distributed samples are considered for the Z-Test with the standard deviation known.
• Each sample is equal to or greater than 30.
• The null hypothesis is stated that the population mean of the two samples taken does not differ.

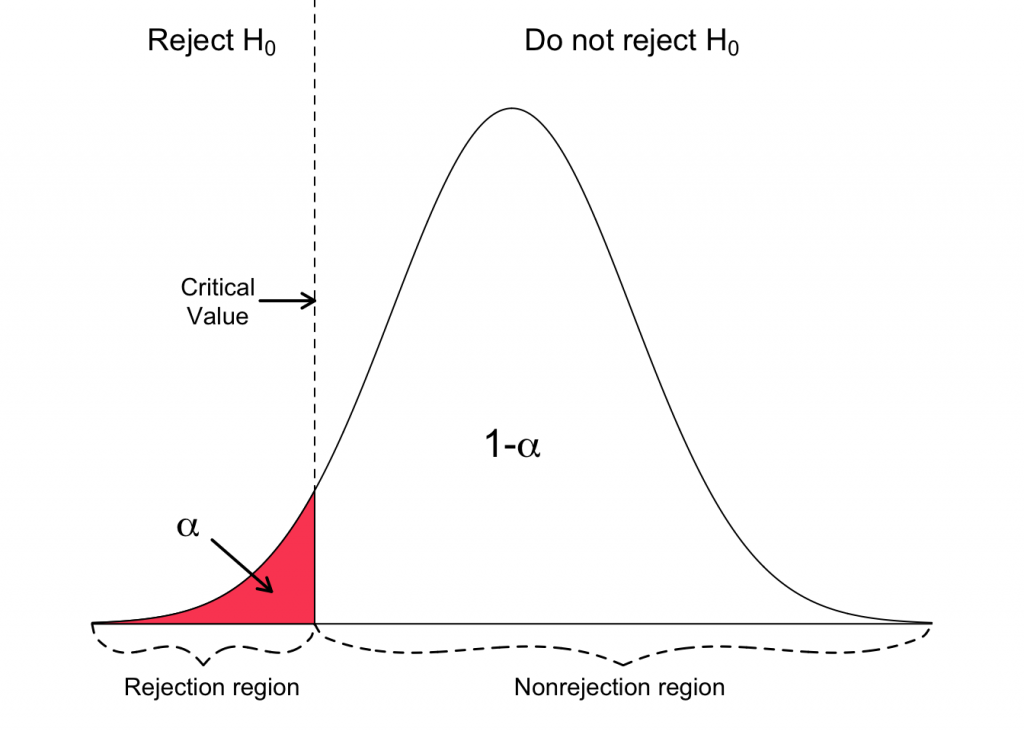
Critical value

A critical value is a line that splits a normally distributed graph into two different sections. Namely the ‘Rejection region’ and ‘Acceptance region’. If your test value falls in the ‘Rejection region’, then the null hypothesis is rejected and if your test value falls in the ‘Accepted region’, then the null hypothesis is accepted.

Critical Value Vs Significant Value

Significant level, alpha is the probability of rejecting a null hypothesis when it is actually true. While the critical value is the extreme value up to which a null hypothesis is true. There migh come a confusion regarding both of these parameters.

Critical value is a value that lies in critical region. It is in fact the boundary value of the rejection region. Also, it is the value up to which the null hypothesis is true. Hence the critical value is considered to be the point at which the null hypothesis is true or is rejected.

Critical value gives a point of extremity whose probability is indicated by the significant level. Significant level is pre-selected for a hypothesis test and critical value is calculated from this Alpha value. Critical value is a point represented as Z score and Significant level is a probability.

Z-Test Vs T-Test

Z-Test are used when the sample size exceeds 30. As Z-Test follows normal distribution, large sample size can be taken for the Z-Test. Z-Test indicates the distance of a data point from the mean of the data set in terms of standard deviation. Also. this test can only be used if the standard deviation of the data set is known.

T-Test is based on T distribution in which the mean value is known and the variance could be calculated from the sample. T-Test is most preferred to know the difference between the statistical parameters of two samples as the standard deviation of the samples are not usually given in a two-sample test for running the Z-Test. Also, if the sample size is less than 30, T-Test is preferred.

p-value Calculator

Table of contents

Welcome to our p-value calculator! You will never again have to wonder how to find the p-value, as here you can determine the one-sided and two-sided p-values from test statistics, following all the most popular distributions: normal, t-Student, chi-squared, and Snedecor's F.

P-values appear all over science, yet many people find the concept a bit intimidating. Don't worry – in this article, we will explain not only what the p-value is but also how to interpret p-values correctly . Have you ever been curious about how to calculate the p-value by hand? We provide you with all the necessary formulae as well!

🙋 If you want to revise some basics from statistics, our normal distribution calculator is an excellent place to start.

What is p-value?

Formally, the p-value is the probability that the test statistic will produce values at least as extreme as the value it produced for your sample . It is crucial to remember that this probability is calculated under the assumption that the null hypothesis H 0 is true !

More intuitively, p-value answers the question:

Assuming that I live in a world where the null hypothesis holds, how probable is it that, for another sample, the test I'm performing will generate a value at least as extreme as the one I observed for the sample I already have?

It is the alternative hypothesis that determines what "extreme" actually means , so the p-value depends on the alternative hypothesis that you state: left-tailed, right-tailed, or two-tailed. In the formulas below, S stands for a test statistic, x for the value it produced for a given sample, and Pr(event | H 0 ) is the probability of an event, calculated under the assumption that H 0 is true:

Left-tailed test: p-value = Pr(S ≤ x | H 0 )

Right-tailed test: p-value = Pr(S ≥ x | H 0 )

Two-tailed test:

p-value = 2 × min{Pr(S ≤ x | H 0 ), Pr(S ≥ x | H 0 )}

(By min{a,b} , we denote the smaller number out of a and b .)

If the distribution of the test statistic under H 0 is symmetric about 0 , then: p-value = 2 × Pr(S ≥ |x| | H 0 )

or, equivalently: p-value = 2 × Pr(S ≤ -|x| | H 0 )

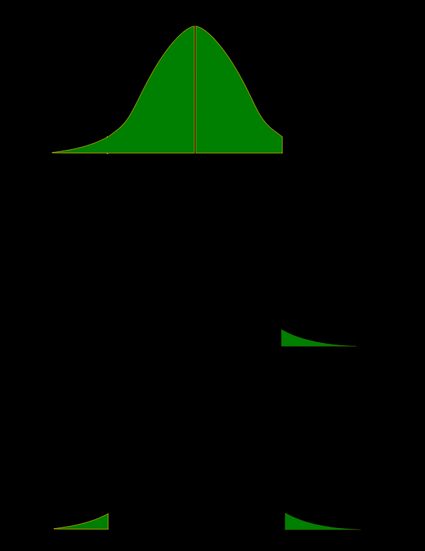
As a picture is worth a thousand words, let us illustrate these definitions. Here, we use the fact that the probability can be neatly depicted as the area under the density curve for a given distribution. We give two sets of pictures: one for a symmetric distribution and the other for a skewed (non-symmetric) distribution.

• Symmetric case: normal distribution:

• Non-symmetric case: chi-squared distribution:

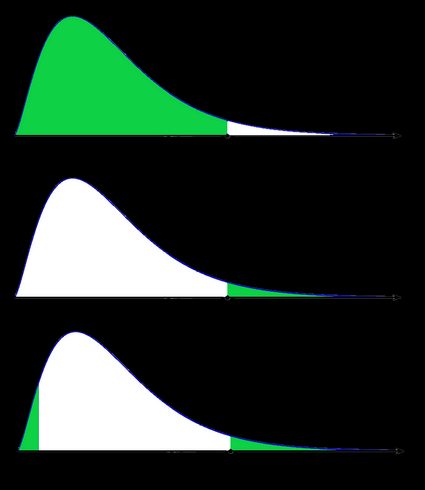
In the last picture (two-tailed p-value for skewed distribution), the area of the left-hand side is equal to the area of the right-hand side.

How do I calculate p-value from test statistic?

To determine the p-value, you need to know the distribution of your test statistic under the assumption that the null hypothesis is true . Then, with the help of the cumulative distribution function ( cdf ) of this distribution, we can express the probability of the test statistics being at least as extreme as its value x for the sample:

Left-tailed test:

p-value = cdf(x) .

Right-tailed test:

p-value = 1 - cdf(x) .

p-value = 2 × min{cdf(x) , 1 - cdf(x)} .

If the distribution of the test statistic under H 0 is symmetric about 0 , then a two-sided p-value can be simplified to p-value = 2 × cdf(-|x|) , or, equivalently, as p-value = 2 - 2 × cdf(|x|) .

The probability distributions that are most widespread in hypothesis testing tend to have complicated cdf formulae, and finding the p-value by hand may not be possible. You'll likely need to resort to a computer or to a statistical table, where people have gathered approximate cdf values.

Well, you now know how to calculate the p-value, but… why do you need to calculate this number in the first place? In hypothesis testing, the p-value approach is an alternative to the critical value approach . Recall that the latter requires researchers to pre-set the significance level, α, which is the probability of rejecting the null hypothesis when it is true (so of type I error ). Once you have your p-value, you just need to compare it with any given α to quickly decide whether or not to reject the null hypothesis at that significance level, α. For details, check the next section, where we explain how to interpret p-values.

How to interpret p-value

As we have mentioned above, the p-value is the answer to the following question:

What does that mean for you? Well, you've got two options:

• A high p-value means that your data is highly compatible with the null hypothesis; and
• A small p-value provides evidence against the null hypothesis , as it means that your result would be very improbable if the null hypothesis were true.

However, it may happen that the null hypothesis is true, but your sample is highly unusual! For example, imagine we studied the effect of a new drug and got a p-value of 0.03 . This means that in 3% of similar studies, random chance alone would still be able to produce the value of the test statistic that we obtained, or a value even more extreme, even if the drug had no effect at all!

The question "what is p-value" can also be answered as follows: p-value is the smallest level of significance at which the null hypothesis would be rejected. So, if you now want to make a decision on the null hypothesis at some significance level α , just compare your p-value with α :

• If p-value ≤ α , then you reject the null hypothesis and accept the alternative hypothesis; and
• If p-value ≥ α , then you don't have enough evidence to reject the null hypothesis.

Obviously, the fate of the null hypothesis depends on α . For instance, if the p-value was 0.03 , we would reject the null hypothesis at a significance level of 0.05 , but not at a level of 0.01 . That's why the significance level should be stated in advance and not adapted conveniently after the p-value has been established! A significance level of 0.05 is the most common value, but there's nothing magical about it. Here, you can see what too strong a faith in the 0.05 threshold can lead to. It's always best to report the p-value, and allow the reader to make their own conclusions.

Also, bear in mind that subject area expertise (and common reason) is crucial. Otherwise, mindlessly applying statistical principles, you can easily arrive at statistically significant, despite the conclusion being 100% untrue.

How to use the p-value calculator to find p-value from test statistic

As our p-value calculator is here at your service, you no longer need to wonder how to find p-value from all those complicated test statistics! Here are the steps you need to follow:

Pick the alternative hypothesis : two-tailed, right-tailed, or left-tailed.

Tell us the distribution of your test statistic under the null hypothesis: is it N(0,1), t-Student, chi-squared, or Snedecor's F? If you are unsure, check the sections below, as they are devoted to these distributions.

If needed, specify the degrees of freedom of the test statistic's distribution.

Enter the value of test statistic computed for your data sample.

By default, the calculator uses the significance level of 0.05.

Our calculator determines the p-value from the test statistic and provides the decision to be made about the null hypothesis.

How do I find p-value from z-score?

In terms of the cumulative distribution function (cdf) of the standard normal distribution, which is traditionally denoted by Φ , the p-value is given by the following formulae:

Left-tailed z-test:

p-value = Φ(Z score )

Right-tailed z-test:

p-value = 1 - Φ(Z score )

Two-tailed z-test:

p-value = 2 × Φ(−|Z score |)

p-value = 2 - 2 × Φ(|Z score |)

🙋 To learn more about Z-tests, head to Omni's Z-test calculator .

We use the Z-score if the test statistic approximately follows the standard normal distribution N(0,1) . Thanks to the central limit theorem, you can count on the approximation if you have a large sample (say at least 50 data points) and treat your distribution as normal.

A Z-test most often refers to testing the population mean , or the difference between two population means, in particular between two proportions. You can also find Z-tests in maximum likelihood estimations.

How do I find p-value from t?

The p-value from the t-score is given by the following formulae, in which cdf t,d stands for the cumulative distribution function of the t-Student distribution with d degrees of freedom:

Left-tailed t-test:

p-value = cdf t,d (t score )

Right-tailed t-test:

p-value = 1 - cdf t,d (t score )

Two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

p-value = 2 - 2 × cdf t,d (|t score |)

Use the t-score option if your test statistic follows the t-Student distribution . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails – the exact shape depends on the parameter called the degrees of freedom . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from the normal distribution N(0,1).

The most common t-tests are those for population means with an unknown population standard deviation, or for the difference between means of two populations , with either equal or unequal yet unknown population standard deviations. There's also a t-test for paired (dependent) samples .

🙋 To get more insights into t-statistics, we recommend using our t-test calculator .

p-value from chi-square score (χ² score)

Use the χ²-score option when performing a test in which the test statistic follows the χ²-distribution .

This distribution arises if, for example, you take the sum of squared variables, each following the normal distribution N(0,1). Remember to check the number of degrees of freedom of the χ²-distribution of your test statistic!

How to find the p-value from chi-square-score ? You can do it with the help of the following formulae, in which cdf χ²,d denotes the cumulative distribution function of the χ²-distribution with d degrees of freedom:

Left-tailed χ²-test:

p-value = cdf χ²,d (χ² score )

Right-tailed χ²-test:

p-value = 1 - cdf χ²,d (χ² score )

Remember that χ²-tests for goodness-of-fit and independence are right-tailed tests! (see below)

Two-tailed χ²-test:

p-value = 2 × min{cdf χ²,d (χ² score ), 1 - cdf χ²,d (χ² score )}

(By min{a,b} , we denote the smaller of the numbers a and b .)

The most popular tests which lead to a χ²-score are the following:

Testing whether the variance of normally distributed data has some pre-determined value. In this case, the test statistic has the χ²-distribution with n - 1 degrees of freedom, where n is the sample size. This can be a one-tailed or two-tailed test .

Goodness-of-fit test checks whether the empirical (sample) distribution agrees with some expected probability distribution. In this case, the test statistic follows the χ²-distribution with k - 1 degrees of freedom, where k is the number of classes into which the sample is divided. This is a right-tailed test .

Independence test is used to determine if there is a statistically significant relationship between two variables. In this case, its test statistic is based on the contingency table and follows the χ²-distribution with (r - 1)(c - 1) degrees of freedom, where r is the number of rows, and c is the number of columns in this contingency table. This also is a right-tailed test .

p-value from F-score

Finally, the F-score option should be used when you perform a test in which the test statistic follows the F-distribution , also known as the Fisher–Snedecor distribution. The exact shape of an F-distribution depends on two degrees of freedom .

To see where those degrees of freedom come from, consider the independent random variables X and Y , which both follow the χ²-distributions with d 1 and d 2 degrees of freedom, respectively. In that case, the ratio (X/d 1 )/(Y/d 2 ) follows the F-distribution, with (d 1 , d 2 ) -degrees of freedom. For this reason, the two parameters d 1 and d 2 are also called the numerator and denominator degrees of freedom .

The p-value from F-score is given by the following formulae, where we let cdf F,d1,d2 denote the cumulative distribution function of the F-distribution, with (d 1 , d 2 ) -degrees of freedom:

Left-tailed F-test:

p-value = cdf F,d1,d2 (F score )

Right-tailed F-test:

p-value = 1 - cdf F,d1,d2 (F score )

Two-tailed F-test:

p-value = 2 × min{cdf F,d1,d2 (F score ), 1 - cdf F,d1,d2 (F score )}

Below we list the most important tests that produce F-scores. All of them are right-tailed tests .

A test for the equality of variances in two normally distributed populations . Its test statistic follows the F-distribution with (n - 1, m - 1) -degrees of freedom, where n and m are the respective sample sizes.

ANOVA is used to test the equality of means in three or more groups that come from normally distributed populations with equal variances. We arrive at the F-distribution with (k - 1, n - k) -degrees of freedom, where k is the number of groups, and n is the total sample size (in all groups together).

A test for overall significance of regression analysis . The test statistic has an F-distribution with (k - 1, n - k) -degrees of freedom, where n is the sample size, and k is the number of variables (including the intercept).

With the presence of the linear relationship having been established in your data sample with the above test, you can calculate the coefficient of determination, R 2 , which indicates the strength of this relationship . You can do it by hand or use our coefficient of determination calculator .

A test to compare two nested regression models . The test statistic follows the F-distribution with (k 2 - k 1 , n - k 2 ) -degrees of freedom, where k 1 and k 2 are the numbers of variables in the smaller and bigger models, respectively, and n is the sample size.

You may notice that the F-test of an overall significance is a particular form of the F-test for comparing two nested models: it tests whether our model does significantly better than the model with no predictors (i.e., the intercept-only model).

Can p-value be negative?

No, the p-value cannot be negative. This is because probabilities cannot be negative, and the p-value is the probability of the test statistic satisfying certain conditions.

What does a high p-value mean?

A high p-value means that under the null hypothesis, there's a high probability that for another sample, the test statistic will generate a value at least as extreme as the one observed in the sample you already have. A high p-value doesn't allow you to reject the null hypothesis.

What does a low p-value mean?

A low p-value means that under the null hypothesis, there's little probability that for another sample, the test statistic will generate a value at least as extreme as the one observed for the sample you already have. A low p-value is evidence in favor of the alternative hypothesis – it allows you to reject the null hypothesis.

What do you want?

What do you know?

Your Z-score

Z-score : the test statistic follows the standard normal distribution N(0,1).

.css-m482sy.css-m482sy{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-m482sy.css-m482sy:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-m482sy .js-external-link-button.link-like,.css-m482sy .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-m482sy .js-external-link-button.link-like:hover,.css-m482sy .js-external-link-anchor:hover,.css-m482sy .js-external-link-button.link-like:active,.css-m482sy .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-m482sy .js-external-link-button.link-like:focus-visible,.css-m482sy .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-m482sy p,.css-m482sy div{margin:0;display:block;}.css-m482sy pre{margin:0;display:block;}.css-m482sy pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-m482sy pre:not(:first-child){padding-top:8px;}.css-m482sy ul,.css-m482sy ol{display:block margin:0;padding-left:20px;}.css-m482sy ul li,.css-m482sy ol li{padding-top:8px;}.css-m482sy ul ul,.css-m482sy ol ul,.css-m482sy ul ol,.css-m482sy ol ol{padding-top:0;}.css-m482sy ul:not(:first-child),.css-m482sy ol:not(:first-child){padding-top:4px;} .css-63uqft{margin:auto;background-color:white;overflow:auto;overflow-wrap:break-word;word-break:break-word;}.css-63uqft code,.css-63uqft kbd,.css-63uqft pre,.css-63uqft samp{font-family:monospace;}.css-63uqft code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-63uqft figcaption,.css-63uqft caption{text-align:center;}.css-63uqft figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-63uqft h3{font-size:1.75rem;}.css-63uqft h4{font-size:1.5rem;}.css-63uqft .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-63uqft .mathBlock .katex{font-size:24px;text-align:left;}.css-63uqft .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-63uqft .videoBlock,.css-63uqft .imageBlock{margin-bottom:16px;}.css-63uqft .imageBlock__image-align--left,.css-63uqft .videoBlock__video-align--left{float:left;}.css-63uqft .imageBlock__image-align--right,.css-63uqft .videoBlock__video-align--right{float:right;}.css-63uqft .imageBlock__image-align--center,.css-63uqft .videoBlock__video-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-63uqft .imageBlock__image-align--none,.css-63uqft .videoBlock__video-align--none{clear:both;margin-left:0;margin-right:0;}.css-63uqft .videoBlock__video--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-63uqft .videoBlock__video--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-63uqft .videoBlock__caption{text-align:left;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-63uqft .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-63uqft .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-63uqft .katex .katex-version::after{content:'0.13.13';}.css-63uqft .katex .katex-mathml{position:absolute;clip:rect(1px,1px,1px,1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-63uqft .katex .katex-html>.newline{display:block;}.css-63uqft .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-63uqft .katex .strut{display:inline-block;}.css-63uqft .katex .textbf{font-weight:bold;}.css-63uqft .katex .textit{font-style:italic;}.css-63uqft .katex .textrm{font-family:KaTeX_Main;}.css-63uqft .katex .textsf{font-family:KaTeX_SansSerif;}.css-63uqft .katex .texttt{font-family:KaTeX_Typewriter;}.css-63uqft .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-63uqft .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-63uqft .katex .mathrm{font-style:normal;}.css-63uqft .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-63uqft .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-63uqft .katex .amsrm{font-family:KaTeX_AMS;}.css-63uqft .katex .mathbb,.css-63uqft .katex .textbb{font-family:KaTeX_AMS;}.css-63uqft .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-63uqft .katex .mathfrak,.css-63uqft .katex .textfrak{font-family:KaTeX_Fraktur;}.css-63uqft .katex .mathtt{font-family:KaTeX_Typewriter;}.css-63uqft .katex .mathscr,.css-63uqft .katex .textscr{font-family:KaTeX_Script;}.css-63uqft .katex .mathsf,.css-63uqft .katex .textsf{font-family:KaTeX_SansSerif;}.css-63uqft .katex .mathboldsf,.css-63uqft .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-63uqft .katex .mathitsf,.css-63uqft .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-63uqft .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-63uqft .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-63uqft .katex .vlist-r{display:table-row;}.css-63uqft .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-63uqft .katex .vlist>span{display:block;height:0;position:relative;}.css-63uqft .katex .vlist>span>span{display:inline-block;}.css-63uqft .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-63uqft .katex .vlist-t2{margin-right:-2px;}.css-63uqft .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-63uqft .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-63uqft .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-63uqft .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-63uqft .katex .msupsub{text-align:left;}.css-63uqft .katex .mfrac>span>span{text-align:center;}.css-63uqft .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-63uqft .katex .mfrac .frac-line,.css-63uqft .katex .overline .overline-line,.css-63uqft .katex .underline .underline-line,.css-63uqft .katex .hline,.css-63uqft .katex .hdashline,.css-63uqft .katex .rule{min-height:1px;}.css-63uqft .katex .mspace{display:inline-block;}.css-63uqft .katex .llap,.css-63uqft .katex .rlap,.css-63uqft .katex .clap{width:0;position:relative;}.css-63uqft .katex .llap>.inner,.css-63uqft .katex .rlap>.inner,.css-63uqft .katex .clap>.inner{position:absolute;}.css-63uqft .katex .llap>.fix,.css-63uqft .katex .rlap>.fix,.css-63uqft .katex .clap>.fix{display:inline-block;}.css-63uqft .katex .llap>.inner{right:0;}.css-63uqft .katex .rlap>.inner,.css-63uqft .katex .clap>.inner{left:0;}.css-63uqft .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-63uqft .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-63uqft .katex .overline .overline-line,.css-63uqft .katex .underline .underline-line,.css-63uqft .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-63uqft .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-63uqft .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-63uqft .katex .sizing.reset-size1.size1,.css-63uqft .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-63uqft .katex .sizing.reset-size1.size2,.css-63uqft .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-63uqft .katex .sizing.reset-size1.size3,.css-63uqft .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-63uqft .katex .sizing.reset-size1.size4,.css-63uqft .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-63uqft .katex .sizing.reset-size1.size5,.css-63uqft .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-63uqft .katex .sizing.reset-size1.size6,.css-63uqft .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-63uqft .katex .sizing.reset-size1.size7,.css-63uqft .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-63uqft .katex .sizing.reset-size1.size8,.css-63uqft .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-63uqft .katex .sizing.reset-size1.size9,.css-63uqft .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-63uqft .katex .sizing.reset-size1.size10,.css-63uqft .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-63uqft .katex .sizing.reset-size1.size11,.css-63uqft .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-63uqft .katex .sizing.reset-size2.size1,.css-63uqft .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-63uqft .katex .sizing.reset-size2.size2,.css-63uqft .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-63uqft .katex .sizing.reset-size2.size3,.css-63uqft .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-63uqft .katex .sizing.reset-size2.size4,.css-63uqft .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-63uqft .katex .sizing.reset-size2.size5,.css-63uqft .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-63uqft .katex .sizing.reset-size2.size6,.css-63uqft .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-63uqft .katex .sizing.reset-size2.size7,.css-63uqft .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-63uqft .katex .sizing.reset-size2.size8,.css-63uqft .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-63uqft .katex .sizing.reset-size2.size9,.css-63uqft .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-63uqft .katex .sizing.reset-size2.size10,.css-63uqft .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-63uqft .katex .sizing.reset-size2.size11,.css-63uqft .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-63uqft .katex .sizing.reset-size3.size1,.css-63uqft .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-63uqft .katex .sizing.reset-size3.size2,.css-63uqft .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-63uqft .katex .sizing.reset-size3.size3,.css-63uqft .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-63uqft .katex .sizing.reset-size3.size4,.css-63uqft .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-63uqft .katex .sizing.reset-size3.size5,.css-63uqft .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-63uqft .katex .sizing.reset-size3.size6,.css-63uqft .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-63uqft .katex .sizing.reset-size3.size7,.css-63uqft .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-63uqft .katex .sizing.reset-size3.size8,.css-63uqft .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-63uqft .katex .sizing.reset-size3.size9,.css-63uqft .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-63uqft .katex .sizing.reset-size3.size10,.css-63uqft .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-63uqft .katex .sizing.reset-size3.size11,.css-63uqft .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-63uqft .katex .sizing.reset-size4.size1,.css-63uqft .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-63uqft .katex .sizing.reset-size4.size2,.css-63uqft .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-63uqft .katex .sizing.reset-size4.size3,.css-63uqft .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-63uqft .katex .sizing.reset-size4.size4,.css-63uqft .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-63uqft .katex .sizing.reset-size4.size5,.css-63uqft .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-63uqft .katex .sizing.reset-size4.size6,.css-63uqft .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-63uqft .katex .sizing.reset-size4.size7,.css-63uqft .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-63uqft .katex .sizing.reset-size4.size8,.css-63uqft .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-63uqft .katex .sizing.reset-size4.size9,.css-63uqft .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-63uqft .katex .sizing.reset-size4.size10,.css-63uqft .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-63uqft .katex .sizing.reset-size4.size11,.css-63uqft .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-63uqft .katex .sizing.reset-size5.size1,.css-63uqft .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-63uqft .katex .sizing.reset-size5.size2,.css-63uqft .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-63uqft .katex .sizing.reset-size5.size3,.css-63uqft .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-63uqft .katex .sizing.reset-size5.size4,.css-63uqft .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-63uqft .katex .sizing.reset-size5.size5,.css-63uqft .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-63uqft .katex .sizing.reset-size5.size6,.css-63uqft .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-63uqft .katex .sizing.reset-size5.size7,.css-63uqft .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-63uqft .katex .sizing.reset-size5.size8,.css-63uqft .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-63uqft .katex .sizing.reset-size5.size9,.css-63uqft .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-63uqft .katex .sizing.reset-size5.size10,.css-63uqft .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-63uqft .katex .sizing.reset-size5.size11,.css-63uqft .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-63uqft .katex .sizing.reset-size6.size1,.css-63uqft .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-63uqft .katex .sizing.reset-size6.size2,.css-63uqft .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-63uqft .katex .sizing.reset-size6.size3,.css-63uqft .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-63uqft .katex .sizing.reset-size6.size4,.css-63uqft .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-63uqft .katex .sizing.reset-size6.size5,.css-63uqft .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-63uqft .katex .sizing.reset-size6.size6,.css-63uqft .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-63uqft .katex .sizing.reset-size6.size7,.css-63uqft .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-63uqft .katex .sizing.reset-size6.size8,.css-63uqft .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-63uqft .katex .sizing.reset-size6.size9,.css-63uqft .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-63uqft .katex .sizing.reset-size6.size10,.css-63uqft .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-63uqft .katex .sizing.reset-size6.size11,.css-63uqft .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-63uqft .katex .sizing.reset-size7.size1,.css-63uqft .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-63uqft .katex .sizing.reset-size7.size2,.css-63uqft .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-63uqft .katex .sizing.reset-size7.size3,.css-63uqft .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-63uqft .katex .sizing.reset-size7.size4,.css-63uqft .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-63uqft .katex .sizing.reset-size7.size5,.css-63uqft .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-63uqft .katex .sizing.reset-size7.size6,.css-63uqft .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-63uqft .katex .sizing.reset-size7.size7,.css-63uqft .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-63uqft .katex .sizing.reset-size7.size8,.css-63uqft .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-63uqft .katex .sizing.reset-size7.size9,.css-63uqft .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-63uqft .katex .sizing.reset-size7.size10,.css-63uqft .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-63uqft .katex .sizing.reset-size7.size11,.css-63uqft .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-63uqft .katex .sizing.reset-size8.size1,.css-63uqft .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-63uqft .katex .sizing.reset-size8.size2,.css-63uqft .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-63uqft .katex .sizing.reset-size8.size3,.css-63uqft .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-63uqft .katex .sizing.reset-size8.size4,.css-63uqft .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-63uqft .katex .sizing.reset-size8.size5,.css-63uqft .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-63uqft .katex .sizing.reset-size8.size6,.css-63uqft .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-63uqft .katex .sizing.reset-size8.size7,.css-63uqft .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-63uqft .katex .sizing.reset-size8.size8,.css-63uqft .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-63uqft .katex .sizing.reset-size8.size9,.css-63uqft .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-63uqft .katex .sizing.reset-size8.size10,.css-63uqft .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-63uqft .katex .sizing.reset-size8.size11,.css-63uqft .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-63uqft .katex .sizing.reset-size9.size1,.css-63uqft .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-63uqft .katex .sizing.reset-size9.size2,.css-63uqft .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-63uqft .katex .sizing.reset-size9.size3,.css-63uqft .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-63uqft .katex .sizing.reset-size9.size4,.css-63uqft .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-63uqft .katex .sizing.reset-size9.size5,.css-63uqft .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-63uqft .katex .sizing.reset-size9.size6,.css-63uqft .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-63uqft .katex .sizing.reset-size9.size7,.css-63uqft .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-63uqft .katex .sizing.reset-size9.size8,.css-63uqft .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-63uqft .katex .sizing.reset-size9.size9,.css-63uqft .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-63uqft .katex .sizing.reset-size9.size10,.css-63uqft .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-63uqft .katex .sizing.reset-size9.size11,.css-63uqft .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-63uqft .katex .sizing.reset-size10.size1,.css-63uqft .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-63uqft .katex .sizing.reset-size10.size2,.css-63uqft .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-63uqft .katex .sizing.reset-size10.size3,.css-63uqft .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-63uqft .katex .sizing.reset-size10.size4,.css-63uqft .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-63uqft .katex .sizing.reset-size10.size5,.css-63uqft .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-63uqft .katex .sizing.reset-size10.size6,.css-63uqft .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-63uqft .katex .sizing.reset-size10.size7,.css-63uqft .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-63uqft .katex .sizing.reset-size10.size8,.css-63uqft .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-63uqft .katex .sizing.reset-size10.size9,.css-63uqft .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-63uqft .katex .sizing.reset-size10.size10,.css-63uqft .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-63uqft .katex .sizing.reset-size10.size11,.css-63uqft .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-63uqft .katex .sizing.reset-size11.size1,.css-63uqft .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-63uqft .katex .sizing.reset-size11.size2,.css-63uqft .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-63uqft .katex .sizing.reset-size11.size3,.css-63uqft .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-63uqft .katex .sizing.reset-size11.size4,.css-63uqft .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-63uqft .katex .sizing.reset-size11.size5,.css-63uqft .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-63uqft .katex .sizing.reset-size11.size6,.css-63uqft .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-63uqft .katex .sizing.reset-size11.size7,.css-63uqft .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-63uqft .katex .sizing.reset-size11.size8,.css-63uqft .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-63uqft .katex .sizing.reset-size11.size9,.css-63uqft .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-63uqft .katex .sizing.reset-size11.size10,.css-63uqft .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-63uqft .katex .sizing.reset-size11.size11,.css-63uqft .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-63uqft .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-63uqft .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-63uqft .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-63uqft .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-63uqft .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-63uqft .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-63uqft .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-63uqft .katex .delimcenter{position:relative;}.css-63uqft .katex .op-symbol{position:relative;}.css-63uqft .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-63uqft .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-63uqft .katex .op-limits>.vlist-t{text-align:center;}.css-63uqft .katex .accent>.vlist-t{text-align:center;}.css-63uqft .katex .accent .accent-body{position:relative;}.css-63uqft .katex .accent .accent-body:not(.accent-full){width:0;}.css-63uqft .katex .overlay{display:block;}.css-63uqft .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-63uqft .katex .mtable .arraycolsep{display:inline-block;}.css-63uqft .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-63uqft .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-63uqft .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-63uqft .katex .svg-align{text-align:left;}.css-63uqft .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-63uqft .katex svg path{stroke:none;}.css-63uqft .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-63uqft .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-63uqft .katex .stretchy::before,.css-63uqft .katex .stretchy::after{content:'';}.css-63uqft .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-63uqft .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-63uqft .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-63uqft .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-63uqft .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-63uqft .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-63uqft .katex .x-arrow-pad{padding:0 0.5em;}.css-63uqft .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-63uqft .katex .x-arrow,.css-63uqft .katex .mover,.css-63uqft .katex .munder{text-align:center;}.css-63uqft .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-63uqft .katex .fbox,.css-63uqft .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-63uqft .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-63uqft .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-63uqft .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-63uqft .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-63uqft .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-63uqft .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-63uqft .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-63uqft .katex .mtr-glue{width:50%;}.css-63uqft .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-63uqft .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-63uqft .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-63uqft .katex-display{display:block;margin:1em 0;text-align:center;}.css-63uqft .katex-display>.katex{display:block;white-space:nowrap;}.css-63uqft .katex-display>.katex>.katex-html{display:block;position:relative;}.css-63uqft .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-63uqft .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-63uqft .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-63uqft body{counter-reset:katexEqnNo mmlEqnNo;}.css-63uqft table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-63uqft .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-63uqft .tableBlock thead,.css-63uqft .tableBlock thead th{border-bottom:1px solid #333!important;}.css-63uqft .tableBlock th,.css-63uqft .tableBlock td{padding:10px;text-align:left;}.css-63uqft .tableBlock th{font-weight:bold!important;}.css-63uqft .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-63uqft .tableBlock caption>p{margin:0;}.css-63uqft .tableBlock th>p,.css-63uqft .tableBlock td>p{margin:0;}.css-63uqft .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-63uqft .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-63uqft .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-63uqft .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-63uqft .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-63uqft .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-63uqft .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-63uqft .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-63uqft .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-63uqft .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-63uqft .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-63uqft .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-63uqft .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-63uqft .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-63uqft .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-63uqft .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-63uqft .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-63uqft .tableBlock [data-text-align='center']{text-align:center;}.css-63uqft .tableBlock [data-text-align='left']{text-align:left;}.css-63uqft .tableBlock [data-text-align='right']{text-align:right;}.css-63uqft .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-63uqft .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-63uqft .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-63uqft .tableBlock__font-size--xxsmall{font-size:10px;}.css-63uqft .tableBlock__font-size--xsmall{font-size:12px;}.css-63uqft .tableBlock__font-size--small{font-size:14px;}.css-63uqft .tableBlock__font-size--large{font-size:18px;}.css-63uqft .tableBlock__border--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-63uqft .tableBlock__border--bordered td,.css-63uqft .tableBlock__border--bordered th{border:1px solid #e2e5e7;}.css-63uqft .tableBlock__border--borderless tbody+tbody,.css-63uqft .tableBlock__border--borderless td,.css-63uqft .tableBlock__border--borderless th,.css-63uqft .tableBlock__border--borderless tr,.css-63uqft .tableBlock__border--borderless thead,.css-63uqft .tableBlock__border--borderless thead th{border:0!important;}.css-63uqft .tableBlock:not(.tableBlock__table-striped) tbody tr{background-color:unset!important;}.css-63uqft .tableBlock__table-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-63uqft .tableBlock__table-compactl th,.css-63uqft .tableBlock__table-compact td{padding:3px!important;}.css-63uqft .tableBlock__full-size{width:100%;}.css-63uqft .textBlock{margin-bottom:16px;}.css-63uqft .textBlock__text-formatting--finePrint{font-size:12px;}.css-63uqft .textBlock__text-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-63uqft .textBlock__text-infoBox p{margin:0;}.css-63uqft .textBlock__text-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-63uqft .textBlock__text-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-63uqft .textBlock__text-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-63uqft .textBlock__text-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-63uqft .textBlock__text-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-63uqft .textBlock__text-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-63uqft .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-63uqft .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-63uqft.css-63uqft{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-63uqft.css-63uqft:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-63uqft .js-external-link-button.link-like,.css-63uqft .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-63uqft .js-external-link-button.link-like:hover,.css-63uqft .js-external-link-anchor:hover,.css-63uqft .js-external-link-button.link-like:active,.css-63uqft .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-63uqft .js-external-link-button.link-like:focus-visible,.css-63uqft .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-63uqft p,.css-63uqft div{margin:0;display:block;}.css-63uqft pre{margin:0;display:block;}.css-63uqft pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-63uqft pre:not(:first-child){padding-top:8px;}.css-63uqft ul,.css-63uqft ol{display:block margin:0;padding-left:20px;}.css-63uqft ul li,.css-63uqft ol li{padding-top:8px;}.css-63uqft ul ul,.css-63uqft ol ul,.css-63uqft ul ol,.css-63uqft ol ol{padding-top:0;}.css-63uqft ul:not(:first-child),.css-63uqft ol:not(:first-child){padding-top:4px;} Interpretation

Significance level α

P Value Calculator from T Score

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

For a one-sample or paired t-test, df = N – 1. For an independent samples t-test, df = (N₁ – 1) + (N₂ – 1), where N is the sample size.

T test calculator

Apa results generator, further information.

• p-values and statistical significance
• confidence intervals

What does the t-test tell you?

When to use t-test vs anova, what is the difference between a t-test and a z-test, when to use t-test vs chi-square.