what is representation theory

Representation Theory

Representation theory is fundamental in the study of objects with symmetry. 

It arises in contexts as diverse as card shuffling and quantum mechanics. An early success was the work of Schur and Weyl, who computed the representation theory of the symmetric and unitary groups; the answer is closely related to the classical theory of symmetric functions and deeper study leads to intricate questions in combinatorics.

More recently, methods from geometry and topology have greatly enhanced our understanding of these questions (“geometric representation theory”). The study of affine Lie algebras and quantum groups has brought many new ideas and viewpoints, and representation theory now furnishes a basic language for other fields, including the modern theory of automorphic forms.

All of these aspects are studied by Stanford faculty.  Topics of recent seminars include combinatorial representation theory as well as quantum groups.

Ahoy! This page uses MathJax to typeset math symbols. If you’re seeing code rather than nice, typeset symbols, you may need to hit “refresh” to render things cleanly.

Applied Representation Theory : 000

What is Representation Theory?

We present an overview of what representation theory is, together we a few examples of group representations. 

What's inside:

The definition of representations and their modules

An introduction to groups

Basic examples of group representations

Representations

Mathematically, a representation is a map between two kinds of objects. Schematically, it is given by $\pi$:

\begin{equation}\label{schematic}\pi : \mathcal{A} \rightarrow \mathcal{M}.\end{equation}

Here $\mathcal{A}$ is some kind of algebraic object, like a group or an a algebra, and $\mathcal{M}$ is a set of objects upon which $\mathcal{A}$ acts. That action is encoded by the mapping $\pi$, which is called the representation of $\mathcal{A}$ on $\mathcal{M}$.

For most practical purposes relevant to this course, $\mathcal{M}$ is a vector space. More precisely, it is a vector space of linear endomorphisms of some other vector space $V$:

$$\mathsf{End}(V) = \left\{ f \;\Big|\; f : V\rightarrow V,\; f\mathrm{\,is\,linear}\right\}.$$

In this context, the vector space $V$ is often referred to as an $\mathcal{A}$ -module . Sometimes we call such endomorphisms operators .

By the way, any map $f$ between any two vector spaces $V$ and $W$

$$f: V\rightarrow W$$

is linear if it compatible with scalar multiplication and vector addition:

$$f(a\overrightarrow{x} + b\overrightarrow{y}) = af(\overrightarrow{x}) + bf(\overrightarrow{y}).$$

For a concrete example, let $V$ be the $n$-dimensional, Euclidean vector space $\mathbb{R}^{n}$. Then $\mathsf{End}(\mathbb{R}^{n})$ is the space of $n\times n$-matrices:

$$\mathsf{End}(\mathbb{R}^{n}) = \mathsf{Hom}_{n,n}\mathbb{R}.$$

Similarly, we can consider complex representations in $\mathsf{End}(\mathbb{C}^{n})$.

The clarity afforded by such straightforward, concrete constructions can sometimes obscure the underlying structure of \eqref{schematic}. The group of matrices - which we're calling $\mathcal{A}$ - just also happens to be a subset of the endomorphisms of $\mathbb{R}^{n}$ or $\mathbb{C}^{n}$. This is because we often define matrix Lie groups or algebras as subsets of $\mathsf{Hom}_{n,n}\mathbb{R}$ or $\mathsf{Hom}_{n,n}\mathbb{C}$. Familiar examples include the orthogonal matrices $^{1}$:

$$\mathsf{O}(n) = \left\{ M \in \mathsf{Hom}_{n,n}\mathbb{R} \;\Big|\; M^{-1} = M^{\sf T}\right\},$$

and the unitary matrices

$$\mathsf{U}(n) = \left\{ M \in \mathsf{Hom}_{n,n}\mathbb{C} \;\Big|\; M^{-1} = M^{\dagger}\right\}.$$

The former typically represent the isometries of $\mathbb{R}^{n}$ - i.e. rotations and reversals, whereas the latter are familiar from the study of operators in quantum mechanics. 

Things can get truly sticky if we consider the general linear group , 

$$\mathsf{GL}_{n}\mathbb{R} = \left\{ M \in \mathsf{Hom}_{n,n}\mathbb{R} \;\Big | \; \det M \neq 0\right\},$$

which captures almost all of $\mathsf{End}(\mathbb{R}^{n})$.

Nevertheless, groups like $\mathsf{O}(n)$ and $\mathsf{U}(n)$ are algebraic objects in their own right, and will each have an infinite tower of distinct modules upon which they can be represented. The study and classification of such modules is primary aim of representation theory.

Group Representations

No doubt you have some passing familiarity with groups - its hard to study symmetries in physics without some. Many a physicist develops their algebraic sophistication through the study of representation theory, particularly that of matrix Lie groups. As such, we'll briefly recount the details here.

A group is a set $G$ together with a binary operation:

$$\star : G\times G \rightarrow G,$$

that is subject to three requirements. First, there is an identity element in $G$, say $1$, such that for all $g$ in $G$,

$$1\star g = g\star 1 = g.$$

Relatedly, every $g$ in $G$ much have an associated inverse $g^{-1}$, such that

$$g\star g^{-1} = g^{-1}\star g = 1.$$

Finally, the operation $\star$ is associative , which means that for all $f,g,h$ in $G$

$$(f\star g)\star h = f\star(g\star h) = f\star g \star h.$$

Essentially, associativity means that the product of group elements

$$f\star g \star h \star \dots$$

is independent of the order of evaluation. In particular, its uniquely defined.

Quintessential examples of groups include the integers ($\mathbb{Z}$) with addition, or the real $(\mathbb{R})$ and complex $(\mathbb{C})$ numbers with either addition or multiplication$^{2}$ 

or even the rational numbers :

$$\mathbb{Q} = \left\{ \frac{a}{b} \;\Big|\; a,b \in \mathbb{Z}\right\}.$$

We will now consider a few examples of groups and their associated representations.

Finite Group Representations

Consider the cyclic groups :

$$\mathbb{Z}_{n} = \left\{ q\; \mathrm{mod} \;n \;\Big|\;q \in \mathbb{Z}\right\},$$

where $n$ is a positive number. Here $q$ mod or “modulo” $n$ means the remainder of the fraction $q/n$.

Any complex vector space $V$ can be a module for $\mathbb{Z}_{n}$, where the representation of $\mathbb{Z}_{n}$ is furnished by the set of scalars 

$$ \{ \pi_{q} = e^{2\pi i q/n} \;\Big|\; q \in \mathbb{Z}_{n}\}.$$

Here the scalars $\pi_{q}$ act as linear operators on $V$.

A notable example that we will see a lot of is $\mathbb{Z}_{2} = \left\{\pm 1\right\}$. Notice that any real vector space can also serve as a module for $\mathbb{Z}_{2}$.

Abelian Group Representations

Abelian groups are those whose group operation is commutative. Often we refer to it as addition and use the associated notation, $a + b.$

In this context the unit element is typically written as $0$ and inverse elements $a^{-1}$ are often written as  $-a$.

A typical example that is also a generalization of the cyclic groups above is the group $\mathsf{U}(1)$:

$$\mathsf{U}(1) = \left\{ \pi_{\theta} = e^{i \theta} \;\Big|\; 0 \leq \theta < 2\pi \right\},$$

which also can be thought of as the unit circle

$$\mathsf{U}(1) = S^{1} =  \left\{ z \in \mathbb{C} \;\Big|\; |z|^{2} = 1\right\}.$$

Again, any complex vector space $V$ can serve as a module for $\mathsf{U}(1)$, where the representation again acts by scalar multiplication.

Lie Group Representations

Notice that the group $\mathsf{U}(1)$ can be represented by a manifold, $S^{1}$. That is, the group has a geometric interpretation as well. For historical reasons, such continuous groups are typically called Lie groups , and as we will see in this course, their geometric nature helps elucidate their structure as a group.

A simple example of a nonabeliean Lie group is $\mathsf{SU}(2)$, the isometries of $\mathbb{C}^{2}$ that have determinant 1. These are often used to discuss spin-$\frac{1}{2}$ physics, where the spin doublet in $\mathbb{C}^{2}$ is understood to be a module for the action of $\mathsf{SU}(2)$. The representation is then given in terms of the physicists ' $\sigma$ -matrices :

$$\pi_{\alpha} =e^{2\pi i \alpha \cdot \sigma},$$

$$\sigma_{1} = \left(\begin{array}{cc} 0 & 1 \\ 1 & 0\end{array}\right),\quad \sigma_{2} = \left(\begin{array}{rr} 0 & -i \\ i & 0\end{array}\right),\quad \sigma_{3} = \left(\begin{array}{rr} 1& 0 \\ 0 & -1\end{array}\right),$$

and $\alpha$, roughly, can be thought of as a vector in $\mathbb{R}^{3}$. More precisely, $\alpha$ parametrizes the three-sphere $S^{3}$, which for smaller values of $\alpha$ behaves just like $\mathbb{R}^{3}$. It is this sort of relationship: looking in a neighborhood of small parameter values for Lie groups - that allows a clear understanding of their structure.

the exponential map

a relationship between endomorphisms and the general linear group

the definition of an algebra

Further Reading

While popular with physicists, Howard Georgi's book Lie Algebras in Particle Physics is a disorderly mess, and so may be hard to read. Nevertheless, it has many examples familiar from physics. From a mathematical point of view, a reasonable text with a lot of problems is Hungerford's Algebra .

Given a vector space $V$, prove that $\mathsf{End}(V)$ is also a vector space. Look up the definition if needed.

Find a representation of $\mathbb{Z}_{n}$ on $\mathbb{R}^{2}$. Generalize this to a representation of $\mathsf{U}(1)$. What is the relation of this to group $\mathsf{SO}(2)$, that subset of $\mathsf{O}(2)$ with unit determinant?

Verify that $\mathsf{SU}(2)$ is parametrized by $S^{3}$ by using the defining constraint that $M^{\dagger} = M^{-1}$, for all $M$ in $\mathsf{SU}(2)$. (Hint: parametrize the group by two complex numbers that share a single constraint.) 

Argue that the subset of the unitary matrices of dimension $n$ that have unit determinant are also groups. These are the special unitary groups , $\mathsf{SU}(n)$. Repeat that argument to define the special orthogonal groups , $\mathsf{SO}(n)$.

For the physicists' $\sigma$ matrices above, the identity:

$$e^{2\pi i \alpha \cdot \sigma} = \cos(2\pi|\alpha|) \mathbb{1}+ \sin(2\pi|\alpha|) \alpha\cdot\sigma,$$

where $|\alpha|$ is the modulus of the three-dimensional, real vector $\alpha$, and $\mathbb{1}$ is the identity matrix.

$^{1}$: We can of course consider orthogonal matrices of complex numbers, but for practical application we usually restrict to the reals.

$^{2}$: This is not strictly true for multiplication. There’s a small caveat. We’ll start with that caveat next time.

©2021 The Pasayten Institute cc by-sa-4.0

Lecture 1 : The Exponential Map

• Tools and Resources
• Customer Services
• Affective Science
• Biological Foundations of Psychology
• Clinical Psychology: Disorders and Therapies
• Cognitive Psychology/Neuroscience
• Developmental Psychology
• Educational/School Psychology
• Forensic Psychology
• Health Psychology
• History and Systems of Psychology
• Individual Differences
• Methods and Approaches in Psychology
• Neuropsychology
• Organizational and Institutional Psychology
• Personality
• Psychology and Other Disciplines
• Social Psychology
• Sports Psychology
• Share This Facebook LinkedIn Twitter

Article contents

Social representation theory: an historical outline.

• Wolfgang Wagner Wolfgang Wagner Institute of Psychology, University of Tartu, Estonia
• https://doi.org/10.1093/acrefore/9780190236557.013.606
• Published online: 30 July 2020

The concept of social representation (SR) was developed by Serge Moscovici in 1961 as a social psychological approach articulating individual thinking and feeling with collective interaction and communication. SRs are conceived as symbolic forms that come about through interpersonal and media communication. They are the ways individuals think, interact with others, and shape social objects in their interaction with the local world.

This text presents an outline of the history of social representation theory (SRT), using a four-period model: first, creation and incubation in France starting with Moscovici’s first book; second, the opening to the English-speaking academe around 1980; third, institutionalization and proliferation with the start of the journal papers on SRs and regular conferences in 1992; and, fourth, normalization, approximately from 2000 onwards.

The first period (1961–1984) started with Serge Moscovici’s first presentation of his ideas in a French-language volume on “La psychanalyse son image et son public.” This was republished in an updated version in 1976 and translated into English in 2008. The theory postulates cognitive and social factors in the genesis and structure of SRs. These are accompanied by specific styles of communication that reflect the communicators’ identity and ideology. Together these aspects constitute common sense.

The first period was a time of incubation because Moscovici and his first PhD students, Claudine Herzlich, Denise Jodelet, and Jean-Claude Abric, tried the concept in different domains. The second half of this period saw Moscovici and collaborators extend SRT’s theoretical frame to include the idea of consensual vs. reified domains. A consensual domain of communication is characterized by the free interchange of attitudes and opinions, while a reified domain is determined by institutionalized rules. Moscovici also postulated a process of cognitive polyphasia. By cognitive polyphasia he described a phenomenon where individuals use different and even contradictory thoughts about the same issue depending on the social setting they are in.

The year 1984 marked the publication of a book for English-speaking scholars edited by Robert Farr and Moscovici that collected papers from an international conference in 1979. It was the first book-length collection of works on SRT and highlighted empirical research by a variety of international scholars. The period following 1979 through to 1992 saw a broadening of the base of scholars becoming interested in SRT. The 1980s brought Willem Doise’s conceptualizing of anchoring as a process of social marking, Abric’s theory of core and peripheral elements of a representation, and Hilde Himmelweit’s founding of a societal psychology.

Proliferation was boosted 1992 by the founding of the journal Papers on Social Representations and the beginning of a biannual series of International Conferences on Social Representations, starting in 1992. This increased the international visibility of SRT and helped scholars to organize themselves around topics and form cross-national research groups.

The period from 1992 to the first decade of the new century was characterized by an increasing number of empirical and theoretical studies. A series of theoretical branches emerged: there was research on the micro-genesis of SRs on the individual level, an extension of the structural theory of SRs, the discussion of the socially constructive aspects and sociopolitical uses of SRT, the design of a dialogical approach to the mind and social life, and Moscovici’s suggestion to consider large-scale themata as a factor in social thinking.

If the period after 1992 was a time of institutionalization, the time after the turn of the century can be called a period of normalization. That is, a period when SRT was presented in chapters for handbooks of social psychology and when dedicated handbooks and monographs were published. From this period onward it becomes virtually impossible to give even a superficial account of the most important contributions to SRT’s burgeoning field of research and theory development.

• social sciences
• social psychology
• history of psychology
• social representations
• social construction

You do not currently have access to this article

Please login to access the full content.

Access to the full content requires a subscription

Printed from Oxford Research Encyclopedias, Psychology. Under the terms of the licence agreement, an individual user may print out a single article for personal use (for details see Privacy Policy and Legal Notice).

date: 12 June 2024

• Cookie Policy
• Privacy Policy
• Legal Notice
• Accessibility
• [162.248.224.4]
• 162.248.224.4

Character limit 500 /500

Stack Exchange Network

Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

Q&A for work

Connect and share knowledge within a single location that is structured and easy to search.

Importance of Representation Theory

Representation theory is a subject I want to like (it can be fun finding the representations of a group), but it's hard for me to see it as a subject that arises naturally or why it is important. I can think of two mathematical reasons for studying it:

The character table of a group is packs a lot of information about the group and is concise.

It is practically/computationally nice to have explicit matrices that model a group.

But there must certainly be deeper things that I am missing. I can understand why one would want to study group actions (the axioms for a group beg you to think of elements as operators), but why look at group actions on vector spaces? Is it because linear algebra is so easy/well-known (when compared to just modules, say)?

I am also told that representation theory is important in quantum mechanics. For example, physics should be $\mathrm{SO}(3)$ invariant and when we represent this on a Hilbert space of wave-functions, we are led to information about angular momentum. But this seems to only trivially invoke representation theory since we already start with a subgroup of $\mathrm{GL}(n)$ and then extend it to act on wave functions by $\psi(x,t) \mapsto \psi(Ax,t)$ for $A$ in $\mathrm{SO}(n)$ .

This Wikipedia article on particle physics and representation theory claims that if our physical system has $G$ as a symmetry group, then there is a correspondence between particles and representations of $G$ . I'm not sure if I understand this correspondence since it seems to be saying that if we act an element of G on a state that corresponds to some particle, then this new state also corresponds to the same particle. So a particle is an orbit of the $G$ action? Anyone know of good sources that talk about this?

• representation-theory

• 88 $\begingroup$ Much of math is reducing hard things to linear algebra. For examples: calculus (differentiating is locally replacing your function by the best linear function available), representation theory, homology. $\endgroup$ –  Noah Snyder Jul 24, 2010 at 13:01
• $\begingroup$ uregina.ca/~mareal/flag-coh.pdf // yufeizhao.com/papers/youngtab-hcmr.pdf // math.ku.edu/~jmartin/courses/math824-F10 // projecteuclid.org/euclid.lnms/1215467407 just a couple pointers to representation theory that may be interesting. Not physical though. $\endgroup$ –  isomorphismes Apr 7, 2017 at 4:18
• $\begingroup$ Obviously, this is a fascinating but really challenging theory. It seems that this thread demands xk+ reputations to even read. But sincere thanks to those who give fundamental explanation! $\endgroup$ –  MathArt Mar 26 at 8:19

9 Answers 9

One comment about your sentence "this seems to only trivially invoke representation theory". It might be surprising, but such obvious representations are actually the source of interesting mathematics, and a lot of effort of representation theorists is devoted to studying them.

More precisely: start with a group (in your example $SO(n)$ ) acting on a space $X$ (in your example $\mathbb R^n$ ), and look at the space of functions on $X$ (let me write it $\mathcal F(X)$ ; in a careful treatment, one would have to think about whether we wanted continuous, smooth, $L^2$ , or some other kind of functions, but I will suppress that kind of technical consideration).

Then, as you observe, there is a natural representation of $G$ on $\mathcal F(X)$ .

You are right that from a certain point of view this seems trivial, because the representation is obvious. Unlike when one first learns rep'n theory of finite groups, where one devotes a lot of effort to constructing reps., in this context, the rep. stares you in the face.

So how can this be interesting?

Well, the representation $\mathcal F(X)$ will almost never be irreducible. How does this representation decompose?

Suddenly we are looking at a hard representation theoretic problem.

First, we have to work out the list of irreps of $G$ (which is much like what one does in a first course on rep'n theory of finite groups).

Second, we have to figure out how $\mathcal F(X)$ decomposes, which involves representation theory (among other things, you have to develop methods for investigating this sort of question), and also often a lot of analysis (because typically $\mathcal F(X)$ will be infinite dimensional, and may be a Hilbert space, or have some other similar sort of topological vector space structure which should be incorporated into the picture).

I don't think I should say too much more here, but I will just give some illustrative examples:

If $ X = G = S^1$ (the circle group, say thought of as $\mathbb R/\mathbb Z$ ) acting on itself by addition, then the solution to the problem of decomposing $\mathcal F(S^1)$ is the theory of Fourier series. (Note that a function on $S^1$ is the same as a periodic function on $\mathbb R$ .)

If $ X = G = \mathbb R$ , with $G$ acting on itself by addition, then the solution to the above question (how does $\mathcal F(\mathbb R)$ decompose under the action of $\mathbb R$ ) is the theory of the Fourier transform.

If $ X = S^2$ and $G = SO(3)$ acting on $X$ via rotations, then decomposing $\mathcal F(S^2)$ into irreducible representations gives the theory of spherical harmonics. (This is an important example in quantum mechanics; it comes up for example in the theory of the hydrogen atom, when one has a spherical symmetry because the electron orbits the nucleus, which one thinks of as the centre of the sphere.)

If $ X = SL_2(\mathbb R)/SL_2(\mathbb Z)$ (this is the quotient of a Lie group by a discrete subgroup, so is naturally a manifold, in this case of dimension 3), with $G = SL_2(\mathbb R)$ acting by left multiplication, then the problem of decomposing $\mathcal F(X)$ leads to the theory of modular forms and Maass forms, and is the first example in the more general theory of automorphic forms.

Added: Looking over the other answers, I see that this is an elaboration on AD.'s answer.

Groups very, very rarely appear abstractly in (mathematical) nature : when we encounter them, it is almost always in the form of a representation (a linear representation, a permutation representation, a non-linear representation in the form of automorphisms of an algebra, of a variety, of a manifold, of a group (!)).

It is thus only natural that the study of representation theory be important! I would go further, turn your question backwards, and claim that group theory is important because it allows us to study the representations of groups.

The representation theory of finite groups can be used to prove results about finite groups themselves that are otherwise much harder to prove by "elementary" means. For instance, the proof of Burnside's theorem (that a group of order $p^a q^b$ is solvable). A lot of the classification proof of finite simple groups relies on representation theory (or so I'm told, I haven't read the proof...).

Mathematical physics. Lie algebras and Lie groups definitely come up here, but I'm not familiar enough to explain anything. In addition, the classification of complex simple Lie algebras relies on the root space decomposition, which is a significant (and nontrivial) fact about the representation theory of semisimple Lie algebras.

Number theory. The nonabelian version of L-functions (Artin L-functions) rely on the representations of the Galois group (in the abelian case, these just correspond to sums of 1-dimensional characters). For instance, the proof that Artin L-functions are meromorphic in the whole plane relies on (I think) Artin Brauer's theorem (i.e., a corollary of the usual statement) that any irreducible character is an rational integer combination of induced characters from cyclic subgroups -- this is in Serre's Linear Representations of Finite Groups. Also, the Langlands program studies representations of groups $GL_n(\mathbb{A}_K)$ for $\mathbb{A}_K$ the adele ring of a global field. This is a generalization of standard "abelian" class field theory (when $n=1$ and one is determining the character group of the ideles).

Combinatorics. The representation theory of the symmetric group has a lot of connections to combinatorics, because you can parametrize the irreducibles explicitly (via Young diagrams), and this leads to the problem of determining how these Young diagrams interact. For instance, what does the tensor product of two Young diagrams look like when decomposed as a sum of Young diagrams? What is the dimension of the irreducible representation associated to a Young diagram? These problems have a combinatorial flavor.

I should add the disclaimer that I have not formally studied representation theory, and these are likely to be an unrepresentative sample of topics (some of which I have only vaguely heard about).

• 2 $\begingroup$ An interesting note on the classification of finite simple groups. Just a sentence to get you going: "A rough count by Gorenstein [in the early 80's] showed that the original proof of the Classification Theorem occupies about 15,000 journal pages." $\endgroup$ –  Tom Stephens Jul 24, 2010 at 3:49
• 2 $\begingroup$ For meromorphicity of Artin L-functions, is Artin's result enough? (People normally quote Brauer's theorem in this context.) Also, I wouldn't say "Much more importantly"; after all, one of Langlands motivations in developing his program was to establish a route to proving the Artin conjecture (to the effect that the meromorphic continuation is in fact holomorphic). $\endgroup$ –  Matt E Aug 18, 2010 at 7:52

Particles correspond to specific vectors in a representation, not to $G$ -orbits! The reason has to do with "symmetry breaking." The $8$ particles in the meson octet correspond to a basis of a certain $8$ -dimensional representation of the group $\mathrm{SU}(3)$ called the "adjoint representation." At high enough energies these particles would be indistinguishable. But at low energies the " $\mathrm{SU}(3)$ symmetry has been broken" and the particles become distinguishable.

Another good physics example that's easier to understand is that the orbital states of electrons in atoms correspond to representations of the group $\mathrm{SO}(3)$ of symmetries of space (well, really $\mathrm{SU}(2)$ if you want to incorporate spin). Try reading a standard quantum mechanics textbook for a little bit of this picture and then try thinking about it in terms of representation theory.

• 5 $\begingroup$ Ah ok...so in your first example, the 8 particles correspond to a basis of the Lie algebra su(3). The physical interpretation that the adjoint action of SU(3) is irreducible is that these particles are indistinguishable at high energies? Does the symmetry breaking at low energies manifest itself mathematically somehow? More generally, every irrep of SU(3) corresponds to some group of particles? To which irrep of SU(3) does the baryon decuplet correspond? $\endgroup$ –  Eric O. Korman Jul 24, 2010 at 14:09
• 5 $\begingroup$ baryon decuplet corresponds to Sym^2(V) where V is the standard representation. That is it corresponds to the representation with highest weight (2,0). $\endgroup$ –  Noah Snyder Jul 25, 2010 at 9:03
• 1 $\begingroup$ Your first paragraph assumes that G is a broken symmetry. I don't know why you made that assumption. It was not part of the original question as far as I can tell. For example, perhaps G is the Poincare group. $\endgroup$ –  Steve Byrnes Dec 21, 2016 at 0:12

Representation theory plays a big role in the group-theoretic approach to special functions. For example, Willard Miller showed that the powerful Infeld-Hull factorization / ladder method - widely exploited by physicists - is equivalent to the representation theory of four local Lie groups. This lie-theoretic approach served to powerfully unify and "explain" all prior similar attempts to provide a unfied theory of such classes of special functions, e.g. Truesdell's influential book An Essay Toward a Unified Theory of Special Functions . Below is the first paragraph of the introduction to Willard Miller's classic monograph Lie theory and special functions

This monograph is the result of an attempt to understand the role played by special function theory in the formalism of mathematical physics. It demonstrates explicitly that special functions which arise in the study of mathematical models of physical phenomena and the identities which these functions obey are in many cases dictated by symmetry groups admitted by the models. In particular it will be shown that the factorization method, a powerful tool for computing eigenvalues and recurrence relations for solutions of second order ordinary differential equations (Infeld and Hull), is equivalent to the representation theory of four local Lie groups. A detailed study of these four groups and their Lie algebras leads to a unified treatment of a significant proportion of special function theory, especially that part of the theory which is most useful in mathematical physics.

See also Miller's sequel Symmetry and Separation of Variables . Again I quote from the preface:

This book is concerned with the relationship between symmetries of a linear second-order partial differential equation of mathematical physics, the coordinate systems in which the equation admits solutions via separation of variables, and the properties of the special functions that arise in this manner. It is an introduction intended for anyone with experience in partial differential equations, special functions, or Lie group theory, such as group theorists, applied mathematicians, theoretical physicists and chemists, and electrical engineers. We will exhibit some modern group-theoretic twists in the ancient method of separation of variables that can be used to provide a foundation for much of special function theory. In particular, we will show explicitly that all special functions that arise via separation of variables in the equations of mathematical physics can be studied using group theory. These include the functions of Lame, Ince, Mathieu, and others, as well as those of hypergeometric type. This is a very critical time in the history of group-theoretic methods in special function theory. The basic relations between Lie groups, special functions, and the method of separation of variables have recently been clarified. One can now construct a group-theoretic machine that, when applied to a given differential equation of mathematical physics, describes in a rational manner the possible coordinate systems in which the equation admits solutions via separation of variables and the various expansion theorems relating the separable (special function) solutions in distinct coordinate systems. Indeed for the most important linear equations, the separated solutions are characterized as common eigenfunctions of sets of second-order commuting elements in the universal enveloping algebra of the Lie symmetry algebra corresponding to the equation. The problem of expanding one set of separable solutions in terms of another reduces to a problem in the representation theory of the Lie symmetry algebra.

See Koornwinder's review of this book for a very nice concise introduction to the group-theoretic approach to separation of variables.

The idea of considering the representations of a group $G$ as a group of linear operators to ultimately gain informations on the group $G$ itself is an important istance of the general process of "linearization" that is employed systematically in many areas of mathematics.

In down-to-earth (and possibly vague) terms, I would say that the only general class of problems that we are able to resolve fully are those which are linear, meaning that involve only vector spaces--best if finitely dimensional :-) --and linear maps between them. When we deal with objects that are intrinsically non-linear, a widespread strategy is to try to attach to them some linear "gadgets" that in some way preserve, in a different form, some of the structure of the original object.

Two basic examples that should be well-known to every math student:

The construction of the tensor product reduces multilinear algebra to linear algebra.

The construction of the homotopy and (co)homology groups of a topological space is an attempt to "understand topology via groups and linear spaces".

The linear representations of a group $G$ respond to the same principle: they are a "linear" set of data attached to $G$ which hopefully can serve to characterize $G$.

Representation theory is one of the keys to the Fourier transform on groups (and co-set spaces etc.). For this matter, I recommend this book: Unitary representations and harmonic analysis: an introduction By Mitsuo Sugiura

If you take a look at the Wikipedia page about representation theory, you will find several applications.

Certainly, group actions used to model dynamical systems, for instance, Markov Chains, find extremely handy the results from representation theory. For example, suppose you have a deck of cards, and every time you choose two cards at random and transpose them. How long you have to wait for the deck to be randomized? The (exact) answer to this question lies exclusively in the area of representation theory! See for example the book Harmonic Analysis on Finite Groups by Ceccherini-Silberstein, Scarabotti, and Tolli.

Although many years later, for the sake of completeness -regarding the last question on references about uses in physics- i believe one might find lots of interest on the classic text by J. Baez and J. Huerta:

The Algebra of Grand Unified Theories

Lots of the mathematical physics developed during the last decades of the 20th century is reviewed there, in a particularly didactic way.

You must log in to answer this question.

Not the answer you're looking for browse other questions tagged representation-theory physics ., hot network questions.

• Can this flying island survive a 15kt nuke? (and if yes, how much more can it take?)
• Cut out rotated rectangle shape
• Why isn't "meanwhile" advisable in this sentence? Doesn't it mean "at the same time"?
• Smallest Harmonic number greater than N
• Story about a future gang initiation - but there's a twist
• is_decimal Function Implementation in C++
• Thought experiment regarding gravity
• Why are we abbreviating Player's Handbook to PHB?
• What happens when you target a dead creature with Scrying?
• How to negotiate such toxic competitiveness during my master’s studies?
• How big can a chicken get?
• Should I remove young tomato's first flowers?
• How do I emphasize a sentence without making it seem like the character is shouting?
• Executable files with a bytecode compiler/interpreter
• Password protect directory listing only and not the files themselves
• Force Mathematica to simplify a function to avoid infinities
• Reproducing Ómar Rayo's "Fresh Fog" Painting
• Ubuntu Terminal with alternating colours for each line
• PolynomialQ behaviour
• Should I ask for authorship or ignore?
• Is there a matrix with rational entries similar to a given matrix?
• What rights do I have to improve upon patented inventions?
• Are usb-c through hole shell stakes connected to GND or are they just there for fastening purposes only?
• Found possible instance of plagiarism in joint review paper and PhD thesis of high profile collaborator, what to do?

Search form

• Travel & Maps
• Our Building
• Supporting Mathematics
• Art and Oxford Mathematics
• Equality, Diversity & Inclusion
• Undergraduate Study
• Postgraduate Study
• Current Students
• Research Groups
• Case Studies
• Faculty Books
• Oxford Mathematics Alphabet
• Oxford Online Maths Club
• Oxford Maths Festival 2023
• It All Adds Up
• Problem Solving Matters
• PROMYS Europe
• Oxfordshire Maths Masterclasses
• Outreach Information
• Mailing List
• Key Contacts
• People List
• A Global Department
• Research Fellowship Programmes
• Professional Services Teams
• Conference Facilities
• Public Lectures & Events
• Departmental Seminars & Events
• Special Lectures
• Conferences
• Summer Schools
• Past Events
• Alumni Newsletters
• Info for Event Organisers & Attendees

What is Representation Theory and how is it used? Oxford Mathematics Research investigates

Oxford Mathematician Karin Erdmann  specializes in the areas of algebra known as representation theory (especially modular representation theory) and homological algebra (especially Hochschild cohomology). Here she discusses her latest work.

"Roughly speaking, representation theory investigates how algebraic systems can act on vector spaces. When the vector spaces are finite-dimensional this allows one to explicitly express the elements of the algebraic system by matrices, hence one can exploit linear algebra to study 'abstract' algebraic systems. In this way one can study symmetry, via group actions. One can also study irreversible processes. Algebras and their representations provide a natural frame for this.

An algebra is a ring which also is a vector space such that scalars commute with everything. An important construction are path algebras: Take a directed graph $Q$, which we call a quiver, and take a coefficient field $K$. Then the path algebra $KQ$ is the vector space over $K$ with basis all paths in $Q$. This becomes an algebra, where the product of two basis elements is either its concatenation if this exists, or is zero otherwise.

Algebras generalize groups, namely if we start with a group, we get naturally an algebra: take the vector space with basis labelled by the group, and extend the group multiplication to a ring structure.

When the coefficients are contained in the complex numbers, representations of groups have been studied for a long time, and have many applications. With coefficients in the integers modulo $2$, for example, the algebras and their representations are much harder to understand. For some groups, the representations have 'finite type'. These are well-understood but almost always they have 'infinite type'. With a few exceptional 'tame' cases, these are usually 'wild', that is there is no hope of a classification of the representations.

The same cases occur precisely for modulo 2 arithmetic and when the symmetry is based on dihedral or semidihedral or quaternion 2-groups. Dihedral 2-groups are symmetries of regular $n$-gons when $n$ is a power of 2. The smallest quaternion group is the famous one discovered by Hamilton.

Viewing these symmetries from groups in the wider context of algebras was used (a while ago) to classify such tame situations. Recently it was discovered that this is part of a much larger universe. Namely one can construct algebras from surface triangulations, in which the ones from the group setting occur as special cases.

One starts with a surface triangulation, and constructs from this a quiver, that is, a directed graph: Replace each edge of the triangulation by a vertex, and for each triangle

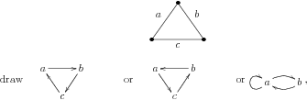
where in the last case $a=c\neq b$. At any boundary edge, draw a loop.

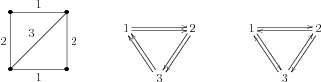
For example, consider triangulation of the torus with two triangles, as shown below. Then there are, up to labelling, two possible orientations of triangles and two possible quivers:

The tetrahedral triangulation of the sphere

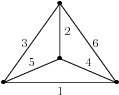
gives rise to several quivers, depending on the orientation of each triangle, for example:

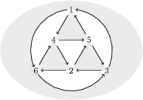
The crystal in the north wing of the Andrew Wiles Building, home of Oxford Mathematics (image drawn above) can be viewed as a triangulation of a surface with boundary. We leave drawing the quiver to the reader.

Starting with the path algebra of such a quiver, we construct algebras by imposing explicit relations, which mimic the triangulation. Although the quiver can be arbitrarily large and complicated, there is an easy description of the algebras. We call these 'weighted surface algebras.' This is joint work with A. Skowronski .

We show that these algebras place group representations in a wider context. The starting point is that (with one exception) the cohomology of a weighted surface algebra is periodic of period four, which means that these algebras generalize group algebras with quaternion symmetry.

The relations which mimic triangles can be degenerated, so that the product of two arrows around a triangle become zero in the algebra. This gives rise to many new algebras. When all such relations are degenerated, the resulting algebras are very similar to group algebras with dihedral symmetry. If we degenerate relations around some but not all triangles, we obtain algebras which share properties of group algebras with semidihedral symmetry. Work on these is in progress."

• Table of Contents
• Random Entry
• Chronological
• Editorial Information
• About the SEP
• Editorial Board
• How to Cite the SEP
• Special Characters
• Advanced Tools
• Support the SEP
• PDFs for SEP Friends
• Make a Donation
• SEPIA for Libraries
• Entry Contents

Bibliography

Academic tools.

• Friends PDF Preview
• Author and Citation Info
• Back to Top

Political Representation

The concept of political representation is misleadingly simple: everyone seems to know what it is, yet few can agree on any particular definition. In fact, there is an extensive literature that offers many different definitions of this elusive concept. [Classic treatments of the concept of political representations within this literature include Pennock and Chapman 1968; Pitkin, 1967 and Schwartz, 1988.] Hanna Pitkin (1967) provides, perhaps, one of the most straightforward definitions: to represent is simply to “make present again.” On this definition, political representation is the activity of making citizens’ voices, opinions, and perspectives “present” in public policy making processes. Political representation occurs when political actors speak, advocate, symbolize, and act on the behalf of others in the political arena. In short, political representation is a kind of political assistance. This seemingly straightforward definition, however, is not adequate as it stands. For it leaves the concept of political representation underspecified. Indeed, as we will see, the concept of political representation has multiple and competing dimensions: our common understanding of political representation is one that contains different, and conflicting, conceptions of how political representatives should represent and so holds representatives to standards that are mutually incompatible. In leaving these dimensions underspecified, this definition fails to capture this paradoxical character of the concept.

This encyclopedia entry has three main goals. The first is to provide a general overview of the meaning of political representation, identifying the key components of this concept. The second is to highlight several important advances that have been made by the contemporary literature on political representation. These advances point to new forms of political representation, ones that are not limited to the relationship between formal representatives and their constituents. The third goal is to reveal several persistent problems with theories of political representation and thereby to propose some future areas of research.

1.1 Delegate vs. Trustee

1.2 pitkin’s four views of representation, 2. changing political realities and changing concepts of political representation, 3. contemporary advances, 4. future areas of study, a. general discussions of representation, b. arguments against representation, c. non-electoral forms of representation, d. representation and electoral design, e. representation and accountability, f. descriptive representation, other internet resources, related entries, 1. key components of political representation.

Political representation, on almost any account, will exhibit the following five components:

• some party that is representing (the representative, an organization, movement, state agency, etc.);
• some party that is being represented (the constituents, the clients, etc.);
• something that is being represented (opinions, perspectives, interests, discourses, etc.); and
• a setting within which the activity of representation is taking place (the political context).
• something that is being left out (the opinions, interests, and perspectives not voiced).

Theories of political representation often begin by specifying the terms for the first four components. For instance, democratic theorists often limit the types of representatives being discussed to formal representatives — that is, to representatives who hold elected offices. One reason that the concept of representation remains elusive is that theories of representation often apply only to particular kinds of political actors within a particular context. How individuals represent an electoral district is treated as distinct from how social movements, judicial bodies, or informal organizations represent. Consequently, it is unclear how different forms of representation relate to each other. Andrew Rehfeld (2006) has offered a general theory of representation which simply identifies representation by reference to a relevant audience accepting a person as its representative. One consequence of Rehfeld’s general approach to representation is that it allows for undemocratic cases of representation.

However, Rehfeld’s general theory of representation does not specify what representative do or should do in order to be recognized as a representative. And what exactly representatives do has been a hotly contested issue. In particular, a controversy has raged over whether representatives should act as delegates or trustees .

Historically, the theoretical literature on political representation has focused on whether representatives should act as delegates or as trustees . Representatives who are delegates simply follow the expressed preferences of their constituents. James Madison (1787–8) describes representative government as “the delegation of the government...to a small number of citizens elected by the rest.” Madison recognized that “Enlightened statesmen will not always be at the helm.” Consequently, Madison suggests having a diverse and large population as a way to decrease the problems with bad representation. In other words, the preferences of the represented can partially safeguard against the problems of faction.

In contrast, trustees are representatives who follow their own understanding of the best action to pursue. Edmund Burke (1790) is famous for arguing that

Parliament is not a congress of ambassadors from different and hostile interests, which interest each must maintain, as an agent and advocate, against other agents and advocates; but Parliament is a deliberative assembly of one nation, with one interest, that of the whole… You choose a member, indeed; but when you have chosen him he is not a member of Bristol, but he is a member of Parliament (115).

The delegate and the trustee conception of political representation place competing and contradictory demands on the behavior of representatives. [For a discussion of the similarities and differences between Madison’s and Burke’s conception of representation, see Pitkin 1967, 191–192.] Delegate conceptions of representation require representatives to follow their constituents’ preferences, while trustee conceptions require representatives to follow their own judgment about the proper course of action. Any adequate theory of representation must grapple with these contradictory demands.

Famously, Hanna Pitkin argues that theorists should not try to reconcile the paradoxical nature of the concept of representation. Rather, they should aim to preserve this paradox by recommending that citizens safeguard the autonomy of both the representative and of those being represented. The autonomy of the representative is preserved by allowing them to make decisions based on his or her understanding of the represented’s interests (the trustee conception of representation). The autonomy of those being represented is preserved by having the preferences of the represented influence evaluations of representatives (the delegate conception of representation). Representatives must act in ways that safeguard the capacity of the represented to authorize and to hold their representatives accountable and uphold the capacity of the representative to act independently of the wishes of the represented.

Objective interests are the key for determining whether the autonomy of representative and the autonomy of the represented have been breached. However, Pitkin never adequately specifies how we are to identify constituents’ objective interests. At points, she implies that constituents should have some say in what are their objective interests, but ultimately she merely shifts her focus away from this paradox to the recommendation that representatives should be evaluated on the basis of the reasons they give for disobeying the preferences of their constituents. For Pitkin, assessments about representatives will depend on the issue at hand and the political environment in which a representative acts. To understand the multiple and conflicting standards within the concept of representation is to reveal the futility of holding all representatives to some fixed set of guidelines. In this way, Pitkin concludes that standards for evaluating representatives defy generalizations. Moreover, individuals, especially democratic citizens, are likely to disagree deeply about what representatives should be doing.

Pitkin offers one of the most comprehensive discussions of the concept of political representation, attending to its contradictory character in her The Concept of Representation . This classic discussion of the concept of representation is one of the most influential and oft-cited works in the literature on political representation. (For a discussion of her influence, see Dovi 2016). Adopting a Wittgensteinian approach to language, Pitkin maintains that in order to understand the concept of political representation, one must consider the different ways in which the term is used. Each of these different uses of the term provides a different view of the concept. Pitkin compares the concept of representation to “ a rather complicated, convoluted, three–dimensional structure in the middle of a dark enclosure.” Political theorists provide “flash-bulb photographs of the structure taken from different angles” [1967, 10]. More specifically, political theorists have provided four main views of the concept of representation. Unfortunately, Pitkin never explains how these different views of political representation fit together. At times, she implies that the concept of representation is unified. At other times, she emphasizes the conflicts between these different views, e.g. how descriptive representation is opposed to accountability. Drawing on her flash-bulb metaphor, Pitkin argues that one must know the context in which the concept of representation is placed in order to determine its meaning. For Pitkin, the contemporary usage of the term “representation” can signficantly change its meaning.

For Pitkin, disagreements about representation can be partially reconciled by clarifying which view of representation is being invoked. Pitkin identifies at least four different views of representation: formalistic representation, descriptive representation, symbolic representation, and substantive representation. (For a brief description of each of these views, see chart below.) Each view provides a different approach for examining representation. The different views of representation can also provide different standards for assessing representatives. So disagreements about what representatives ought to be doing are aggravated by the fact that people adopt the wrong view of representation or misapply the standards of representation. Pitkin has in many ways set the terms of contemporary discussions about representation by providing this schematic overview of the concept of political representation.

1. Formalistic Representation : Brief Description . The institutional arrangements that precede and initiate representation. Formal representation has two dimensions: authorization and accountability. Main Research Question . What is the institutional position of a representative? Implicit Standards for Evaluating Representatives . None. ( Authorization ): Brief Description . The means by which a representative obtains his or her standing, status, position or office. Main Research Questions . What is the process by which a representative gains power (e.g., elections) and what are the ways in which a representative can enforce his or her decisions? Implicit Standards for Evaluating Representatives . No standards for assessing how well a representative behaves. One can merely assess whether a representative legitimately holds his or her position. pdf include--> ( Accountability ): Brief Description . The ability of constituents to punish their representative for failing to act in accordance with their wishes (e.g. voting an elected official out of office) or the responsiveness of the representative to the constituents. Main Research Question . What are the sanctioning mechanisms available to constituents? Is the representative responsive towards his or her constituents’ preferences? Implicit Standards for Evaluating Representatives . No standards for assessing how well a representative behaves. One can merely determine whether a representative can be sanctioned or has been responsive.

Brief Description . The ways that a representative “stands for” the represented — that is, the meaning that a representative has for those being represented.

Main Research Question . What kind of response is invoked by the representative in those being represented?

Implicit Standards for Evaluating Representatives . Representatives are assessed by the degree of acceptance that the representative has among the represented.

Brief Description . The extent to which a representative resembles those being represented.

Main Research Question . Does the representative look like, have common interests with, or share certain experiences with the represented?

Implicit Standards for Evaluating Representatives . Assess the representative by the accuracy of the resemblance between the representative and the represented.

Brief Description . The activity of representatives—that is, the actions taken on behalf of, in the interest of, as an agent of, and as a substitute for the represented.

Main Research Question . Does the representative advance the policy preferences that serve the interests of the represented?

Implicit Standards for Evaluating Representatives . Assess a representative by the extent to which policy outcomes advanced by a representative serve “the best interests” of their constituents.

One cannot overestimate the extent to which Pitkin has shaped contemporary understandings of political representation, especially among political scientists. For example, her claim that descriptive representation opposes accountability is often the starting point for contemporary discussions about whether marginalized groups need representatives from their groups.

Similarly, Pitkin’s conclusions about the paradoxical nature of political representation support the tendency among contemporary theorists and political scientists to focus on formal procedures of authorization and accountability (formalistic representation). In particular, there has been a lot of theoretical attention paid to the proper design of representative institutions (e.g. Amy 1996; Barber, 2001; Christiano 1996; Guinier 1994). This focus is certainly understandable, since one way to resolve the disputes about what representatives should be doing is to “let the people decide.” In other words, establishing fair procedures for reconciling conflicts provides democratic citizens one way to settle conflicts about the proper behavior of representatives. In this way, theoretical discussions of political representation tend to depict political representation as primarily a principal-agent relationship. The emphasis on elections also explains why discussions about the concept of political representation frequently collapse into discussions of democracy. Political representation is understood as a way of 1) establishing the legitimacy of democratic institutions and 2) creating institutional incentives for governments to be responsive to citizens.

David Plotke (1997) has noted that this emphasis on mechanisms of authorization and accountability was especially useful in the context of the Cold War. For this understanding of political representation (specifically, its demarcation from participatory democracy) was useful for distinguishing Western democracies from Communist countries. Those political systems that held competitive elections were considered to be democratic (Schumpeter 1976). Plotke questions whether such a distinction continues to be useful. Plotke recommends that we broaden the scope of our understanding of political representation to encompass interest representation and thereby return to debating what is the proper activity of representatives. Plotke’s insight into why traditional understandings of political representation resonated prior to the end of the Cold War suggests that modern understandings of political representation are to some extent contingent on political realities. For this reason, those who attempt to define political representation should recognize how changing political realities can affect contemporary understandings of political representation. Again, following Pitkin, ideas about political representation appear contingent on existing political practices of representation. Our understandings of representation are inextricably shaped by the manner in which people are currently being represented. For an informative discussion of the history of representation, see Monica Brito Vieira and David Runican’s Representation .

As mentioned earlier, theoretical discussions of political representation have focused mainly on the formal procedures of authorization and accountability within nation states, that is, on what Pitkin called formalistic representation. However, such a focus is no longer satisfactory due to international and domestic political transformations. [For an extensive discussion of international and domestic transformations, see Mark Warren and Dario Castioglione (2004).] Increasingly international, transnational and non-governmental actors play an important role in advancing public policies on behalf of democratic citizens—that is, acting as representatives for those citizens. Such actors “speak for,” “act for” and can even “stand for” individuals within a nation-state. It is no longer desirable to limit one’s understanding of political representation to elected officials within the nation-state. After all, increasingly state “contract out” important responsibilities to non-state actors, e.g. environmental regulation. As a result, elected officials do not necessarily possess “the capacity to act,” the capacity that Pitkin uses to identify who is a representative. So, as the powers of nation-state have been disseminated to international and transnational actors, elected representatives are not necessarily the agents who determine how policies are implemented. Given these changes, the traditional focus of political representation, that is, on elections within nation-states, is insufficient for understanding how public policies are being made and implemented. The complexity of modern representative processes and the multiple locations of political power suggest that contemporary notions of accountability are inadequate. Grant and Keohane (2005) have recently updated notions of accountability, suggesting that the scope of political representation needs to be expanded in order to reflect contemporary realities in the international arena. Michael Saward (2009) has proposed an innovative type of criteria that should be used for evaluating non-elective representative claims. John Dryzek and Simon Niemayer (2008) has proposed an alternative conception of representation, what he calls discursive representation, to reflect the fact that transnational actors represent discourses, not real people. By discourses, they mean “a set of categories and concepts embodying specific assumptions, judgments, contentions, dispositions, and capabilities.” The concept of discursive representation can potentially redeem the promise of deliberative democracy when the deliberative participation of all affected by a collective decision is infeasible.

Domestic transformations also reveal the need to update contemporary understandings of political representation. Associational life — social movements, interest groups, and civic associations—is increasingly recognized as important for the survival of representative democracies. The extent to which interest groups write public policies or play a central role in implementing and regulating policies is the extent to which the division between formal and informal representation has been blurred. The fluid relationship between the career paths of formal and informal representatives also suggests that contemporary realities do not justify focusing mainly on formal representatives. Mark Warren’s concept of citizen representatives (2008) opens up a theoretical framework for exploring how citizens represent themselves and serve in representative capacities.

Given these changes, it is necessary to revisit our conceptual understanding of political representation, specifically of democratic representation. For as Jane Mansbridge has recently noted, normative understandings of representation have not kept up with recent empirical research and contemporary democratic practices. In her important article “Rethinking Representation” Mansbridge identifies four forms of representation in modern democracies: promissory, anticipatory, gyroscopic and surrogacy. Promissory representation is a form of representation in which representatives are to be evaluated by the promises they make to constituents during campaigns. Promissory representation strongly resembles Pitkin’s discussion of formalistic representation. For both are primarily concerned with the ways that constituents give their consent to the authority of a representative. Drawing on recent empirical work, Mansbridge argues for the existence of three additional forms of representation. In anticipatory representation, representatives focus on what they think their constituents will reward in the next election and not on what they promised during the campaign of the previous election. Thus, anticipatory representation challenges those who understand accountability as primarily a retrospective activity. In gyroscopic representation, representatives “look within” to derive from their own experience conceptions of interest and principles to serve as a basis for their action. Finally, surrogate representation occurs when a legislator represents constituents outside of their districts. For Mansbridge, each of these different forms of representation generates a different normative criterion by which representatives should be assessed. All four forms of representation, then, are ways that democratic citizens can be legitimately represented within a democratic regime. Yet none of the latter three forms representation operates through the formal mechanisms of authorization and accountability. Recently, Mansbridge (2009) has gone further by suggesting that political science has focused too much on the sanctions model of accountability and that another model, what she calls the selection model, can be more effective at soliciting the desired behavior from representatives. According to Mansbridge, a sanction model of accountability presumes that the representative has different interests from the represented and that the represented should not only monitor but reward the good representative and punish the bad. In contrast, the selection model of accountability presumes that representatives have self-motivated and exogenous reasons for carrying out the represented’s wishes. In this way, Mansbridge broadens our understanding of accountability to allow for good representation to occur outside of formal sanctioning mechanisms.

Mansbridge’s rethinking of the meaning of representation holds an important insight for contemporary discussions of democratic representation. By specifying the different forms of representation within a democratic polity, Mansbridge teaches us that we should refer to the multiple forms of democratic representation. Democratic representation should not be conceived as a monolithic concept. Moreover, what is abundantly clear is that democratic representation should no longer be treated as consisting simply in a relationship between elected officials and constituents within her voting district. Political representation should no longer be understood as a simple principal-agent relationship. Andrew Rehfeld has gone farther, maintaining that political representation should no longer be territorially based. In other words, Rehfeld (2005) argues that constituencies, e.g. electoral districts, should not be constructed based on where citizens live.

Lisa Disch (2011) also complicates our understanding of democratic representation as a principal-agent relationship by uncovering a dilemma that arises between expectations of democratic responsiveness to constituents and recent empirical findings regarding the context dependency of individual constituents’ preferences. In response to this dilemma, Disch proposes a mobilization conception of political representation and develops a systemic understanding of reflexivity as the measure of its legitimacy.

By far, one of the most important shifts in the literature on representation has been the “constructivist turn.” Constructivist approaches to representation emphasize the representative’s role in creating and framing the identities and claims of the represented. Here Michael Saward’s The Representative Claim is exemplary. For Saward, representation entails a series of relationships: “A maker of representations (M) puts forward a subject (S) which stands for an object (O) which is related to a referent (R) and is offered to an audience (A)” (2006, 302). Instead of presuming a pre-existing set of interests of the represented that representatives “bring into” the political arena, Saward stresses how representative claim-making is a “deeply culturally inflected practice.” Saward explicitly denies that theorists can know what are the interests of the represented. For this reason, the represented should have the ultimate say in judging the claims of the representative. The task of the representative is to create claims that will resonate with appropriate audiences.

Saward therefore does not evaluate representatives by the extent to which they advance the preferences or interests of the represented. Instead he focuses on the institutional and collective conditions in which claim-making takes place. The constructivist turn examines the conditions for claim-making, not the activities of particular representatives.

Saward’s “constructivist turn” has generated a new research direction for both political theorists and empirical scientists. For example, Lisa Disch (2015) considers whether the constructivist turn is a “normative dead” end, that is, whether the epistemological commitments of constructivism that deny the ability to identify interests will undermine the normative commitments to democratic politics. Disch offers an alternative approach, what she calls “the citizen standpoint”. This standpoint does not mean taking at face value whomever or whatever citizens regard as representing them. Rather, it is “an epistemological and political achievement that does not exist spontaneously but develops out of the activism of political movements together with the critical theories and transformative empirical research to which they give rise” (2015, 493). (For other critical engagements with Saward’s work, see Schaap et al, 2012 and Nässtrom, 2011).

There have been a number of important advances in theorizing the concept of political representation. In particular, these advances call into question the traditional way of thinking of political representation as a principal-agent relationship. Most notably, Melissa Williams’ recent work has recommended reenvisioning the activity of representation in light of the experiences of historically disadvantaged groups. In particular, she recommends understanding representation as “mediation.” In particular, Williams (1998, 8) identifies three different dimensions of political life that representatives must “mediate:” the dynamics of legislative decision-making, the nature of legislator-constituent relations, and the basis for aggregating citizens into representable constituencies. She explains each aspect by using a corresponding theme (voice, trust, and memory) and by drawing on the experiences of marginalized groups in the United States. For example, drawing on the experiences of American women trying to gain equal citizenship, Williams argues that historically disadvantaged groups need a “voice” in legislative decision-making. The “heavily deliberative” quality of legislative institutions requires the presence of individuals who have direct access to historically excluded perspectives.

In addition, Williams explains how representatives need to mediate the representative-constituent relationship in order to build “trust.” For Williams, trust is the cornerstone for democratic accountability. Relying on the experiences of African-Americans, Williams shows the consistent patterns of betrayal of African-Americans by privileged white citizens that give them good reason for distrusting white representatives and the institutions themselves. For Williams, relationships of distrust can be “at least partially mended if the disadvantaged group is represented by its own members”(1998, 14). Finally, representation involves mediating how groups are defined. The boundaries of groups according to Williams are partially established by past experiences — what Williams calls “memory.” Having certain shared patterns of marginalization justifies certain institutional mechanisms to guarantee presence.

Williams offers her understanding of representation as mediation as a supplement to what she regards as the traditional conception of liberal representation. Williams identifies two strands in liberal representation. The first strand she describes as the “ideal of fair representation as an outcome of free and open elections in which every citizen has an equally weighted vote” (1998, 57). The second strand is interest-group pluralism, which Williams describes as the “theory of the organization of shared social interests with the purpose of securing the equitable representation … of those groups in public policies” ( ibid .). Together, the two strands provide a coherent approach for achieving fair representation, but the traditional conception of liberal representation as made up of simply these two strands is inadequate. In particular, Williams criticizes the traditional conception of liberal representation for failing to take into account the injustices experienced by marginalized groups in the United States. Thus, Williams expands accounts of political representation beyond the question of institutional design and thus, in effect, challenges those who understand representation as simply a matter of formal procedures of authorization and accountability.

Another way of reenvisioning representation was offered by Nadia Urbinati (2000, 2002). Urbinati argues for understanding representation as advocacy. For Urbinati, the point of representation should not be the aggregation of interests, but the preservation of disagreements necessary for preserving liberty. Urbinati identifies two main features of advocacy: 1) the representative’s passionate link to the electors’ cause and 2) the representative’s relative autonomy of judgment. Urbinati emphasizes the importance of the former for motivating representatives to deliberate with each other and their constituents. For Urbinati the benefit of conceptualizing representation as advocacy is that it improves our understanding of deliberative democracy. In particular, it avoids a common mistake made by many contemporary deliberative democrats: focusing on the formal procedures of deliberation at the expense of examining the sources of inequality within civil society, e.g. the family. One benefit of Urbinati’s understanding of representation is its emphasis on the importance of opinion and consent formation. In particular, her agonistic conception of representation highlights the importance of disagreements and rhetoric to the procedures, practices, and ethos of democracy. Her account expands the scope of theoretical discussions of representation away from formal procedures of authorization to the deliberative and expressive dimensions of representative institutions. In this way, her agonistic understanding of representation provides a theoretical tool to those who wish to explain how non-state actors “represent.”

Other conceptual advancements have helped clarify the meaning of particular aspects of representation. For instance, Andrew Rehfeld (2009) has argued that we need to disaggregate the delegate/trustee distinction. Rehfeld highlights how representatives can be delegates and trustees in at least three different ways. For this reason, we should replace the traditional delegate/trustee distinction with three distinctions (aims, source of judgment, and responsiveness). By collapsing these three different ways of being delegates and trustees, political theorists and political scientists overlook the ways in which representatives are often partial delegates and partial trustees.

Other political theorists have asked us to rethink central aspects of our understanding of democratic representation. In Inclusion and Democracy Iris Marion Young asks us to rethink the importance of descriptive representation. Young stresses that attempts to include more voices in the political arena can suppress other voices. She illustrates this point using the example of a Latino representative who might inadvertently represent straight Latinos at the expense of gay and lesbian Latinos (1986, 350). For Young, the suppression of differences is a problem for all representation (1986, 351). Representatives of large districts or of small communities must negotiate the difficulty of one person representing many. Because such a difficulty is constitutive of representation, it is unreasonable to assume that representation should be characterized by a “relationship of identity.” The legitimacy of a representative is not primarily a function of his or her similarities to the represented. For Young, the representative should not be treated as a substitute for the represented. Consequently, Young recommends reconceptualizing representation as a differentiated relationship (2000, 125–127; 1986, 357). There are two main benefits of Young’s understanding of representation. First, her understanding of representation encourages us to recognize the diversity of those being represented. Second, her analysis of representation emphasizes the importance of recognizing how representative institutions include as well as they exclude. Democratic citizens need to remain vigilant about the ways in which providing representation for some groups comes at the expense of excluding others. Building on Young’s insight, Suzanne Dovi (2009) has argued that we should not conceptualize representation simply in terms of how we bring marginalized groups into democratic politics; rather, democratic representation can require limiting the influence of overrepresented privileged groups.

Moreover, based on this way of understanding political representation, Young provides an alterative account of democratic representation. Specifically, she envisions democratic representation as a dynamic process, one that moves between moments of authorization and moments of accountability (2000, 129). It is the movement between these moments that makes the process “democratic.” This fluidity allows citizens to authorize their representatives and for traces of that authorization to be evident in what the representatives do and how representatives are held accountable. The appropriateness of any given representative is therefore partially dependent on future behavior as well as on his or her past relationships. For this reason, Young maintains that evaluation of this process must be continuously “deferred.” We must assess representation dynamically, that is, assess the whole ongoing processes of authorization and accountability of representatives. Young’s discussion of the dynamic of representation emphasizes the ways in which evaluations of representatives are incomplete, needing to incorporate the extent to which democratic citizens need to suspend their evaluations of representatives and the extent to which representatives can face unanticipated issues.

Another insight about democratic representation that comes from the literature on descriptive representation is the importance of contingencies. Here the work of Jane Mansbridge on descriptive representation has been particularly influential. Mansbridge recommends that we evaluate descriptive representatives by contexts and certain functions. More specifically, Mansbridge (1999, 628) focuses on four functions and their related contexts in which disadvantaged groups would want to be represented by someone who belongs to their group. Those four functions are “(1) adequate communication in contexts of mistrust, (2) innovative thinking in contexts of uncrystallized, not fully articulated, interests, … (3) creating a social meaning of ‘ability to rule’ for members of a group in historical contexts where the ability has been seriously questioned and (4) increasing the polity’s de facto legitimacy in contexts of past discrimination.” For Mansbridge, descriptive representatives are needed when marginalized groups distrust members of relatively more privileged groups and when marginalized groups possess political preferences that have not been fully formed. The need for descriptive representation is contingent on certain functions.

Mansbridge’s insight about the contingency of descriptive representation suggests that at some point descriptive representatives might not be necessary. However, she doesn’t specify how we are to know if interests have become crystallized or trust has formed to the point that the need for descriptive representation would be obsolete. Thus, Mansbridge’s discussion of descriptive representation suggests that standards for evaluating representatives are fluid and flexible. For an interesting discussion of the problems with unified or fixed standards for evaluating Latino representatives, see Christina Beltran’s The Trouble with Unity .

Mansbridge’s discussion of descriptive representation points to another trend within the literature on political representation — namely, the trend to derive normative accounts of representation from the representative’s function. Russell Hardin (2004) captured this trend most clearly in his position that “if we wish to assess the morality of elected officials, we must understand their function as our representatives and then infer how they can fulfill this function.” For Hardin, only an empirical explanation of the role of a representative is necessary for determining what a representative should be doing. Following Hardin, Suzanne Dovi (2007) identifies three democratic standards for evaluating the performance of representatives: those of fair-mindedness, critical trust building, and good gate-keeping. In Ruling Passions , Andrew Sabl (2002) links the proper behavior of representatives to their particular office. In particular, Sabl focuses on three offices: senator, organizer and activist. He argues that the same standards should not be used to evaluate these different offices. Rather, each office is responsible for promoting democratic constancy, what Sabl understands as “the effective pursuit of interest.” Sabl (2002) and Hardin (2004) exemplify the trend to tie the standards for evaluating political representatives to the activity and office of those representatives.

There are three persistent problems associated with political representation. Each of these problems identifies a future area of investigation. The first problem is the proper institutional design for representative institutions within democratic polities. The theoretical literature on political representation has paid a lot of attention to the institutional design of democracies. More specifically, political theorists have recommended everything from proportional representation (e.g. Guinier, 1994 and Christiano, 1996) to citizen juries (Fishkin, 1995). However, with the growing number of democratic states, we are likely to witness more variation among the different forms of political representation. In particular, it is important to be aware of how non-democratic and hybrid regimes can adopt representative institutions to consolidate their power over their citizens. There is likely to be much debate about the advantages and disadvantages of adopting representative institutions.

This leads to a second future line of inquiry — ways in which democratic citizens can be marginalized by representative institutions. This problem is articulated most clearly by Young’s discussion of the difficulties arising from one person representing many. Young suggests that representative institutions can include the opinions, perspectives and interests of some citizens at the expense of marginalizing the opinions, perspectives and interests of others. Hence, a problem with institutional reforms aimed at increasing the representation of historically disadvantaged groups is that such reforms can and often do decrease the responsiveness of representatives. For instance, the creation of black districts has created safe zones for black elected officials so that they are less accountable to their constituents. Any decrease in accountability is especially worrisome given the ways citizens are vulnerable to their representatives. Thus, one future line of research is examining the ways that representative institutions marginalize the interests, opinions and perspectives of democratic citizens.

In particular, it is necessary for to acknowledge the biases of representative institutions. While E. E. Schattschneider (1960) has long noted the class bias of representative institutions, there is little discussion of how to improve the political representation of the disaffected — that is, the political representation of those citizens who do not have the will, the time, or political resources to participate in politics. The absence of such a discussion is particularly apparent in the literature on descriptive representation, the area that is most concerned with disadvantaged citizens. Anne Phillips (1995) raises the problems with the representation of the poor, e.g. the inability to define class, however, she argues for issues of class to be integrated into a politics of presence. Few theorists have taken up Phillip’s gauntlet and articulated how this integration of class and a politics of presence is to be done. Of course, some have recognized the ways in which interest groups, associations, and individual representatives can betray the least well off (e.g. Strolovitch, 2004). And some (Dovi, 2003) have argued that descriptive representatives need to be selected based on their relationship to citizens who have been unjustly excluded and marginalized by democratic politics. However, it is unclear how to counteract the class bias that pervades domestic and international representative institutions. It is necessary to specify the conditions under which certain groups within a democratic polity require enhanced representation. Recent empirical literature has suggested that the benefits of having descriptive representatives is by no means straightforward (Gay, 2002).

A third and final area of research involves the relationship between representation and democracy. Historically, representation was considered to be in opposition with democracy [See Dahl (1989) for a historical overview of the concept of representation]. When compared to the direct forms of democracy found in the ancient city-states, notably Athens, representative institutions appear to be poor substitutes for the ways that citizens actively ruled themselves. Barber (1984) has famously argued that representative institutions were opposed to strong democracy. In contrast, almost everyone now agrees that democratic political institutions are representative ones.

Bernard Manin (1997)reminds us that the Athenian Assembly, which often exemplifies direct forms of democracy, had only limited powers. According to Manin, the practice of selecting magistrates by lottery is what separates representative democracies from so-called direct democracies. Consequently, Manin argues that the methods of selecting public officials are crucial to understanding what makes representative governments democratic. He identifies four principles distinctive of representative government: 1) Those who govern are appointed by election at regular intervals; 2) The decision-making of those who govern retains a degree of independence from the wishes of the electorate; 3) Those who are governed may give expression to their opinions and political wishes without these being subject to the control of those who govern; and 4) Public decisions undergo the trial of debate (6). For Manin, historical democratic practices hold important lessons for determining whether representative institutions are democratic.

While it is clear that representative institutions are vital institutional components of democratic institutions, much more needs to be said about the meaning of democratic representation. In particular, it is important not to presume that all acts of representation are equally democratic. After all, not all acts of representation within a representative democracy are necessarily instances of democratic representation. Henry Richardson (2002) has explored the undemocratic ways that members of the bureaucracy can represent citizens. [For a more detailed discussion of non-democratic forms of representation, see Apter (1968). Michael Saward (2008) also discusses how existing systems of political representation do not necessarily serve democracy.] Similarly, it is unclear whether a representative who actively seeks to dismantle democratic institutions is representing democratically. Does democratic representation require representatives to advance the preferences of democratic citizens or does it require a commitment to democratic institutions? At this point, answers to such questions are unclear. What is certain is that democratic citizens are likely to disagree about what constitutes democratic representation.

One popular approach to addressing the different and conflicting standards used to evaluate representatives within democratic polities, is to simply equate multiple standards with democratic ones. More specifically, it is argued that democratic standards are pluralistic, accommodating the different standards possessed and used by democratic citizens. Theorists who adopt this approach fail to specify the proper relationship among these standards. For instance, it is unclear how the standards that Mansbridge identifies in the four different forms of representation should relate to each other. Does it matter if promissory forms of representation are replaced by surrogate forms of representation? A similar omission can be found in Pitkin: although Pitkin specifies there is a unified relationship among the different views of representation, she never describes how the different views interact. This omission reflects the lacunae in the literature about how formalistic representation relates to descriptive and substantive representation. Without such a specification, it is not apparent how citizens can determine if they have adequate powers of authorization and accountability.

Currently, it is not clear exactly what makes any given form of representation consistent, let alone consonant, with democratic representation. Is it the synergy among different forms or should we examine descriptive representation in isolation to determine the ways that it can undermine or enhance democratic representation? One tendency is to equate democratic representation simply with the existence of fluid and multiple standards. While it is true that the fact of pluralism provides justification for democratic institutions as Christiano (1996) has argued, it should no longer presumed that all forms of representation are democratic since the actions of representatives can be used to dissolve or weaken democratic institutions. The final research area is to articulate the relationship between different forms of representation and ways that these forms can undermine democratic representation.

• Andeweg, Rudy B., and Jacques J.A. Thomassen, 2005. “Modes of Political Representation: Toward a new typology,” Legislative Studies Quarterly , 30(4): 507–528.
• Ankersmit, Franklin Rudolph, 2002. Political Representation , Stanford: Stanford University Press.
• Alcoff, Linda, 1991. “The Problem of Speaking for Others,” Cultural Critique , Winter: 5–32.
• Alonso, Sonia, John Keane, and Wolfgang Merkel (eds.), 2011. The Future of Representative Democracy , Cambridge: Cambridge University Press.
• Beitz, Charles, 1989. Political Equality , Princeton, NJ: Princeton University Press. [Chapter 6 is on ‘Representation’]
• Burke, Edmund, 1790 [1968]. Reflections on the Revolution in France , London: Penguin Books.
• Dahl, Robert A., 1989. Democracy and Its Critics , New Haven: Yale University.
• Disch, Lisa, 2015. “The Constructivist Turn in Democratic Representation: A Normative Dead-End?,” Constellations , 22(4): 487–499.
• Dovi, Suzanne, 2007. The Good Representative , New York: Wiley-Blackwell Publishing.
• Downs, Anthony, 1957. An Economic Theory of Democracy , New York: Harper.
• Dryzek, John and Simon Niemeyer, 2008. “Discursive Representation,” American Political Science Review , 102(4): 481–493.
• Hardin, Russell, 2004. “Representing Ignorance,” Social Philosophy and Policy , 21: 76–99.
• Lublin, David, 1999. The Paradox of Representation: Racial Gerrymandering and Minority Interests in Congress , Princeton: Princeton University Press.
• Madison, James, Alexander Hamilton and John Jay, 1787–8 [1987]. The Federalist Papers , Isaac Kramnick (ed.), Harmondsworth: Penguin.
• Mansbridge, Jane, 2003. “Rethinking Representation,” American Political Science Review , 97(4): 515–28.
• Manin, Bernard, 1997. The Principles of Representative Government , Cambridge: Cambridge University Press.
• Nässtrom, Sofia, 2011. “Where is the representative turn going?” European journal of political theory, , 10(4): 501–510.
• Pennock, J. Roland and John Chapman (eds.), 1968. Representation , New York: Atherton Press.
• Pitkin, Hanna Fenichel, 1967. The Concept of Representation , Berkeley: University of California.
• Plotke, David, 1997. “Representation is Democracy,” Constellations , 4: 19–34.
• Rehfeld, Andrew, 2005. The Concept of Constituency: Political Representation, Democratic Legitimacy and Institutional Design , Cambridge: Cambridge University Press.
• –––, 2006. “Towards a General Theory of Political Representation,” The Journal of Politics , 68: 1–21.
• Rosenstone, Steven and John Hansen, 1993. Mobilization, Participation, and Democracy in America , New York: MacMillian Publishing Company.
• Runciman, David, 2007. “The Paradox of Political Representation,” Journal of Political Philosophy , 15: 93–114.
• Saward, Michael, 2014. “Shape-shifting representation”. American Political Science Review , 108(4): 723–736.
• –––, 2010. The Representative Claim , Oxford: Oxford University Press.
• –––, 2008. “Representation and democracy: revisions and possibilities,” Sociology compass , 2(3): 1000–1013.
• –––, 2006. “The representative claim”. Contemporary political theory , 5(3): 297–318.
• Sabl, Andrew, 2002. Ruling Passions: Political Offices and Democratic Ethics , Princeton: Princeton University Press.
• Schaap, Andrew, Thompson, Simon, Disch, Lisa, Castiglione, Dario and Saward, Michael, 2012. “Critical exchange on Michael Saward’s The Representative Claim,” Contemporary Political Theory , 11(1): 109–127.
• Schattschneider, E. E., 1960. The Semisovereign People , New York: Holt, Rinehart, and Winston.
• Schumpeter, Joseph, 1976. Capitalism, Socialism, and Democracy , London: Allen and Unwin.
• Schwartz, Nancy, 1988. The Blue Guitar: Political Representation and Community , Chicago: University of Chicago Press.
• Shapiro, Ian, Susan C. Stokes, Elisabeth Jean Wood and Alexander S. Kirshner (eds.), 2009. Political Representation , Cambridge: Cambridge University Press.
• Urbinati, Nadia, 2000. “Representation as Advocacy: A Study of Democratic Deliberation,” Political Theory , 28: 258–786.
• Urbinati, Nadia and Mark Warren, 2008. “The Concept of Representation in Contemporary Democratic Theory,” Annual Review of Political Science , 11: 387–412
• Vieira, Monica and David Runciman, 2008. Representation , Cambridge: Polity Press.
• Vieira, Monica (ed.), 2017. Reclaiming Representation: Contemporary Advances in the Theory of Political Representation , New York: Routledge Press.
• Warren, Mark and Dario Castiglione, 2004. “The Transformation of Democratic Representation,” Democracy and Society , 2(1): 5–22.
• Barber, Benjamin, 1984. Strong Democracy , Los Angeles, CA: University of California Press.
• Dryzek, John, 1996. “Political Inclusion and the Dynamics of Democratization,” American Political Science Review , 90 (September): 475–487.
• Pateman, Carole, 1970. Participation and Democratic Theory , Cambridge: Cambridge University Press.
• Rousseau, Jean Jacques, 1762, The Social Contract , Judith Masters and Roger Masters (trans.), New York: St. Martins Press, 1978.
• Saward, Michael, 2008. “Representation and Democracy: Revisions and Possibilities,” Sociology Compass , 2: 1000–1013.
• Apter, David, 1968. “Notes for a Theory of Nondemocratic Representation,” in Nomos X , Chapter 19, pp. 278–317.
• Brown, Mark, 2006. “Survey Article: Citizen Panels and the Concept of Representation,” Journal of Political Philosophy , 14: 203–225.
• Cohen, Joshua and Joel Rogers, 1995. Associations and Democracy (The Real Utopias Project: Volume 1), Erik Olin Wright (ed.), London: Verso.
• Dalton, Russell J., and Martin P. Wattenberg (eds.), 2002. Parties without partisans: Political change in advanced industrial democracies , Oxford: Oxford University Press.
• Montanaro, L., 2012. “The Democratic Legitimacy of Self-appointed Representatives,” The Journal of Politics , 74(4): 1094–1107.
• Ryden, David K., 1996. Representation in Crisis: The Constitution, Interest Groups, and Political Parties , Albany: State University of New York Press.
• Truman, David, 1951. The Governmental Process , New York: Knopf.
• Saward, Michael, 2009. “ Authorisation and Authenticity: Representation and the Unelected,” Journal of Political Philosophy , 17: 1–22.
• Steunenberg, Bernard and J. J. A.Thomassen, 2002. The European Parliament : Moving Toward Democracy in the EU , Oxford: Rowman & Littlefield.
• Schmitter, Philippe, 2000. “Representation,” in How to democratize the European Union and Why Bother? , Lanham, MD: Rowman and Littlefield, Ch. 3. pp. 53–74.
• Street, John, 2004. “Celebrity politicians: popular culture and political representation,” The British Journal of Politics and International Relations , 6(4): 435–452.
• Strolovitch, Dara Z., 2007. Affirmative Advocacy: Race, Class, and Gender in Interest Group Politics , Chicago: Chicago University Press.
• Tormey, S., 2012. “Occupy Wall Street: From representation to post-representation,” Journal of Critical Globalisation Studies , 5: 132–137.
• Richardson, Henry, 2002. “Representative government,” in Democratic Autonomy , Oxford: Oxford University Press, Ch. 14, pp. 193–202
• Runciman, David, 2010. “Hobbes’s Theory of Representation: anti-democratic or protodemoratic,” in Political Representation , Ian Shapiro, Susan C. Stokes, Elisabeth Jean Wood, and Alexander Kirshner (eds.), Cambridge: Cambridge University Press.
• Warren, Mark, 2001. Democracy and Association , Princeton, NJ: Princeton University Press.
• –––, 2008. “Citizen Representatives,” in Designing Deliberative Democracy: The British ColumbiaCitizens’ Assembly , Mark Warren and Hilary Pearse (eds.), Cambridge: Cambridge University Press, 50–69.
• Warren, Mark and Dario Castiglione, 2004. “The Transformation of Democratic Representation,” Democracy and Society , 2(I): 5, 20–22.
• Amy, Douglas, 1996. Real Choices/New Voices: The Case for Proportional Elections in the United States , New York: Columbia University Press.
• Barber, Kathleen, 2001. A Right to Representation: Proportional Election Systems for the 21 st Century , Columbia: Ohio University Press.
• Canon, David, 1999. Race, Redistricting, and Representation: The Unintended Consequences of Black Majority Districts , Chicago: University of Chicago Press.
• Christiano, Thomas, 1996. The Rule of the Many , Boulder: Westview Press.
• Cotta, Maurizio and Heinrich Best (eds.), 2007. Democratic Representation in Europe Diversity, Change, and Convergence , Oxford: Oxford University Press.
• Guinier, Lani, 1994. The Tyranny of the Majority: Fundamental Fairness in Representative Democracy , New York: Free Press.
• Przworksi, Adam, Susan C. Stokes, and Bernard Manin (eds.), 1999. Democracy, Accountability, and Representation , Cambridge: Cambridge University Press.
• Thompson, Dennis, 2002. Just Elections , Chicago: University of Chicago Press.
• Jacobs, Lawrence R. and Robert Y. Shapiro, 2000. Politicians Don’t Pander: Political Manipulation and the Loss of Democratic Responsiveness , Chicago: University of Chicago Press.
• Grant, Ruth and Robert O. Keohane, 2005. “Accountability and Abuses of Power in World Politics,” American Political Science Review , 99 (February): 29–44.
• Mansbridge, Jane, 2004. “Representation Revisited: Introduction to the Case Against Electoral Accountability,” Democracy and Society , 2(I): 12–13.
• –––, 2009. “A Selection Model of Representation,” Journal of Political Philosophy , 17(4): 369–398.
• Pettit, Philip, 2010. “Representation, Responsive and Indicative,” Constellations , 17(3): 426–434.
• Fishkin, John, 1995. The Voice of the People: Public Opinion and Democracy , New Haven, CT: Yale University Press.
• Gutmann, Amy and Dennis Thompson, 2004. Why Deliberative Democracy? , Princeton: Princeton University Press.
• Hibbing, John and Elizabeth Theiss-Morse, 2002. Stealth Democracy , Cambridge: Cambridge University Press.
• Saward, Michael (ed.), 2000. Democratic Innovation: Deliberation, Representation and Association , London: Routledge.
• Severs, E., 2010. “Representation As Claims-Making. Quid Responsiveness?” Representation , 46(4): 411–423.
• Williams, Melissa, 2000. “The Uneasy Alliance of Group Representation and Deliberative Democracy,” in Citizenship in Diverse Societies , W. Kymlicka and Wayne Norman (eds.), Oxford: Oxford University Press, Ch 5. pp. 124–153.
• Young, Iris Marion, 1999. “Justice, Inclusion, and Deliberative Democracy” in Deliberative Politics , Stephen Macedo (ed.), Oxford: Oxford University.
• Bentran, Cristina, 2010. The Trouble with Unity: Latino Politics and the Creation of Identity , Oxford: Oxford University Press.
• Celis, Karen, Sarah Childs, Johanna Kantola and Mona Lena Krook, 2008, “Rethinking Women’s Substantive Representation,” Representation , 44(2): 99–110.
• Childs Sarah, 2008. Women and British Party Politics: Descriptive, Substantive and Symbolic Representation , London: Routledge.
• Dovi, Suzanne, 2002. “Preferable Descriptive Representatives: Or Will Just Any Woman, Black, or Latino Do?,” American Political Science Review , 96: 745–754.
• –––, 2007. “Theorizing Women’s Representation in the United States?,” Politics and Gender , 3(3): 297–319. doi: 10.1017/S1743923X07000281
• –––, 2009. “In Praise of Exclusion,” Journal of Politics , 71 (3): 1172–1186.
• –––, 2016. “Measuring Representation: Rethinking the Role of Exclusion” Political Representation , Marc Bühlmann and Jan Fivaz (eds.), London: Routledge.
• Fenno, Richard F., 2003. Going Home: Black Representatives and Their Constituents , Chicago, IL: University of Chicago Press.
• Gay, Claudine, 2002. “Spirals of Trust?,” American Journal of Political Science , 4: 717–32.
• Gould, Carol, 1996. “Diversity and Democracy: Representing Differences,” in Democracy and Difference: Contesting the Boundaries of the Political , Seyla Benhabib (ed.), Princeton: Princeton University, pp. 171–186.
• Htun, Mala, 2004. “Is Gender like Ethnicity? The Political Representation of Identity Groups,” Perspectives on Politics , 2: 439–458.
• Mansbridge, Jane, 1999. “Should Blacks Represent Blacks and Women Represent Women? A Contingent ‘Yes’,” The Journal of Politics , 61: 628–57.
• –––, 2003. “Rethinking Representation,” American Political Science Review , 97: 515–528.
• Phillips, Anne, 1995. Politics of Presence , New York: Clarendon.
• –––, 1998. “Democracy and Representation: Or, Why Should It Matter Who Our Representatives Are?,” in Feminism and Politics , Oxford: Oxford University. pp. 224–240.
• Pitkin, Hanna, 1967. The Concept of Representation , Los Angeles: University of Press.
• Sapiro, Virginia, 1981. “When are Interests Interesting?,” American Political Science Review , 75 (September): 701–721.
• Strolovitch, Dara Z., 2004. “Affirmative Representation,” Democracy and Society , 2: 3–5.
• Swain, Carol M., 1993. Black Faces, Black Interests: The Representation of African Americans in Congress , Cambridge, MA: Harvard University.
• Thomas, Sue, 1991. “The Impact of Women on State Legislative Policies,” Journal of Politics , 53 (November): 958–976.
• –––, 1994. How Women Legislate , New York: Oxford University Press.
• Weldon, S. Laurel, 2002. “Beyond Bodies: Institutional Sources of Representation for Women in Democratic Policymaking,” Journal of Politics , 64(4): 1153–1174.
• Williams, Melissa, 1998. Voice, Trust, and Memory: Marginalized Groups and the Failings of Liberal Representation , Princeton, NJ: Princeton University.
• Young, Iris Marion, 1986. “Deferring Group Representation,” Nomos: Group Rights , Will Kymlicka and Ian Shapiro (eds.), New York: New York University Press, pp. 349–376.
• –––, 1990. Justice and the Politics of Difference , Princeton, NJ: Princeton University
• –––, 2000. Inclusion and Democracy , Oxford: Oxford University Press.

G. Democratic Representation

• Castiglione, D., 2015. “Trajectories and Transformations of the Democratic Representative System”. Global Policy , 6(S1): 8–16.
• Disch, Lisa, 2011. “Toward a Mobilization Conception of Democratic Representation,” American Political Science Review , 105(1): 100–114.
• –––, 2012. “Democratic representation and the constituency paradox,” Perspectives on Politics , 10(3): 599–616.
• –––, 2016. “Hanna Pitkin, The Concept of Representation,” The Oxford Handbook of Classics in Contemporary Political Theory , Jacob Levy (ed.), Oxford: Oxford University Press. doi: 10.1093/oxfordhb/9780198717133.013.24
• Mansbridge, Jane, 2003. “Rethinking Representation,” American Political Science Review , 97: 515–528.
• Näsström, Sofia, 2006. “Representative democracy as tautology: Ankersmit and Lefort on representation,” European Journal of Political Theory , 5(3): 321–342.
• Urbinati, Nadia, 2011. “Political Representation as Democratic Process,” Redescriptions (Yearbook of Political Thought and Conceptual History: Volume 10), Kari Palonen (ed.), Helsinki: Transaction Publishers.

How to cite this entry . Preview the PDF version of this entry at the Friends of the SEP Society . Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers , with links to its database.

• FairVote Program for Representative Government
• Proportional Representation Library , provides readings proportional representation elections created by Prof. Douglas J. Amy, Dept. of Politics, Mount Holyoke College
• Representation , an essay by Ann Marie Baldonado on the Postcolonial Studies website at Emory University.
• Representation: John Locke, Second Treatise, §§ 157–58 , in The Founders’ Constitution at the University of Chicago Press
• Popular Basis of Political Authority: David Hume, Of the Original Contract , in The Founders’ Constitution at the University of Chicago Press

Burke, Edmund | democracy

Copyright © 2018 by Suzanne Dovi < sdovi @ email . arizona . edu >

• Accessibility

Support SEP

Mirror sites.

View this site from another server:

• Info about mirror sites

The Stanford Encyclopedia of Philosophy is copyright © 2023 by The Metaphysics Research Lab , Department of Philosophy, Stanford University

Library of Congress Catalog Data: ISSN 1095-5054

Browse Course Material

Course info.

• Prof. Pavel Etingof

Departments

• Mathematics

As Taught In

• Algebra and Number Theory
• Linear Algebra

Learning Resource Types

Introduction to representation theory, lecture notes.

Students are assigned readings in these lecture notes each week. The present lecture notes arose from a representation theory course given by Prof. Etingof in March 2004 within the framework of the Clay Mathematics Institute Research Academy for high school students. The students in that course — Oleg Golberg, Sebastian Hensel, Tiankai Liu, Alex Schwendner, Elena Yudovina, and Dmitry Vaintrob — co-authored the lecture notes which are published here with their permission.

The book Introduction to Representation Theory based on these notes was published by the American Mathematical Society in 2016. A complete file of the book (PDF - 1.1MB) is on Prof. Etingof’s webpage. [Please note: This file cannot be posted on any website not belonging to the authors.]

Complete Lecture Notes ( PDF - 1.3MB )

Introduction ( PDF )

Chapter 1: basic notions of representation theory ( pdf ).

1.1 What is representation theory? 1.2 Algebras 1.3 Representations 1.4 Ideals 1.5 Quotients 1.6 Algebras defined by generators and relations 1.7 Examples of algebras 1.8 Quivers 1.9 Lie algebras 1.10 Tensor products 1.11 The tensor algebra 1.12 Hilbert’s third problem 1.13 Tensor products and duals of representations of Lie algebras 1.14 Representations of sl(2) 1.15 Problems on Lie algebras

Chapter 2: General Results of Representation Theory ( PDF )

2.1 Subrepresentations in semisimple representations 2.2 The density theorem 2.3 Representations of direct sums of matrix algebras 2.4 Filtrations 2.5 Finite dimensional algebras 2.6 Characters of representations 2.7 The Jordan-Hölder theorem 2.8 The Krull-Schmidt theorem 2.9 Problems 2.10 Representations of tensor products

Chapter 3: Representations of Finite Groups: Basic Results ( PDF )

3.1 Maschke’s Theorem 3.2 Characters 3.3 Examples 3.4 Duals and tensor products of representations 3.5 Orthogonality of characters 3.6 Unitary representations. Another proof of Maschke’s theorem for complex representations 3.7 Orthogonality of matrix elements 3.8 Character tables, examples 3.9 Computing tensor product multiplicities using character tables 3.10 Problems

Chapter 4: Representations of Finite Groups: Further Results ( PDF )

4.1 Frobenius-Schur indicator 4.2 Frobenius determinant 4.3 Algebraic numbers and algebraic integers 4.4 Frobenius divisibility 4.5 Burnside’s theorem 4.6 Representations of products 4.7 Virtual representations 4.8 Induced representations 4.9 The Mackey formula 4.10 Frobenius reciprocity 4.11 Examples 4.12 Representations of _S_ n 4.13 Proof of theorem 4.36 4.14 Induced representations for _S_ n 4.15 The Frobenius character formula 4.16 Problems 4.17 The hook length formula 4.18 Schur-Weyl duality 4.19 Schur-Weyl duality for GL (V) 4.20 Schur polynomials 4.21 The characters of L λ 4.22 Polynomial representations of GL (V) 4.23 Problems 4.24 Representations of _GL_ 2 (F q )

4.24.1 Conjugacy classes in _GL_ 2 (F q ) 4.24.2 1-dimensional representations 4.24.3 Principal series representations 4.24.4 Complementary series representations

4.25 Artin’s theorem 4.26 Representations of semidirect products

Chapter 5: Quiver Representations ( PDF )

5.1 Problems 5.2 Indecomposable representations of the quivers A1,A2,A3 5.3 Indecomposable representations of the quiver D 4 5.4 Roots 5.5 Gabriel’s theorem 5.6 Reflection functors 5.7 Coxeter elements 5.8 Proof of Gabriel’s theorem 5.9 Problems

Chapter 6: Introduction to Categories ( PDF )

6.1 The definition of a category 6.2 Functors 6.3 Morphisms of functors 6.4 Equivalence of categories 6.5 Representable functors 6.6 Adjoint functors 6.7 Abelian categories 6.8 Exact functors

Chapter 7: Structure of Finite Dimensional Algebras ( PDF )

7.1 Projective modules 7.2 Lifting of idempotents 7.3 Projective covers

You are leaving MIT OpenCourseWare

Jerome Bruner’s Theory Of Learning And Cognitive Development

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

Jerome Bruner believed that children construct knowledge and meaning through active experience with the world around them. He emphasized the role of culture and language in cognitive development, which occurs in a spiral fashion with children revisiting basic concepts at increasing levels of complexity and abstraction.

Bruner’s Ideas

• Like  Ausubel (and other cognitive psychologists), Bruner sees the learner as an active agent; emphasizing the importance of existing schemata in guiding learning.
• Bruner argues that students should discern for themselves the structure of subject content – discovering the links and relationships between different facts, concepts and theories (rather than the teacher simply telling them).
• Bruner (1966) hypothesized that the usual course of intellectual development moves through three stages: enactive, iconic, and symbolic, in that order. However, unlike Piaget’s stages, Bruner did not contend that these stages were necessarily age-dependent, or invariant.
• Piaget and, to an extent, Ausubel, contended that the child must be ready, or made ready, for the subject matter. But Bruner contends just the opposite. According to his theory, the fundamental principles of any subject can be taught at any age, provided the material is converted to a form (and stage) appropriate to the child.
• The notion of a “spiral curriculum” embodies Bruner’s ideas by “spiraling” through similar topics at every age, but consistent with the child’s stage of thought.
• His spiral curriculum revisits basic ideas repeatedly, building upon them into more complex, abstract concepts over time in a developmentally appropriate sequence.
• The aim of education should be to create autonomous learners (i.e., learning to learn).
• Cognitive growth involves an interaction between basic human capabilities and “culturally invented technologies that serve as amplifiers of these capabilities.”
• These culturally invented technologies include not just obvious things such as computers and television, but also more abstract notions such as the way a culture categorizes phenomena, and language itself.
• Bruner would likely agree with  Vygotsky  that language serves to mediate between environmental stimuli and the individual’s response.

Three Modes of Representation

Modes of representation are how information or knowledge is stored and encoded in memory.

Rather than neat age-related stages (like Piaget), the modes of representation are integrated and only loosely sequential as they “translate” into each other.

Bruner (1966) was concerned with how knowledge is represented and organized through different modes of thinking (or representation).

In his research on the cognitive development of children,  Jerome Bruner proposed three modes of representation:

• Enactive representation (action-based)
• Iconic representation (image-based)
• Symbolic representation (language-based)

Bruner’s constructivist theory suggests it is effective when faced with new material to follow a progression from enactive to iconic to symbolic representation; this holds true even for adult learners.

Bruner’s work also suggests that a learner even of a very young age is capable of learning any material so long as the instruction is organized appropriately, in sharp contrast to the beliefs of Piaget and other stage theorists.

Enactive Mode (0-1 year)

In the  enactive mode , knowledge is stored primarily in the form of motor responses. This mode is used within the first year of life (corresponding with Piaget’s sensorimotor stage ).

Thinking is based entirely on physical actions , and infants learn by doing, rather than by internal representation (or thinking).

It involves encoding physical action-based information and storing it in our memory. For example, in the form of movement as muscle memory, a baby might remember the action of shaking a rattle.

And this is not just limited to children. Many adults can perform a variety of motor tasks (typing, sewing a shirt, operating a lawn mower) that they would find difficult to describe in iconic (picture) or symbolic (word) form.

This mode continues later in many physical activities, such as learning to ride a bike.

Iconic Mode (1-6 years)

Information is stored as sensory images (icons), usually visual ones, like pictures in the mind. For some, this is conscious; others say they don’t experience it.

This may explain why, when we are learning a new subject, it is often helpful to have diagrams or illustrations to accompany the verbal information.

Thinking is also based on using other mental images (icons), such as hearing, smell or touch.

Symbolic Mode (7 years onwards)

This develops last. In the  symbolic stage , knowledge is stored primarily as language, mathematical symbols, or in other symbol systems.

This mode is acquired around six to seven years old (corresponding to Piaget’s concrete operational stage ).

In the symbolic stage, knowledge is stored primarily as words, mathematical symbols, or other symbol systems, such as music.

Symbols are flexible in that they can be manipulated, ordered, classified, etc., so the user isn’t constrained by actions or images (which have a fixed relation to that which they represent).

According to Bruner’s taxonomy, these differ from icons in that symbols are “arbitrary.” For example, the word “beauty” is an arbitrary designation for the idea of beauty in that the word itself is no more inherently beautiful than any other word.

The Importance of Language

Language is important for the increased ability to deal with abstract concepts.

Bruner argues that language can code stimuli and free an individual from the constraints of dealing only with appearances, to provide a more complex yet flexible cognition.

The use of words can aid the development of the concepts they represent and can remove the constraints of the “here & now” concept.

Bruner views the infant as an intelligent & active problem solver from birth, with intellectual abilities basically similar to those of the mature adult.

Educational Implications

Education should aim to create autonomous learners (i.e., learning to learn).

For Bruner (1961), the purpose of education is not to impart knowledge, but instead to facilitate a child’s thinking and problem-solving skills which can then be transferred to a range of situations. Specifically, education should also develop symbolic thinking in children.

In 1960 Bruner’s text, The Process of Education was published. The main premise of Bruner’s text was that students are active learners who construct their own knowledge.

Bruner (1960) opposed Piaget’s notion of readiness . He argued that schools waste time trying to match the complexity of subject material to a child’s cognitive stage of development.

This means students are held back by teachers as certain topics are deemed too difficult to understand and must be taught when the teacher believes the child has reached the appropriate stage of cognitive maturity .

The Spiral Curriculum

Bruner (1960) adopts a different view and believes a child (of any age) is capable of understanding complex information:

“We begin with the hypothesis that any subject can be taught effectively in some intellectually honest form to any child at any stage of development.” (p. 33)

Bruner (1960) explained how this was possible through the concept of the spiral curriculum. This involved information being structured so that complex ideas can be taught at a simplified level first, and then re-visited at more complex levels later on.

The underlying principle in this is that the student should review particular concepts at over and over again during their educative experience; each time building and their understanding and requiring more sophisticated cognitive strategies (and thus increase the sophistication of their understanding).

Therefore, subjects would be taught at levels of gradually increasing difficultly (hence the spiral analogy). Ideally, teaching his way should lead to children being able to solve problems by themselves.

Bruner argues that, as children age, they are capable of increasingly complex modes of representation (basically, ways of thinking) – and the spiral curriculum should be sensitive to this development;

• Initially, children learn better using an  enactive  mode of representation (i.e. they learn better through “doing things” such as physical and manual tasks) – for instance, the concept of addition might be first taught by asking the child to combine piles of beads and counting the results.
• As they grow older – and more familiar with subject content – pupils become more confident in using an  iconic  mode of representation; they are able to perform tasks by imagining concrete pictures in their heads. To continue the above example; as the child becomes more confident with addition, they should be able to imagine the beads in order to complete additions (without physically needing to manipulate the piles).
• Finally, students become capable of more abstract,  symbolic  modes of representation; without the need for either physical manipulation or mental imagery. Consequently, at this point, the student should have little problem with completing a series of written calculations; of numbers which are higher than is possible by “imagining beads”.

Discovery Learning Theory

Bruner (1960) developed the concept of Discovery Learning – arguing that students should “not be presented with the subject matter in its final form, but rather are required to organize it themselves…[requiring them] to discover for themselves relationships that exist among items of information”.

Bruner (1961) proposes that learners construct their own knowledge and do this by organizing and categorizing information using a coding system.

Bruner believed that the most effective way to develop a coding system is to discover it rather than being told by the teacher.

The concept of discovery learning implies that students construct their own knowledge for themselves (also known as a constructivist approach ).

The result is an extremely active form of learning, in which the students are always engaged in tasks, finding patterns or solving puzzles – and in which they constantly need to exercise their existing schemata , reorganizing and amending these concepts to address the challenges of the task.

The role of the teacher should not be to teach information by rote learning, but instead to facilitate the learning process. This means that a good teacher will design lessons that help students discover the relationship between bits of information.

To do this a teacher must give students the information they need, but without organizing for them. The use of the spiral curriculum can aid the process of discovery learning .

For example, in teaching a particular concept, the teacher should present the set of instances that will best help learners develop an appropriate model of the concept. The teacher should also model the inquiry process. Bruner would likely not contend that all learning should be through discovery.

For example, it seems pointless to have children “discover” the names of the U.S. Presidents, or important dates in history.

Bruner’s theory is probably clearest when illustrated with practical examples. The instinctive response of a teacher to the task of helping a primary-school child understand the concept of odd and even numbers, for instance, would be to explain the difference to them.

However, Bruner would argue that understanding of this concept would be much more genuine if the child discovered the difference for themselves; for instance, by playing a game in which they had to share various numbers of beads fairly between themselves and their friend.

Discovery is not just an instructional technique, but an important learning outcome in itself. Schools should help learners develop their own ability to find the “recurrent regularities” in their environment.

Bruner would likely not contend that all learning should be through discovery. For example, it seems pointless to have children “discover” the names of the U.S. Presidents, or important dates in history.

Scaffolding Theory

On the surface, Bruner’s emphasis on the learner discovering subject content for themselves seemingly absolves the teacher of a great deal of work.

In practice, however, his model requires the teacher to be actively involved in lessons; providing cognitive scaffolding which will facilitate learning on the part of the student.

On the one hand, this involves the selection and design of appropriate stimulus materials and activities which the student can understand and complete – however Bruner also advocates that the teacher should circulate the classroom and work with individual students, performing six core “functions” (Wood, Bruner and Ross: 1976):

• Recruitment : ensuring that the student is interested in the task, and understands what is required of them.
• Reducing degrees of freedom : helping the student make sense of the material by eliminating irrelevant directions and thus reducing the “trial and error” aspect of learning.
• Direction Maintenance : ensuring that the learner is on-task and interest is maintained – often by breaking the ultimate aim of the task into “sub-aims” which are more readily understood and achieved.
• Marking critical features : highlighting relevant concepts or processes and pointing out errors.
• Frustration Control : stopping students from “giving up” on the task.
• Demonstration : providing models for imitation or possible (partial solution).

In this context, Bruner’s model might be better described as guided discovery learning; as the teacher is vital in ensuring that the acquisition of new concepts and processes is successful.

Bruner and Vygotsky

Both Bruner and Vygotsky emphasize a child’s environment, especially the social environment, more than Piaget did. Both agree that adults should play an active role in assisting the child’s learning.

Bruner, like Vygotsky, emphasized the social nature of learning, citing that other people should help a child develop skills through the process of scaffolding.

“[Scaffolding] refers to the steps taken to reduce the degrees of freedom in carrying out some task so that the child can concentrate on the difficult skill she is in the process of acquiring” (Bruner, 1978, p. 19).

He was especially interested in the characteristics of people whom he considered to have achieved their potential as individuals.

The term scaffolding first appeared in the literature when Wood, Bruner, and Ross described how tutors” interacted with a preschooler to help them solve a block reconstruction problem (Wood et al., 1976).

The concept of scaffolding is very similar to Vygotsky’s notion of the zone of proximal development , and it’s not uncommon for the terms to be used interchangeably.

Scaffolding involves helpful, structured interaction between an adult and a child with the aim of helping the child achieve a specific goal.

The purpose of the support is to allow the child to achieve higher levels of development by:

• Simplifying the task or idea.
• Motivating and encouraging the child.
• Highlighting important task elements or errors.
• Giving models that can be imitated.

Bruner and Piaget

There are similarities between Piaget and Bruner, but a significant difference is that Bruner’s modes are not related in terms of which presuppose the one that precedes it. While sometimes one mode may dominate in usage, they coexist.

Bruner states that the level of intellectual development determines the extent to which the child has been given appropriate instruction together with practice or experience.

So – the right way of presentation and explanation will enable a child to grasp a concept usually only understood by an adult. His theory stresses the role of education and the adult.

Although Bruner proposes stages of cognitive development, he doesn’t see them as representing different separate modes of thought at different points of development (like Piaget).

Instead, he sees a gradual development of cognitive skills and techniques into more integrated “adult” cognitive techniques.

Bruner views symbolic representation as crucial for cognitive development, and since language is our primary means of symbolizing the world, he attaches great importance to language in determining cognitive development.

• Children are innately PRE-ADAPTED to learning
• Children have a NATURAL CURIOSITY
• Children’s COGNITIVE STRUCTURES develop over time
• Children are ACTIVE participants in the learning process
• Cognitive development entails the acquisition of SYMBOLS
• Social factors, particularly language, were important for cognitive growth. These underpin the concept of ‘scaffolding’.
• The development of LANGUAGE is a cause not a consequence of cognitive development
• You can SPEED-UP cognitive development. You don’t have to wait for the child to be ready
• The involvement of ADULTS and MORE KNOWLEDGEABLE PEERS makes a big difference

Bruner, J. S. (1957). Going beyond the information given. New York: Norton.

Bruner, J. S. (1960). The Process of education. Cambridge, Mass.: Harvard University Press.

Bruner, J. S. (1961). The act of discovery. Harvard Educational Review , 31, 21-32.

Bruner, J. S. (1966). Toward a theory of instruction , Cambridge, Mass.: Belkapp Press.

Bruner, J. S. (1973). The relevance of education . New York: Norton.

Bruner, J. S. (1978). The role of dialogue in language acquisition. In A. Sinclair, R., J. Jarvelle, and W. J.M. Levelt (eds.) The Child’s Concept of Language. New York: Springer-Verlag.

Wood, D. J., Bruner, J. S., & Ross, G. (1976). The role of tutoring in problem solving. Journal of Child Psychiatry and Psychology , 17(2), 89-100.

Related Articles

Child Psychology

Vygotsky vs. Piaget: A Paradigm Shift

Interactional Synchrony

Internal Working Models of Attachment

Learning Theory of Attachment

Stages of Attachment Identified by John Bowlby And Schaffer & Emerson (1964)

Child Psychology , Personality

How Anxious Ambivalent Attachment Develops in Children

The Circle Of Fifths: A Complete Guide

Written by Samuel Chase

Last updated 19th April 2024

The Circle of Fifths is an incredible tool that has many different uses when it comes to music theory. It can help us with everything from knowing what chord progressions will sound good together to knowing what sharps or flats a key signature has.

In this post, I’m going to give you an overview of this useful musical concept and explain some of the ways that it can help you learn music theory.

Table of Contents

What is the Circle of Fifths?

As the name implies, the Circle of Fifths is a circle that connects all 12 tones used in Western music.

It is a visual representation of the musical relationship between these 12 tones. By using the Circle of Fifths, you can quickly and easily determine the key signature of any major or minor key, as well as the chords that will sound good together in a given key.

This makes it an essential tool for anyone learning music theory or for musicians who want to better understand the underlying structure of the music they play.

Building the Circle

To build the circle of fifths, we place all twelve note letter names around a circle like a clock.

But, rather than putting them in order from A – G, each of the notes is separated by intervals of perfect 5ths.

We start with the note C at the top of the circle (where 12 would be on a clock face).

We then add the next note in the circle by adding a note to the right of C (where one would be on a clock face) that is an interval of a perfect 5th above C.

Going up a perfect 5th from C, we reach G, and we carry on clockwise around the circle, adding the note a perfect 5th above.

Up a perfect 5th from G we reach D, then A, then E, then B, then F#.

We could carry on going up perfect 5ths from F# to C# and then C# to G# but there is an easier way.

We can go back to the C at the top in the middle and this time go down a perfect 5th and write notes in to the left of C.

To work out what note is a perfect 5th below C we can go down 7 semitones (half steps).

Seven semitones (half steps) down from C is F, so we can add the note F next to C (11 on a clock face).

We can then continue adding each note a perfect 5th below the previous note.

A perfect 5th below F is Bb, Bb to Eb, Eb to Ab, Ab to Db, and finally from Db to Gb.

F# and Gb are what we call enharmonic equivalents , which is just a fancy way of saying they’re the same but with different names. So you’ll often see both notes at the bottom of the circle of fifths.

How to Memorize the Circle of Fifths

Now that we’ve built a circle, we have to remember it rather than just memorize it through sheer repetition.

We can do this in a few ways.

The best way is through a mnemonic device – we create a sentence with the first letter of each word starting with a new note in the circle. 

For example, C harles G oes D ancing A t E very B ig F un C elebration. 

The first letter of every word (C – G – D – A – E – B – F – C) follows the Circle of Fifths, starting at the top C and going right (the last two notes here are technically F# and C#, remember).

This also represents the order of key signatures that have sharps (#) in them – C has 0 sharps, G has 1 sharp, D has 2, etc. all the way to C#, which has 7 sharps.

Starting at C and going the other way (to the left), we have the mnemonic example: C harles F alls B ehind E veryone A t D isc G olf C ourses.

Going this way, we have the notes C, F, Bb, Eb, Ab, Db, Gb, and Cb, which are also in order of how many flats they have in their key signatures: C has 0, F has 1 flat, Bb has 2, … and Cb has 7 flats.

However, as shown in the picture above, some of these keys are enharmonic equivalents. 

Cb = B, Gb = F#, and Db = C#.

This is something to look out for when memorizing the mnemonic sentences.

How to Use the Circle of Fifths

The circle of fifths has a number of very handy uses. Now I’ll cover a few of the things we can use it for.

Working Out Key Signatures

Just like we noticed in the two sentences above, the farther you go down on the right side of the clock, the more sharps you have in a key, and the farther you go down on the left side the more flats you have.

The top of the Circle has 0 flats or sharps – C Major.

Going down the right side, you gain one sharp to your key signature every note for the first seven notes (you can only have at max 7 sharps or flats in any key signature).

Going down the left side, you gain one flat to your key signature for the first seven notes. 

Working Out the Relative Major and Minor Keys

If you’re in any key, you can use the Circle of Fifths to figure out the relative major or minor of that key.

If you start in a major key, to find the relative minor key you go to the right three spaces in the circle.

For example, if your key is C major, you go right three spaces (C – G – D – A ) to get A, so the relative minor of C major is A minor.

If you’re in E major, your relative minor is C# minor; if you’re in Ab major, your relative minor is F minor.

And vice versa, if you’re in a minor key and want to find out the relative major, just go to the left three spaces.

For example, C minor to the left for three spaces (C – F – Bb – Eb) is Eb major.

If you’re in B minor, the relative major is D major; the relative major for Ab minor is Cb major.

See if you can write out the relative major and minor of each key.

Chords to Use in a Song

These days, most modern pop songs tend to use four chords to make their harmonies and melodies.

These four chords are easy to find on the circle of fifths.

In a major key, you start with the key that you’re in (for example, A major).

Then, you also use the relative minor (3 spaces to the right).

In A major, this would be F# minor.

Then, you add the keys on either side of your main key (one space to the right and left).

So in A major, you would then get D major and E major.

And there are your four chords: A major, D major, E major, and F# mino.

In C major, your four chords for a song are: C major, F major, G major and A minor.

You’ll now be able to play a lot of different songs. This video by the comedy musical act Axis Of Awesome demonstrates how great these four chords are. (Warning: contains some bad language).

Try figuring out the pop chords for all of the other keys!

Other Interesting Uses

There are some other interesting ways we can use the circle of fifths.

For example, if you move two spaces to the right, you have stepped up one whole tone. E.g., from C, two to the right gets you D, which is a whole tone above C.

From this, you can make the whole tone scale – just go two spaces to the right each time: C – (skip G) – D – (skip A) – E – F# – Ab – Bb – C .

Another cool feature is you can figure out what a tritone interval is for each note.

A tritone is six semitones (half steps) away from a note.

To figure this out using the circle of fifths, just take any note (e.g., Db) and go directly opposite that note on the circle (or move over six spaces).

The note opposite Db is G, so G-Db is a tritone interval.

The C at the top of the clock is opposite the F#/Gb at the bottom of the clock, so C-F# is a tritone.

That’s all for the Circle of Fifths!

There is a lot of cool stuff to learn and understand about its uses, so take your time, write it out yourself on a piece of paper, and see all of the interesting relationships between the notes and chords for yourself.

This is one of the most fundamental and helpful tools in all of music theory, and it basically defines harmonic progressions for most contemporary music like pop, rock and jazz.

We hope you were able to learn something about the circle of fifths.

Samuel Chase

Samuel Chase has been playing music since he was 5 years old, and teaching music since he was 13. He has a PhD in Music from the University of Surrey, and he has composed music that has been played in three different countries. He is currently working as a film composer and writing a book on film music.

Your Next Read

What Is Twelve-Tone Technique In Music: A Complete Guide

What Is The Musical Term For Fast?

10 Famous Examples Of Canons In Music

Signup for our Music Term of the Day Email and Expand Your Musical Vocabulary

Get In Touch

Hello Music Theory, Victoria Road, Godalming, Surrey, UK. GU7 1JR

[email protected]

+44 1483 974962

Popular Guides

Learn Music Theory

Types Of Music Notes

Guide To Scales

Modes In Music

Study Guides

Practice Papers

Video Courses

Company Info

Privacy Policy

Refund Policy

Terms Of Use

© Hello Music Theory 2024 |  Sitemap

Localization of Triangulated Categories with Respect to Extension-Closed Subcategories

• Published: 31 May 2024

Cite this article

• Yasuaki Ogawa 1  

35 Accesses

Explore all metrics

The aim of this paper is to develop a framework for localization theory of triangulated categories \(\mathcal {C}\) , that is, from a given extension-closed subcategory \(\mathcal {N}\) of \(\mathcal {C}\) , we construct a natural extriangulated structure on \(\mathcal {C}\) together with an exact functor \(Q:\mathcal {C}\rightarrow \widetilde{\mathcal {C}}_\mathcal {N}\) satisfying a suitable universality, which unifies several phenomena. Precisely, a given subcategory \(\mathcal {N}\) is thick if and only if the localization \(\widetilde{\mathcal {C}}_\mathcal {N}\) corresponds to a triangulated category. In this case, Q is nothing other than the usual Verdier quotient. Furthermore, it is revealed that \(\widetilde{\mathcal {C}}_\mathcal {N}\) is an exact category if and only if \(\mathcal {N}\) satisfies a generating condition \(\textsf{Cone}(\mathcal {N},\mathcal {N})=\mathcal {C}\) . Such an (abelian) exact localization \(\widetilde{\mathcal {C}}_\mathcal {N}\) provides a good understanding of some cohomological functors \(\mathcal {C}\rightarrow \textsf{Ab}\) , e.g., the heart of t -structures on \(\mathcal {C}\) and the abelian quotient of \(\mathcal {C}\) by a cluster-tilting subcategory \(\mathcal {N}\) .

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price excludes VAT (USA) Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Applications of Cotorsion Pairs on Triangulated Categories

Abelian categories arising from cluster tilting subcategories, abelian categories from triangulated categories via nakaoka–palu’s localization, availability of data and materials.

No data, models, or code were generated or used during the study.

Abe, N., Nakaoka, H.: General heart construction on a triangulated category (II): Associated homological functor. Appl. Categ. Structures 20 (2), 161–174 (2012)

Article   MathSciNet   Google Scholar  

Auslander, M., Solberg, Ø.: Relative homology and representation theory. I. Relative homology and homologically finite subcategories. Comm. Algebra 21 (9), 2995–3031 (1993)

Beilinson, A., Bernstein, J., Deligne, P.: Faisceaux Pervers (Perverse sheaves). Analysis and Topology on Singular Spaces, I, Luminy, 1981, Asterisque 100 5–171 (1982) (in French)

Beligiannis, A.: Relative homological algebra and purity in triangulated categories. J. Algebra 227 (1), 268–361 (2000)

Beligiannis, A.: Rigid objects, triangulated subfactors and abelian localizations. Math. Z. 274 (3–4), 841–883 (2013)

Bennett-Tennenhaus, R., Haugland, J., Sandøy, M.H., Shah, A.: The category of extensions and a characterisation of \(n\) -exangulated functors. Math. Z. 305 (3), 44 (2023)

Bennett-Tennenhaus, R., Shah, A.: Transport of structure in higher homological algebra. J. Algebra 574 , 514–549 (2021)

Buan, A.B., Marsh, B.R.: From triangulated categories to module categories via localisation. Trans. Amer. Math. Soc. 365 (6), 2845–2861 (2013)

Buan, A.B.,x Marsh, B.R.: From triangulated categories to module categories via localization II: calculus of fractions. J. Lond. Math. Soc. (2). 86 (1), 152–170 (2012)

Cárdenas-Escudero, M.E.: Localization for exact categories. ProQuest LLC, Ann Arbor, MI, 1998. Thesis (Ph.D.)–State University of New York at Binghamton

Dräxler, P., Reiten, I., Smalø, S., Solberg, Ø.: Exact categories and vector space categories. With an appendix by B. Keller. Trans. Amer. Math. Soc. 351 (2), 647–682 (1999)

Enomoto, H.: Classifying substructures of extriangulated categories via Serre subcategories. Appl. Categ. Structures 29 (6), 1005–1018 (2021)

Fritz, T.: Categories of Fractions Revisited. Morfismos 15 (2), 19–38 (2011)

Google Scholar  

Gabriel, P.: Des catégories abéliennes. Bull. Soc. Math. France 90 , 323–448 (1962)

Gabriel, P., Zisman, M.: Calculus of fractions and homotopy theory. Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 35 Springer-Verlag New York, Inc., New York x+168 pp. (1967)

Grimeland, B., Jacobsen, K.: Abelian quotients of triangulated categories. J. Algebra 439 , 110–133 (2015)

Happel, D.: Triangulated categories in the representation theory of finite dimensional algebras. London Mathematical Society Lecture Note Series, 119. Cambridge University Press, Cambridge (1988)

Haugland, J.: The Grothendieck group of an \(n\) -exangulated category. Appl. Categ. Structures 29 (3), 431–446 (2021)

Herschend, M., Liu, Y., Nakaoka, H.: \(n\) -exangulated categories (I): Definitions and fundamental properties. J. Algebra 570 , 531–586 (2021)

Hassoun, S., Shah, A.: Integral and quasi-abelian hearts of twin cotorsion pairs on extriangulated categories. Comm. Algebra 48 (12), 5142–5162 (2020)

Iyama, O., Nakaoka, H., Palu, Y.: Auslander-Reiten theory in extriangulated categories. Trans. Amer. Math. Soc. Ser. B 11 , 248–305 (2024)

Jørgensen, P., Palu, Y.: A Caldero-Chapoton map for infinite clusters. Trans. Amer. Math. Soc. 365 (3), 1125–1147 (2013)

Jørgensen, P., Shah, A.: The Index With Respect to a Rigid Subcategory of a Triangulated Category. Int. Math. Res. Not. IMRN 4 , 3278–3309 (2024)

Keller, B.,x Reiten, I.: Cluster-tilted algebras are Gorenstein and stably Calabi-Yau. Adv. Math. 211 (1), 123–151 (2007)

Klapproth, C.: \(n\) -extension closed subcategories of \(n\) -exangulated categories. arXiv:2209.01128v3

Koenig, S., Zhu, B.: From triangulated categories to abelian categories: cluster tilting in a general framework. Math. Z. 258 (1), 143–160 (2008)

Krause, H.: Smashing subcategories and the telescope conjecture-an algebraic approach. Invent. Math. 139 (1), 99–133 (2000)

Liu, Y.: Localizations of the hearts of cotorsion pairs associated with mutations. Glasg. Math. J. 62 (3), 564–583 (2020)

Liu, Y., Nakaoka, H.: Hearts of twin cotorsion pairs on extriangulated categories. J. Algebra 528 , 96–149 (2019)

Liu, Y., Zhou, P.: Abelian categories arising from cluster tilting subcategories II: quotient functors. Proc. Roy. Soc. Edinburgh Sect. A 150 (6), 2721–2756 (2020)

Nakaoka, H.: General heart construction on a triangulated category (I): Unifying \(t\) -structures and cluster tilting subcategories. Appl. Categ. Structures 19 (6), 879–899 (2011)

Nakaoka, H.: General heart construction for twin torsion pairs on triangulated categories. J. Algebra 374 , 195–215 (2013)

Nakaoka, H., Ogawa, Y., Sakai, A.: Localization of extriangulated categories. J. Algebra 611 , 341–398 (2022)

Nakaoka, H., Palu, Y.: Extriangulated categories, Hovey twin cotorsion pairs and model structures. Cah. Topol. Géom. Différ. Catég. 60 (2), 117–193 (2019)

MathSciNet   Google Scholar  

Neeman, A.: Triangulated categories. Annals of Mathematics Studies 148, Princeton University Press (2001)

Ogawa, Y.: Auslander’s defects over extriangulated categories: an application for the general heart construction. J. Math. Soc. Japan 73 (4), 1063–1089 (2021)

Ogawa, Y.: Abelian Categories from Triangulated Categories via Nakaoka-Palu’s Localization. Appl. Categ. Structures 30 (4), 611–639 (2022)

Padrol, A., Palu, Y., Pilaud, V., Plamondon, P.-G.: Associahedra for finite-type cluster algebras and minimal relations between \( {g}\) -vectors. Proc. Lond. Math. Soc. 127 (3), 513–588 (2023)

Palu, Y.: Cluster characters for 2-Calabi-Yau triangulated categories. Ann. Inst. Fourier (Grenoble) 58 (6), 2221–2248 (2008)

Rump, W.: Almost abelian categories. Topologie Géom. Différentielle Catég. 42 (3), 163–225 (2001)

Rump, W.: The acyclic closure of an exact category and its triangulation. J. Algebra 565 , 402–440 (2021)

Sakai, A.: Relative extriangulated categories arising from half exact functors. J. Algebra 614 , 592–610 (2023)

Salce, L.: Cotorsion theories for abelian groups in Symposia Mathematica, Vol. XXIII (Conf. Abelian Groups and their Relationship to the Theory of Modules, INDAM, Rome, 1977) (1979), 11–32

Tattar, A.: The Structure of Aisles and Co-aisles of t-Structures and Co-t-structures. Appl. Categ. Structures 32 (1), 5 (2024)

Verdier, J.-L.: Des catégories dérivées des catégories abéliennes. Astérisque, 239:xii+253,: 1996. With a preface by Luc Illusie, Edited and with a note by Georges Maltsiniotis (1997)

Download references

Acknowledgements

The author is grateful for Hiroyuki Nakaoka, Arashi Sakai an Shunya Saito for their interest and valuable comments. He also would like to show his gratitude to the anonymous referee who found and corrected a mistake in the preliminary version. This work is supported by JSPS KAKENHI Grant Number JP22K13893.

No funding was received to assist with the preparation of this manuscript.

Author information

Authors and affiliations.

Faculty of Engineering Science, Kansai University, 3 Chome-3-35 Yamatecho, Suita Osaka, 564-8680, Japan

Yasuaki Ogawa

You can also search for this author in PubMed   Google Scholar

Contributions

Y. Ogawa wrote the all manuscript text.

Corresponding author

Correspondence to Yasuaki Ogawa .

Ethics declarations

Ethical approval.

Not applicable, because this article does not contain any studies with human or animal subjects.

Competing interests

The authors declare no competing interests.

Additional information

Presented by: Karin Baur

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Ogawa, Y. Localization of Triangulated Categories with Respect to Extension-Closed Subcategories. Algebr Represent Theor (2024). https://doi.org/10.1007/s10468-024-10272-y

Download citation

Received : 26 May 2023

Accepted : 21 April 2024

Published : 31 May 2024

DOI : https://doi.org/10.1007/s10468-024-10272-y

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Verdier localization
• Triangulated category
• Extriangulated category
• t -structure
• Cotorsion pair

Mathematics Subject Classification (2010)

• Primary: 18G80
• Secondary: 18E10
• Find a journal
• Publish with us
• Track your research