type 2 error hypothesis testing meaning

Type 1 and Type 2 Errors in Statistics

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

On This Page:

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty). Because a p -value is based on probabilities, there is always a chance of making an incorrect conclusion regarding accepting or rejecting the null hypothesis ( H 0 ).

Anytime we make a decision using statistics, there are four possible outcomes, with two representing correct decisions and two representing errors.

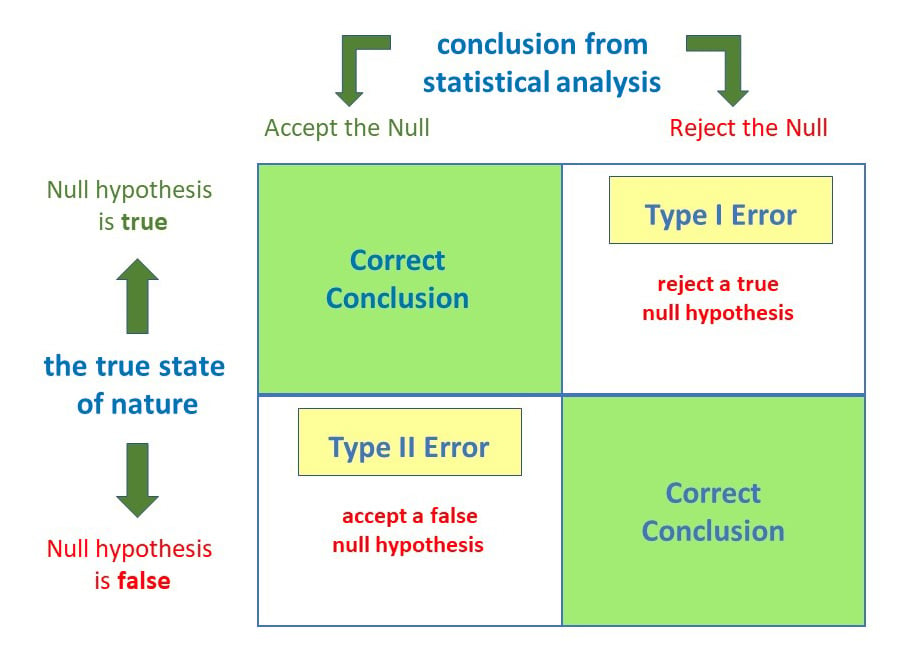
The chances of committing these two types of errors are inversely proportional: that is, decreasing type I error rate increases type II error rate and vice versa.

As the significance level (α) increases, it becomes easier to reject the null hypothesis, decreasing the chance of missing a real effect (Type II error, β). If the significance level (α) goes down, it becomes harder to reject the null hypothesis , increasing the chance of missing an effect while reducing the risk of falsely finding one (Type I error).

Type I error 

A type 1 error is also known as a false positive and occurs when a researcher incorrectly rejects a true null hypothesis. Simply put, it’s a false alarm.

This means that you report that your findings are significant when they have occurred by chance.

The probability of making a type 1 error is represented by your alpha level (α), the p- value below which you reject the null hypothesis.

A p -value of 0.05 indicates that you are willing to accept a 5% chance of getting the observed data (or something more extreme) when the null hypothesis is true.

You can reduce your risk of committing a type 1 error by setting a lower alpha level (like α = 0.01). For example, a p-value of 0.01 would mean there is a 1% chance of committing a Type I error.

However, using a lower value for alpha means that you will be less likely to detect a true difference if one really exists (thus risking a type II error).

Scenario: Drug Efficacy Study

Imagine a pharmaceutical company is testing a new drug, named “MediCure”, to determine if it’s more effective than a placebo at reducing fever. They experimented with two groups: one receives MediCure, and the other received a placebo.

• Null Hypothesis (H0) : MediCure is no more effective at reducing fever than the placebo.
• Alternative Hypothesis (H1) : MediCure is more effective at reducing fever than the placebo.

After conducting the study and analyzing the results, the researchers found a p-value of 0.04.

If they use an alpha (α) level of 0.05, this p-value is considered statistically significant, leading them to reject the null hypothesis and conclude that MediCure is more effective than the placebo.

However, MediCure has no actual effect, and the observed difference was due to random variation or some other confounding factor. In this case, the researchers have incorrectly rejected a true null hypothesis.

Error : The researchers have made a Type 1 error by concluding that MediCure is more effective when it isn’t.

Implications

Resource Allocation : Making a Type I error can lead to wastage of resources. If a business believes a new strategy is effective when it’s not (based on a Type I error), they might allocate significant financial and human resources toward that ineffective strategy.

Unnecessary Interventions : In medical trials, a Type I error might lead to the belief that a new treatment is effective when it isn’t. As a result, patients might undergo unnecessary treatments, risking potential side effects without any benefit.

Reputation and Credibility : For researchers, making repeated Type I errors can harm their professional reputation. If they frequently claim groundbreaking results that are later refuted, their credibility in the scientific community might diminish.

Type II error

A type 2 error (or false negative) happens when you accept the null hypothesis when it should actually be rejected.

Here, a researcher concludes there is not a significant effect when actually there really is.

The probability of making a type II error is called Beta (β), which is related to the power of the statistical test (power = 1- β). You can decrease your risk of committing a type II error by ensuring your test has enough power.

You can do this by ensuring your sample size is large enough to detect a practical difference when one truly exists.

Scenario: Efficacy of a New Teaching Method

Educational psychologists are investigating the potential benefits of a new interactive teaching method, named “EduInteract”, which utilizes virtual reality (VR) technology to teach history to middle school students.

They hypothesize that this method will lead to better retention and understanding compared to the traditional textbook-based approach.

• Null Hypothesis (H0) : The EduInteract VR teaching method does not result in significantly better retention and understanding of history content than the traditional textbook method.
• Alternative Hypothesis (H1) : The EduInteract VR teaching method results in significantly better retention and understanding of history content than the traditional textbook method.

The researchers designed an experiment where one group of students learns a history module using the EduInteract VR method, while a control group learns the same module using a traditional textbook.

After a week, the student’s retention and understanding are tested using a standardized assessment.

Upon analyzing the results, the psychologists found a p-value of 0.06. Using an alpha (α) level of 0.05, this p-value isn’t statistically significant.

Therefore, they fail to reject the null hypothesis and conclude that the EduInteract VR method isn’t more effective than the traditional textbook approach.

However, let’s assume that in the real world, the EduInteract VR truly enhances retention and understanding, but the study failed to detect this benefit due to reasons like small sample size, variability in students’ prior knowledge, or perhaps the assessment wasn’t sensitive enough to detect the nuances of VR-based learning.

Error : By concluding that the EduInteract VR method isn’t more effective than the traditional method when it is, the researchers have made a Type 2 error.

This could prevent schools from adopting a potentially superior teaching method that might benefit students’ learning experiences.

Missed Opportunities : A Type II error can lead to missed opportunities for improvement or innovation. For example, in education, if a more effective teaching method is overlooked because of a Type II error, students might miss out on a better learning experience.

Potential Risks : In healthcare, a Type II error might mean overlooking a harmful side effect of a medication because the research didn’t detect its harmful impacts. As a result, patients might continue using a harmful treatment.

Stagnation : In the business world, making a Type II error can result in continued investment in outdated or less efficient methods. This can lead to stagnation and the inability to compete effectively in the marketplace.

How do Type I and Type II errors relate to psychological research and experiments?

Type I errors are like false alarms, while Type II errors are like missed opportunities. Both errors can impact the validity and reliability of psychological findings, so researchers strive to minimize them to draw accurate conclusions from their studies.

How does sample size influence the likelihood of Type I and Type II errors in psychological research?

Sample size in psychological research influences the likelihood of Type I and Type II errors. A larger sample size reduces the chances of Type I errors, which means researchers are less likely to mistakenly find a significant effect when there isn’t one.

A larger sample size also increases the chances of detecting true effects, reducing the likelihood of Type II errors.

Are there any ethical implications associated with Type I and Type II errors in psychological research?

Yes, there are ethical implications associated with Type I and Type II errors in psychological research.

Type I errors may lead to false positive findings, resulting in misleading conclusions and potentially wasting resources on ineffective interventions. This can harm individuals who are falsely diagnosed or receive unnecessary treatments.

Type II errors, on the other hand, may result in missed opportunities to identify important effects or relationships, leading to a lack of appropriate interventions or support. This can also have negative consequences for individuals who genuinely require assistance.

Therefore, minimizing these errors is crucial for ethical research and ensuring the well-being of participants.

Further Information

• Publication manual of the American Psychological Association
• Statistics for Psychology Book Download

• Search Search Please fill out this field.

What Is a Type II Error?

• How It Works
• Type I vs. Type II Error

The Bottom Line

• Corporate Finance
• Financial Analysis

Type II Error: Definition, Example, vs. Type I Error

Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.

Michela Buttignol / Investopedia

A type II error is a statistical term used within the context of hypothesis testing that describes the error that occurs when one fails to reject a null hypothesis that is actually false. A type II error produces a false negative, also known as an error of omission.

For example, a test for a disease may report a negative result when the patient is infected. This is a type II error because we accept the conclusion of the test as negative, even though it is incorrect.

A type II error can be contrasted with a type I error , where researchers incorrectly reject a true null hypothesis. A type II error happens when one fails to reject a null hypothesis that is actually false. A type I error produces a false positive.

Key Takeaways

• A type II error is defined as the probability of incorrectly failing to reject the null hypothesis, when in fact it is not applicable to the entire population.
• A type II error is essentially a false negative.
• A type II error can be made less likely by making more stringent criteria for rejecting a null hypothesis, although this increases the chances of a false positive.
• The sample size, the true population size, and the preset alpha level influence the magnitude of risk of an error.
• Analysts need to weigh the likelihood and impact of type II errors with type I errors.

Understanding a Type II Error

A type II error, also known as an error of the second kind or a beta error, confirms an idea that should have been rejected—for instance, claiming that two observances are the same, despite them being different. A type II error does not reject the null hypothesis, even though the alternative hypothesis is actually correct. In other words, a false finding is accepted as true.

The likelihood of a type II error can be reduced by making more stringent criteria for rejecting a null hypothesis (H 0 ). For example, if an analyst is considering anything that falls within the +/- bounds of a 95% confidence interval as statistically insignificant (a negative result), then by decreasing that tolerance to +/- 90%, and subsequently narrowing the bounds, you will get fewer negative results, and thus reduce the chances of a false negative.

Taking these steps, however, tends to increase the chances of encountering a type I error—a false-positive result. When conducting a hypothesis test, the probability or risk of making a type I error or type II error should be considered.

The steps taken to reduce the chances of encountering a type II error tend to increase the probability of a type I error.

Type I Errors vs. Type II Errors

The difference between a type II error and a type I error is that a type I error rejects the null hypothesis when it is true (i.e., a false positive). The probability of committing a type I error is equal to the level of significance that was set for the hypothesis test. Therefore, if the level of significance is 0.05, there is a 5% chance that a type I error may occur.

The probability of committing a type II error is equal to one minus the power of the test, also known as beta. The power of the test could be increased by increasing the sample size, which decreases the risk of committing a type II error.

Some statistical literature will include overall significance level and type II error risk as part of the report’s analysis. For example, a 2021 meta-analysis of exosome in the treatment of spinal cord injury recorded an overall significance level of 0.05 and a type II error risk of 0.1.

Example of a Type II Error

Assume a biotechnology company wants to compare how effective two of its drugs are for treating diabetes. The null hypothesis states the two medications are equally effective. A null hypothesis, H 0 , is the claim that the company hopes to reject using the one-tailed test . The alternative hypothesis, H a , states that the two drugs are not equally effective. The alternative hypothesis, H a , is the state of nature that is supported by rejecting the null hypothesis.

The biotech company implements a large clinical trial of 3,000 patients with diabetes to compare the treatments. The company randomly divides the 3,000 patients into two equally sized groups, giving one group one of the treatments and the other group the other treatment. It selects a significance level of 0.05, which indicates it is willing to accept a 5% chance it may reject the null hypothesis when it is true or a 5% chance of committing a type I error.

Assume the beta is calculated to be 0.025, or 2.5%. Therefore, the probability of committing a type II error is 97.5%. If the two medications are not equal, the null hypothesis should be rejected. However, if the biotech company does not reject the null hypothesis when the drugs are not equally effective, then a type II error occurs.

What Is the Difference Between Type I and Type II Errors?

A type I error occurs if a null hypothesis is rejected that is actually true in the population. This type of error is representative of a false positive. Alternatively, a type II error occurs if a null hypothesis is not rejected that is actually false in the population. This type of error is representative of a false negative.

What Causes Type II Errors?

A type II error is commonly caused if the statistical power of a test is too low. The higher the statistical power, the greater the chance of avoiding an error. It’s often recommended that the statistical power should be set to at least 80% prior to conducting any testing.

What Factors Influence the Magnitude of Risk for Type II Errors?

As the sample size of a study increases, the risk of type II errors should decrease. As the true population effect size increases, the probability of a type II error should also decrease. Finally, the preset alpha level set by the research influences the magnitude of risk. As the alpha level set decreases, the risk of a type II error increases.

How Can a Type II Error Be Minimized?

It is not possible to fully prevent committing a type II error, but the risk can be minimized by increasing the sample size. However, doing so will also increase the risk of committing a type I error instead.

In statistics, a type II error results in a false negative—meaning that there is a finding, but it has been missed in the analysis (or that the null hypothesis is not rejected when it ought to have been). A type II error can occur if there is not enough power in statistical tests, often resulting from sample sizes that are too small. Increasing the sample size can help reduce the chances of committing a type II error.

Type II errors can be contrasted with type I errors, which are false positives.

Europe PMC. “ A Meta-Analysis of Exosome in the Treatment of Spinal Cord Injury .”

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6.1 - type i and type ii errors.

When conducting a hypothesis test there are two possible decisions: reject the null hypothesis or fail to reject the null hypothesis. You should remember though, hypothesis testing uses data from a sample to make an inference about a population. When conducting a hypothesis test we do not know the population parameters. In most cases, we don't know if our inference is correct or incorrect.

When we reject the null hypothesis there are two possibilities. There could really be a difference in the population, in which case we made a correct decision. Or, it is possible that there is not a difference in the population (i.e., \(H_0\) is true) but our sample was different from the hypothesized value due to random sampling variation. In that case we made an error. This is known as a Type I error.

When we fail to reject the null hypothesis there are also two possibilities. If the null hypothesis is really true, and there is not a difference in the population, then we made the correct decision. If there is a difference in the population, and we failed to reject it, then we made a Type II error.

Rejecting \(H_0\) when \(H_0\) is really true, denoted by \(\alpha\) ("alpha") and commonly set at .05

     \(\alpha=P(Type\;I\;error)\)

Failing to reject \(H_0\) when \(H_0\) is really false, denoted by \(\beta\) ("beta")

     \(\beta=P(Type\;II\;error)\)

Example: Trial Section  

A man goes to trial where he is being tried for the murder of his wife.

We can put it in a hypothesis testing framework. The hypotheses being tested are:

• \(H_0\) : Not Guilty
• \(H_a\) : Guilty

Type I error  is committed if we reject \(H_0\) when it is true. In other words, did not kill his wife but was found guilty and is punished for a crime he did not really commit.

Type II error  is committed if we fail to reject \(H_0\) when it is false. In other words, if the man did kill his wife but was found not guilty and was not punished.

Example: Culinary Arts Study Section  

A group of culinary arts students is comparing two methods for preparing asparagus: traditional steaming and a new frying method. They want to know if patrons of their school restaurant prefer their new frying method over the traditional steaming method. A sample of patrons are given asparagus prepared using each method and asked to select their preference. A statistical analysis is performed to determine if more than 50% of participants prefer the new frying method:

• \(H_{0}: p = .50\)
• \(H_{a}: p>.50\)

Type I error  occurs if they reject the null hypothesis and conclude that their new frying method is preferred when in reality is it not. This may occur if, by random sampling error, they happen to get a sample that prefers the new frying method more than the overall population does. If this does occur, the consequence is that the students will have an incorrect belief that their new method of frying asparagus is superior to the traditional method of steaming.

Type II error  occurs if they fail to reject the null hypothesis and conclude that their new method is not superior when in reality it is. If this does occur, the consequence is that the students will have an incorrect belief that their new method is not superior to the traditional method when in reality it is.

Course Outline

Type I and Type II Errors: Definition, Differences, Example

Type I and Type II Blunders are two sorts of mistakes that can happen in statistical hypothesis testing. A Type I blunder happens when we dismiss a genuine null hypothesis, whereas a Sort II mistake happens when we fail to dismiss a wrong null hypothesis. Understanding the contrast between these mistakes and how to play down them is basic in making exact and educated choices based on statistical examination.

In statistical hypothesis testing, we make decisions based on the data we observe. In any case, these choices are inclined to blunders. Type I and Type II mistakes are the two sorts of blunders that can happen in speculation testing. It is fundamental to get it these blunders to form the correct choices based on the statistical investigation.

Type I and Type II Errors

Definition of Type I Error

Type I error is a false positive result in hypothesis testing.It happens when we fail to dismiss the invalid speculation, even though it is wrong. In other words, we conclude that there's no noteworthy impact or difference when there's a genuine impact or distinction. The likelihood of making a Type II error is signified by the Greek letter beta (β) and depends on the test estimate, impact estimate, and centrality level.

Definition of Type II Error

Type II error is a false negative result in hypothesis testing. It occurs when we fail to reject the null hypothesis, even though it is false. In other words, we conclude that there is no significant effect or difference when there is a real effect or difference. The probability of making a Type II error is denoted by the Greek letter beta (β) and depends on the sample size, effect size, and significance level.

Type I and Type II Errors Graph

Example of Type I and Type II Errors:

Suppose a medical test is conducted to determine if a person is pregnant or not. The null hypothesis is that the person is not pregnant, and the alternative hypothesis is that the person is pregnant.

• Type I Error: This occurs when the test incorrectly rejects the null hypothesis (person is not pregnant) when it is actually true. In this case, a Type I error would mean that a person who is not pregnant is incorrectly identified as pregnant by the test. This could lead to unnecessary medical treatments or procedures.
• Type II Error: This occurs when the test incorrectly fails to reject the null hypothesis (person is not pregnant) when it is actually false (person is pregnant). In this case, a Type II error would mean that a person who is pregnant is incorrectly identified as not pregnant by the test. This could delay necessary medical treatments or procedures.

Both Type I and Type II errors can have serious consequences, and it's important for medical professionals to carefully consider the potential for error when interpreting test results.

Minimizing Type I and Type II Errors:

In hypothesis testing, we need to minimize both Type I and Type II mistakes. However, it isn't continuously conceivable to diminish both blunders at the same time. Assume we need to diminish the likelihood of a Sort I mistake (i.e., we want to be more conservative). In that case, ready to diminish the importance level (α), which can increment the likelihood of a Type II mistake. Alternately, in the event that we need to reduce the probability of a Sort II mistake (i.e., we need to be more delicate), ready to increment the test estimate or impact measure, which is able decrease the likelihood of a Type I error.

Relation to Power and Sample Size:

The power of a hypothesis test is the probability of rejecting the null hypothesis when it is false (i.e., not making a Type II error). Power is inversely related to the probability of making a Type II error (β). Increasing the sample size or effect size can increase the power of a hypothesis test. Additionally, increasing the significance level (α) can increase power, but it also increases the probability of making a Type I error.

Type I and Type II errors are crucial concepts in hypothesis testing. Type I errors occur when we reject the null hypothesis when it is true, and Type II errors occur when we fail to reject the null hypothesis when it is false. It is essential to minimize both types of errors and balance the significance level (α) and the sample size/effect size to achieve the desired level of power in hypothesis testing.

Key Takeaways

• Hypothesis testing is an important tool in statistics that helps us make decisions about the population based on sample data.
• Type I error occurs when we reject a null hypothesis that is actually true, while Type II error occurs when we fail to reject a null hypothesis that is actually false.
• The probability of Type I error is denoted by alpha, while the probability of Type II error is denoted by beta.
• The power of a test is the probability of correctly rejecting a false null hypothesis and is equal to 1 minus the probability of Type II error.
• The level of significance of a test is the maximum probability of Type I error that we are willing to accept, and it is usually set to 0.05 or 0.01.
• Type I and Type II errors are important considerations when interpreting the results of hypothesis tests and should be taken into account when making decisions based on statistical analysis.

1. What is a Type I error in hypothesis testing?  

A) Rejecting the null hypothesis when it is true 

B) Failing to reject the null hypothesis when it is false 

C) Rejecting the alternative hypothesis when it is true 

D) Failing to reject the alternative hypothesis when it is false Answer : A

2. What is a Type II error in hypothesis testing?  

D) Failing to reject the alternative hypothesis when it is false Answer : B

3. Which type of error is more serious in hypothesis testing?  

A) Type I error 

B) Type II error 

C) Both errors are equally serious 

D) It depends on the specific context and consequences of the error 

4. Which of the following can reduce the risk of both Type I and Type II errors?  

A) Increasing the sample size 

B) Decreasing the sample size 

C) Increasing the level of significance 

D) Decreasing the level of significance 

Top Tutorials

Related Articles

• [email protected]
• 08046008400
• Official Address
• 4th floor, 133/2, Janardhan Towers, Residency Road, Bengaluru, Karnataka, 560025
• Communication Address
• 4th floor, 315 Work Avenue, Siddhivinayak Tower, 152, 1st Cross Rd., 1st Block, Koramangala, Bengaluru, Karnataka, 560034

• Success Stories
• Hire From Us
• Certification in Full Stack Data Science and AI
• Certification in Full Stack Web Development
• MS in Computer Science: Artificial Intelligence and Machine Learning
• Placement Statistics
• Online Compilers
• Join AlmaBetter
• Become an Affiliate
• Become A Coach
• Coach Login
• Refer and Earn
• Privacy Statement
• Terms of Use

• Prompt Library
• DS/AI Trends
• Stats Tools
• Interview Questions
• Generative AI
• Machine Learning
• Deep Learning

Type I & Type II Errors in Hypothesis Testing: Examples

Table of Contents

What is a Type I Error?

When doing hypothesis testing, one ends up incorrectly rejecting the null hypothesis (default state of being) when in reality it holds true. The probability of rejecting a null hypothesis when it actually holds good is called as Type I error . Generally, a higher Type I error triggers eyebrows because this indicates that there is evidence against the default state of being. This essentially means that unexpected outcomes or alternate hypotheses can be true. Thus, it is recommended that one should aim to keep Type I errors as small as possible. Type I error is also called as “ false positive “.

Lets try and understand type I error with the help of person held guilty or otherwise given the fact that he is innocent. The claim made or the hypothesis is that the person has committed a crime or is guilty. The null hypothesis will be that the person is not guilty or innocent. Based on the evidence gathered, the null hypothesis that the person is not guilty gets rejected. This means that the person is held guilty. However, the rejection of null hypothesis is false. This means that the person is held guilty although he/she was not guilty. In other words, the innocent person is convicted. This is an example of Type I error.

In order to achieve the lower Type I error, the hypothesis testing assigns a fairly small value to the significance level. Common values for significance level are 0.05 and 0.01, although, on average scenarios, 0.05 is used. Mathematically speaking, if the significance level is set to be 0.05, it is acceptable/OK to falsely or incorrectly reject the Null Hypothesis for 5% of the time.

Type I Error & House on Fire

Whether the house is on fire?

Type I Error & Covid-19 Diagnosis

What is a Type II Error?

Type ii error & house on fire, type ii error & covid-19 diagnosis.

In the case of Covid-19 example, if the person having a breathing problem fails to reject the Null hypothesis , and does not go for Covid-19 diagnostic tests when he/she should actually have rejected it. This may prove fatal to life in case the person is actually suffering from Covid-19. Type II errors can turn out to be very fatal and expensive.

Type I Error & Type II Error Explained with Diagram

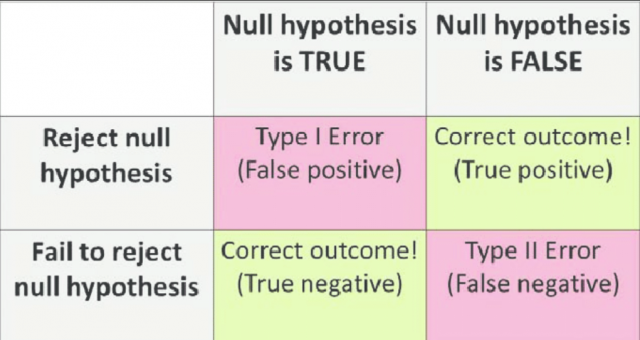
Given the diagram above, one could observe the following two scenarios:

• Type I Error : When one rejects the Null Hypothesis (H0 – Default state of being) given that H0 is true, one commits a Type I error. It can also be termed as false positive.
• Type II Error : When one fails to reject the Null hypothesis when it is actually false or does not hold good, one commits a Type II error. It can also be termed as a false negative.
• In other cases when one rejects the Null Hypothesis when it is false or not true, and when fails to reject the Null hypothesis when it is true is the correct decision .

Type I Error & Type II Error: Trade-off

Ideally it is desired that both the Type I and Type II error rates should remain small. But in practice, this is extermely hard to achieve. There typically is a trade-off. The Type I error can be made small by only rejecting H0 if we are quite sure that it doesn’t hold. This would mean a very small value of significance level such as 0.01. However, this will result in an increase in the Type II error. Alternatively, The Type II error can be made small by rejecting H0 in the presence of even modest evidence that it does not hold. This can be obtained by having slightly higher value of significance level ssuch as 0.1. This will, however, cause the Type I error to be large. In practice, we typically view Type I errors as “bad” or “not good” than Type II errors, because the former involves declaring a scientific finding that is not correct. Hence, when the hypothesis testing is performed, What is desired is typically a low Type I error rate — e.g., at most α = 0.05,  while trying to make the Type II error small (or, equivalently, the power large).

Understanding the difference between Type I and Type II errors can help you make more informed decisions about how to use statistics in your research. If you are looking for some resources on how to integrate these concepts into your own work, reach out to us. We would be happy to provide additional training or answer any questions that may arise!

Recent Posts

• Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
• LLMs for Adaptive Learning & Personalized Education - October 8, 2024
• Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024

Ajitesh Kumar

• Search for:

ChatGPT Prompts (250+)

• Generate Design Ideas for App
• Expand Feature Set of App
• Create a User Journey Map for App
• Generate Visual Design Ideas for App
• Generate a List of Competitors for App
• Agentic Reasoning Design Patterns in AI: Examples
• LLMs for Adaptive Learning & Personalized Education
• Sparse Mixture of Experts (MoE) Models: Examples
• Anxiety Disorder Detection & Machine Learning Techniques
• Confounder Features & Machine Learning Models: Examples

Data Science / AI Trends

• • Sentiment Analysis Real World Examples
• • Prepend any arxiv.org link with talk2 to load the paper into a responsive chat application
• • Custom LLM and AI Agents (RAG) On Structured + Unstructured Data - AI Brain For Your Organization
• • Guides, papers, lecture, notebooks and resources for prompt engineering
• • Common tricks to make LLMs efficient and stable

Free Online Tools

• Create Scatter Plots Online for your Excel Data
• Histogram / Frequency Distribution Creation Tool
• Online Pie Chart Maker Tool
• Z-test vs T-test Decision Tool
• Independent samples t-test calculator

Recent Comments

I found it very helpful. However the differences are not too understandable for me

Very Nice Explaination. Thankyiu very much,

in your case E respresent Member or Oraganization which include on e or more peers?

Such a informative post. Keep it up

Thank you....for your support. you given a good solution for me.

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Type I & Type II Errors | Differences, Examples, Visualizations

Type I & Type II Errors | Differences, Examples, Visualizations

Published on 18 January 2021 by Pritha Bhandari . Revised on 2 February 2023.

In statistics , a Type I error is a false positive conclusion, while a Type II error is a false negative conclusion.

Making a statistical decision always involves uncertainties, so the risks of making these errors are unavoidable in hypothesis testing .

The probability of making a Type I error is the significance level , or alpha (α), while the probability of making a Type II error is beta (β). These risks can be minimized through careful planning in your study design.

• Type I error (false positive) : the test result says you have coronavirus, but you actually don’t.
• Type II error (false negative) : the test result says you don’t have coronavirus, but you actually do.

Table of contents

Error in statistical decision-making, type i error, type ii error, trade-off between type i and type ii errors, is a type i or type ii error worse, frequently asked questions about type i and ii errors.

Using hypothesis testing, you can make decisions about whether your data support or refute your research predictions with null and alternative hypotheses .

Hypothesis testing starts with the assumption of no difference between groups or no relationship between variables in the population—this is the null hypothesis . It’s always paired with an alternative hypothesis , which is your research prediction of an actual difference between groups or a true relationship between variables .

In this case:

• The null hypothesis (H 0 ) is that the new drug has no effect on symptoms of the disease.
• The alternative hypothesis (H 1 ) is that the drug is effective for alleviating symptoms of the disease.

Then , you decide whether the null hypothesis can be rejected based on your data and the results of a statistical test . Since these decisions are based on probabilities, there is always a risk of making the wrong conclusion.

• If your results show statistical significance , that means they are very unlikely to occur if the null hypothesis is true. In this case, you would reject your null hypothesis. But sometimes, this may actually be a Type I error.
• If your findings do not show statistical significance, they have a high chance of occurring if the null hypothesis is true. Therefore, you fail to reject your null hypothesis. But sometimes, this may be a Type II error.

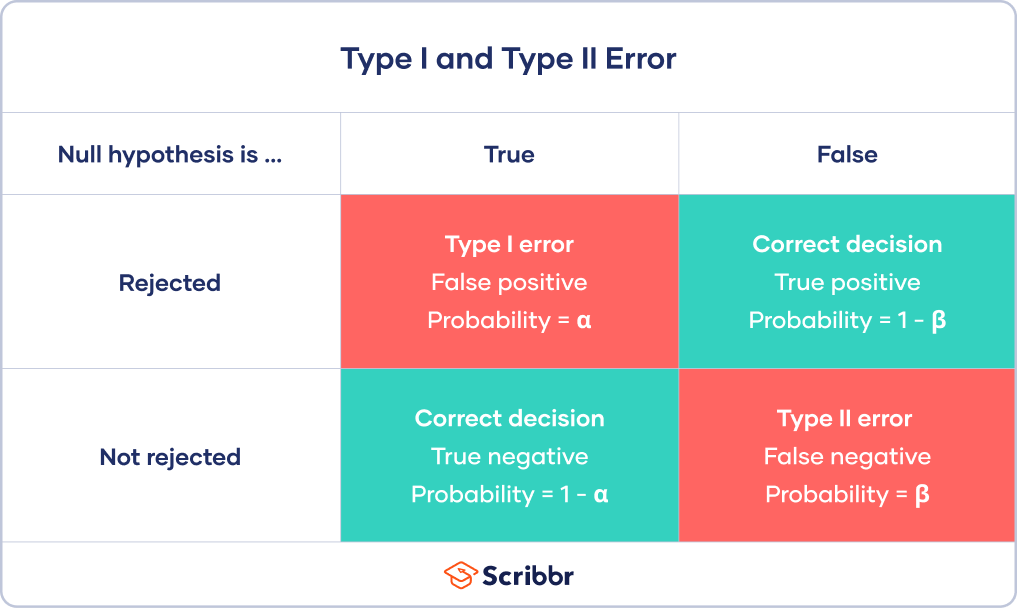
A Type I error means rejecting the null hypothesis when it’s actually true. It means concluding that results are statistically significant when, in reality, they came about purely by chance or because of unrelated factors.

The risk of committing this error is the significance level (alpha or α) you choose. That’s a value that you set at the beginning of your study to assess the statistical probability of obtaining your results ( p value).

The significance level is usually set at 0.05 or 5%. This means that your results only have a 5% chance of occurring, or less, if the null hypothesis is actually true.

If the p value of your test is lower than the significance level, it means your results are statistically significant and consistent with the alternative hypothesis. If your p value is higher than the significance level, then your results are considered statistically non-significant.

To reduce the Type I error probability, you can simply set a lower significance level.

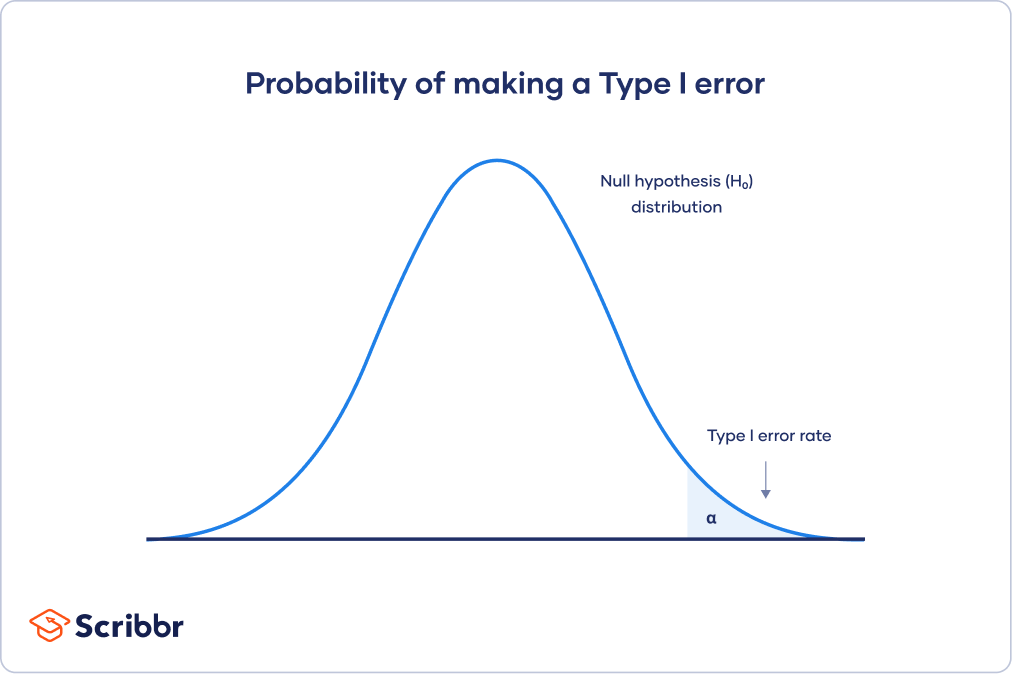
Type I error rate

The null hypothesis distribution curve below shows the probabilities of obtaining all possible results if the study were repeated with new samples and the null hypothesis were true in the population .

At the tail end, the shaded area represents alpha. It’s also called a critical region in statistics.

If your results fall in the critical region of this curve, they are considered statistically significant and the null hypothesis is rejected. However, this is a false positive conclusion, because the null hypothesis is actually true in this case!

A Type II error means not rejecting the null hypothesis when it’s actually false. This is not quite the same as “accepting” the null hypothesis, because hypothesis testing can only tell you whether to reject the null hypothesis.

Instead, a Type II error means failing to conclude there was an effect when there actually was. In reality, your study may not have had enough statistical power to detect an effect of a certain size.

Power is the extent to which a test can correctly detect a real effect when there is one. A power level of 80% or higher is usually considered acceptable.

The risk of a Type II error is inversely related to the statistical power of a study. The higher the statistical power, the lower the probability of making a Type II error.

Statistical power is determined by:

• Size of the effect : Larger effects are more easily detected.
• Measurement error : Systematic and random errors in recorded data reduce power.
• Sample size : Larger samples reduce sampling error and increase power.
• Significance level : Increasing the significance level increases power.

To (indirectly) reduce the risk of a Type II error, you can increase the sample size or the significance level.

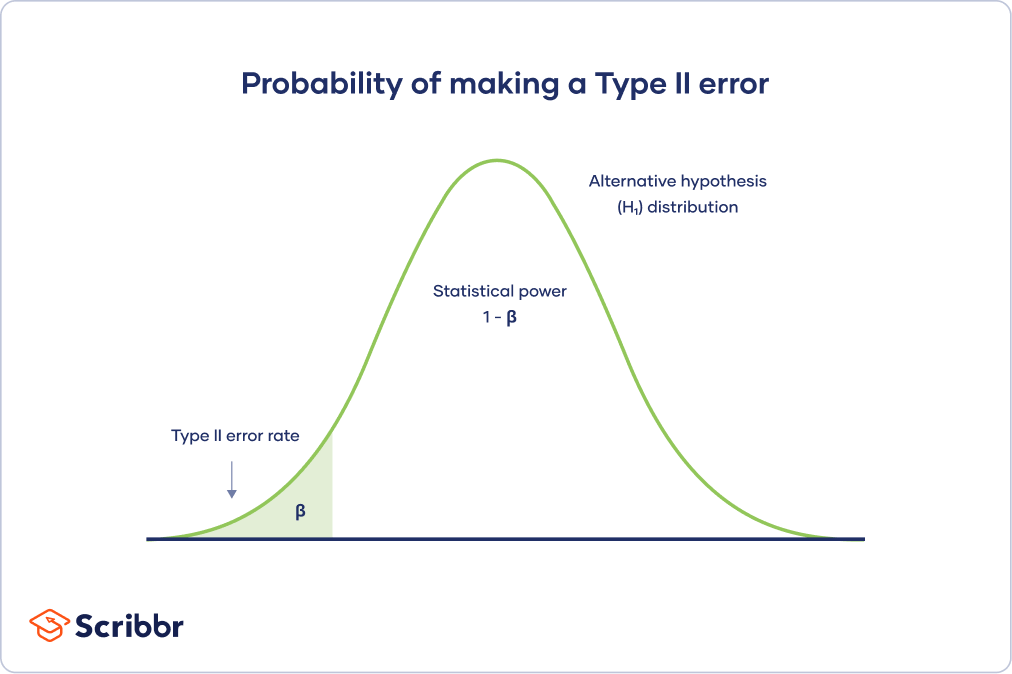
Type II error rate

The alternative hypothesis distribution curve below shows the probabilities of obtaining all possible results if the study were repeated with new samples and the alternative hypothesis were true in the population .

The Type II error rate is beta (β), represented by the shaded area on the left side. The remaining area under the curve represents statistical power, which is 1 – β.

Increasing the statistical power of your test directly decreases the risk of making a Type II error.

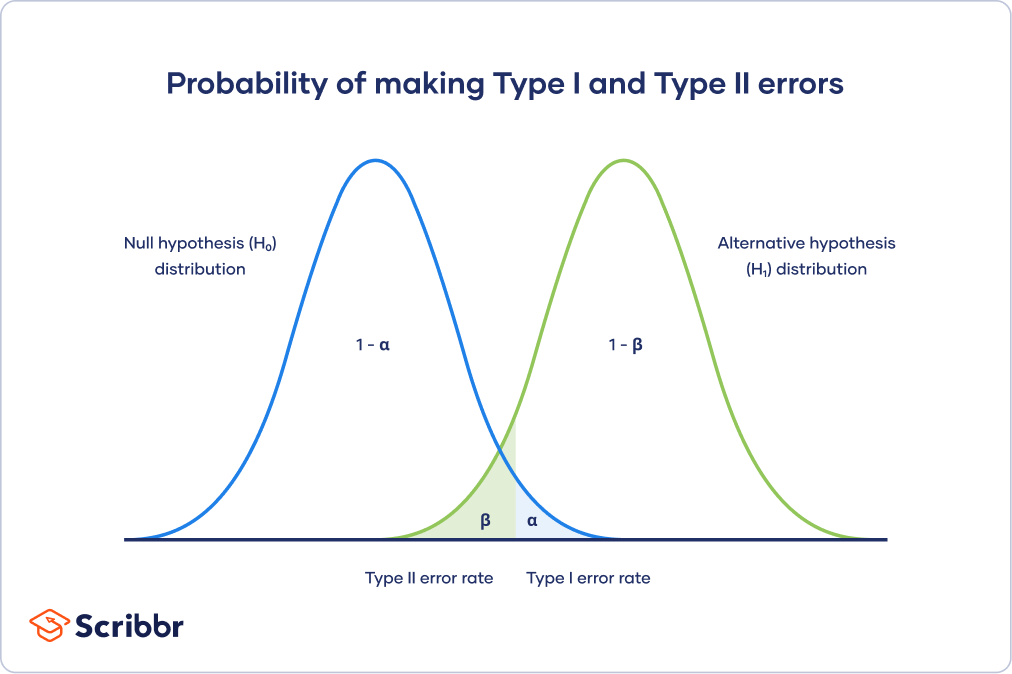
The Type I and Type II error rates influence each other. That’s because the significance level (the Type I error rate) affects statistical power, which is inversely related to the Type II error rate.

This means there’s an important tradeoff between Type I and Type II errors:

• Setting a lower significance level decreases a Type I error risk, but increases a Type II error risk.
• Increasing the power of a test decreases a Type II error risk, but increases a Type I error risk.

This trade-off is visualized in the graph below. It shows two curves:

• The null hypothesis distribution shows all possible results you’d obtain if the null hypothesis is true. The correct conclusion for any point on this distribution means not rejecting the null hypothesis.
• The alternative hypothesis distribution shows all possible results you’d obtain if the alternative hypothesis is true. The correct conclusion for any point on this distribution means rejecting the null hypothesis.

Type I and Type II errors occur where these two distributions overlap. The blue shaded area represents alpha, the Type I error rate, and the green shaded area represents beta, the Type II error rate.

By setting the Type I error rate, you indirectly influence the size of the Type II error rate as well.

It’s important to strike a balance between the risks of making Type I and Type II errors. Reducing the alpha always comes at the cost of increasing beta, and vice versa .

For statisticians, a Type I error is usually worse. In practical terms, however, either type of error could be worse depending on your research context.

A Type I error means mistakenly going against the main statistical assumption of a null hypothesis. This may lead to new policies, practices or treatments that are inadequate or a waste of resources.

In contrast, a Type II error means failing to reject a null hypothesis. It may only result in missed opportunities to innovate, but these can also have important practical consequences.

In statistics, a Type I error means rejecting the null hypothesis when it’s actually true, while a Type II error means failing to reject the null hypothesis when it’s actually false.

The risk of making a Type I error is the significance level (or alpha) that you choose. That’s a value that you set at the beginning of your study to assess the statistical probability of obtaining your results ( p value ).

To reduce the Type I error probability, you can set a lower significance level.

The risk of making a Type II error is inversely related to the statistical power of a test. Power is the extent to which a test can correctly detect a real effect when there is one.

To (indirectly) reduce the risk of a Type II error, you can increase the sample size or the significance level to increase statistical power.

Statistical significance is a term used by researchers to state that it is unlikely their observations could have occurred under the null hypothesis of a statistical test . Significance is usually denoted by a p -value , or probability value.

Statistical significance is arbitrary – it depends on the threshold, or alpha value, chosen by the researcher. The most common threshold is p < 0.05, which means that the data is likely to occur less than 5% of the time under the null hypothesis .

When the p -value falls below the chosen alpha value, then we say the result of the test is statistically significant.

In statistics, power refers to the likelihood of a hypothesis test detecting a true effect if there is one. A statistically powerful test is more likely to reject a false negative (a Type II error).

If you don’t ensure enough power in your study, you may not be able to detect a statistically significant result even when it has practical significance. Your study might not have the ability to answer your research question.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Bhandari, P. (2023, February 02). Type I & Type II Errors | Differences, Examples, Visualizations. Scribbr. Retrieved 4 November 2024, from https://www.scribbr.co.uk/stats/type-i-and-type-ii-error/

Is this article helpful?

Pritha Bhandari

• Science, Tech, Math ›
• Statistics ›
• Inferential Statistics ›

The Difference Between Type I and Type II Errors in Hypothesis Testing

• Inferential Statistics
• Statistics Tutorials
• Probability & Games
• Descriptive Statistics
• Applications Of Statistics
• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade
• Ph.D., Mathematics, Purdue University
• M.S., Mathematics, Purdue University
• B.A., Mathematics, Physics, and Chemistry, Anderson University

The statistical practice of hypothesis testing is widespread not only in statistics but also throughout the natural and social sciences. When we conduct a hypothesis test there a couple of things that could go wrong. There are two kinds of errors, which by design cannot be avoided, and we must be aware that these errors exist. The errors are given the quite pedestrian names of type I and type II errors. What are type I and type II errors, and how we distinguish between them? Briefly:

• Type I errors happen when we reject a true null hypothesis
• Type II errors happen when we fail to reject a false null hypothesis

We will explore more background behind these types of errors with the goal of understanding these statements.

Hypothesis Testing

The process of hypothesis testing can seem to be quite varied with a multitude of test statistics. But the general process is the same. Hypothesis testing involves the statement of a null hypothesis and the selection of a level of significance . The null hypothesis is either true or false and represents the default claim for a treatment or procedure. For example, when examining the effectiveness of a drug, the null hypothesis would be that the drug has no effect on a disease.

After formulating the null hypothesis and choosing a level of significance, we acquire data through observation. Statistical calculations tell us whether or not we should reject the null hypothesis.

In an ideal world, we would always reject the null hypothesis when it is false, and we would not reject the null hypothesis when it is indeed true. But there are two other scenarios that are possible, each of which will result in an error.

Type I Error

The first kind of error that is possible involves the rejection of a null hypothesis that is actually true. This kind of error is called a type I error and is sometimes called an error of the first kind.

Type I errors are equivalent to false positives. Let’s go back to the example of a drug being used to treat a disease. If we reject the null hypothesis in this situation, then our claim is that the drug does, in fact, have some effect on a disease. But if the null hypothesis is true, then, in reality, the drug does not combat the disease at all. The drug is falsely claimed to have a positive effect on a disease.

Type I errors can be controlled. The value of alpha, which is related to the level of significance that we selected has a direct bearing on type I errors. Alpha is the maximum probability that we have a type I error. For a 95% confidence level, the value of alpha is 0.05. This means that there is a 5% probability that we will reject a true null hypothesis. In the long run, one out of every twenty hypothesis tests that we perform at this level will result in a type I error.

Type II Error

The other kind of error that is possible occurs when we do not reject a null hypothesis that is false. This sort of error is called a type II error and is also referred to as an error of the second kind.

Type II errors are equivalent to false negatives. If we think back again to the scenario in which we are testing a drug, what would a type II error look like? A type II error would occur if we accepted that the drug had no effect on a disease, but in reality, it did.

The probability of a type II error is given by the Greek letter beta. This number is related to the power or sensitivity of the hypothesis test, denoted by 1 – beta.

How to Avoid Errors

Type I and type II errors are part of the process of hypothesis testing. Although the errors cannot be completely eliminated, we can minimize one type of error.

Typically when we try to decrease the probability one type of error, the probability for the other type increases. We could decrease the value of alpha from 0.05 to 0.01, corresponding to a 99% level of confidence . However, if everything else remains the same, then the probability of a type II error will nearly always increase.

Many times the real world application of our hypothesis test will determine if we are more accepting of type I or type II errors. This will then be used when we design our statistical experiment.

• Type I and Type II Errors in Statistics
• What Is the Difference Between Alpha and P-Values?
• What Level of Alpha Determines Statistical Significance?
• The Runs Test for Random Sequences
• What 'Fail to Reject' Means in a Hypothesis Test
• How to Construct a Confidence Interval for a Population Proportion
• How to Find Critical Values with a Chi-Square Table
• Null Hypothesis and Alternative Hypothesis
• An Example of a Hypothesis Test
• What Is ANOVA?
• Degrees of Freedom for Independence of Variables in Two-Way Table
• How to Find Degrees of Freedom in Statistics
• Confidence Interval for the Difference of Two Population Proportions
• An Example of Chi-Square Test for a Multinomial Experiment
• Example of a Permutation Test
• How to Calculate the Margin of Error

• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas

Type I and Type II Errors

Type I and Type II Errors are central for hypothesis testing in general, which subsequently impacts various aspects of science including but not limited to statistical analysis. False discovery refers to a Type I error where a true Null Hypothesis is incorrectly rejected. On the other end of the spectrum, Type II errors occur when a true null hypothesis fails to get rejected.

In this article, we will discuss Type I and Type II Errors in detail, including examples and differences.

Table of Content

Type I and Type II Error in Statistics

What is error, what is type i error (false positive), what is type ii error (false negative), type i and type ii errors - table, type i and type ii errors examples, examples of type i error, examples of type ii error, factors affecting type i and type ii errors, how to minimize type i and type ii errors, difference between type i and type ii errors.

In statistics , Type I and Type II errors represent two kinds of errors that can occur when making a decision about a hypothesis based on sample data. Understanding these errors is crucial for interpreting the results of hypothesis tests.

In the statistics and hypothesis testing , an error refers to the emergence of discrepancies between the result value based on observation or calculation and the actual value or expected value.

The failures may happen in different factors, such as turbulent sampling, unclear implementation, or faulty assumptions. Errors can be of many types, such as

• Measurement Error
• Calculation Error
• Human Error
• Systematic Error
• Random Error

In hypothesis testing, it is often clear which kind of error is the problem, either a Type I error or a Type II one.

Type I error, also known as a false positive , occurs in statistical hypothesis testing when a null hypothesis that is actually true is rejected. In other words, it's the error of incorrectly concluding that there is a significant effect or difference when there isn't one in reality.

In hypothesis testing, there are two competing hypotheses:

• Null Hypothesis (H 0 ): This hypothesis represents a default assumption that there is no effect, no difference, or no relationship in the population being studied.
• Alternative Hypothesis (H 1 ): This hypothesis represents the opposite of the null hypothesis. It suggests that there is a significant effect, difference, or relationship in the population.

A Type I error occurs when the null hypothesis is rejected based on the sample data, even though it is actually true in the population.

Type II error, also known as a false negative , occurs in statistical hypothesis testing when a null hypothesis that is actually false is not rejected. In other words, it's the error of failing to detect a significant effect or difference when one exists in reality.

A Type II error occurs when the null hypothesis is not rejected based on the sample data, even though it is actually false in the population. In other words, it's a failure to recognize a real effect or difference.

Suppose a medical researcher is testing a new drug to see if it's effective in treating a certain condition. The null hypothesis (H 0 ) states that the drug has no effect, while the alternative hypothesis (H 1 ) suggests that the drug is effective. If the researcher conducts a statistical test and fails to reject the null hypothesis (H 0 ), concluding that the drug is not effective, when in fact it does have an effect, this would be a Type II error.

The table given below shows the relationship between True and False:

Some of examples of type I error include:

• Medical Testing : Suppose a medical test is designed to diagnose a particular disease. The null hypothesis ( H 0 ) is that the person does not have the disease, and the alternative hypothesis ( H 1 ) is that the person does have the disease. A Type I error occurs if the test incorrectly indicates that a person has the disease (rejects the null hypothesis) when they do not actually have it.
• Legal System : In a criminal trial, the null hypothesis ( H 0 ) is that the defendant is innocent, while the alternative hypothesis ( H 1 ) is that the defendant is guilty. A Type I error occurs if the jury convicts the defendant (rejects the null hypothesis) when they are actually innocent.
• Quality Control : In manufacturing, quality control inspectors may test products to ensure they meet certain specifications. The null hypothesis ( H 0 ) is that the product meets the required standard, while the alternative hypothesis ( H 1 ) is that the product does not meet the standard. A Type I error occurs if a product is rejected (null hypothesis is rejected) as defective when it actually meets the required standard.

Using the same H 0 and H 1 , some examples of type II error include:

• Medical Testing : In a medical test designed to diagnose a disease, a Type II error occurs if the test incorrectly indicates that a person does not have the disease (fails to reject the null hypothesis) when they actually do have it.
• Legal System : In a criminal trial, a Type II error occurs if the jury acquits the defendant (fails to reject the null hypothesis) when they are actually guilty.
• Quality Control : In manufacturing, a Type II error occurs if a defective product is accepted (fails to reject the null hypothesis) as meeting the required standard.

Some of the common factors affecting errors are:

• Sample Size: In statistical hypothesis testing, larger sample sizes generally reduce the probability of both Type I and Type II errors. With larger samples, the estimates tend to be more precise, resulting in more accurate conclusions.
• Significance Level: The significance level (α) in hypothesis testing determines the probability of committing a Type I error. Choosing a lower significance level reduces the risk of Type I error but increases the risk of Type II error, and vice versa.
• Effect Size: The magnitude of the effect or difference being tested influences the probability of Type II error. Smaller effect sizes are more challenging to detect, increasing the likelihood of failing to reject the null hypothesis when it's false.
• Statistical Power: The power of Statistics (1 – β) dictates that the opportunity for rejecting a wrong null hypothesis is based on the inverse of the chance of committing a Type II error. The power level of the test rises, thus a chance of the Type II error dropping.

To minimize Type I and Type II errors in hypothesis testing, there are several strategies that can be employed based on the information from the sources provided:

• By setting a lower significance level, the chances of incorrectly rejecting the null hypothesis decrease, thus minimizing Type I errors.
• Increasing the sample size reduces the variability of the statistic, making it less likely to fall in the non-rejection region when it should be rejected, thus minimizing Type II errors.

Some of the key differences between Type I and Type II Errors are listed in the following table:

Conclusion - Type I and Type II Errors

In conclusion, type I errors occur when we mistakenly reject a true null hypothesis, while Type II errors happen when we fail to reject a false null hypothesis. Being aware of these errors helps us make more informed decisions, minimizing the risks of false conclusions.

People Also Read:

Difference between Null and Alternate Hypothesis Z-Score Table

Type I and Type II Errors - FAQs

What is type i error.

Type I Error occurs when a null hypothesis is incorrectly rejected, indicating a false positive result, concluding that there is an effect or difference when there isn't one.

What is an Example of a Type 1 Error?

An example of Type I Error is that convicting an innocent person (null hypothesis: innocence) based on insufficient evidence, incorrectly rejecting the null hypothesis of innocence.

What is Type II Error?

Type II Error happens when a null hypothesis is incorrectly accepted, failing to detect a true effect or difference when one actually exists.

What is an Example of a Type 2 Error?

An example of type 2 error is that failing to diagnose a disease in a patient (null hypothesis: absence of disease) despite them actually having the disease, incorrectly failing to reject the null hypothesis.

What is the difference between Type 1 and Type 2 Errors?

Type I error involves incorrectly rejecting a true null hypothesis, while Type II error involves failing to reject a false null hypothesis. In simpler terms, Type I error is a false positive, while Type II error is a false negative.

What is Type 3 Error?

Type 3 Error is not a standard statistical term. It's sometimes informally used to describe situations where the researcher correctly rejects the null hypothesis but for the wrong reason, often due to a flaw in the experimental design or analysis.

How are Type I and Type II Errors related to hypothesis testing?

In hypothesis testing, Type I Error relates to the significance level (α), which represents the probability of rejecting a true null hypothesis. Type II Error relates to the power of the test (β), which represents the probability of failing to reject a false null hypothesis.

What are some examples of Type I and Type II Errors?

Type I Error: Rejecting a null hypothesis that a new drug has no side effects when it actually does (false positive). Type II Error: Failing to reject a null hypothesis that a new drug has no effect when it actually does (false negative).

How can one minimize Type I and Type II Errors?

Type I Error can be minimized by choosing a lower significance level (α) for hypothesis testing. Type II Error can be minimized by increasing the sample size or improving the sensitivity of the test.

What is the relationship between Type I and Type II Errors?

There is often a trade-off between Type I and Type II Errors. Decreasing the probability of one type of error typically increases the probability of the other.

How do Type I and Type II Errors impact decision-making?

Type I Errors can lead to false conclusions, such as mistakenly believing a treatment is effective when it's not. Type II Errors can result in missed opportunities, such as failing to identify an effective treatment.

In which fields are Type I and Type II Errors commonly encountered?

Type I and Type II Errors are encountered in various fields, including medical research, quality control, criminal justice, and market research.

Similar Reads

Please login to comment..., improve your coding skills with practice.

What kind of Experience do you want to share?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6: The Foundations of Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 50015

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

• 6.1: Developing Hypotheses
• 6.2: One-Tailed vs. Two-Tailed Tests
• 6.3: Sampling Distributions
• 6.4: Hypothesis Testing
• 6.5: Errors and Statistical Significance
• 6.6: Choosing Statistical Tests
• 6.7: References