problem solving involving average speed

Average Speed Problems

Related Pages Rate, Time, Distance Solving Speed, Time, Distance Problems Using Algebra More Algebra Lessons

In these lessons, we will learn how to solve word problems involving average speed.

There are three main types of average problems commonly encountered in school algebra: Average (Arithmetic Mean) Weighted Average and Average Speed.

How to calculate Average Speed?

The following diagram shows the formula for average speed. Scroll down the page for more examples and solutions on calculating the average speed.

Examples Of Average Speed Problems

Example: John drove for 3 hours at a rate of 50 miles per hour and for 2 hours at 60 miles per hour. What was his average speed for the whole journey?

Solution: Step 1: The formula for distance is

Distance = Rate × Time Total distance = 50 × 3 + 60 × 2 = 270

Step 2: Total time = 3 + 2 = 5

Step 3: Using the formula:

Answer: The average speed is 54 miles per hour.

Be careful! You will get the wrong answer if you add the two speeds and divide the answer by two.

How To Solve The Average Speed Problem?

How to calculate the average speed?

Example: The speed paradox: If I drive from Oxford to Cambridge at 40 miles per hour and then from Cambridge to Oxford at 60 miles per hour, what is my average speed for the whole journey?

How To Find The Average Speed For A Round Trip?

Example: On Alberto’s drive to his aunt’s house, the traffic was light, and he drove the 45-mile trip in one hour. However, the return trip took his two hours. What was his average trip for the round trip?

How To Find The Average Speed Of An Airplane With Good And Bad Weather?

Example: Mae took a non-stop flight to visit her grandmother. The 750-mile trip took three hours and 45 minutes. Because of the bad weather, the return trip took four hours and 45 minutes. What was her average speed for the round trip?

How To Relate Speed To Distance And Time?

If you are traveling in a car that travels 80km along a road in one hour, we say that you are traveling at an average of 80kn/h.

Average speed is the total distance divided by the total time for the trip. Therefore, speed is distance divided by time.

Instantaneous speed is the speed at which an object is traveling at any particular instant.

If the instantaneous speed of a car remains the same over a period of time, then we say that the car is traveling with constant speed.

The average speed of an object is the same as its instantaneous speed if that object is traveling at a constant speed.

How To Calculate Average Speed In Word Problems?

Example: Keri rollerblades to school, a total distance of 4.5km. She has to slow down twice to cross busy streets, but overall the journey takes her 0.65h. What is Keri’s average speed during the trip?

How To Use Average Speed To Calculate The Distance Traveled?

Example: Elle drives 169 miles from Sheffield to London. Her average speed is 65 mph. She leaves Sheffield at 6:30 a.m. Does she arrive in London by 9:00 a.m.?

How To Use Average Speed To Calculate The Time Taken?

Example: Marie Ann is trying to predict the time required to ride her bike to the nearby beach. She knows that the distance is 45 km and, from other trips, that she can usually average about 20 km/h. Predict how long the trip will take.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Number Charts
Multiplication
Long division
Basic operations
Telling time
Place value
Roman numerals
Fractions & related
Add, subtract, multiply, and divide fractions
Mixed numbers vs. fractions
Equivalent fractions
Prime factorization & factors
Fraction Calculator
Decimals & Percent
Add, subtract, multiply, and divide decimals
Fractions to decimals
Percents to decimals
Percentage of a number
Percent word problems
Classify triangles
Classify quadrilaterals
Circle worksheets
Area & perimeter of rectangles
Area of triangles & polygons
Coordinate grid, including moves & reflections
Volume & surface area
Pre-algebra
Square Roots
Order of operations
Scientific notation
Proportions
Ratio word problems
Write expressions
Evaluate expressions
Simplify expressions
Linear equations
Linear inequalities
Graphing & slope
Equation calculator
Equation editor
Elementary Math Games
Addition and subtraction
Math facts practice
The four operations
Factoring and number theory
Geometry topics
Middle/High School
Statistics & Graphs
Probability
Trigonometry
Logic and proof
For all levels
Favorite math puzzles
Favorite challenging puzzles
Math in real world
Problem solving & projects
For gifted children
Math history
Math games and fun websites
Interactive math tutorials
Math help & online tutoring
Assessment, review & test prep
Online math curricula

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 8: Rational Expressions

8.8 Rate Word Problems: Speed, Distance and Time

Distance, rate and time problems are a standard application of linear equations. When solving these problems, use the relationship rate (speed or velocity) times time equals distance .

[latex]r\cdot t=d[/latex]

For example, suppose a person were to travel 30 km/h for 4 h. To find the total distance, multiply rate times time or (30km/h)(4h) = 120 km.

The problems to be solved here will have a few more steps than described above. So to keep the information in the problem organized, use a table. An example of the basic structure of the table is below:

The third column, distance, will always be filled in by multiplying the rate and time columns together. If given a total distance of both persons or trips, put this information in the distance column. Now use this table to set up and solve the following examples.

Example 8.8.1

Joey and Natasha start from the same point and walk in opposite directions. Joey walks 2 km/h faster than Natasha. After 3 hours, they are 30 kilometres apart. How fast did each walk?

The distance travelled by both is 30 km. Therefore, the equation to be solved is:

[latex]\begin{array}{rrrrrrl} 3r&+&3(r&+&2)&=&30 \\ 3r&+&3r&+&6&=&30 \\ &&&-&6&&-6 \\ \hline &&&&\dfrac{6r}{6}&=&\dfrac{24}{6} \\ \\ &&&&r&=&4 \text{ km/h} \end{array}[/latex]

This means that Natasha walks at 4 km/h and Joey walks at 6 km/h.

Example 8.8.2

Nick and Chloe left their campsite by canoe and paddled downstream at an average speed of 12 km/h. They turned around and paddled back upstream at an average rate of 4 km/h. The total trip took 1 hour. After how much time did the campers turn around downstream?

The distance travelled downstream is the same distance that they travelled upstream. Therefore, the equation to be solved is:

[latex]\begin{array}{rrlll} 12(t)&=&4(1&-&t) \\ 12t&=&4&-&4t \\ +4t&&&+&4t \\ \hline \dfrac{16t}{16}&=&\dfrac{4}{16}&& \\ \\ t&=&0.25&& \end{array}[/latex]

This means the campers paddled downstream for 0.25 h and spent 0.75 h paddling back.

Example 8.8.3

Terry leaves his house riding a bike at 20 km/h. Sally leaves 6 h later on a scooter to catch up with him travelling at 80 km/h. How long will it take her to catch up with him?

The distance travelled by both is the same. Therefore, the equation to be solved is:

[latex]\begin{array}{rrrrr} 20(t)&=&80(t&-&6) \\ 20t&=&80t&-&480 \\ -80t&&-80t&& \\ \hline \dfrac{-60t}{-60}&=&\dfrac{-480}{-60}&& \\ \\ t&=&8&& \end{array}[/latex]

This means that Terry travels for 8 h and Sally only needs 2 h to catch up to him.

Example 8.8.4

On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took 2.5 h. For how long did the car travel 40 km/h?

[latex]\begin{array}{rrrrrrr} 55(t)&+&40(2.5&-&t)&=&130 \\ 55t&+&100&-&40t&=&130 \\ &-&100&&&&-100 \\ \hline &&&&\dfrac{15t}{15}&=&\dfrac{30}{15} \\ \\ &&&&t&=&2 \end{array}[/latex]

This means that the time spent travelling at 40 km/h was 0.5 h.

Distance, time and rate problems have a few variations that mix the unknowns between distance, rate and time. They generally involve solving a problem that uses the combined distance travelled to equal some distance or a problem in which the distances travelled by both parties is the same. These distance, rate and time problems will be revisited later on in this textbook where quadratic solutions are required to solve them.

For Questions 1 to 8, find the equations needed to solve the problems. Do not solve.

A is 60 kilometres from B. An automobile at A starts for B at the rate of 20 km/h at the same time that an automobile at B starts for A at the rate of 25 km/h. How long will it be before the automobiles meet?
Two automobiles are 276 kilometres apart and start to travel toward each other at the same time. They travel at rates differing by 5 km/h. If they meet after 6 h, find the rate of each.
Two trains starting at the same station head in opposite directions. They travel at the rates of 25 and 40 km/h, respectively. If they start at the same time, how soon will they be 195 kilometres apart?
Two bike messengers, Jerry and Susan, ride in opposite directions. If Jerry rides at the rate of 20 km/h, at what rate must Susan ride if they are 150 kilometres apart in 5 hours?
A passenger and a freight train start toward each other at the same time from two points 300 kilometres apart. If the rate of the passenger train exceeds the rate of the freight train by 15 km/h, and they meet after 4 hours, what must the rate of each be?
Two automobiles started travelling in opposite directions at the same time from the same point. Their rates were 25 and 35 km/h, respectively. After how many hours were they 180 kilometres apart?
A man having ten hours at his disposal made an excursion by bike, riding out at the rate of 10 km/h and returning on foot at the rate of 3 km/h. Find the distance he rode.
A man walks at the rate of 4 km/h. How far can he walk into the country and ride back on a trolley that travels at the rate of 20 km/h, if he must be back home 3 hours from the time he started?

Solve Questions 9 to 22.

A boy rides away from home in an automobile at the rate of 28 km/h and walks back at the rate of 4 km/h. The round trip requires 2 hours. How far does he ride?
A motorboat leaves a harbour and travels at an average speed of 15 km/h toward an island. The average speed on the return trip was 10 km/h. How far was the island from the harbour if the trip took a total of 5 hours?
A family drove to a resort at an average speed of 30 km/h and later returned over the same road at an average speed of 50 km/h. Find the distance to the resort if the total driving time was 8 hours.
As part of his flight training, a student pilot was required to fly to an airport and then return. The average speed to the airport was 90 km/h, and the average speed returning was 120 km/h. Find the distance between the two airports if the total flying time was 7 hours.
Sam starts travelling at 4 km/h from a campsite 2 hours ahead of Sue, who travels 6 km/h in the same direction. How many hours will it take for Sue to catch up to Sam?
A man travels 5 km/h. After travelling for 6 hours, another man starts at the same place as the first man did, following at the rate of 8 km/h. When will the second man overtake the first?
A motorboat leaves a harbour and travels at an average speed of 8 km/h toward a small island. Two hours later, a cabin cruiser leaves the same harbour and travels at an average speed of 16 km/h toward the same island. How many hours after the cabin cruiser leaves will it be alongside the motorboat?
A long distance runner started on a course, running at an average speed of 6 km/h. One hour later, a second runner began the same course at an average speed of 8 km/h. How long after the second runner started will they overtake the first runner?
Two men are travelling in opposite directions at the rate of 20 and 30 km/h at the same time and from the same place. In how many hours will they be 300 kilometres apart?
Two trains start at the same time from the same place and travel in opposite directions. If the rate of one is 6 km/h more than the rate of the other and they are 168 kilometres apart at the end of 4 hours, what is the rate of each?
Two cyclists start from the same point and ride in opposite directions. One cyclist rides twice as fast as the other. In three hours, they are 72 kilometres apart. Find the rate of each cyclist.
Two small planes start from the same point and fly in opposite directions. The first plane is flying 25 km/h slower than the second plane. In two hours, the planes are 430 kilometres apart. Find the rate of each plane.
On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took a total of 2.5 hours. For how long did the car travel at 40 km/h?
Running at an average rate of 8 m/s, a sprinter ran to the end of a track and then jogged back to the starting point at an average of 3 m/s. The sprinter took 55 s to run to the end of the track and jog back. Find the length of the track.

Answer Key 8.8

Share This Book

AVERAGE SPEED PROBLEMS

Problem 1 :

A person travels from New York to Washington at the rate of 45 miles per hour and comes backs to the New York at the rate of 55 miles per hour. What is his average speed for the whole journey?

Here, both the ways, he covers the same distance.

Then, the formula to find average speed is

= 2xy/(x + y)

x ----> Rate at which he travels from New York to Washington

y ----> Rate at which he travels from New York to Washington

So, the average speed is

= (2 ⋅ 45 ⋅ 55)/(45 + 55)

So, the average speed for the whole journey is 45 miles per hour.

Problem 2 :

A man takes 10 hours to go to a place and come back by walking both the ways. He could have gained 2 hours by riding both the ways. The distance covered in the whole journey is 18 miles. Find the average speed for the whole journey if he goes by walking and comes back by riding.

Given : A man takes 10 hours to go to a place and come back by walking both the ways.

walking + walking = 10 hours

2 ⋅ w alking = 10 hours

walking = 5 hours

Given : He could have gained 2 hours by riding both the ways.

riding + riding = 8 hours

2 ⋅ riding = 8 hours

riding = 4 hours

If he goes by walking and comes back by riding, time taken by him :

walking + riding = 5 + 4

walking + riding = 9 hours

total time taken = 9 hours

total distance covered = 18 miles

= total distance/total time

So, the required average speed is 2 miles per hour.

Problem 3 :

Lily takes 3 hours to travel from place A to place B at the rate of 60 miles per hour. She takes 2 hours to travel from place B to C with 50% increased speed. Find the average speed from place A to C.

speed (from A to B) = 60 miles/hour

speed (from B to C) = 90 miles/hour (50% increased)

Formula to find distance is

= rate ⋅ time

Distance from A to B is

= 60 ⋅ 3

= 180 miles

Distance from B to C :

= 90 ⋅ 2

Total distance traveled from A to B is

= 180 + 180

= 360 miles

Total time taken from A to B is

Formula to find average speed is

So, the average speed from place A to B is 72 miles/hour.

Problem 4 :

Distance from A to B = 200 miles

Distance from B to C = 300 miles

Distance from C to D = 540 miles

The speed from B to C is 50% more than A to B. The speed from C to D is 50% more than B to C. If the speed from A to B is 40 miles per hour, find the average speed from A to D.

speed (from A to B) = 40 miles/hour

speed (from B to C) = 60 miles/hour (50% more)

speed (from C to D) = 90 miles/hour (50% more)

Formula to find time is

= distance/time

time (A to B) = 200/40 = 5 hours

time (B to C) = 300/60 = 5 hours

time (C to D) = 540/90 = 6 hours

Total time taken from A to D is

= 5 + 5 + 6

Total distance from A to D is

= 200 + 300 + 540

= 1040 miles

So, the average speed from A to D is 65 miles per hour.

Problem 5 :

Time (A to B) = 3 hours

Time (B to C) = 5 hours

Time (C to D) = 6 hours

If the distances from A to B, B to C and C to D are equal and the speed from A to B is 70 miles per hour, find the average speed from A to D

= 70 ⋅ 3

= 210 miles

Given : Distance from A to B, B to C and C to D are equal.

= 210 + 210 + 210

= 630 miles

Total time taken A to D is

= 3 + 5 + 6

So, the average speed from A to D is 45 miles per hour.

Kindly mail your feedback to [email protected]

We always appreciate your feedback.

Sat Math Practice
SAT Math Worksheets
PEMDAS Rule
BODMAS rule
GEMDAS Order of Operations
Math Calculators
Transformations of Functions
Order of rotational symmetry
Lines of symmetry
Compound Angles
Quantitative Aptitude Tricks
Trigonometric ratio table
Word Problems
Times Table Shortcuts
10th CBSE solution
PSAT Math Preparation
Privacy Policy
Laws of Exponents

Recent Articles

Worksheet on Proving Trigonometric Identities

Nov 02, 24 11:58 PM

AP Precalculus Problems and Solutions (Part - 1)

Oct 30, 24 10:07 AM

SAT Math Resources (Videos, Concepts, Worksheets and More)

Oct 29, 24 06:24 AM

Gurumuda Networks

Average speed and average velocity – problems and solutions

Solved Problems in Linear Motion – Average speed and average velocity

1. A car travels along a straight road to the east for 100 meters in 4 seconds, then go the west for 50 meters in 1 second. Determine average speed and average velocity.

Distance = 100 meters + 50 meters = 150 meters

Displacement = 100 meters – 50 meters = 50 meters, to east.

Time elapsed = 4 seconds + 1 second = 5 seconds .

Average speed = Distance / time elapsed = 150 meters / 5 seconds = 30 meters/second.

Average velocity = Displacement / time elapsed = 50 meters / 5 seconds = 10 meters/second .

2. A person walks 4 meters east in 1 second, then walks 3 meters north in 1 second. Determine average speed and average velocity.

Average speed and average velocity - problems and solutions 1

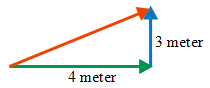
Time elapsed = 1 second + 1 second = 2 seconds.

Average speed = distance / time elapsed = 7 meters / 2 seconds = 3.5 meters/second

Average velocity = displacement / time elapsed = 5 meters / 2 seconds = 2.5 meters/second

3. A runner travels around rectangle track with length = 50 meters and width = 20 meters. After travels around rectangle track two times, runner back to starting point. If time elapsed = 100 seconds, determine average speed and average velocity.

Circumference of rectangle = 2(50 meters) + 2(20 meters) = 100 meters + 40 meters = 140 meters.

Travels around rectangle 2 times = 2(140 meters) = 280 meters.

Distance = 280 meter .

Displacement = 0 meter . ( runner back to start point)

Average speed = distance / time elapsed = 280 meters / 100 seconds = 2.8 meters/second.

Average velocity = displacement / time elapsed = 0 / 100 seconds = 0.

[wpdm_package id=’505′]

[wpdm_package id=’517′]

Distance and displacement
Average speed and average velocity
Constant velocity
Constant acceleration
Free fall motion
Down motion in free fall
Up and down motion in free fall

TPC and eLearning
What's NEW at TPC?
Read Watch Interact
Practice Review Test
Teacher-Tools
Request a Demo
Get A Quote
Subscription Selection
Seat Calculator
Ad Free Account
Edit Profile Settings
Metric Conversions Questions
Metric System Questions
Metric Estimation Questions
Significant Digits Questions
Proportional Reasoning
Acceleration
Distance-Displacement
Dots and Graphs
Graph That Motion
Match That Graph
Name That Motion
Motion Diagrams
Pos'n Time Graphs Numerical
Pos'n Time Graphs Conceptual
Up And Down - Questions
Balanced vs. Unbalanced Forces
Change of State
Force and Motion
Mass and Weight
Match That Free-Body Diagram
Net Force (and Acceleration) Ranking Tasks
Newton's Second Law
Normal Force Card Sort
Recognizing Forces
Air Resistance and Skydiving
Solve It! with Newton's Second Law
Which One Doesn't Belong?
Component Addition Questions
Head-to-Tail Vector Addition
Projectile Mathematics
Trajectory - Angle Launched Projectiles
Trajectory - Horizontally Launched Projectiles
Vector Addition
Vector Direction
Which One Doesn't Belong? Projectile Motion
Forces in 2-Dimensions
Being Impulsive About Momentum
Explosions - Law Breakers
Hit and Stick Collisions - Law Breakers
Case Studies: Impulse and Force
Impulse-Momentum Change Table
Keeping Track of Momentum - Hit and Stick
Keeping Track of Momentum - Hit and Bounce
What's Up (and Down) with KE and PE?
Energy Conservation Questions
Energy Dissipation Questions
Energy Ranking Tasks
LOL Charts (a.k.a., Energy Bar Charts)
Match That Bar Chart
Words and Charts Questions
Name That Energy
Stepping Up with PE and KE Questions
Case Studies - Circular Motion
Circular Logic
Forces and Free-Body Diagrams in Circular Motion
Gravitational Field Strength
Universal Gravitation
Angular Position and Displacement
Linear and Angular Velocity
Angular Acceleration
Rotational Inertia
Balanced vs. Unbalanced Torques
Getting a Handle on Torque
Torque-ing About Rotation
Properties of Matter
Fluid Pressure
Buoyant Force
Sinking, Floating, and Hanging
Pascal's Principle
Flow Velocity
Bernoulli's Principle
Balloon Interactions
Charge and Charging
Charge Interactions
Charging by Induction
Conductors and Insulators
Coulombs Law
Electric Field
Electric Field Intensity
Polarization
Case Studies: Electric Power
Know Your Potential
Light Bulb Anatomy
I = ∆V/R Equations as a Guide to Thinking
Parallel Circuits - ∆V = I•R Calculations
Resistance Ranking Tasks
Series Circuits - ∆V = I•R Calculations
Series vs. Parallel Circuits
Equivalent Resistance
Period and Frequency of a Pendulum
Pendulum Motion: Velocity and Force
Energy of a Pendulum
Period and Frequency of a Mass on a Spring
Horizontal Springs: Velocity and Force
Vertical Springs: Velocity and Force
Energy of a Mass on a Spring
Decibel Scale
Frequency and Period
Closed-End Air Columns
Name That Harmonic: Strings
Rocking the Boat
Wave Basics
Matching Pairs: Wave Characteristics
Wave Interference
Waves - Case Studies
Color Addition and Subtraction
Color Filters
If This, Then That: Color Subtraction
Light Intensity
Color Pigments
Converging Lenses
Curved Mirror Images
Law of Reflection
Refraction and Lenses
Total Internal Reflection
Who Can See Who?
Lab Equipment
Lab Procedures
Formulas and Atom Counting
Atomic Models
Bond Polarity
Entropy Questions
Cell Voltage Questions
Heat of Formation Questions
Reduction Potential Questions
Oxidation States Questions
Measuring the Quantity of Heat
Hess's Law
Oxidation-Reduction Questions
Galvanic Cells Questions
Thermal Stoichiometry
Molecular Polarity
Quantum Mechanics
Balancing Chemical Equations
Bronsted-Lowry Model of Acids and Bases
Classification of Matter
Collision Model of Reaction Rates
Density Ranking Tasks
Dissociation Reactions
Complete Electron Configurations
Elemental Measures
Enthalpy Change Questions
Equilibrium Concept
Equilibrium Constant Expression
Equilibrium Calculations - Questions
Equilibrium ICE Table
Intermolecular Forces Questions
Ionic Bonding
Lewis Electron Dot Structures
Limiting Reactants
Line Spectra Questions
Mass Stoichiometry
Measurement and Numbers
Metals, Nonmetals, and Metalloids
Metric Estimations
Metric System
Molarity Ranking Tasks
Mole Conversions
Name That Element
Names to Formulas
Names to Formulas 2
Nuclear Decay
Particles, Words, and Formulas
Periodic Trends
Precipitation Reactions and Net Ionic Equations
Pressure Concepts
Pressure-Temperature Gas Law
Pressure-Volume Gas Law
Chemical Reaction Types
Significant Digits and Measurement
States Of Matter Exercise
Stoichiometry Law Breakers
Stoichiometry - Math Relationships
Subatomic Particles
Spontaneity and Driving Forces
Gibbs Free Energy
Volume-Temperature Gas Law
Acid-Base Properties
Energy and Chemical Reactions
Chemical and Physical Properties
Valence Shell Electron Pair Repulsion Theory
Writing Balanced Chemical Equations
Mission CG1
Mission CG10
Mission CG2
Mission CG3
Mission CG4
Mission CG5
Mission CG6
Mission CG7
Mission CG8
Mission CG9
Mission EC1
Mission EC10
Mission EC11
Mission EC12
Mission EC2
Mission EC3
Mission EC4
Mission EC5
Mission EC6
Mission EC7
Mission EC8
Mission EC9
Mission RL1
Mission RL2
Mission RL3
Mission RL4
Mission RL5
Mission RL6
Mission KG7
Mission RL8
Mission KG9
Mission RL10
Mission RL11
Mission RM1
Mission RM2
Mission RM3
Mission RM4
Mission RM5
Mission RM6
Mission RM8
Mission RM10
Mission LC1
Mission RM11
Mission LC2
Mission LC3
Mission LC4
Mission LC5
Mission LC6
Mission LC8
Mission SM1
Mission SM2
Mission SM3
Mission SM4
Mission SM5
Mission SM6
Mission SM8
Mission SM10
Mission KG10
Mission SM11
Mission KG2
Mission KG3
Mission KG4
Mission KG5
Mission KG6
Mission KG8
Mission KG11
Mission F2D1
Mission F2D2
Mission F2D3
Mission F2D4
Mission F2D5
Mission F2D6
Mission KC1
Mission KC2
Mission KC3
Mission KC4
Mission KC5
Mission KC6
Mission KC7
Mission KC8
Mission AAA
Mission SM9
Mission LC7
Mission LC9
Mission NL1
Mission NL2
Mission NL3
Mission NL4
Mission NL5
Mission NL6
Mission NL7
Mission NL8
Mission NL9
Mission NL10
Mission NL11
Mission NL12
Mission MC1
Mission MC10
Mission MC2
Mission MC3
Mission MC4
Mission MC5
Mission MC6
Mission MC7
Mission MC8
Mission MC9
Mission RM7
Mission RM9
Mission RL7
Mission RL9
Mission SM7
Mission SE1
Mission SE10
Mission SE11
Mission SE12
Mission SE2
Mission SE3
Mission SE4
Mission SE5
Mission SE6
Mission SE7
Mission SE8
Mission SE9
Mission VP1
Mission VP10
Mission VP2
Mission VP3
Mission VP4
Mission VP5
Mission VP6
Mission VP7
Mission VP8
Mission VP9
Mission WM1
Mission WM2
Mission WM3
Mission WM4
Mission WM5
Mission WM6
Mission WM7
Mission WM8
Mission WE1
Mission WE10
Mission WE2
Mission WE3
Mission WE4
Mission WE5
Mission WE6
Mission WE7
Mission WE8
Mission WE9
Vector Walk Interactive
Name That Motion Interactive
Kinematic Graphing 1 Concept Checker
Kinematic Graphing 2 Concept Checker
Graph That Motion Interactive
Two Stage Rocket Interactive
Rocket Sled Concept Checker
Force Concept Checker
Free-Body Diagrams Concept Checker
Free-Body Diagrams The Sequel Concept Checker
Skydiving Concept Checker
Elevator Ride Concept Checker
Vector Addition Concept Checker
Vector Walk in Two Dimensions Interactive
Name That Vector Interactive
River Boat Simulator Concept Checker
Projectile Simulator 2 Concept Checker
Projectile Simulator 3 Concept Checker
Hit the Target Interactive
Turd the Target 1 Interactive
Turd the Target 2 Interactive
Balance It Interactive
Go For The Gold Interactive
Egg Drop Concept Checker
Fish Catch Concept Checker
Exploding Carts Concept Checker
Collision Carts - Inelastic Collisions Concept Checker
Its All Uphill Concept Checker
Stopping Distance Concept Checker
Chart That Motion Interactive
Roller Coaster Model Concept Checker
Uniform Circular Motion Concept Checker
Horizontal Circle Simulation Concept Checker
Vertical Circle Simulation Concept Checker
Race Track Concept Checker
Gravitational Fields Concept Checker
Orbital Motion Concept Checker
Angular Acceleration Concept Checker
Balance Beam Concept Checker
Torque Balancer Concept Checker
Aluminum Can Polarization Concept Checker
Charging Concept Checker
Name That Charge Simulation
Coulomb's Law Concept Checker
Electric Field Lines Concept Checker
Put the Charge in the Goal Concept Checker
Circuit Builder Concept Checker (Series Circuits)
Circuit Builder Concept Checker (Parallel Circuits)
Circuit Builder Concept Checker (∆V-I-R)
Circuit Builder Concept Checker (Voltage Drop)
Equivalent Resistance Interactive
Pendulum Motion Simulation Concept Checker
Mass on a Spring Simulation Concept Checker
Particle Wave Simulation Concept Checker
Boundary Behavior Simulation Concept Checker
Slinky Wave Simulator Concept Checker
Simple Wave Simulator Concept Checker
Wave Addition Simulation Concept Checker
Standing Wave Maker Simulation Concept Checker
Color Addition Concept Checker
Painting With CMY Concept Checker
Stage Lighting Concept Checker
Filtering Away Concept Checker
InterferencePatterns Concept Checker
Young's Experiment Interactive
Plane Mirror Images Interactive
Who Can See Who Concept Checker
Optics Bench (Mirrors) Concept Checker
Name That Image (Mirrors) Interactive
Refraction Concept Checker
Total Internal Reflection Concept Checker
Optics Bench (Lenses) Concept Checker
Kinematics Preview
Velocity Time Graphs Preview
Moving Cart on an Inclined Plane Preview
Stopping Distance Preview
Cart, Bricks, and Bands Preview
Fan Cart Study Preview
Friction Preview
Coffee Filter Lab Preview
Friction, Speed, and Stopping Distance Preview
Up and Down Preview
Projectile Range Preview
Ballistics Preview
Juggling Preview
Marshmallow Launcher Preview
Air Bag Safety Preview
Colliding Carts Preview
Collisions Preview
Engineering Safer Helmets Preview
Push the Plow Preview
Its All Uphill Preview
Energy on an Incline Preview
Modeling Roller Coasters Preview
Hot Wheels Stopping Distance Preview
Ball Bat Collision Preview
Energy in Fields Preview
Weightlessness Training Preview
Roller Coaster Loops Preview
Universal Gravitation Preview
Keplers Laws Preview
Kepler's Third Law Preview
Charge Interactions Preview
Sticky Tape Experiments Preview
Wire Gauge Preview
Voltage, Current, and Resistance Preview
Light Bulb Resistance Preview
Series and Parallel Circuits Preview
Thermal Equilibrium Preview
Linear Expansion Preview
Heating Curves Preview
Electricity and Magnetism - Part 1 Preview
Electricity and Magnetism - Part 2 Preview
Vibrating Mass on a Spring Preview
Period of a Pendulum Preview
Wave Speed Preview
Slinky-Experiments Preview
Standing Waves in a Rope Preview
Sound as a Pressure Wave Preview
DeciBel Scale Preview
DeciBels, Phons, and Sones Preview
Sound of Music Preview
Shedding Light on Light Bulbs Preview
Models of Light Preview
Electromagnetic Radiation Preview
Electromagnetic Spectrum Preview
EM Wave Communication Preview
Digitized Data Preview
Light Intensity Preview
Concave Mirrors Preview
Object Image Relations Preview
Snells Law Preview
Reflection vs. Transmission Preview
Magnification Lab Preview
Reactivity Preview
Ions and the Periodic Table Preview
Periodic Trends Preview
Chemical Reactions Preview
Intermolecular Forces Preview
Melting Points and Boiling Points Preview
Bond Energy and Reactions Preview
Reaction Rates Preview
Ammonia Factory Preview
Stoichiometry Preview
Nuclear Chemistry Preview
Gaining Teacher Access
Task Tracker Directions
Conceptual Physics Course
On-Level Physics Course
Honors Physics Course
Chemistry Concept Builders
All Chemistry Resources
Users Voice
Tasks and Classes
Webinars and Trainings
Subscription
Subscription Locator
1-D Kinematics
Newton's Laws
Vectors - Motion and Forces in Two Dimensions
Momentum and Its Conservation
Work and Energy
Circular Motion and Satellite Motion
Thermal Physics
Static Electricity
Electric Circuits
Vibrations and Waves
Sound Waves and Music
Light and Color
Reflection and Mirrors
Measurement and Calculations
Elements, Atoms, and Ions
Compounds,Names, and Formulas
The Modern Atomic Model
Chemical Bonding
About the Physics Interactives
Task Tracker
Usage Policy
Newtons Laws
Vectors and Projectiles
Forces in 2D
Momentum and Collisions
Circular and Satellite Motion
Balance and Rotation
Electromagnetism
Waves and Sound
Atomic Physics
Forces in Two Dimensions
Work, Energy, and Power
Circular Motion and Gravitation
Sound Waves
1-Dimensional Kinematics
Circular, Satellite, and Rotational Motion
Einstein's Theory of Special Relativity
Waves, Sound and Light
QuickTime Movies
About the Concept Builders
Pricing For Schools
Directions for Version 2
Measurement and Units
Relationships and Graphs
Rotation and Balance
Vibrational Motion
Reflection and Refraction
Teacher Accounts
Kinematic Concepts
Kinematic Graphing
Wave Motion
Sound and Music
About CalcPad
1D Kinematics
Vectors and Forces in 2D
Simple Harmonic Motion
Rotational Kinematics
Rotation and Torque
Rotational Dynamics
Electric Fields, Potential, and Capacitance
Transient RC Circuits
Light Waves
Units and Measurement
Stoichiometry
Molarity and Solutions
Thermal Chemistry
Acids and Bases
Kinetics and Equilibrium
Solution Equilibria
Oxidation-Reduction
Nuclear Chemistry
Newton's Laws of Motion
Work and Energy Packet
Static Electricity Review
NGSS Alignments
1D-Kinematics
Projectiles
Circular Motion
Magnetism and Electromagnetism
Graphing Practice
About the ACT
ACT Preparation
For Teachers
Other Resources
Solutions Guide
Solutions Guide Digital Download
Motion in One Dimension
Work, Energy and Power
Chemistry of Matter
Measurement and the Metric System
Early Atomic Models
Names and Formulas
Algebra Based On-Level Physics
Honors Physics
Conceptual Physics
Other Tools
Frequently Asked Questions
Purchasing the Download
Purchasing the Digital Download
About the NGSS Corner
NGSS Search
Force and Motion DCIs - High School
Energy DCIs - High School
Wave Applications DCIs - High School
Force and Motion PEs - High School
Energy PEs - High School
Wave Applications PEs - High School
Crosscutting Concepts
The Practices
Physics Topics
NGSS Corner: Activity List
NGSS Corner: Infographics
About the Toolkits
Position-Velocity-Acceleration
Position-Time Graphs
Velocity-Time Graphs
Newton's First Law
Newton's Second Law
Newton's Third Law
Terminal Velocity
Projectile Motion
Forces in 2 Dimensions
Impulse and Momentum Change
Momentum Conservation
Work-Energy Fundamentals
Work-Energy Relationship
Roller Coaster Physics
Satellite Motion
Electric Fields
Circuit Concepts
Series Circuits
Parallel Circuits
Describing-Waves
Wave Behavior Toolkit
Standing Wave Patterns
Resonating Air Columns
Wave Model of Light
Plane Mirrors
Curved Mirrors
Teacher Guide
Using Lab Notebooks
Current Electricity
Light Waves and Color
Reflection and Ray Model of Light
Refraction and Ray Model of Light
Teacher Resources
Subscriptions

Newton's Laws
Einstein's Theory of Special Relativity
About Concept Checkers
School Pricing
Newton's Laws of Motion
Newton's First Law
Newton's Third Law

Mission KC6: Average Speed Computations

Mission KC6 pertains to the relationship between the distance traveled, the time of travel, and the average speed. Questions involve calculations. The mission consists of 14 questions organized into 7 Question Groups. You must answer one question from each Question Group to complete the mission. The learning outcomes for this mission are ...

Learning Outcomes

The student should be able to use the average speed equation to perform simple computations and solve word problems.

Launch Mission KC6

Getting help.

If you are not familiar with this topic, then you should first learn about the topic using our written Tutorial or our Video Tutorial: The Physics Classroom, One-Dimensional Kinematics Unit, Lesson 1, Part d

How can the average speed equation be used to solve problems involving distance, time and speed?

Video Tutorial: Speed vs. Velocity

Question-Specific Help

Each Question Group has its own Help page with information specific to the question. You can access the Help page from within the mission by tapping on the Help Me! icon (textbook). For your convenience, links to those pages are provided below: