explain alternative hypothesis

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Apr 16, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Module 9: Hypothesis Testing With One Sample

Null and alternative hypotheses, learning outcomes.

• Describe hypothesis testing in general and in practice

The actual test begins by considering two  hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make adecision. There are two options for a  decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in  H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40

• H 0 : p = 0.40
• H a : p > 0.40

Concept Review

In a  hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

H 0 and H a are contradictory.

• OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License

Alternative hypothesis

by Marco Taboga , PhD

In a statistical test, observed data is used to decide whether or not to reject a restriction on the data-generating probability distribution.

The assumption that the restriction is true is called null hypothesis , while the statement that the restriction is not true is called alternative hypothesis.

A correct specification of the alternative hypothesis is essential to decide between one-tailed and two-tailed tests.

Table of contents

Mathematical setting

Choice between one-tailed and two-tailed tests, the critical region, the interpretation of the rejection, the interpretation must be coherent with the alternative hypothesis.

• Power function

Accepting the alternative

More details, keep reading the glossary.

In order to fully understand the concept of alternative hypothesis, we need to remember the essential elements of a statistical inference problem:

we observe a sample drawn from an unknown probability distribution;

in principle, any valid probability distribution could have generated the sample;

however, we usually place some a priori restrictions on the set of possible data-generating distributions;

A couple of simple examples follow.

When we conduct a statistical test, we formulate a null hypothesis as a restriction on the statistical model.

The alternative hypothesis is

The alternative hypothesis is used to decide whether a test should be one-tailed or two-tailed.

The null hypothesis is rejected if the test statistic falls within a critical region that has been chosen by the statistician.

The critical region is a set of values that may comprise:

only the left tail of the distribution or only the right tail (one-tailed test);

both the left and the right tail (two-tailed test).

The choice of the critical region depends on the alternative hypothesis. Let us see why.

The interpretation is different depending on the tail of the distribution in which the test statistic falls.

The choice between a one-tailed or a two-tailed test needs to be done in such a way that the interpretation of a rejection is always coherent with the alternative hypothesis.

When we deal with the power function of a test, the term "alternative hypothesis" has a special meaning.

We conclude with a caveat about the interpretation of the outcome of a test of hypothesis.

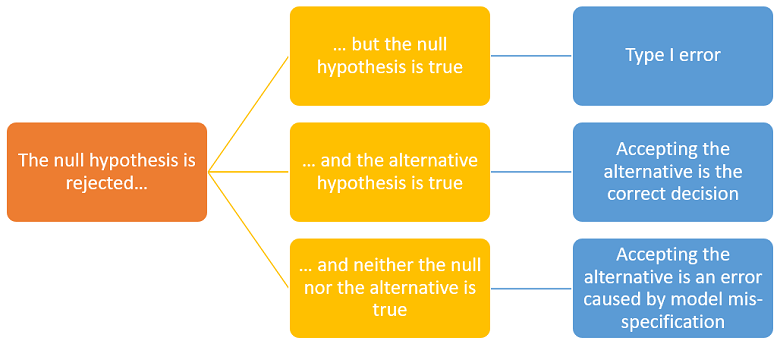
The interpretation of a rejection of the null is controversial.

According to some statisticians, rejecting the null is equivalent to accepting the alternative.

However, others deem that rejecting the null does not necessarily imply accepting the alternative. In fact, it is possible to think of situations in which both hypotheses can be rejected. Let us see why.

According to the conceptual framework illustrated by the images above, there are three possibilities:

the null is true;

the alternative is true;

neither the null nor the alternative is true because the true data-generating distribution has been excluded from the statistical model (we say that the model is mis-specified).

If we are in case 3, accepting the alternative after a rejection of the null is an incorrect decision. Moreover, a second test in which the alternative becomes the new null may lead us to another rejection.

You can find more details about the alternative hypothesis in the lecture on Hypothesis testing .

Previous entry: Almost sure

Next entry: Binomial coefficient

How to cite

Please cite as:

Taboga, Marco (2021). "Alternative hypothesis", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/alternative-hypothesis.

Most of the learning materials found on this website are now available in a traditional textbook format.

• Maximum likelihood
• Binomial distribution
• Beta distribution
• Convergence in probability
• Delta method
• Exponential distribution
• Chi-square distribution
• Set estimation
• Wishart distribution
• Mathematical tools
• Fundamentals of probability
• Probability distributions
• Asymptotic theory
• Fundamentals of statistics
• About Statlect
• Cookies, privacy and terms of use
• Precision matrix
• Loss function
• Integrable variable
• Critical value
• To enhance your privacy,
• we removed the social buttons,
• but don't forget to share .